【Leetcode】2045. 到达目的地的第二短时间

最新推荐文章于 2025-12-20 22:59:04 发布

转载最新推荐文章于 2025-12-20 22:59:04 发布 · 322 阅读

CC 4.0 BY-SA版权

原文链接：https://leetcode-cn.com/problems/second-minimum-time-to-reach-destination/solution/dao-da-mu-de-di-de-di-er-duan-shi-jian-b-05i0/

文章标签：

#leetcode #算法 #到达目的地的第二短时间 #广度优先搜索 #邻接表

LeetCode编程题笔记专栏收录该内容

63 篇文章

订阅专栏

本文介绍了一种利用广度优先搜索求解特定图上第二短时间路径的方法，并提供了一个具体的Python实现示例。

题目描述

城市用一个双向连通图表示，图中有 n 个节点，从 1 到 n 编号（包含 1 和 n）。图中的边用一个二维整数数组 edges 表示，其中每个 $edges[i] = [u_i, v_i]$ 表示一条节点 $u_i$ 和节点 $v_i$ 之间的双向连通边。每组节点对由 最多一条 边连通，顶点不存在连接到自身的边。穿过任意一条边的时间是 time 分钟。

每个节点都有一个交通信号灯，每 change 分钟改变一次，从绿色变成红色，再由红色变成绿色，循环往复。所有信号灯都 同时 改变。你可以在 任何时候 进入某个节点，但是 只能 在节点 信号灯是绿色时 才能离开。如果信号灯是 绿色 ，你 不能 在节点等待，必须离开。

第二小的值 是 严格大于 最小值的所有值中最小的值。

例如，[2, 3, 4] 中第二小的值是 3 ，而 [2, 2, 4] 中第二小的值是 4 。

给你 n、edges、time 和 change ，返回从节点 1 到节点 n 需要的 第二短时间。

注意：

你可以 任意次 穿过任意顶点，包括 1 和 n 。
你可以假设在 启程时 ，所有信号灯刚刚变成 绿色。

示例1
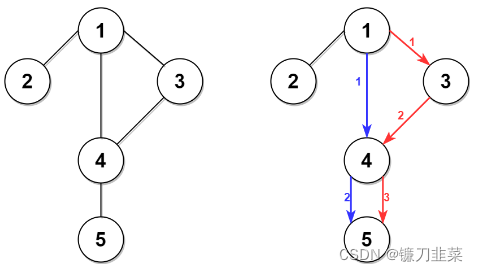
到达目的地的第二短时间

输入：n = 5, edges = [[1,2],[1,3],[1,4],[3,4],[4,5]], time = 3, change = 5
输出：13
解释：
上面的左图展现了给出的城市交通图。
右图中的蓝色路径是最短时间路径。
花费的时间是：
- 从节点 1 开始，总花费时间=0
- 1 -> 4：3 分钟，总花费时间=3
- 4 -> 5：3 分钟，总花费时间=6
因此需要的最小时间是 6 分钟。

右图中的红色路径是第二短时间路径。
- 从节点 1 开始，总花费时间=0
- 1 -> 3：3 分钟，总花费时间=3
- 3 -> 4：3 分钟，总花费时间=6
- 在节点 4 等待 4 分钟，总花费时间=10
- 4 -> 5：3 分钟，总花费时间=13
因此第二短时间是 13 分钟。

示例2
到达目的地的第二短时间

输入：n = 2, edges = [[1,2]], time = 3, change = 2
输出：11
解释：
最短时间路径是 1 -> 2 ，总花费时间 = 3 分钟
最短时间路径是 1 -> 2 -> 1 -> 2 ，总花费时间 = 11 分钟

提示

$2 <= n <= 10^4$
$n - 1 <= edges.length <= min(2 * 10^4, n * (n - 1) / 2)$
$e d g e s [i] . l e n g t h = = 2$
$1 <= u_i, v_i <= n$
$u_i != v_i$
不含重复边
每个节点都可以从其他节点直接或者间接到达
$1 <= time, change <= 10^3$

解题思路

根据题意可知，同一路径长度所需花费的时间是相同的，且路径越长，所需时间越久。因此，可以求得到达目的地的严格次短路径，就可以直接计算到达目的地的第二短时间。

求解权重相同的最短路径问题可以采用广度优先搜索，但是这里做一些修改。使用广度优先搜索求解最短路径时，经过的点与初始点的路径长度是所有未搜索过的路径中的最小值，因此每次广度优先搜索获得的经过点与初始点的路径长度是非递减的。可以记录下所有点与初始点的最短路径与严格次短路径，一旦求得目标点与严格次短路径，就可以直接计算到达目的地的第二短路径。

对于路径长度与实践的计算，假设到达节点i的时间为 $t_i$ ，则到达节点 $i + 1$ 的时间为：
$t_{i+1}=t_i+t_{wait}+time$
其中， $t_{wait}$ 的计算如下：
$t_{wait}=\begin{cases} 0 & \text { if } {t_i\mod{2\times change}\in [0,change)}\\ 2\times change-t_i\mod{2\times change} & \text{ if }t_i \mod{2\times change}\in [change, 2 \times change) \end{cases}$

代码展示

#!/usr/bin/env python
# -*- coding:utf-8 -*-
# @FileName  :SecondMinimum.py
# @Time      :2022/1/25 19:34
# @Author    :PangXZ
# Leetcode 2045:到达目的地的第二短时间
from collections import deque
from typing import List


class Solution:
    def secondMinimum(self, n: int, edges: List[List[int]], time: int, change: int) -> int:
        graph = [[] for _ in range(n + 1)]  # 创建一个二维数组存储从每个节点出发的目的地
        for e in edges:
            x, y = e[0], e[1]
            graph[x].append(y)
            graph[y].append(x)

        # dist[i][0]表示从1到i的最短路径，dist[i][1]表示从1到i的严格次短路径
        dist = [[float('inf')] * 2 for _ in range(n + 1)]
        dist[1][0] = 0  # 表示 从1出发到它本身的最短路径为1
        q = deque([(1, 0)])  # 广度优先搜索队列，从1出发，步长为0
        while dist[n][1] == float('inf'):  # 表示从1到n的严格次短路径为无限大时，执行循环
            p = q.popleft()
            for y in graph[p[0]]:  # 遍历当前节点的所有可到达节点
                d = p[1] + 1  # 表示步长
                if d < dist[y][0]:  # 如果d小于当前到y的最短路径, 体现广度优先搜索
                    dist[y][0] = d  # 更新最短路径
                    q.append((y, d))
                elif dist[y][0] < d < dist[y][1]:  # 如果d大于当前到y的最短路径，小于到y的严格次短路径
                    dist[y][1] = d  # 更新严格次短路径
                    q.append((y, d))
        ans = 0
        for _ in range(int(dist[n][1])):  # 模拟从1开始到n的严格次短路径上的过程
            if ans % (change * 2) >= change:   # 如果当前超过达到信号灯变化的时刻， 则需要加上等待时间
                ans += change * 2 - ans % (change * 2)
            ans += time  # 加上通过时间
        return ans


if __name__ == "__main__":
    solution = Solution()
    print(solution.secondMinimum(n=5, edges=[[1, 2], [1, 3], [1, 4], [3, 4], [4, 5]], time=3, change=5))