PRML笔记：1-介绍

打算去读PRML这本书，用两遍来读完，第一遍弄懂基本思想，以便看其他任何相关文献能够明白他们在说什么；第二遍细看，重点要做书后面的习题，弄清每个知识点的细节部分。第二遍可能不会连续，甚至会挑选部分章节重点研究，但是第一遍需要坚持。近期的博文就是记录自己看到的关键知识概念，到时碰到不懂的时候，再去google查找进一步的解析。行文都依照原作者书中介绍的顺序，希望这些概念能够将整体知识串接起来……

------------------分割线----------------------

训练集（training set）：用来训练模型的观察数据{  }，有的时候会带上目标向量；

训练（training）或者学习（learning）：寻找一个最优函数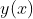，使其能够与尽可能接近。

有时需要对数据进行预处理（preprocessed），比如一幅图像有很多像素点组成，我们不需要将这些数据全部输入模型，而是先进行一个特征提取的工作（feature extraction），这是计算机视觉领域一个很重要的工作。同样，新的需要被预测的数据也要进行同样的预处理工作。

当训练好一个模型后，这个模型预测新的数据的能力就称为生成能力（generalization），当为离散值的时候，称为分类问题（classification），如果是连续值，就是回归问题（regression）。在训练学习过程中，有值就称为监督学习（supervised learning），如果没有就是非监督学习（unsupervised learning），前面提到的分类、回归问题就属于监督学习范畴，非监督学习包括聚类（clustering）、数据概率分布估计（density estimation）等。

增强学习（reinforcement learning）大概就是在学习阶段去发现一些误差，当前采取的措施需要经过若干步的认证（这个没有弄明白，后续再来解释吧）

在机器学习、模式识别中，需要应用到概率论、决策论、信息论的知识。

实例：多项式拟合

假设目前有N个训练数据 和相应的观察值，这些数据其实是函数生成的，我们的目的就是用多项式拟合去逼近这个真实函数。所以假设我们的多项式为

那么我们需要确定合适的系数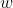来使近似于，一个直观想法就是建立一个误差标准

找到是这个误差函数最小的系数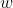，就确定了多项式的形式，也就确定好了模型。

事实上，多项式的阶数M需要我们多次试验去选择一个最合适的，次数太小，拟合不精确，次数太大，会造成过拟合。次数太小，很显然在训练阶段和测试阶段的误差都会很大，而过拟合却是一个别样的现象：在训练数据中的误差会很小，如果次数足够大，甚至为0（这个很容易想象，只要次数大于训练数据数目），但是在测试数据集中，误差会变的相当大，而且系数会变得很大。

解决过拟合有两种方案：

1、在次数不变的情况下，增多训练数据；

2、引入正则项（regularization term）约束系数，所以误差函数（1）可以改成如下：

正则项的引入可以保证系数不至于太大（太大会增大误差）。

概率观点：

用概率模型来解释多项式拟合的问题，一个假设是数据是独立同分布的高斯分布，那么我们的目的就是保证学到的模型，是最可能生成观察数据的，这就是似然思想，观察到某个结果，只找最可能的原因。似然函数如下：

一般采取对数形式：

先不讨论。

令似然函数最大，先求导，

这个和（1）的形式相同。

按照贝叶斯公式，需要结合先验概率和似然函数来估计后验概率，即

而也是一个高斯分布，即

所以有了最大化后验概率（maximum posterior，MAP），同样使其最大化，需要最小化以下导数：

这个和（2）式形式相同。

所以最大化似然函数对应于一般的最小二乘法，而最大化后验概率对应于正则化的二乘。

注意：

1）在实际模型选择中，为了充分利用已有的数据，需要将数据分为训练集、验证集、测试集，交叉多次使用。

2）维数灾难（curse of dimensionality）

决策观点：

一般在做决策时，只要使平均误差最小化就行，但是，有的时候误差种类的代价是不同的，这个时候模型就要偏向于代价小的方向，这个就是最小化代价方案。需要建立一个代价函数（cost function 或 loss function），有的时候采取最大化功效函数（utility function）的方式。

主要有两种类型的模型：生成模型（generative model）和判别模型（discriminative model），前者比后者复杂一些。

信息论观点：

主要利用熵（entropy）来衡量信息的大小，熵的公式：

其中有一个交叉熵或者相对熵（relative entropy，KL divergence）的概念，用来衡量两个随机变量的概率分布的接近程度，公式如下：

交叉熵是不对称的，概率越接近，值越小。