6.查找算法

一、线性查找

代码实现

public class SeqSearch {
    public static void main(String[] args) {
        int arr[] = { 1, 9, 11, -1, 34, 89 };
    }

    public static int seqSearch(int[] arr, int value) {
        for (int i = 0; i < arr.length; i++) {
            if (arr[i] == value) {
                return i;
            }
        }
        return -1;
    }
}

二、二分查找

1.思路分析

2.代码实现

public class BinarySearch {
    public static void main(String[] args) {
        int arr[] = { 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 , 11, 12, 13,14,15,16,17,18,19,20 };
        System.out.println(binarySearch(arr,0,arr.length-1,22));
    }

    public static int binarySearch(int[] arr, int left, int right, int findValue) {
        if (left > right) {
            return -1;
        }

        int mid = (left + right) / 2;
        int midVal = arr[mid];

        if (findValue > midVal) {
            return binarySearch(arr, mid + 1, right, findValue);
        } else if (findValue < midVal) {
            return binarySearch(arr, left, mid - 1, findValue);
        } else {
            return mid;
        }
    }
}

三、插值查找

1.思路分析

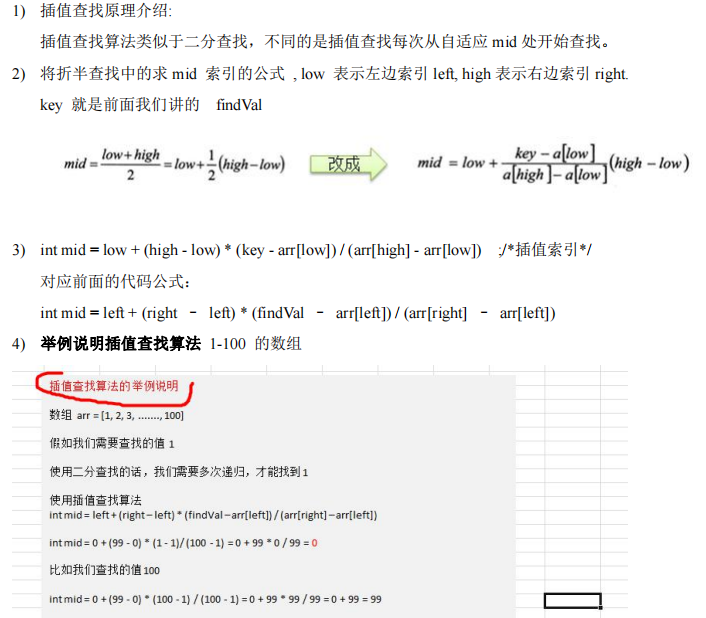
2.代码实现

public class InsertValueSearch {
    public static void main(String[] args) {

		int [] arr = new int[100];
		for(int i = 0; i < 100; i++) {
			arr[i] = i + 1;
		}

        int index = insertValueSearch(arr, 0, arr.length - 1, 1234);
        System.out.println("index = " + index);
    }

    public static int insertValueSearch(int[] arr, int left, int right, int findVal) {
        if (left > right || findVal < arr[0] || findVal > arr[arr.length - 1]) {
            return -1;
        }
        int mid = left + (right - left) * (findVal - arr[left]) / (arr[right] - arr[left]);
        int midVal = arr[mid];
        if (findVal > midVal) {
            return insertValueSearch(arr, mid + 1, right, findVal);
        } else if (findVal < midVal) {
            return insertValueSearch(arr, left, mid - 1, findVal);
        } else {
            return mid;
        }
    }
}

四、斐波那契（黄金分割法）查找算法

1.思路分析

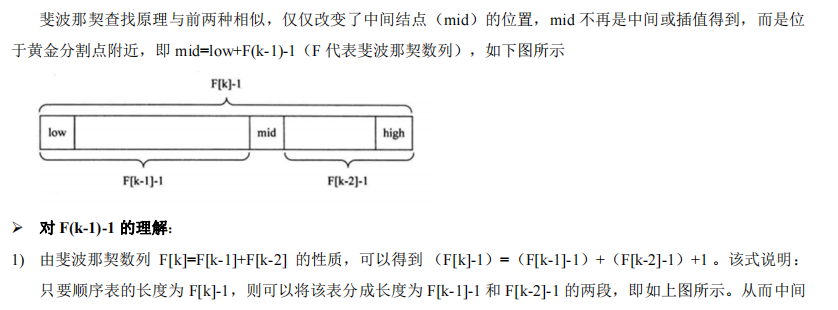
2.代码实现

public class FibonacciSearch {
    public static int maxSize = 20;
    public static void main(String[] args) {
        int [] arr = {1,8, 10, 89, 1000, 1234};
        System.out.println("index=" + fibSearch(arr, 189));// 0
    }

    public static int[] fib() {
        int[] f = new int[maxSize];
        f[0] = 1;
        f[1] = 1;
        for (int i = 2; i < maxSize; i++) {
            f[i] = f[i - 1] + f[i - 2];
        }
        return f;
    }

    public static int fibSearch(int[] a, int key) {
        int low = 0;
        int high = a.length - 1;
        int k = 0;
        int mid = 0;
        int f[] = fib();
        while(high > f[k] - 1) {
            k++;
        }
        int[] temp = Arrays.copyOf(a, f[k]);
        for(int i = high + 1; i < temp.length; i++) {
            temp[i] = a[high];
        }
        while (low <= high) {
            mid = low + f[k - 1] - 1;
            if(key < temp[mid]) {
                high = mid - 1;
                k--;
            } else if ( key > temp[mid]) {
                low = mid + 1;
                k -= 2;
            } else {
                if(mid <= high) {
                    return mid;
                } else {
                    return high;
                }
            }
        }
        return -1;
    }
}

return mid;
} else {
return high;
}
}
}
return -1;
}
}