8.树及其应用

一、介绍

1.优点

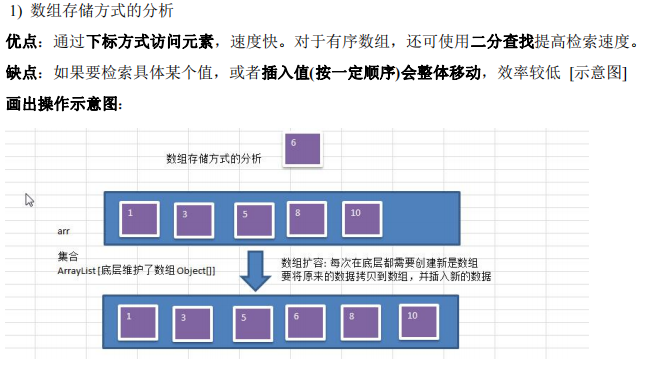
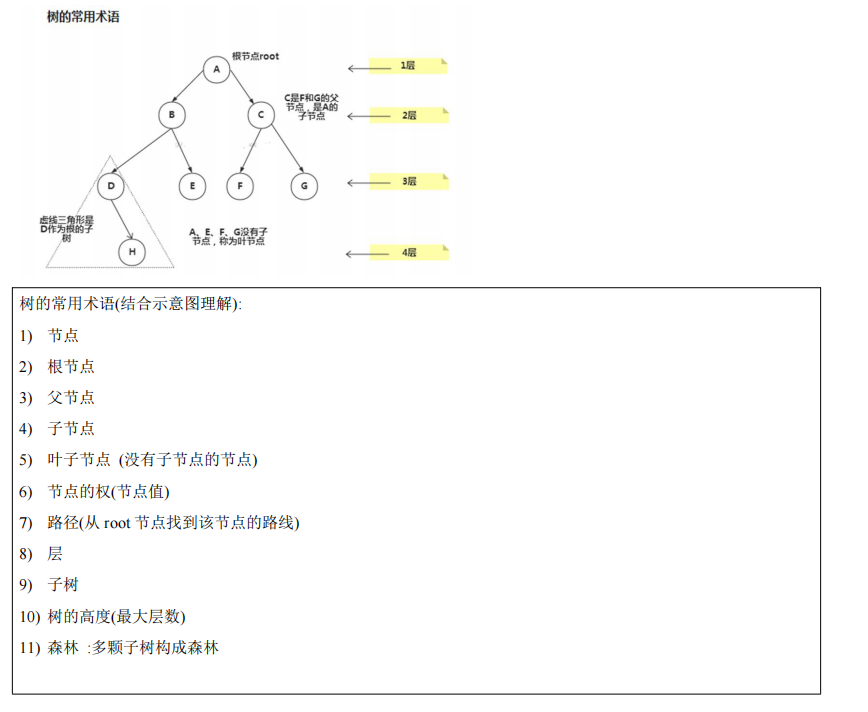
2.常用术语

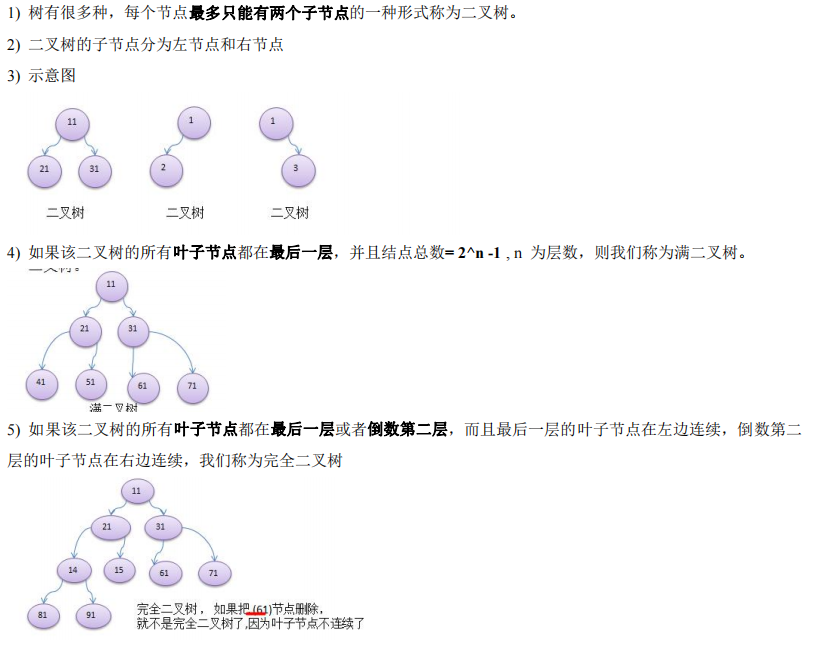
二、二叉树

1.概念

2.遍历

思路分析

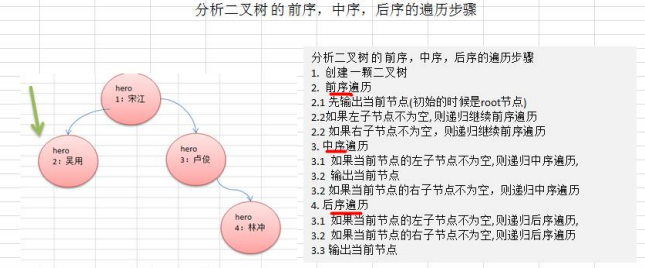
代码实现

public class BinaryTreeDemo {
    public static void main(String[] args) {

    }
}

class BinaryTree {
    private HeroNode root;

    public void setRoot(HeroNode root) {
        this.root = root;
    }

    public void preOrer() {
        if (this.root != null) {
            this.root.preOrder();
        } else {
            System.out.println("null");
        }
    }

    public void infixOrder() {
        if (this.root != null) {
            this.root.infixOrder();
        } else {
            System.out.println("null");
        }
    }

    public void postOrder() {
        if (this.root != null) {
            this.root.postOrder();
        } else {
            System.out.println("null");
        }
    }
}

class HeroNode {
    private int no;
    private String name;
    private HeroNode left;
    private HeroNode right;

    public HeroNode(int no, String name) {
        this.no = no;
        this.name = name;
    }

    public int getNo() {
        return no;
    }

    public void setNo(int no) {
        this.no = no;
    }

    public String getName() {
        return name;
    }

    public void setName(String name) {
        this.name = name;
    }

    public HeroNode getLeft() {
        return left;
    }

    public void setLeft(HeroNode left) {
        this.left = left;
    }

    public HeroNode getRight() {
        return right;
    }

    public void setRight(HeroNode right) {
        this.right = right;
    }

    @Override
    public String toString() {
        return "HeroNode{" +
                "no=" + no +
                ", name='" + name + '\'' +
                '}';
    }

    public void preOrder() {
        System.out.println(this);
        if (this.left != null) {
            this.left.preOrder();
        }
        if (this.right != null) {
            this.right.preOrder();
        }
    }

    public void infixOrder() {
        if (this.left != null) {
            this.left.infixOrder();
        }
        System.out.println(this);
        if (this.right != null) {
            this.right.infixOrder();
        }
    }

    public void postOrder() {
        if (this.left != null) {
            this.left.postOrder();
        }
        if (this.right != null) {
            this.right.postOrder();
        }
        System.out.println(this);
    }
}

3.顺序存储二叉树

（1）基本介绍

（2）特点

（3）代码实现

public class ArrBinaryTreeDemo {
    public static void main(String[] args) {
        int[] arr = { 1, 2, 3, 4, 5, 6, 7 };
        ArrBinaryTree arrBinaryTree = new ArrBinaryTree(arr);
        arrBinaryTree.preOrder();
    }
}

class ArrBinaryTree {
    private int[] arr;

    public ArrBinaryTree(int[] arr) {
        this.arr = arr;
    }

    public void preOrder() {
        this.preOrder(0);
    }

    public void preOrder(int index) {
        if(arr == null || arr.length == 0) {
            System.out.println("empty");
        }
        System.out.println(arr[index]);
        if((index * 2 + 1) < arr.length) {
            preOrder(2 * index + 1 );
        }
        if((index * 2 + 2) < arr.length) {
            preOrder(2 * index + 2);
        }
    }

}

4.线索化二叉树

（1）介绍

（2）中序遍历思路分析

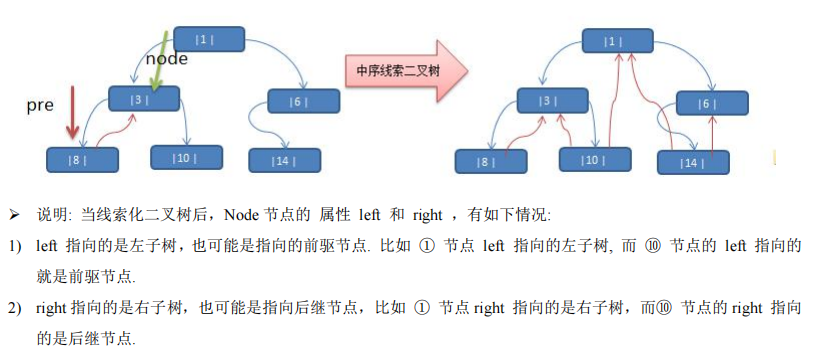
（3）代码实现

public class ThreadedBinaryTreeDemo {
    public static void main(String[] args) {
        HeroNode root = new HeroNode(1, "tom");
        HeroNode node2 = new HeroNode(3, "jack");
        HeroNode node3 = new HeroNode(6, "smith");
        HeroNode node4 = new HeroNode(8, "mary");
        HeroNode node5 = new HeroNode(10, "king");
        HeroNode node6 = new HeroNode(14, "dim");

        root.setLeft(node2);
        root.setRight(node3);
        node2.setLeft(node4);
        node2.setRight(node5);
        node3.setLeft(node6);

        ThreadedBinaryTree threadedBinaryTree = new ThreadedBinaryTree();
        threadedBinaryTree.setRoot(root);
        threadedBinaryTree.threadedNodes();

        HeroNode leftNode = node5.getLeft();
        HeroNode rightNode = node5.getRight();
        System.out.println("10号结点的前驱结点是 ="  + leftNode); //3
        System.out.println("10号结点的后继结点是="  + rightNode); //1

        //threadedBinaryTree.infixOrder();
        System.out.println("使用线索化的方式遍历 线索化二叉树");
        threadedBinaryTree.threadedList(); // 8, 3, 10, 1, 14, 6
    }
}

class ThreadedBinaryTree {
    private HeroNode root;
    private HeroNode pre = null;

    public void setRoot(HeroNode root) {
        this.root = root;
    }
    public void threadedNodes() {
        this.threadedNodes(root);
    }

    public void threadedList() {
        HeroNode node = root;
        while(node != null) {
            while(node.getLeftType() == 0) {
                node = node.getLeft();
            }

            System.out.println(node);
            while(node.getRightType() == 1) {
                node = node.getRight();
                System.out.println(node);
            }
            node = node.getRight();
        }
    }
    public void threadedNodes(HeroNode node) {
        if(node == null) {
            return;
        }
        threadedNodes(node.getLeft());
        if(node.getLeft() == null) {
            node.setLeft(pre);
            node.setLeftType(1);
        }

        if (pre != null && pre.getRight() == null) {
            pre.setRight(node);
            pre.setRightType(1);
        }
        pre = node;
        threadedNodes(node.getRight());
    }

    public void delNode(int no) {
        if(root != null) {
            if(root.getNo() == no) {
                root = null;
            } else {
                root.delNode(no);
            }
        }else{
            System.out.println("空树，不能删除~");
        }
    }
    public void preOrder() {
        if(this.root != null) {
            this.root.preOrder();
        }else {
            System.out.println("二叉树为空，无法遍历");
        }
    }
    public void infixOrder() {
        if(this.root != null) {
            this.root.infixOrder();
        }else {
            System.out.println("二叉树为空，无法遍历");
        }
    }
    public void postOrder() {
        if(this.root != null) {
            this.root.postOrder();
        }else {
            System.out.println("二叉树为空，无法遍历");
        }
    }
    public HeroNode preOrderSearch(int no) {
        if(root != null) {
            return root.preOrderSearch(no);
        } else {
            return null;
        }
    }
    public HeroNode infixOrderSearch(int no) {
        if(root != null) {
            return root.infixOrderSearch(no);
        }else {
            return null;
        }
    }
    public HeroNode postOrderSearch(int no) {
        if(root != null) {
            return this.root.postOrderSearch(no);
        }else {
            return null;
        }
    }
}

class HeroNode {
    private int no;
    private String name;
    private HeroNode left; //默认null
    private HeroNode right; //默认null
    private int leftType;
    private int rightType;

    public int getLeftType() {
        return leftType;
    }
    public void setLeftType(int leftType) {
        this.leftType = leftType;
    }
    public int getRightType() {
        return rightType;
    }
    public void setRightType(int rightType) {
        this.rightType = rightType;
    }
    public HeroNode(int no, String name) {
        this.no = no;
        this.name = name;
    }
    public int getNo() {
        return no;
    }
    public void setNo(int no) {
        this.no = no;
    }
    public String getName() {
        return name;
    }
    public void setName(String name) {
        this.name = name;
    }
    public HeroNode getLeft() {
        return left;
    }
    public void setLeft(HeroNode left) {
        this.left = left;
    }
    public HeroNode getRight() {
        return right;
    }
    public void setRight(HeroNode right) {
        this.right = right;
    }
    @Override
    public String toString() {
        return "HeroNode [no=" + no + ", name=" + name + "]";
    }

    public void delNode(int no) {
        if(this.left != null && this.left.no == no) {
            this.left = null;
            return;
        }
        if(this.right != null && this.right.no == no) {
            this.right = null;
            return;
        }
        if(this.left != null) {
            this.left.delNode(no);
        }
        if(this.right != null) {
            this.right.delNode(no);
        }
    }

    public void preOrder() {
        System.out.println(this);
        if(this.left != null) {
            this.left.preOrder();
        }
        if(this.right != null) {
            this.right.preOrder();
        }
    }
    public void infixOrder() {
        if(this.left != null) {
            this.left.infixOrder();
        }
        System.out.println(this);
        if(this.right != null) {
            this.right.infixOrder();
        }
    }
    public void postOrder() {
        if(this.left != null) {
            this.left.postOrder();
        }
        if(this.right != null) {
            this.right.postOrder();
        }
        System.out.println(this);
    }
    public HeroNode preOrderSearch(int no) {
        System.out.println("进入前序遍历");
        if(this.no == no) {
            return this;
        }
        HeroNode resNode = null;
        if(this.left != null) {
            resNode = this.left.preOrderSearch(no);
        }
        if(resNode != null) {
            return resNode;
        }
        if(this.right != null) {
            resNode = this.right.preOrderSearch(no);
        }
        return resNode;
    }
    public HeroNode infixOrderSearch(int no) {
        HeroNode resNode = null;
        if(this.left != null) {
            resNode = this.left.infixOrderSearch(no);
        }
        if(resNode != null) {
            return resNode;
        }
        System.out.println("进入中序查找");
        if(this.no == no) {
            return this;
        }
        if(this.right != null) {
            resNode = this.right.infixOrderSearch(no);
        }
        return resNode;

    }
    public HeroNode postOrderSearch(int no) {
        HeroNode resNode = null;
        if(this.left != null) {
            resNode = this.left.postOrderSearch(no);
        }
        if(resNode != null) {
            return resNode;
        }
        if(this.right != null) {
            resNode = this.right.postOrderSearch(no);
        }
        if(resNode != null) {
            return resNode;
        }
        System.out.println("进入后序查找");
        if(this.no == no) {
            return this;
        }
        return resNode;
    }
}

三、堆排序

1.介绍

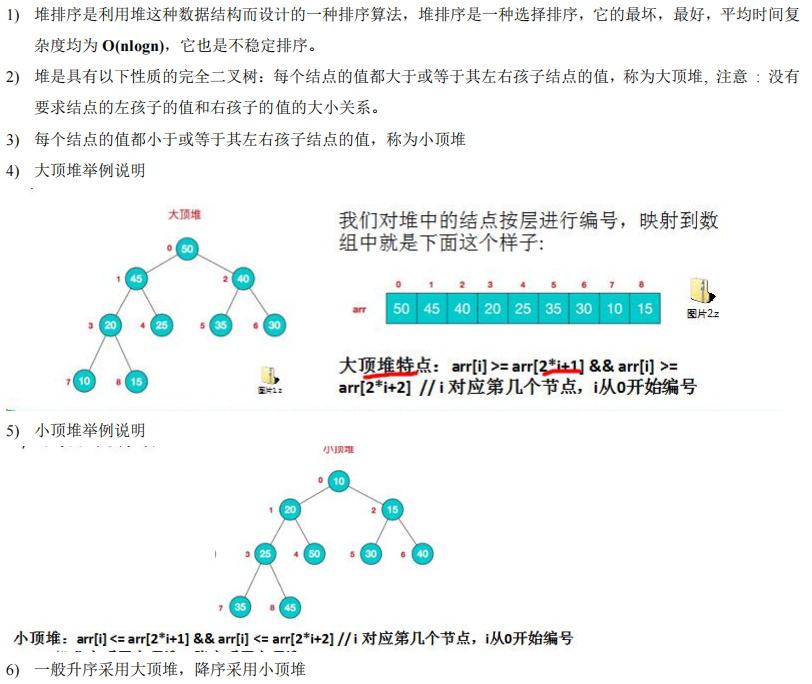
2.基本思想

3.步骤图解

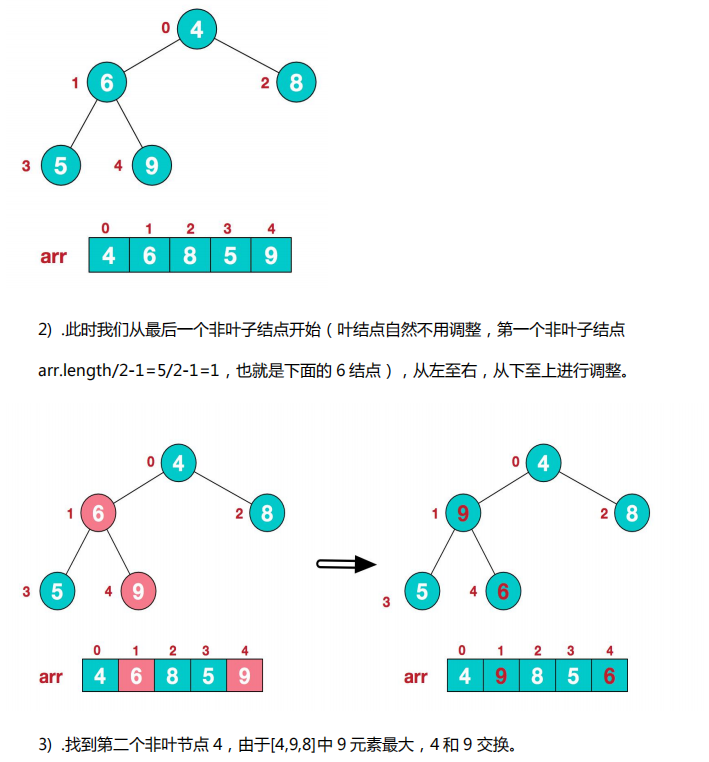
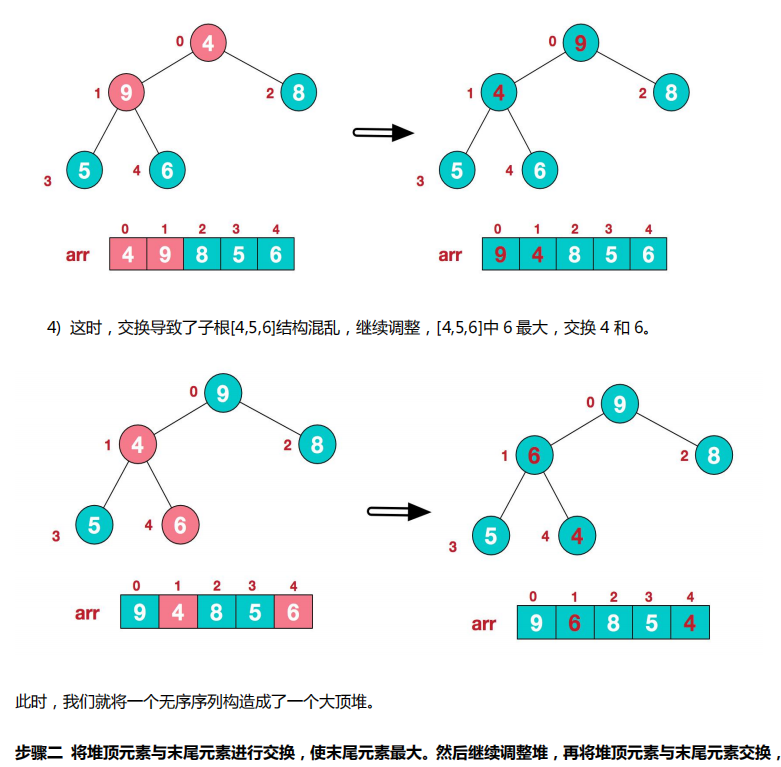
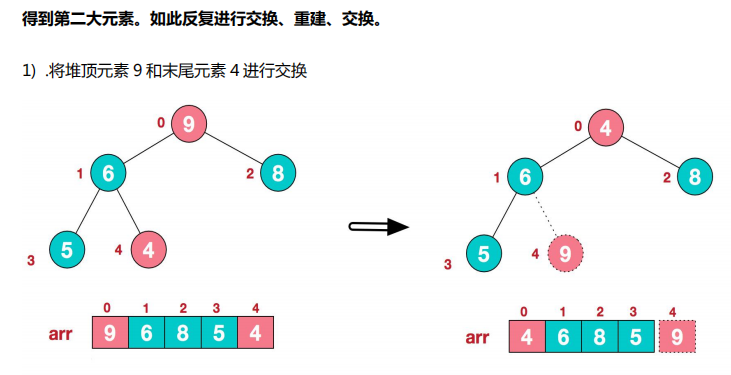
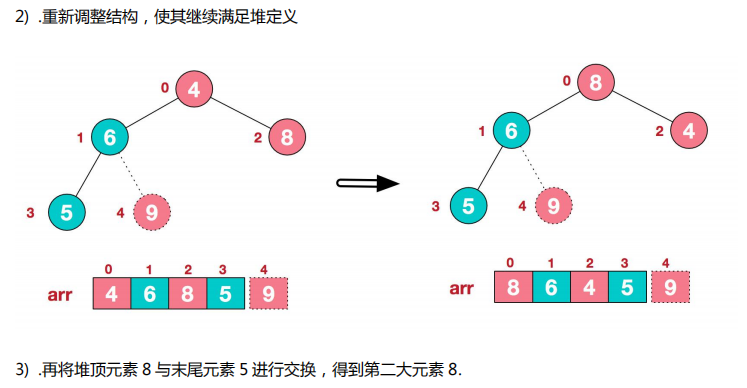
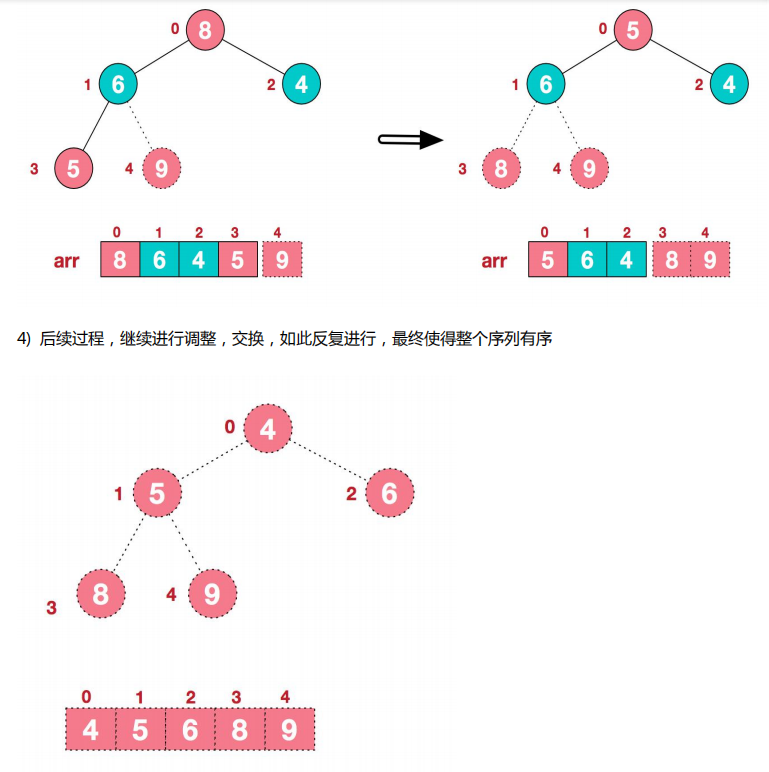
4.代码实现

public class HeapSort {

	public static void main(String[] args) {
		//要求将数组进行升序排序
		//int arr[] = {4, 6, 8, 5, 9};
		// 创建要给80000个的随机的数组
		int[] arr = new int[8000000];
		for (int i = 0; i < 8000000; i++) {
			arr[i] = (int) (Math.random() * 8000000); // 生成一个[0, 8000000) 数
		}

		System.out.println("排序前");
		Date data1 = new Date();
		SimpleDateFormat simpleDateFormat = new SimpleDateFormat("yyyy-MM-dd HH:mm:ss");
		String date1Str = simpleDateFormat.format(data1);
		System.out.println("排序前的时间是=" + date1Str);
		
		heapSort(arr);
		
		Date data2 = new Date();
		String date2Str = simpleDateFormat.format(data2);
		System.out.println("排序前的时间是=" + date2Str);
		//System.out.println("排序后=" + Arrays.toString(arr));
	}

	//编写一个堆排序的方法
	public static void heapSort(int arr[]) {
		int temp = 0;
		System.out.println("堆排序!!");
		
//		//分步完成
//		adjustHeap(arr, 1, arr.length);
//		System.out.println("第一次" + Arrays.toString(arr)); // 4, 9, 8, 5, 6
//		
//		adjustHeap(arr, 0, arr.length);
//		System.out.println("第2次" + Arrays.toString(arr)); // 9,6,8,5,4
		
		//完成我们最终代码
		//将无序序列构建成一个堆，根据升序降序需求选择大顶堆或小顶堆
		for(int i = arr.length / 2 -1; i >=0; i--) {
			adjustHeap(arr, i, arr.length);
		}
		
		/*
		 * 2).将堆顶元素与末尾元素交换，将最大元素"沉"到数组末端;
　　			3).重新调整结构，使其满足堆定义，然后继续交换堆顶元素与当前末尾元素，反复执行调整+交换步骤，直到整个序列有序。
		 */
		for(int j = arr.length-1;j >0; j--) {
			//交换
			temp = arr[j];
			arr[j] = arr[0];
			arr[0] = temp;
			adjustHeap(arr, 0, j); 
		}
		
		//System.out.println("数组=" + Arrays.toString(arr)); 
		
	}
	
	//将一个数组(二叉树), 调整成一个大顶堆
	/**
	 * 功能： 完成 将 以 i 对应的非叶子结点的树调整成大顶堆
	 * 举例  int arr[] = {4, 6, 8, 5, 9}; => i = 1 => adjustHeap => 得到 {4, 9, 8, 5, 6}
	 * 如果我们再次调用  adjustHeap 传入的是 i = 0 => 得到 {4, 9, 8, 5, 6} => {9,6,8,5, 4}
	 * @param arr 待调整的数组
	 * @param i 表示非叶子结点在数组中索引
	 * @param lenght 表示对多少个元素继续调整， length 是在逐渐的减少
	 */
	public  static void adjustHeap(int arr[], int i, int lenght) {
		
		int temp = arr[i];//先取出当前元素的值，保存在临时变量
		//开始调整
		//说明
		//1. k = i * 2 + 1 k 是 i结点的左子结点
		for(int k = i * 2 + 1; k < lenght; k = k * 2 + 1) {
			if(k+1 < lenght && arr[k] < arr[k+1]) { //说明左子结点的值小于右子结点的值
				k++; // k 指向右子结点
			}
			if(arr[k] > temp) { //如果子结点大于父结点
				arr[i] = arr[k]; //把较大的值赋给当前结点
				i = k; //!!! i 指向 k,继续循环比较
			} else {
				break;//!
			}
		}
		//当for 循环结束后，我们已经将以i 为父结点的树的最大值，放在了 最顶(局部)
		arr[i] = temp;//将temp值放到调整后的位置
	}
	
}

四、赫夫曼树

1.介绍

2.重要概念

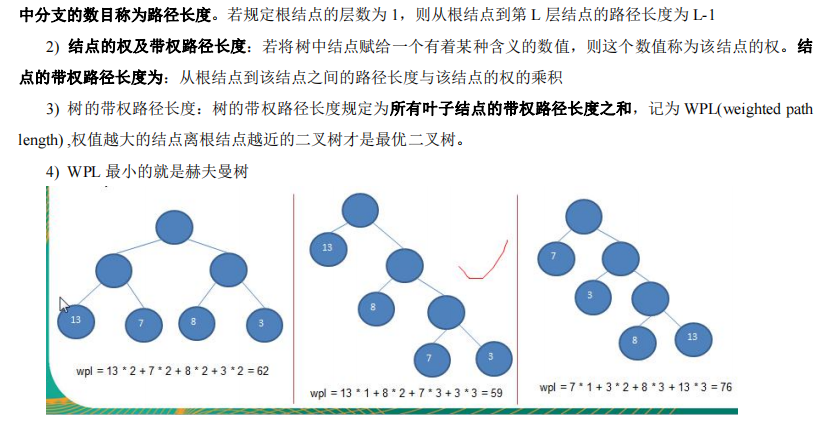
3.创建思路

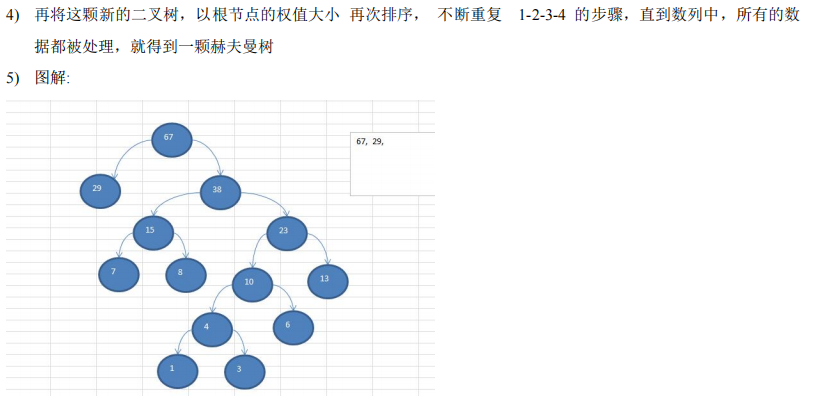
4.代码实现

public class HuffmanTree {
    public static void main(String[] args) {
        int arr[] = { 13, 7, 8, 3, 29, 6, 1 };
        Node root = create(arr);
        preOrder(root); //
    }

    public static void preOrder(Node root) {
        if (root != null) {
            root.preOrder();
        } else {
            System.out.println("empty");
        }
    }

    public static Node create(int[] arr) {
        List<Node> nodes = new ArrayList<Node>();
        for (int value : arr) {
            nodes.add(new Node(value));
        }

        while (nodes.size() > 1) {
            Collections.sort(nodes);
            Node left = nodes.get(0);
            Node right = nodes.get(1);
            Node parent = new Node(left.value + right.value);
            parent.left = left;
            parent.right = right;
            nodes.remove(right);
            nodes.remove(left);
            nodes.add(parent);
        }
        return nodes.get(0);
    }
}


class Node implements Comparable<Node>{
    int value;
    Node left;
    Node right;

    public Node(int value) {
        this.value = value;
    }

    @Override
    public String toString() {
        return "Node{" +
                "value=" + value +
                '}';
    }

    @Override
    public int compareTo(Node o) {
        return this.value - o.value;
    }

    public void preOrder() {
        System.out.println(this);
        if (this.left != null) {
            this.left.preOrder();
        }
        if (this.right != null) {
            this.right.preOrder();
        }
    }
}

五、赫夫曼编码

1.基本介绍

2.原理剖析

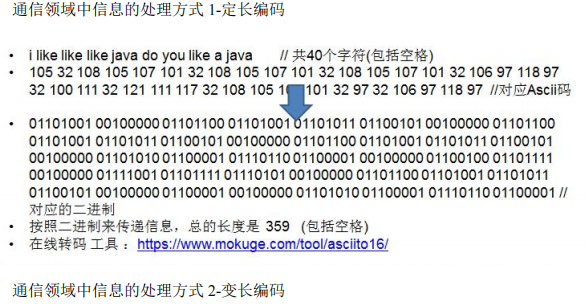
3.代码实现

public class HuffmanCode {

	public static void main(String[] args) {
		
		//测试压缩文件
//		String srcFile = "d://Uninstall.xml";
//		String dstFile = "d://Uninstall.zip";
//		
//		zipFile(srcFile, dstFile);
//		System.out.println("压缩文件ok~~");
		
		
		//测试解压文件
		String zipFile = "d://Uninstall.zip";
		String dstFile = "d://Uninstall2.xml";
		unZipFile(zipFile, dstFile);
		System.out.println("解压成功!");
		
		/*
		String content = "i like like like java do you like a java";
		byte[] contentBytes = content.getBytes();
		System.out.println(contentBytes.length); //40
		
		byte[] huffmanCodesBytes= huffmanZip(contentBytes);
		System.out.println("压缩后的结果是:" + Arrays.toString(huffmanCodesBytes) + " 长度= " + huffmanCodesBytes.length);
		
		
		//测试一把byteToBitString方法
		//System.out.println(byteToBitString((byte)1));
		byte[] sourceBytes = decode(huffmanCodes, huffmanCodesBytes);
		
		System.out.println("原来的字符串=" + new String(sourceBytes)); // "i like like like java do you like a java"
		*/
		
		
		
		//如何将 数据进行解压(解码)  
		//分步过程
		/*
		List<Node> nodes = getNodes(contentBytes);
		System.out.println("nodes=" + nodes);
		
		//测试一把，创建的赫夫曼树
		System.out.println("赫夫曼树");
		Node huffmanTreeRoot = createHuffmanTree(nodes);
		System.out.println("前序遍历");
		huffmanTreeRoot.preOrder();
		
		//测试一把是否生成了对应的赫夫曼编码
		Map<Byte, String> huffmanCodes = getCodes(huffmanTreeRoot);
		System.out.println("~生成的赫夫曼编码表= " + huffmanCodes);
		
		//测试
		byte[] huffmanCodeBytes = zip(contentBytes, huffmanCodes);
		System.out.println("huffmanCodeBytes=" + Arrays.toString(huffmanCodeBytes));//17
		
		//发送huffmanCodeBytes 数组 */
		
		
	}
	
	//编写一个方法，完成对压缩文件的解压
	/**
	 * 
	 * @param zipFile 准备解压的文件
	 * @param dstFile 将文件解压到哪个路径
	 */
	public static void unZipFile(String zipFile, String dstFile) {
		
		//定义文件输入流
		InputStream is = null;
		//定义一个对象输入流
		ObjectInputStream ois = null;
		//定义文件的输出流
		OutputStream os = null;
		try {
			//创建文件输入流
			is = new FileInputStream(zipFile);
			//创建一个和  is关联的对象输入流
			ois = new ObjectInputStream(is);
			//读取byte数组  huffmanBytes
			byte[] huffmanBytes = (byte[])ois.readObject();
			//读取赫夫曼编码表
			Map<Byte,String> huffmanCodes = (Map<Byte,String>)ois.readObject();
			
			//解码
			byte[] bytes = decode(huffmanCodes, huffmanBytes);
			//将bytes 数组写入到目标文件
			os = new FileOutputStream(dstFile);
			//写数据到 dstFile 文件
			os.write(bytes);
		} catch (Exception e) {
			// TODO: handle exception
			System.out.println(e.getMessage());
		} finally {
			
			try {
				os.close();
				ois.close();
				is.close();
			} catch (Exception e2) {
				// TODO: handle exception
				System.out.println(e2.getMessage());
			}
			
		}
	}
	
	//编写方法，将一个文件进行压缩
	/**
	 * 
	 * @param srcFile 你传入的希望压缩的文件的全路径
	 * @param dstFile 我们压缩后将压缩文件放到哪个目录
	 */
	public static void zipFile(String srcFile, String dstFile) {
		
		//创建输出流
		OutputStream os = null;
		ObjectOutputStream oos = null;
		//创建文件的输入流
		FileInputStream is = null;
		try {
			//创建文件的输入流
			is = new FileInputStream(srcFile);
			//创建一个和源文件大小一样的byte[]
			byte[] b = new byte[is.available()];
			//读取文件
			is.read(b);
			//直接对源文件压缩
			byte[] huffmanBytes = huffmanZip(b);
			//创建文件的输出流, 存放压缩文件
			os = new FileOutputStream(dstFile);
			//创建一个和文件输出流关联的ObjectOutputStream
			oos = new ObjectOutputStream(os);
			//把 赫夫曼编码后的字节数组写入压缩文件
			oos.writeObject(huffmanBytes); //我们是把
			//这里我们以对象流的方式写入 赫夫曼编码，是为了以后我们恢复源文件时使用
			//注意一定要把赫夫曼编码 写入压缩文件
			oos.writeObject(huffmanCodes);
			
			
		}catch (Exception e) {
			// TODO: handle exception
			System.out.println(e.getMessage());
		}finally {
			try {
				is.close();
				oos.close();
				os.close();
			}catch (Exception e) {
				// TODO: handle exception
				System.out.println(e.getMessage());
			}
		}
		
	}
	
	//完成数据的解压
	//思路
	//1. 将huffmanCodeBytes [-88, -65, -56, -65, -56, -65, -55, 77, -57, 6, -24, -14, -117, -4, -60, -90, 28]
	//   重写先转成 赫夫曼编码对应的二进制的字符串 "1010100010111..."
	//2.  赫夫曼编码对应的二进制的字符串 "1010100010111..." =》 对照 赫夫曼编码  =》 "i like like like java do you like a java"
	
	
	//编写一个方法，完成对压缩数据的解码
	/**
	 * 
	 * @param huffmanCodes 赫夫曼编码表 map
	 * @param huffmanBytes 赫夫曼编码得到的字节数组
	 * @return 就是原来的字符串对应的数组
	 */
	private static byte[] decode(Map<Byte,String> huffmanCodes, byte[] huffmanBytes) {
		
		//1. 先得到 huffmanBytes 对应的 二进制的字符串 ， 形式 1010100010111...
		StringBuilder stringBuilder = new StringBuilder();
		//将byte数组转成二进制的字符串
		for(int i = 0; i < huffmanBytes.length; i++) {
			byte b = huffmanBytes[i];
			//判断是不是最后一个字节
			boolean flag = (i == huffmanBytes.length - 1);
			stringBuilder.append(byteToBitString(!flag, b));
		}
		//把字符串安装指定的赫夫曼编码进行解码
		//把赫夫曼编码表进行调换，因为反向查询 a->100 100->a
		Map<String, Byte>  map = new HashMap<String,Byte>();
		for(Map.Entry<Byte, String> entry: huffmanCodes.entrySet()) {
			map.put(entry.getValue(), entry.getKey());
		}
		
		//创建要给集合，存放byte
		List<Byte> list = new ArrayList<>();
		//i 可以理解成就是索引,扫描 stringBuilder 
		for(int  i = 0; i < stringBuilder.length(); ) {
			int count = 1; // 小的计数器
			boolean flag = true;
			Byte b = null;
			
			while(flag) {
				//1010100010111...
				//递增的取出 key 1 
				String key = stringBuilder.substring(i, i+count);//i 不动，让count移动，指定匹配到一个字符
				b = map.get(key);
				if(b == null) {//说明没有匹配到
					count++;
				}else {
					//匹配到
					flag = false;
				}
			}
			list.add(b);
			i += count;//i 直接移动到 count	
		}
		//当for循环结束后，我们list中就存放了所有的字符  "i like like like java do you like a java"
		//把list 中的数据放入到byte[] 并返回
		byte b[] = new byte[list.size()];
		for(int i = 0;i < b.length; i++) {
			b[i] = list.get(i);
		}
		return b;
		
	}
 	
	/**
	 * 将一个byte 转成一个二进制的字符串, 如果看不懂，可以参考我讲的Java基础 二进制的原码，反码，补码
	 * @param b 传入的 byte
	 * @param flag 标志是否需要补高位如果是true ，表示需要补高位，如果是false表示不补, 如果是最后一个字节，无需补高位
	 * @return 是该b 对应的二进制的字符串，（注意是按补码返回）
	 */
	private static String byteToBitString(boolean flag, byte b) {
		//使用变量保存 b
		int temp = b; //将 b 转成 int
		//如果是正数我们还存在补高位
		if(flag) {
			temp |= 256; //按位与 256  1 0000 0000  | 0000 0001 => 1 0000 0001
		}
		String str = Integer.toBinaryString(temp); //返回的是temp对应的二进制的补码
		if(flag) {
			return str.substring(str.length() - 8);
		} else {
			return str;
		}
	}
	
	//使用一个方法，将前面的方法封装起来，便于我们的调用.
	/**
	 * 
	 * @param bytes 原始的字符串对应的字节数组
	 * @return 是经过 赫夫曼编码处理后的字节数组(压缩后的数组)
	 */
	private static byte[] huffmanZip(byte[] bytes) {
		List<Node> nodes = getNodes(bytes);
		//根据 nodes 创建的赫夫曼树
		Node huffmanTreeRoot = createHuffmanTree(nodes);
		//对应的赫夫曼编码(根据 赫夫曼树)
		Map<Byte, String> huffmanCodes = getCodes(huffmanTreeRoot);
		//根据生成的赫夫曼编码，压缩得到压缩后的赫夫曼编码字节数组
		byte[] huffmanCodeBytes = zip(bytes, huffmanCodes);
		return huffmanCodeBytes;
	}
	
	
	//编写一个方法，将字符串对应的byte[] 数组，通过生成的赫夫曼编码表，返回一个赫夫曼编码 压缩后的byte[]
	/**
	 * 
	 * @param bytes 这时原始的字符串对应的 byte[]
	 * @param huffmanCodes 生成的赫夫曼编码map
	 * @return 返回赫夫曼编码处理后的 byte[] 
	 * 举例： String content = "i like like like java do you like a java"; =》 byte[] contentBytes = content.getBytes();
	 * 返回的是 字符串 "1010100010111111110010001011111111001000101111111100100101001101110001110000011011101000111100101000101111111100110001001010011011100"
	 * => 对应的 byte[] huffmanCodeBytes  ，即 8位对应一个 byte,放入到 huffmanCodeBytes
	 * huffmanCodeBytes[0] =  10101000(补码) => byte  [推导  10101000=> 10101000 - 1 => 10100111(反码)=> 11011000= -88 ]
	 * huffmanCodeBytes[1] = -88
	 */
	private static byte[] zip(byte[] bytes, Map<Byte, String> huffmanCodes) {
		
		//1.利用 huffmanCodes 将  bytes 转成  赫夫曼编码对应的字符串
		StringBuilder stringBuilder = new StringBuilder();
		//遍历bytes 数组 
		for(byte b: bytes) {
			stringBuilder.append(huffmanCodes.get(b));
		}
		
		//System.out.println("测试 stringBuilder~~~=" + stringBuilder.toString());
		
		//将 "1010100010111111110..." 转成 byte[]
		
		//统计返回  byte[] huffmanCodeBytes 长度
		//一句话 int len = (stringBuilder.length() + 7) / 8;
		int len;
		if(stringBuilder.length() % 8 == 0) {
			len = stringBuilder.length() / 8;
		} else {
			len = stringBuilder.length() / 8 + 1;
		}
		//创建 存储压缩后的 byte数组
		byte[] huffmanCodeBytes = new byte[len];
		int index = 0;//记录是第几个byte
		for (int i = 0; i < stringBuilder.length(); i += 8) { //因为是每8位对应一个byte,所以步长 +8
				String strByte;
				if(i+8 > stringBuilder.length()) {//不够8位
					strByte = stringBuilder.substring(i);
				}else{
					strByte = stringBuilder.substring(i, i + 8);
				}	
				//将strByte 转成一个byte,放入到 huffmanCodeBytes
				huffmanCodeBytes[index] = (byte)Integer.parseInt(strByte, 2);
				index++;
		}
		return huffmanCodeBytes;
	}
	
	//生成赫夫曼树对应的赫夫曼编码
	//思路:
	//1. 将赫夫曼编码表存放在 Map<Byte,String> 形式
	//   生成的赫夫曼编码表{32=01, 97=100, 100=11000, 117=11001, 101=1110, 118=11011, 105=101, 121=11010, 106=0010, 107=1111, 108=000, 111=0011}
	static Map<Byte, String> huffmanCodes = new HashMap<Byte,String>();
	//2. 在生成赫夫曼编码表示，需要去拼接路径, 定义一个StringBuilder 存储某个叶子结点的路径
	static StringBuilder stringBuilder = new StringBuilder();
	
	
	//为了调用方便，我们重载 getCodes
	private static Map<Byte, String> getCodes(Node root) {
		if(root == null) {
			return null;
		}
		//处理root的左子树
		getCodes(root.left, "0", stringBuilder);
		//处理root的右子树
		getCodes(root.right, "1", stringBuilder);
		return huffmanCodes;
	}
	
	/**
	 * 功能：将传入的node结点的所有叶子结点的赫夫曼编码得到，并放入到huffmanCodes集合
	 * @param node  传入结点
	 * @param code  路径： 左子结点是 0, 右子结点 1
	 * @param stringBuilder 用于拼接路径
	 */
	private static void getCodes(Node node, String code, StringBuilder stringBuilder) {
		StringBuilder stringBuilder2 = new StringBuilder(stringBuilder);
		//将code 加入到 stringBuilder2
		stringBuilder2.append(code);
		if(node != null) { //如果node == null不处理
			//判断当前node 是叶子结点还是非叶子结点
			if(node.data == null) { //非叶子结点
				//递归处理
				//向左递归
				getCodes(node.left, "0", stringBuilder2);
				//向右递归
				getCodes(node.right, "1", stringBuilder2);
			} else { //说明是一个叶子结点
				//就表示找到某个叶子结点的最后
				huffmanCodes.put(node.data, stringBuilder2.toString());
			}
		}
	}
	
	//前序遍历的方法
	private static void preOrder(Node root) {
		if(root != null) {
			root.preOrder();
		}else {
			System.out.println("赫夫曼树为空");
		}
	}
	
	/**
	 * 
	 * @param bytes 接收字节数组
	 * @return 返回的就是 List 形式   [Node[date=97 ,weight = 5], Node[]date=32,weight = 9]......],
	 */
	private static List<Node> getNodes(byte[] bytes) {
		
		//1创建一个ArrayList
		ArrayList<Node> nodes = new ArrayList<Node>();
		
		//遍历 bytes , 统计 每一个byte出现的次数->map[key,value]
		Map<Byte, Integer> counts = new HashMap<>();
		for (byte b : bytes) {
			Integer count = counts.get(b);
			if (count == null) { // Map还没有这个字符数据,第一次
				counts.put(b, 1);
			} else {
				counts.put(b, count + 1);
			}
		}
		
		//把每一个键值对转成一个Node 对象，并加入到nodes集合
		//遍历map
		for(Map.Entry<Byte, Integer> entry: counts.entrySet()) {
			nodes.add(new Node(entry.getKey(), entry.getValue()));
		}
		return nodes;
		
	}
	
	//可以通过List 创建对应的赫夫曼树
	private static Node createHuffmanTree(List<Node> nodes) {
		
		while(nodes.size() > 1) {
			//排序, 从小到大
			Collections.sort(nodes);
			//取出第一颗最小的二叉树
			Node leftNode = nodes.get(0);
			//取出第二颗最小的二叉树
			Node rightNode = nodes.get(1);
			//创建一颗新的二叉树,它的根节点 没有data, 只有权值
			Node parent = new Node(null, leftNode.weight + rightNode.weight);
			parent.left = leftNode;
			parent.right = rightNode;
			
			//将已经处理的两颗二叉树从nodes删除
			nodes.remove(leftNode);
			nodes.remove(rightNode);
			//将新的二叉树，加入到nodes
			nodes.add(parent);
			
		}
		//nodes 最后的结点，就是赫夫曼树的根结点
		return nodes.get(0);
		
	}
	

}



//创建Node ,待数据和权值
class Node implements Comparable<Node>  {
	Byte data; // 存放数据(字符)本身，比如'a' => 97 ' ' => 32
	int weight; //权值, 表示字符出现的次数
	Node left;//
	Node right;
	public Node(Byte data, int weight) {
		
		this.data = data;
		this.weight = weight;
	}
	@Override
	public int compareTo(Node o) {
		// 从小到大排序
		return this.weight - o.weight;
	}
	
	public String toString() {
		return "Node [data = " + data + " weight=" + weight + "]";
	}
	
	//前序遍历
	public void preOrder() {
		System.out.println(this);
		if(this.left != null) {
			this.left.preOrder();
		}
		if(this.right != null) {
			this.right.preOrder();
		}
	}
}

哈夫曼编码压缩文件注意事项

六、二叉排序树

1.介绍

2.创建和遍历

3.删除

4.代码实现

public class BinarySortTreeDemo {
    public static void main(String[] args) {
        
    }
}

class BinarySortTree {
    private Node root;

    public Node getRoot() {
        return root;
    }

    //查找要删除的结点
    public Node search(int value) {
        if(root == null) {
            return null;
        } else {
            return root.search(value);
        }
    }

    //查找父结点
    public Node searchParent(int value) {
        if(root == null) {
            return null;
        } else {
            return root.searchParent(value);
        }
    }

    //编写方法:
    //1. 返回的 以node 为根结点的二叉排序树的最小结点的值
    //2. 删除node 为根结点的二叉排序树的最小结点
    /**
     *
     * @param node 传入的结点(当做二叉排序树的根结点)
     * @return 返回的 以node 为根结点的二叉排序树的最小结点的值
     */
    public int delRightTreeMin(Node node) {
        Node target = node;
        //循环的查找左子节点，就会找到最小值
        while(target.left != null) {
            target = target.left;
        }
        //这时 target就指向了最小结点
        //删除最小结点
        delNode(target.value);
        return target.value;
    }


    //删除结点
    public void delNode(int value) {
        if(root == null) {
            return;
        }else {
            //1.需求先去找到要删除的结点  targetNode
            Node targetNode = search(value);
            //如果没有找到要删除的结点
            if(targetNode == null) {
                return;
            }
            //如果我们发现当前这颗二叉排序树只有一个结点
            if(root.left == null && root.right == null) {
                root = null;
                return;
            }

            //去找到targetNode的父结点
            Node parent = searchParent(value);
            //如果要删除的结点是叶子结点
            if(targetNode.left == null && targetNode.right == null) {
                //判断targetNode 是父结点的左子结点，还是右子结点
                if(parent.left != null && parent.left.value == value) { //是左子结点
                    parent.left = null;
                } else if (parent.right != null && parent.right.value == value) {//是由子结点
                    parent.right = null;
                }
            } else if (targetNode.left != null && targetNode.right != null) { //删除有两颗子树的节点
                int minVal = delRightTreeMin(targetNode.right);
                targetNode.value = minVal;


            } else { // 删除只有一颗子树的结点
                //如果要删除的结点有左子结点
                if(targetNode.left != null) {
                    if(parent != null) {
                        //如果 targetNode 是 parent 的左子结点
                        if(parent.left.value == value) {
                            parent.left = targetNode.left;
                        } else { //  targetNode 是 parent 的右子结点
                            parent.right = targetNode.left;
                        }
                    } else {
                        root = targetNode.left;
                    }
                } else { //如果要删除的结点有右子结点
                    if(parent != null) {
                        //如果 targetNode 是 parent 的左子结点
                        if(parent.left.value == value) {
                            parent.left = targetNode.right;
                        } else { //如果 targetNode 是 parent 的右子结点
                            parent.right = targetNode.right;
                        }
                    } else {
                        root = targetNode.right;
                    }
                }

            }

        }
    }

    //添加结点的方法
    public void add(Node node) {
        if(root == null) {
            root = node;//如果root为空则直接让root指向node
        } else {
            root.add(node);
        }
    }
    //中序遍历
    public void infixOrder() {
        if(root != null) {
            root.infixOrder();
        } else {
            System.out.println("二叉排序树为空，不能遍历");
        }
    }
}

class Node {
    int value;
    Node left;
    Node right;
    public Node(int value) {
        this.value = value;
    }

    //查找要删除的结点
    /**
     *
     * @param value 希望删除的结点的值
     * @return 如果找到返回该结点，否则返回null
     */
    public Node search(int value) {
        if(value == this.value) { //找到就是该结点
            return this;
        } else if(value < this.value) {//如果查找的值小于当前结点，向左子树递归查找
            //如果左子结点为空
            if(this.left  == null) {
                return null;
            }
            return this.left.search(value);
        } else { //如果查找的值不小于当前结点，向右子树递归查找
            if(this.right == null) {
                return null;
            }
            return this.right.search(value);
        }

    }
    //查找要删除结点的父结点
    /**
     *
     * @param value 要找到的结点的值
     * @return 返回的是要删除的结点的父结点，如果没有就返回null
     */
    public Node searchParent(int value) {
        //如果当前结点就是要删除的结点的父结点，就返回
        if((this.left != null && this.left.value == value) ||
                (this.right != null && this.right.value == value)) {
            return this;
        } else {
            //如果查找的值小于当前结点的值, 并且当前结点的左子结点不为空
            if(value < this.value && this.left != null) {
                return this.left.searchParent(value); //向左子树递归查找
            } else if (value >= this.value && this.right != null) {
                return this.right.searchParent(value); //向右子树递归查找
            } else {
                return null; // 没有找到父结点
            }
        }

    }

    @Override
    public String toString() {
        return "Node [value=" + value + "]";
    }

    public void add(Node node) {
        if(node == null) {
            return;
        }

        //判断传入的结点的值，和当前子树的根结点的值关系
        if(node.value < this.value) {
            //如果当前结点左子结点为null
            if(this.left == null) {
                this.left = node;
            } else {
                //递归的向左子树添加
                this.left.add(node);
            }
        } else { //添加的结点的值大于 当前结点的值
            if(this.right == null) {
                this.right = node;
            } else {
                //递归的向右子树添加
                this.right.add(node);
            }

        }
    }

    //中序遍历
    public void infixOrder() {
        if(this.left != null) {
            this.left.infixOrder();
        }
        System.out.println(this);
        if(this.right != null) {
            this.right.infixOrder();
        }
    }

}

七、平衡二叉树（AVL树）

1.介绍

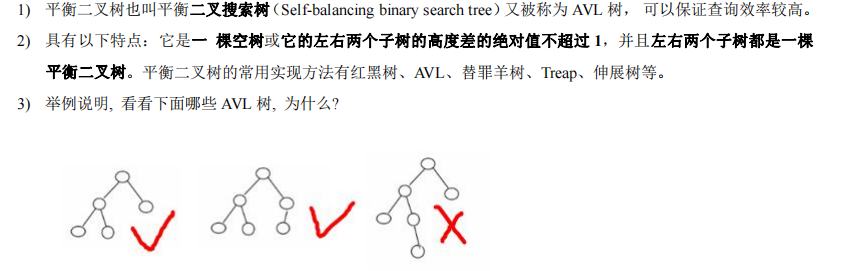
2.思路分析

3.代码实现

public class AVLTreeDemo {

	public static void main(String[] args) {
		//int[] arr = {4,3,6,5,7,8};
		//int[] arr = { 10, 12, 8, 9, 7, 6 };
		int[] arr = { 10, 11, 7, 6, 8, 9 };  
		//创建一个 AVLTree对象
		AVLTree avlTree = new AVLTree();
		//添加结点
		for(int i=0; i < arr.length; i++) {
			avlTree.add(new Node(arr[i]));
		}
		
		//遍历
		System.out.println("中序遍历");
		avlTree.infixOrder();
		
		System.out.println("在平衡处理~~");
		System.out.println("树的高度=" + avlTree.getRoot().height()); //3
		System.out.println("树的左子树高度=" + avlTree.getRoot().leftHeight()); // 2
		System.out.println("树的右子树高度=" + avlTree.getRoot().rightHeight()); // 2
		System.out.println("当前的根结点=" + avlTree.getRoot());//8
		
		
	}

}

// 创建AVLTree
class AVLTree {
	private Node root;

	public Node getRoot() {
		return root;
	}

	// 查找要删除的结点
	public Node search(int value) {
		if (root == null) {
			return null;
		} else {
			return root.search(value);
		}
	}

	// 查找父结点
	public Node searchParent(int value) {
		if (root == null) {
			return null;
		} else {
			return root.searchParent(value);
		}
	}

	// 编写方法:
	// 1. 返回的 以node 为根结点的二叉排序树的最小结点的值
	// 2. 删除node 为根结点的二叉排序树的最小结点
	/**
	 * 
	 * @param node
	 *            传入的结点(当做二叉排序树的根结点)
	 * @return 返回的 以node 为根结点的二叉排序树的最小结点的值
	 */
	public int delRightTreeMin(Node node) {
		Node target = node;
		// 循环的查找左子节点，就会找到最小值
		while (target.left != null) {
			target = target.left;
		}
		// 这时 target就指向了最小结点
		// 删除最小结点
		delNode(target.value);
		return target.value;
	}

	// 删除结点
	public void delNode(int value) {
		if (root == null) {
			return;
		} else {
			// 1.需求先去找到要删除的结点 targetNode
			Node targetNode = search(value);
			// 如果没有找到要删除的结点
			if (targetNode == null) {
				return;
			}
			// 如果我们发现当前这颗二叉排序树只有一个结点
			if (root.left == null && root.right == null) {
				root = null;
				return;
			}

			// 去找到targetNode的父结点
			Node parent = searchParent(value);
			// 如果要删除的结点是叶子结点
			if (targetNode.left == null && targetNode.right == null) {
				// 判断targetNode 是父结点的左子结点，还是右子结点
				if (parent.left != null && parent.left.value == value) { // 是左子结点
					parent.left = null;
				} else if (parent.right != null && parent.right.value == value) {// 是由子结点
					parent.right = null;
				}
			} else if (targetNode.left != null && targetNode.right != null) { // 删除有两颗子树的节点
				int minVal = delRightTreeMin(targetNode.right);
				targetNode.value = minVal;

			} else { // 删除只有一颗子树的结点
				// 如果要删除的结点有左子结点
				if (targetNode.left != null) {
					if (parent != null) {
						// 如果 targetNode 是 parent 的左子结点
						if (parent.left.value == value) {
							parent.left = targetNode.left;
						} else { // targetNode 是 parent 的右子结点
							parent.right = targetNode.left;
						}
					} else {
						root = targetNode.left;
					}
				} else { // 如果要删除的结点有右子结点
					if (parent != null) {
						// 如果 targetNode 是 parent 的左子结点
						if (parent.left.value == value) {
							parent.left = targetNode.right;
						} else { // 如果 targetNode 是 parent 的右子结点
							parent.right = targetNode.right;
						}
					} else {
						root = targetNode.right;
					}
				}

			}

		}
	}

	// 添加结点的方法
	public void add(Node node) {
		if (root == null) {
			root = node;// 如果root为空则直接让root指向node
		} else {
			root.add(node);
		}
	}

	// 中序遍历
	public void infixOrder() {
		if (root != null) {
			root.infixOrder();
		} else {
			System.out.println("二叉排序树为空，不能遍历");
		}
	}
}

// 创建Node结点
class Node {
	int value;
	Node left;
	Node right;

	public Node(int value) {

		this.value = value;
	}

	// 返回左子树的高度
	public int leftHeight() {
		if (left == null) {
			return 0;
		}
		return left.height();
	}

	// 返回右子树的高度
	public int rightHeight() {
		if (right == null) {
			return 0;
		}
		return right.height();
	}

	// 返回 以该结点为根结点的树的高度
	public int height() {
		return Math.max(left == null ? 0 : left.height(), right == null ? 0 : right.height()) + 1;
	}
	
	//左旋转方法
	private void leftRotate() {
		
		//创建新的结点，以当前根结点的值
		Node newNode = new Node(value);
		//把新的结点的左子树设置成当前结点的左子树
		newNode.left = left;
		//把新的结点的右子树设置成带你过去结点的右子树的左子树
		newNode.right = right.left;
		//把当前结点的值替换成右子结点的值
		value = right.value;
		//把当前结点的右子树设置成当前结点右子树的右子树
		right = right.right;
		//把当前结点的左子树(左子结点)设置成新的结点
		left = newNode;
		
		
	}
	
	//右旋转
	private void rightRotate() {
		Node newNode = new Node(value);
		newNode.right = right;
		newNode.left = left.right;
		value = left.value;
		left = left.left;
		right = newNode;
	}

	// 查找要删除的结点
	/**
	 * 
	 * @param value
	 *            希望删除的结点的值
	 * @return 如果找到返回该结点，否则返回null
	 */
	public Node search(int value) {
		if (value == this.value) { // 找到就是该结点
			return this;
		} else if (value < this.value) {// 如果查找的值小于当前结点，向左子树递归查找
			// 如果左子结点为空
			if (this.left == null) {
				return null;
			}
			return this.left.search(value);
		} else { // 如果查找的值不小于当前结点，向右子树递归查找
			if (this.right == null) {
				return null;
			}
			return this.right.search(value);
		}

	}

	// 查找要删除结点的父结点
	/**
	 * 
	 * @param value
	 *            要找到的结点的值
	 * @return 返回的是要删除的结点的父结点，如果没有就返回null
	 */
	public Node searchParent(int value) {
		// 如果当前结点就是要删除的结点的父结点，就返回
		if ((this.left != null && this.left.value == value) || (this.right != null && this.right.value == value)) {
			return this;
		} else {
			// 如果查找的值小于当前结点的值, 并且当前结点的左子结点不为空
			if (value < this.value && this.left != null) {
				return this.left.searchParent(value); // 向左子树递归查找
			} else if (value >= this.value && this.right != null) {
				return this.right.searchParent(value); // 向右子树递归查找
			} else {
				return null; // 没有找到父结点
			}
		}

	}

	@Override
	public String toString() {
		return "Node [value=" + value + "]";
	}

	// 添加结点的方法
	// 递归的形式添加结点，注意需要满足二叉排序树的要求
	public void add(Node node) {
		if (node == null) {
			return;
		}

		// 判断传入的结点的值，和当前子树的根结点的值关系
		if (node.value < this.value) {
			// 如果当前结点左子结点为null
			if (this.left == null) {
				this.left = node;
			} else {
				// 递归的向左子树添加
				this.left.add(node);
			}
		} else { // 添加的结点的值大于 当前结点的值
			if (this.right == null) {
				this.right = node;
			} else {
				// 递归的向右子树添加
				this.right.add(node);
			}

		}
		
		//当添加完一个结点后，如果: (右子树的高度-左子树的高度) > 1 , 左旋转
		if(rightHeight() - leftHeight() > 1) {
			//如果它的右子树的左子树的高度大于它的右子树的右子树的高度
			if(right != null && right.leftHeight() > right.rightHeight()) {
				//先对右子结点进行右旋转
				right.rightRotate();
				//然后在对当前结点进行左旋转
				leftRotate(); //左旋转..
			} else {
				//直接进行左旋转即可
				leftRotate();
			}
			return ; //必须要!!!
		}
		
		//当添加完一个结点后，如果 (左子树的高度 - 右子树的高度) > 1, 右旋转
		if(leftHeight() - rightHeight() > 1) {
			//如果它的左子树的右子树高度大于它的左子树的高度
			if(left != null && left.rightHeight() > left.leftHeight()) {
				//先对当前结点的左结点(左子树)->左旋转
				left.leftRotate();
				//再对当前结点进行右旋转
				rightRotate();
			} else {
				//直接进行右旋转即可
				rightRotate();
			}
		}
	}

	// 中序遍历
	public void infixOrder() {
		if (this.left != null) {
			this.left.infixOrder();
		}
		System.out.println(this);
		if (this.right != null) {
			this.right.infixOrder();
		}
	}

}

八、多路查找树

1.二叉树与B树

（1）问题分析

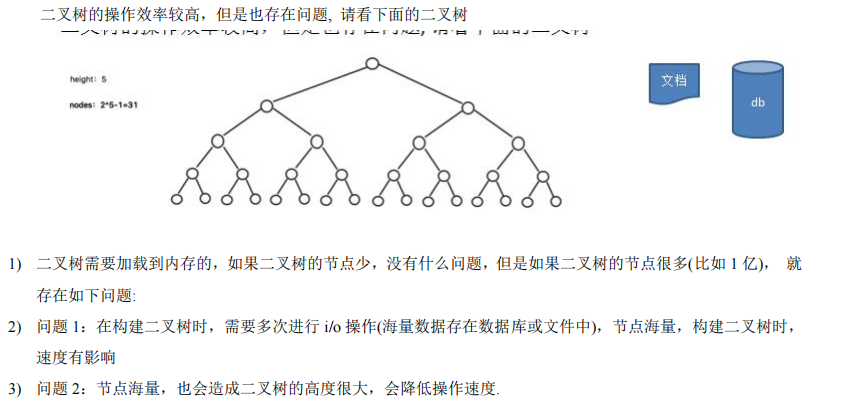
（2）多叉树

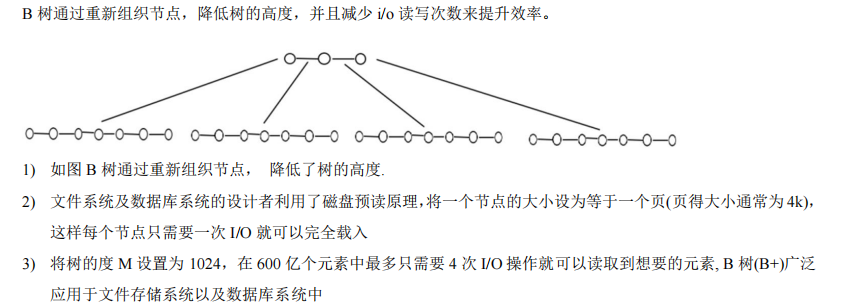
（3）B树基本介绍

2.2-3树

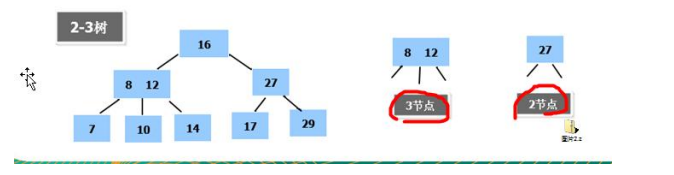
（1）特点

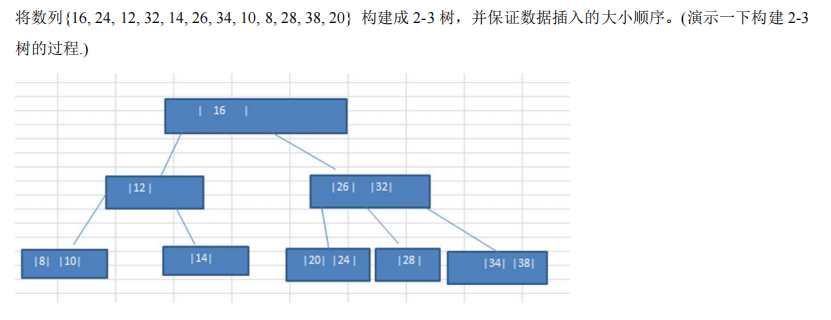
（2）应用案例

（3）其他说明

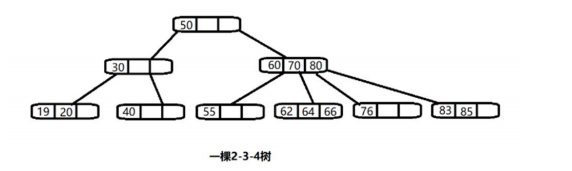
3.B树、B+树和B*树

（1）B树介绍

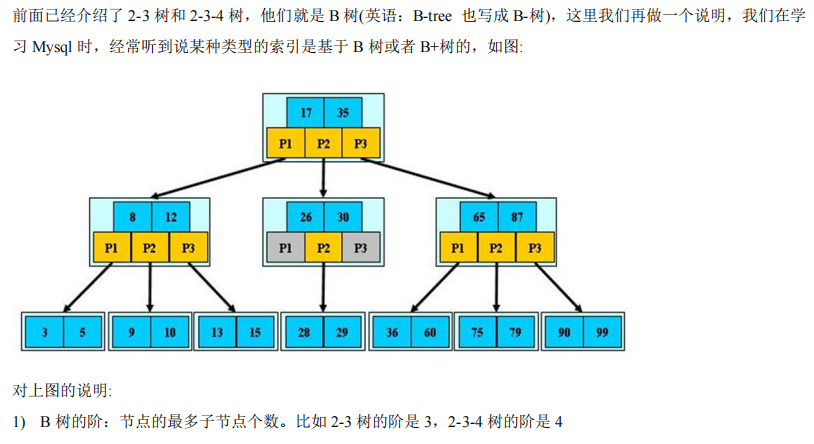
（2）B+树的介绍

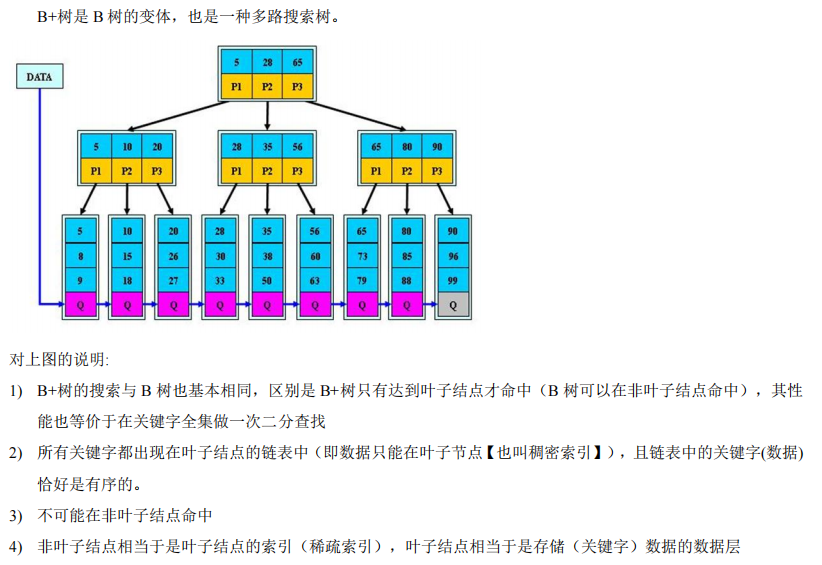
（3）B*树的介绍

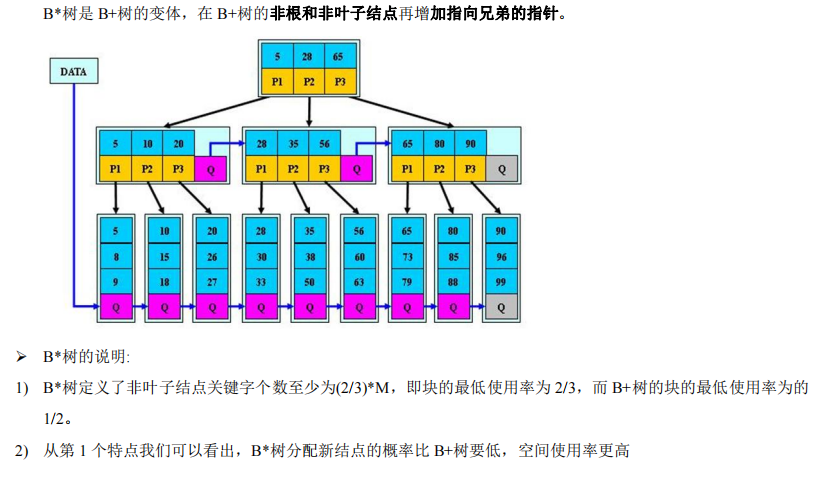
e);
}

	}
	
	//当添加完一个结点后，如果: (右子树的高度-左子树的高度) > 1 , 左旋转
	if(rightHeight() - leftHeight() > 1) {
		//如果它的右子树的左子树的高度大于它的右子树的右子树的高度
		if(right != null && right.leftHeight() > right.rightHeight()) {
			//先对右子结点进行右旋转
			right.rightRotate();
			//然后在对当前结点进行左旋转
			leftRotate(); //左旋转..
		} else {
			//直接进行左旋转即可
			leftRotate();
		}
		return ; //必须要!!!
	}
	
	//当添加完一个结点后，如果 (左子树的高度 - 右子树的高度) > 1, 右旋转
	if(leftHeight() - rightHeight() > 1) {
		//如果它的左子树的右子树高度大于它的左子树的高度
		if(left != null && left.rightHeight() > left.leftHeight()) {
			//先对当前结点的左结点(左子树)->左旋转
			left.leftRotate();
			//再对当前结点进行右旋转
			rightRotate();
		} else {
			//直接进行右旋转即可
			rightRotate();
		}
	}
}

// 中序遍历
public void infixOrder() {
	if (this.left != null) {
		this.left.infixOrder();
	}
	System.out.println(this);
	if (this.right != null) {
		this.right.infixOrder();
	}
}

}

### 八、多路查找树

#### 1.二叉树与B树

##### （1）问题分析

[外链图片转存中...(img-5Cz20Sj3-1648727567011)]

##### （2）多叉树

[外链图片转存中...(img-MLfgGaeG-1648727567011)]

[外链图片转存中...(img-3VoCCeVv-1648727567012)]

##### （3）B树基本介绍

[外链图片转存中...(img-8f1ZSSjn-1648727567012)]

#### 2.2-3树

##### （1）特点

[外链图片转存中...(img-SEvFyLC4-1648727567012)]

[外链图片转存中...(img-zlzgeHmQ-1648727567012)]

##### （2）应用案例

[外链图片转存中...(img-CPxxIqXk-1648727567013)]

[外链图片转存中...(img-sobeZVc9-1648727567013)]

##### （3）其他说明

[外链图片转存中...(img-Zx8iZE1f-1648727567013)]

[外链图片转存中...(img-INWYLmo0-1648727567013)]

#### 3.B树、B+树和B*树

##### （1）B树介绍

[外链图片转存中...(img-4zSaqsx1-1648727567014)]

[外链图片转存中...(img-CqzhWPEg-1648727567014)]

[外链图片转存中...(img-Z1viKh3A-1648727567014)]

##### （2）B+树的介绍

[外链图片转存中...(img-L3kx5dRe-1648727567014)]

[外链图片转存中...(img-DAzBRjE7-1648727567015)]

##### （3）B*树的介绍

[外链图片转存中...(img-drzb0RB4-1648727567015)]