从 P≠NP 的验证不对称到 Meta ⼤挖 AI 天才：AI 突破的下一个拐点？

引子

Meta又宣布已从OpenAI挖来了顶尖研究员，其中就包括Jason Wei，他主攻强化学习和深度研究的核心成员。这一跳槽震动了业界，并引发了大量媒体和关键人物的关注。Jason Wei 将加入 Meta 全新 Superintelligence Lab，前 Slack 账号已被停用，这与 Wei 专注 o1/o3 模型、强化学习背景密切相关 (WIRED)。而此次是 Meta AI 挖才大战中的一环，据称总预算高达 3 亿美元，Dell CEO 更对 Zuckerberg 此举发出“警告”。 媒体报导确认 Wei 与同伴 Hyung Won Chung 一同加盟 Meta，称这是 Zuckerberg 针对 AGI 战略的重要布局 (TC)。 Wei 此前在 Google 和 OpenAI 均有深厚研究背景，并在社媒重申对增强学习哲学的热情 (Tech Times)。

Jason Wei

 

👥 关键人物反应

• LinkedIn News 编辑 Emma Thorne 指出，Meta 瞄准的正是曾共事于 Google/OpenAI 的研究团队，以“协同效应”为核心招聘策略 。

• 技术工程师 Tony Ndezwa Omula 在 LinkedIn 评论中称：“Meta 明显在组装合作已久的研究组合，借此加速 AGI 实现”，凸显此举战略深度 (LinkedIn)。

• Pablo Carmona 表示两人在跳槽前就关闭 OpenAI Slack，表明高层级离职紧迫感和团队流动趋势 (LinkedIn)。

• Harnoor Singh 在 GenAI Week SF 指出，Wei 在会上分享的“jagged edge of intelligence”观点引发热议，他的观点将有机会在 Meta Superintelligence Labs 中继续发光 (LinkedIn)。

总体来看，这次跳槽不仅是一次人才流动，也是围绕“AGI 实现路径”的战略比拼。Meta通过重金招揽深研强化学习与推理模型的团队，展现其野心与野性，也迫使 OpenAI、Anthropic 等迅速反应。

JASON WEI 介绍

Jason Wei 曾任职于 Google Brain（2020–2023），其间主导或参与了多项影响深远的研究工作，包括：

• Chain‑of‑Thought（思维链）Prompting：提出通过在提示中加入“chain-of-thought”示例，使大模型展现分步推理能力，从而在算术、常识推理和符号操作等任务上达到更高表现 (arXiv)；同时，Jason Wei 对 self-consistency 系统化探索，也为模型推理能力的发展奠定了基础 (arXiv)；

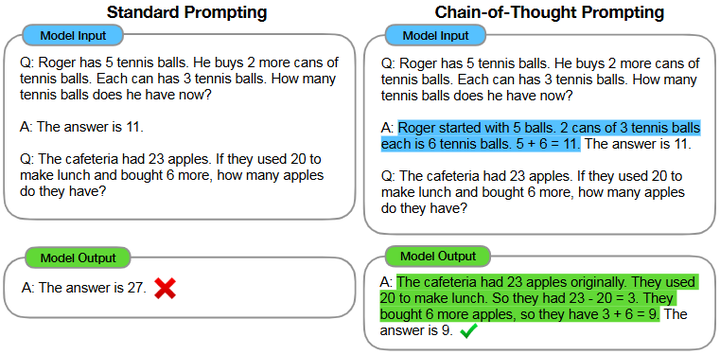
Chain-of-thought prompting

• Instruction Tuning（指令微调）：为模型提供更广泛、复杂的指令样本，显著提升其zero-shot 推理泛化能力 ；

• Emergent Phenomena（涌现能力）：与团队合作系统性研究了当模型规模增加时涌现出的新能力 (arXiv)。

在 OpenAI（2023–2025）期间，他继续深耕模型推理与强化学习技术，负责的是 o1 和 deep research 项目：

• o1 模型：OpenAI 首个能够“先思考、再输出”的推理型大模型，实现了在复杂科学、数学、编程任务上的大幅进步 ；

• 深度研究 (deep research)：推动强化学习、人类反馈（RLHF）、推理机制的结合与优化。

Jason Wei 的研究之旅是一条 从理论到落地、从 Google 到 OpenAI，再至 Meta 的脉络清晰、飞跃不断的路径。他不仅推动了链式推理、指令微调与涌现能力的理论突破，也将强化学习和验证机制引入模型训练流程。此次加入 Meta，或许预示着其验证者思想将在超级智能构建中发挥更大作用，也为 AI 科普和产业写下新的篇章。

🚀 与Meta 的技术路径规划完全契合

有业内人士分析，Wei 的强化学习理念与验证机制主张，正好契合 Meta 对“on-policy 结构、自我验证闭环”的技术野心 (WIRED)。

Superintelligence Lab 的设立与野心

Meta 在 2025 年底设立了 Superintelligence Lab（MSL），由 Alexandr Wang（前 Scale AI CEO）和 Nat Friedman（前 GitHub CEO）联合领导，旨在整合其基础模型、AI 产品及研究团队，全面部署 AGI 级技术研发战略 。这一实验室标志着 Meta 不只是追赶，而是要构建“超越人类”的智能体系，并将研究方向从“生成”升级到“推理＋验证” 。

强化学习与 on-policy 结构的重视

Meta 广泛挖掘强化学习与推理模型人才，比如招募 Jason Wei（一贯强调 on-policy RL 和 chain‑of‑thought 结构）、Chung 等专家；同时从 DeepMind、OpenAI、Anthropic 挖角编织 RL 团队 (WIRED)。强化学习尤其 on-policy 结构，将是他们从“思考”转向“自主验证”路径的核心支撑。

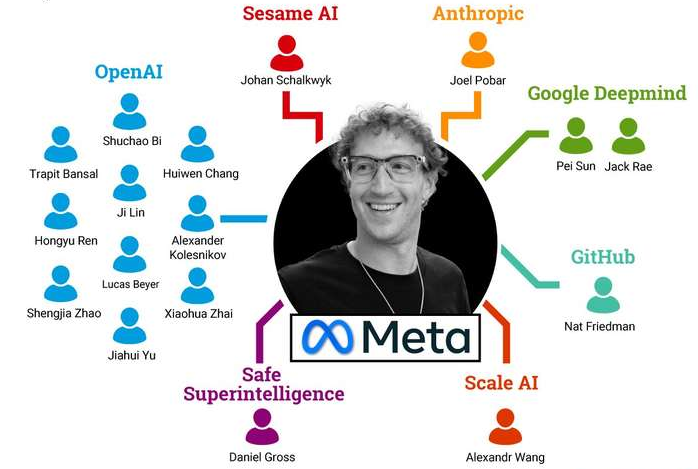
Superintelligence Lab group members

自我验证闭环：推理＋验证结合

Meta 特别关注开发出能持续验证、评估自身推理的闭环系统：

• TechCrunch 指出，Meta 将建立“推理模型”，让代理智能先思考、再输出答案，并依靠自动验证模块进行自我反馈 (TC)。

• Superintelligence Lab 的愿景在于将推理、验证与强化学习融为一体，迈向自主优化、自我迭代的 AGI 能力 (Enterprise Technology Association)。

资源+结构齐备，目标可验证性突破

• 财力支持：Meta 针对 AGI 实验大手笔投入——包括 $14.3B 投资给 Scale AI、数百亿美元基础设施开支及上亿美元薪资待遇 。扎克伯格指出，顶尖 AI 研究员在考虑加入一家公司时，除了薪资之外，最关心的是“管理下属越少越好，以及能拿到最多的 GPU 资源”（LinkedIn）。扎克伯格补充，研究员还渴望“从零开始创建实验室环境”，以避免受限于遗留系统的束缚 。 据他所言，这种“硬件主权”使 Meta 在人才争夺中脱颖而出，因为研究者可以“按需大规模试验”。他提到，不少候选人会在面试早期就询问“能支配多少算力”，将 GPU 数量视为首要考量 （WinBuzzer）。 这一观点也获得行业同行印证，Perplexity 创始人 Aravind Srinivas 曾提到有人要求“先备齐一万块 H100 再谈”（Business Insider）。

• 开放策略：通过开源 Llama 模型、搭配自研的 MTIA 芯片、Scale 的数据生态支持，Meta 可以快速进行“验证-生成-迭代”机制测试 (AInvest)。

MTIA

在这种背景下，Jason Wei 所提出的“验证者法则”、chain‑of‑thought、on-policy 强化学习等理念，与 Meta 实现“超智能”路径的需求不谋而合。Meta 新实验室恐将成为这些理念首次大规模落地的试验平台，这是Meta的大招吗 ？

Jason Wei唱的是什么戏？

Jason Wei's Blog

🎭 第一幕：隐秘的觉醒 —— “验证者法则”问世

就在跳槽前后的7 月15日，Jason Wei 在自己博客上提出“验证不对称性”与“验证者法则”——这是一个深刻洞见：所有易于验证的任务，AI 终将攻克 ——他笔锋犀利，点明验证能力是 AI 应用的天花板，他用数独、LeetCode、Alpha Evolve（Deepmind） 等丰富案例铺垫其论，瞬间点燃了社区 。这一理论不仅是对 AI 基础训练机制的深入剖析，也道出了他对 AI 未来路径的预判：验证能力将决定 AI 的突破方向。

Jason Wei

🎭 第二幕：意志的宣言 —— “走自己的 RL 路”

紧接着，他在 X 上发声：

“模仿是好的，必须去做。但要想超越老师，就要走自己的路，冒险，并从环境中获取回报。”

这句既是生活哲学，也是他在强化学习中的信条 —— on-policy 即力量。这番话意在提醒，真正的进步需自主探索，而不是依赖他人成果 。

🎭 第三幕：理念与环境的共鸣

在 Meta，他将获得更大平台验证“验证者法则”：

• 资源狂热：Meta 套现 3 亿美元挖才，极大增强实验回路的可验证性；

• 团队协同：与 Chung 的长期合作将强化 on-policy 探索机制；

• 实验自由：Meta 超智能实验室为 RLHF、验证机制提供了前所未有的试验平台。

🎭 第四幕：未来的张力 —— 验证 VS 推理的殊途同归

这次跳槽，在剧场式叙述里呈现为：

1. 理论先行：Wei 以“验证者法则”揭示 AI 训练根本。

2. 探索宣言：他的 on-policy 戒启示录，预示更深层的实践之道。

3. 时代召唤：Meta 相中他理念，豪掷重金邀其加入超级智能研究阵营。

4. 化为行动：Wei 离开 OpenAI，正是他理念落地的壮丽旅程。

5. 未来悬念：将他的验证洞察融入 Meta，AI 能否突破“验证瓶颈”？ 或将决定下一个智能浪潮。

什么是验证不对称及验证法则？

Jason Wei 在《Asymmetry of verification and verifier’s law》阐释了“验证不对称性”（Asymmetry of Verification）与相应的“验证者法则”（Verifier’s Law）,这些思考和洞察深入借鉴了Alperen Keles 博客文章《Verifiability is the Limit》的论述。同时，Jason Wei在《life lessons from reinforcement learning》 将在策略（on‑policy）强化学习与我们应对人生挑战的方式进行了类比，强调要“超越老师”，必须走自己的道路，而不仅仅是模仿。

验证不对称性

定义与示例

• 验证不对称：有些任务验证起来非常简单，却极其难以解决，例如检验数独解是否正确远比构造解容易。

• 典型例子: 数独与填字游戏：解题需要穷举候选项并检查各种约束，而验证解答正确性仅需几秒钟。网站开发：完整开发如 Instagram 的前后端需耗费工程团队多年，但任何人都可迅速判断网站是否可用。编程竞赛题：Solving BrowseComp 问题需浏览数百站点，但验证一个给定答案通常只需直接搜索即可。

此外，Jason还指出有些任务验证与求解耗时相近（如对 900 位数求和），甚至存在难于验证的情形（如论述性文章的事实核查）。同样地，Alperen Keles 在其Blog中《verifiability is the-limit》指出，当下无论是“vibe coding”式的无人值守代理，还是带有自动补全功能的编程助手，都能将代码撰写环节大量交由 LLM，但验证（verification）环节依然离不开人类：验证不对称性——即验证一段代码是否符合预期，比真正编写这段代码要容易得多——形成了 LLM 在软件工程中应用的根本瓶颈。文章通过前端（UI）与后端（服务器）编程的对比，揭示了 UI 之所以在实践中更受欢迎，正是因为可通过“肉眼一瞥”快速验证；而后台服务需依赖复杂的测试输入与状态管理，验证成本高昂。

提升验证效率

• 前置研究：通过前置研究（front‑loading research），可以部分改善验证不对称性。例如，在数学竞赛中若已拿到答案密钥，检验答案几乎毫无难度。

• 测试用例与自动化验证：在编程题场景中，充分覆盖的测试用例能将人工读码和检查的繁琐工作转化为自动化流程，这正是 LeetCode 等平台所采用的方法 。

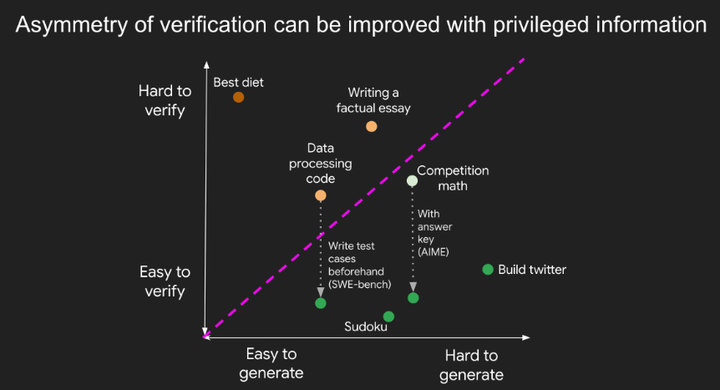
Improving asymmetry of verification

同时，Alperen Keles在《verifiability is the-limit》也强调，要突破这一瓶颈，单靠多代理系统（agentic approaches）不可行，必须发展面向验证的开发工具：如将测试自动摘要成可读断言、广泛采用属性测试（property-based testing），并扩充“正确性”（correctness）语汇以覆盖性能、安全性、可访问性等多维度度量。例如，将 LLM 生成的测试用例自动浓缩为可读断言，帮助开发者快速把握测试意图，但需防范信息丢失风险；鼓励使用声明式测试方法，由开发者定义输入‑输出谓词，自动生成大量随机样本，既易读又增强测试强度；通过契约（contracts）、不变量（invariants）等形式化约定，将更多非功能需求纳入自动验证流程。

验证者法则

法则陈述

验证者法则： “AI 训练某项任务的难易程度，与该任务的可验证性成正比。”只要任务易于验证，AI 终将掌握。

同样地，Alperen Keles指出任何软件系统在可执行阶段的最终瓶颈都来源于验证环节的成本与复杂度。其中，最为理想地完美验收器（Perfect Oracles）是游戏胜负或编程竞赛评测即为每次都能明确给出“对/错”的完美反馈，LLM 在此类场景已展现优异表现。

核心标准

要符合验证者法则，任务需满足： 客观真实性：对解的质量有明确共识。 快速可验证：几秒内即可检查解。 可扩展验收：可并行评估大量解。 低噪声：验证结果与实际质量高度相关。 连续奖励（可选）：能够对部分成功进行排序评分。 在Jason看来，当上述可验证性标准被满足时，神经网络可在每次梯度更新中获得丰富信号，加速迭代显著提升学习效率。那些易于验证的基准测试往往推动了快速的技术突破。

对实践者的建议：践行在策略实验——构建自己的反馈回路，而非过度依赖现有示例。 对基准设计者的建议：优先选择那些具备清晰、快速、可扩展验证机制的任务，以加速 AI 突破（参考下图）。 对研究者的建议：探索降低验证不对称性的方法，例如更丰富的奖励设计或自动化测试生成。 Jason Wei 强调，通过识别并优化任务的可验证性，我们不仅能理解过去 AI 突破的原因，也能指导未来基准与系统的设计，从而在更广泛的领域实现“凡可测，必可解”。而Alperen Keles期待 LLM 能在“玩转”完美验收器后，开发者可转向提出新定理、让 LLM 生成并验证代码及证明，并最终将系统部署到生产环境。

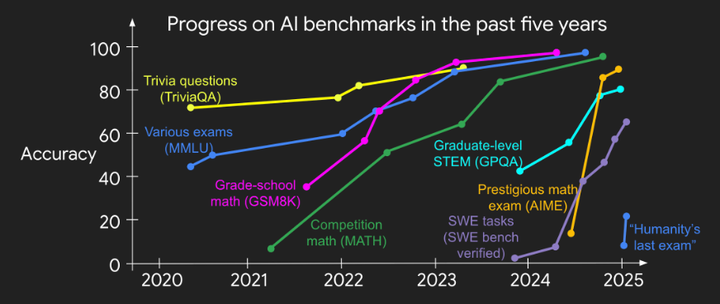
AI Benchmark Progress Over the Last Five Years

Jason Wei这是经验之谈，还是理论探讨呢？

验证的不对称性问题属于什么范畴的观点？

核心问题：衡量“找解”（solution-finding）与“验证解是否正确”（verification）的计算成本差异。这恰恰对应计算复杂性理论中的 P vs NP 问题：是否所有能被快速验证的问题（NP），都能被快速解决（P）？这是理论计算机科学中的中心未解问题之一 (Quanta Magazine)。更具体地，复杂性理论中的 决策复杂度（decidability）和验证复杂度（verifiability） 分支探讨这类问题的结构与边界 (Computer Science Stack Exchange)。

什么是 P 与 NP ？

• P（Polynomial time）：所有能被确定性图灵机在输入规模 n 的时间多项式内解决（判定）的决策问题组成的集合。

• NP（Nondeterministic Polynomial time）：所有能被非确定性图灵机在多项式时间内解决，或等价地，所有给定“证书”（certificate）后，确定性图灵机能在多项式时间内验证该证书正确性的决策问题集合。

Cook在1971年首次形式化地提出了这一问题：是否“每一个由非确定性机器在多项式时间内接受的语言，也能被某个确定性机器在多项式时间内接受”(Clay Mathematics Institute)。Clay数学研究所将其列为千禧年七大难题之一，悬赏一百万美元(Clay Mathematics Institute)。P vs NP 问题是理论计算机科学中最著名的未解难题之一，其核心在于询问“所有能在多项式时间内验证的问题，是否也能在多项式时间内求解”（即P =? NP）。尽管数十年来未能给出证明，但绝大多数专家（2019年调查中99%的专家）倾向于相信 P≠NP(维基百科)。研究者在受限计算模型（如电路、代数决策树）、非经典证明系统（如交互式证明、PCP 定理）等方向取得了部分下界或结构性结果，但总体难以突破“天然难题”的本质(CMU)。在 LLM 领域，虽然可以利用链式思考和自我批改（self‑verification）机制，赋予模型对候选答案的“快速检查”能力，但它们并不具备经典意义上多项式时间上的正确性保证，更多是经验性和启发式的验证手段(OpenReview)。

P 与 NP问题与 LLM 验证机制和强化学习（Reinforcement Learning,RL）的关联

从 NP 验证到 RL 环境构造

• 在复杂性理论中，NP 类问题是指可以在多项式时间内，令一个确定性机器（verifier）验证给定证书（certificate）是否正确的问题。P vs NP 核心就在于：是否每个 NP 问题也能在多项式时间内由确定性机器（即算法）直接求解维基百科。

• 在 RL 中，要训练智能体解决某个任务，首先需要构建一个环境，定义状态、动作及奖励函数；也即只有当我们能“验证”一个行为（或解答）的好坏，才能设计奖励信号驱动学习。若验证机制简单——比如对数值、布尔答案或代码输出进行快速自动化检测——就更易构造高效的 RL 环境。

“验证易难 ⇔ 学习易难”的映射

• Jason Wei 提出：“训练 AI 解决一个任务的难度，与该任务的可验证性成正比；所有既可解决又易于验证的任务，最终都会被 AI 掌握。”

• 可验证性要素包括：任务有明确的好坏标准，等价于 RL 中的清晰奖励定义; 单个解的验证耗时极短，对应 RL 中的低延迟奖励计算; 可同时验证大量解，对应批量化或并行奖励计算; 奖励与真实解质量高度相关，减少 RL 中的信号噪声。当这些条件满足时，RL 智能体能在多项式时间（经验上）收敛，任务也就“易学”——这正是将 NP 验证与 P 求解映射到现实中 AI 训练难度的关键。

相关研究现状

验证工程（Verification Engineering）

• VerIF 框架：Hao Peng等（2025）提出 VerIF，将规则化代码验证与基于大型推理模型（如 QwQ-32B）的 LLM 验证相结合，构建高质量的指令跟随验证集 VerInstruct，并显著提升 RLHF 性能arXiv。

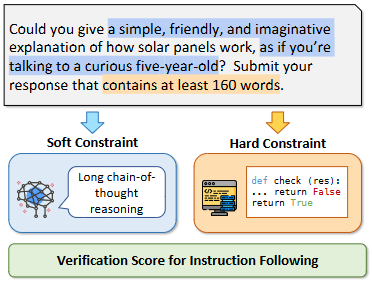
A simplified illustration of VERIF.

• LLM 借助“Chain-of-Thought”（CoT）或“Self-Critique”机制，对自身生成的解答进行多轮检查和修正，本质上是一种弱验证（weak verifier），并非严格的多项式时间保证，但有效提升了模型复杂推理能力stanford。同时，诸如“LLM as judge”研究，则探索如何让 LLM 充当 verifier，为开放式任务提供噪声奖励，但其信号不稳定、校准差，亟待形式化方法改进。

• VeriThinker（2025）通过专门的 CoT 验证任务微调推理模型，在压缩推理链条的同时保持准确率，展示了“专门训练验证器”对提高效率的巨大潜力arXiv。

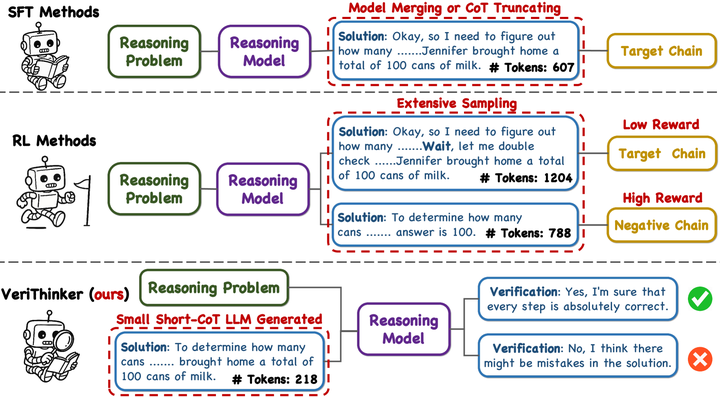
 VeriThinker 

可验证强化学习方法

• VIPER（Verifiable Policy Extraction）：Bastani 等（2018）通过从 DNN 策略抽取可验证的决策树，既保留性能又能借助现有形式化工具验证策略正确性，展现了“验证易构建 ⇔ 训练可控”的原理arXiv。

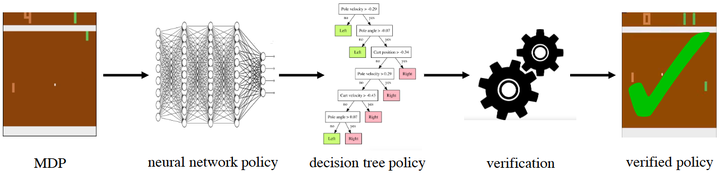
The high level approach VIPER uses to learn verifiable policies

• Shielding（安全 RL 屏蔽）：Alshiekh 等（2017）提出将“盾牌”集成到 RL 流程中，实时纠正可能违反安全规则的动作，强化了验证环节在训练与执行过程中的作用arXiv。

• Inductive Synthesis Framework：Zhu 等（2019）利用语法引导归纳合成，将复杂网络策略转化为可验证的程序，进一步拓展了 RL 可验证化的途径arXiv。

奖励模型与规范化

• RLHF 中的奖励模型构造：通过人类反馈训练奖励模型，使得模型行为更可预测、更易验证；该流程强调“验证信号质量”对最终性能影响之重维基百科。

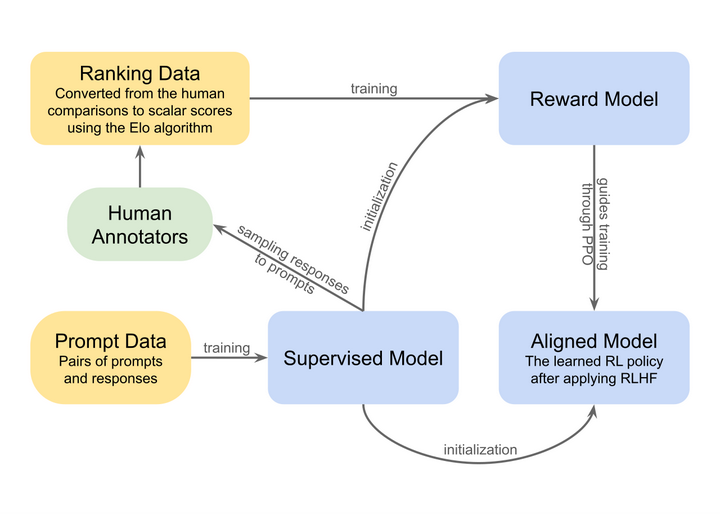
High-level overview of reinforcement learning from human feedback

• 奖励劫持（Reward hacking）：AI 可能找到验证漏洞，优化奖励却违背初衷——如“复制答案而非学习”，与验证噪声和可扩展性不足直接相关维基百科。

定理证明的方法（特殊问题）

• 多项式时间验证（如形式化定理证明器 Lean）在数学定理自动化证明中被用作 oracle verifiers，但仅适用于有限领域。为突破领域限制，研究者尝试将 RL 与符号推理结合：

• TRAIL（2019）将深度 RL 应用于一阶逻辑定理证明，在两个基准数据集上相较传统启发式方法解决了约15%更多定理arXiv。

• AlphaEvolve (2025) 并非仅依赖预先收集的数据集，而是根据自身在每一步生成的算法变体及其结果，动态调整“进化策略”，类似于 on‑policy RL 中通过当前策略采样来改进决策; 系统内置评估器（evaluators）对每个候选算法执行测试，反馈结果直接驱动下一代算法的生成，实现“生成→验证→生成”的闭环优化流程（arXiv）。

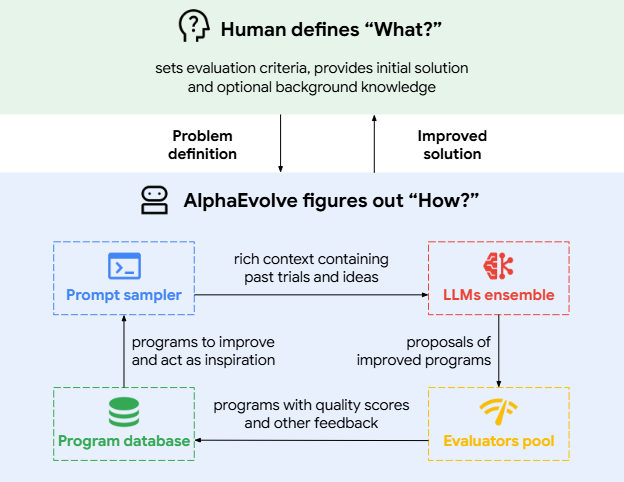
AlphaEvolve high-level overview

• Reinforcement Learning of Theorem Proving（2018）采用蒙特卡洛模拟与 RL，从大规模数学问题中学习推理策略，模型性能提升 40% 以上arXiv。

• JEPO（2025）提出 Jensen’s Evidence Lower Bound Policy Optimization，可在长序列输出（如数学证明）上进行 RL，而无需严格短期奖励匹配，弥补了对可验证数据的依赖arXiv。

JEPO canonical RL algorithm

PCP 定理视角：随机化验证的扩展

• PCP定理（Probabilistically Checkable Proofs Theorem）证明：每个 NP 问题都存在一个“概率可检验证明”，只需 O(log n) 随机比特和 O(1) 查询位数，即可完成多项式时间验证维基百科。

• PCP 框架可看作“随机化的 verifier”，其思想与 RL 中通过随机采样轨迹获取奖励信号有相通之处：都依赖对解答局部检查来全局评估正确性。当前研究尝试将 PCP 方法与 RL 奖励设计结合，以在更复杂任务中保持验证效率。

从“验证易难”角度看，PCP定理将NP中多项式时间验证的概念，提升为“只需常数查询和对数随机比特”的“超局部化”验证模式，为我们理解“验证越简单，任务越易学会”的Verifier’s Law提供了新的视角：即通过进一步降低验证的平均查询复杂度，RL环境设计与LLM自我验证或可获得更高效的学习与检验机制。

在RL环境与LLM自我验证中，Verifier’s Law 强调：奖励信号的可构造性（即“验证的易难”）直接影响任务的可学性。PCP定理展示了：即便原始验证需全局扫描，全局正确性依然可通过常数次局部检查高效完成。借鉴此思想，我们可以：

• 设计稀疏验证器：在RL中仅对轨迹中的关键状态或动作节点进行少量抽样评估，便能以高置信度判定整条轨迹质量；在LLM中仅对推理链的“关键步”进行自我校验，即可减少CoT长度，提高推理效率。

• 构造随机校验策略：引入对话式或多模态验证，让模型在不同随机子空间（如不同prompt扰动、不同知识片段）中抽查答案一致性，从而形成类似PCP的“随机查询”验证框架。

• 随机性奖励与gap检验：借鉴PCP的gap-introducing思想，RL环境可设计“带 gap 的奖励结构”，例如对于连续任务，引入阈值式奖励，使得模型若达到某一性能threshold，则获得高额奖励，否则微弱或零奖励，以加速模型突破性能临界。

• 近似验证与宽松健壮性：正如PCP从½ soundness 放大到任意ε，LLM自我验证可通过多轮bootstrap或ensemble验证，将初始验证信号的噪声减少至可接受水平，提升整体答案可靠度。

综上，Jason Wei 的 Verifier’s Law 以 RL 环境构造为切入，将 NP 验证复杂度映射为 AI 可学性的实践准则。当前研究从 LLM 自我验证、RL 定理证明到 JEPO 等算法，不断拓展从强验证到弱验证、不可验证场景下的学习能力，同时 PCP 理论提供的概率验证视角，也正在启发更高效的奖励设计。未来，结合形式化验证系统与 RL，将是进一步突破的关键。