动态规划算法

1. 动态规划算法与分治法类似，其基本思想也是将待求问题分解成若干个子问题。但是经分解得到的子问题往往不是互相独立的。有些子问题被重复计算了很多次。如果能够保存已解决的子问题的答案，而在需要时再找出已求得的答案，就可以避免重复计算。 

2. 矩阵连乘问题：

   // 第一行输入一个整数，表示有n个矩阵相乘 
   // 第二行输入n+1个整数，分别表示n个矩阵的行和列数
   // 输出最小的数乘次数
   #include<stdio.h>
   // m[i][j]表示将第i个矩阵到第j个矩阵相乘所需的最小乘法次数
   int m[11][11];// 下标为0的单元“不存储”有效数据
   int p[11];// 下标为0的单元“存储”有效数据
   void MatrixChain(int p[],int n)
   {
   	for(int i=1;i<=n;i++) m[i][i]=0;// 初始化第1条对角线
   	for(int r=2;r<=n;r++)// 解决规模为r的所有子问题 
   	{
   		for(int i=1;i<=n-r+1;i++)// 对于每个固定的r，有n-r+1种不同的起始位置 
   		{
   			int j = i + r - 1;// 确定右端点
   			m[i][j] = m[i][i] + m[i+1][j] + p[i-1]*p[i]*p[j]; 
   			for(int k=i; k<j; k++)// 控制不同的断开方式 
   			{
   				int q = m[i][k] + m[k+1][j] + p[i-1]*p[k]*p[j];
   				if (q < m[i][j]) m[i][j] = q;// 更新最小值
   			}
   		}
   	}
   }
   
   int main()
   {
   	int i,n;
   	scanf("%d",&n);
   	for(i=0;i<=n;i++)
   	{
   		scanf("%d",&p[i]);
   	}
   	MatrixChain(p,n);
   	printf("%d\n",m[1][n]);// 计算n个矩阵相乘所需的最小乘法次数
   	return 0;
   }

   

3. 动态规划算法的基本要素：（1）最优子结构：矩阵连乘计算次序问题的最优解包含着子问题的最优解。（2）重复子问题：再用递归算法自顶向下解决问题时，每次产生的子问题并不总是新问题，有些子问题被反复计算。
4. 最长公共子序列：

   // 第一行输入第一个子序列
   // 第二行输入第二个子序列
   // 第一行输出最长公共子序列的长度
   // 第二行输出最长公共子序列
   #include <stdio.h>
   #include <string.h>
   #define MAXLEN 81
   
   int b[MAXLEN][MAXLEN],c[MAXLEN][MAXLEN];// c是计算最优值时需要填写的二维表格，b是计算最优解时需要填写的二维表格
   
   void LCSLength(char x[], char y[], int m , int n) {
   	int i,j,k;
   	for(i=0; i<=n; i++)	c[0][i]=0;// 填写第0行数据
   	for(i=0; i<=m; i++)	c[i][0]=0;// 填写第0列数据
   	for(i=1; i<=m; i++) {// 分别填写第i行第j列对应的单元格数据
   		for(j=1; j<= n; j++) {
   			if(x[i]==y[j]) {
   				c[i][j] = c[i-1][j-1] + 1;
   				b[i][j] = 1;
   			} else if(c[i-1][j]>=c[i][j-1]) {
   				c[i][j] = c[i-1][j];
   				b[i][j] = 2;
   			} else {
   				c[i][j] = c[i][j-1];
   				b[i][j] = 3;
   			}
   		}
   	}
   }
   
   void LCS(char x[], int i, int j) {
   	if(i==0 || j==0) return;
   	if(b[i][j]==1) {
   		LCS(x,i-1,j-1);
   		printf("%c",x[i]);
   	} else if(b[i][j]==2) {
   		LCS(x,i-1,j);
   	} else {
   		LCS(x,i,j-1);
   	}
   }
   
   int main(void) {
   	char x[MAXLEN+1],y[MAXLEN+1];// 下标为0的单元不存放有效数据
   	int m,n;
   	scanf("%s",x);
   	m=strlen(x);
   	scanf("%s",y);
   	n=strlen(y);
   	// 将字符串x的内容从第一个字符开始复制到x的第二个字符位置
   	strcpy(x+1,x);// strcpy()函数用于将一个字符串复制到另一个位置
   	strcpy(y+1,y);// 字符串x和y中的字符分别向后移一位，目的是让0号单元不存放有效数据
   	LCSLength(x,y,m,n);
   	printf("%d\n",c[m][n]);// c[m][n]代表这两个字符串的最长公共子序列的长度
   	LCS(x,m,n);
   	return 0;
   } 

5. 0-1背包问题：

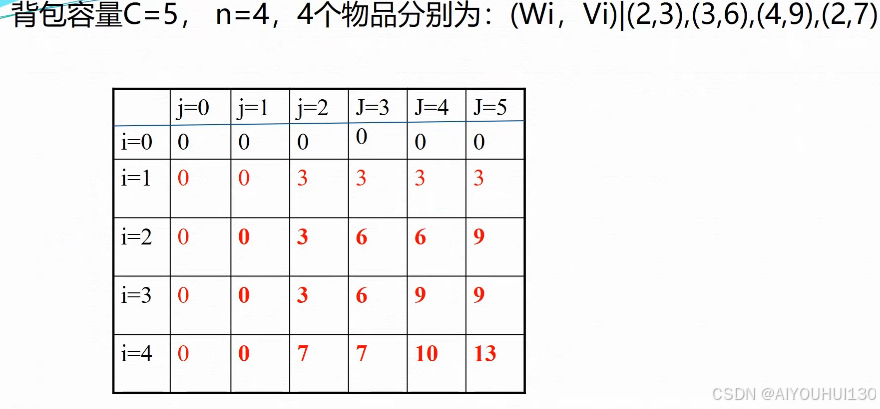
   // 第一行输出最大价值
   #include<stdio.h>
   // m[i][j]表示在考虑前i个物品，并且背包的容量为j时，可以获得的最大价值
   int m[11][21],w[11],v[11];// 第0行不存放有效数据
   
   int knapbag(int n, int c) {
   	for(int j=0; j<=c; j++){// 初始化动态规划表的第0行
   		m[0][j] = 0;
   	}
   	for(int i=1; i<=n; i++) {// 从第1个物品开始填表
   		for(int j=1;j<=c;j++) {// 对每个容量进行考虑
   			if(j<w[i]){
   				m[i][j] = m[i-1][j];// 不能放入该物品，最大价值等于不放该物品时的价值
   			} else {
   				m[i][j] = (m[i-1][j] > m[i-1][j-w[i]] + v[i]) ? m[i-1][j] : (m[i-1][j-w[i]] + v[i]);
   			}
   		}
   	}
   	return m[n][c];// 返回最大值
   }
   
   int main(void) {
   	int n,c,result;// 1<=n<=10; 0<c<=20
   	scanf("%d %d",&n,&c);
   	for (int i=1; i<=n; i++) scanf("%d",&w[i]);
   	for (int j=1; j<=n; j++) scanf("%d",&v[j]);
   	result=knapbag(n,c);
   	printf("%d\n",result);
   	return 0;
   }