o1推理无上限：集成CoT让Transformer解决P/poly类任意问题

作者：御坂美冰
原文：https://zhuanlan.zhihu.com/p/720520675

这篇文章主要探讨了“链式思维”（Chain of Thought, CoT）如何提升Transformer模型在处理复杂推理任务时的表达能力。其主要观点包括：

• • 链式思维：链式思维是指通过生成中间步骤来增强语言模型的推理能力。特别是在数学运算和符号推理任务中，链式思维被证明是有效的。传统的Transformer模型在没有足够的深度时，难以进行串行计算，而链式思维弥补了这一不足。

• • 理论分析：作者从计算复杂度的角度分析了Transformer模型的表达能力。通过构造布尔电路的类比，证明了在没有链式思维的情况下，固定深度的Transformer只能解决并行可计算的问题。但如果加入链式思维，Transformer可以解决需要串行计算的问题。这意味着通过生成足够多的推理步骤，Transformer能够处理复杂度更高的问题。

• • 链式思维的效果：作者通过实验验证了链式思维的有效性。文章选取了几类需要串行计算的问题，如置换群的组合、迭代平方和电路值问题。结果表明，启用链式思维后，即便是浅层的Transformer模型，也能够显著提升在这些任务上的表现。

• • 链式思维的复杂度类定义：定义了新的复杂度类CoT[T(n), d(n), s(n)]，用于描述使用链式思维的Transformer模型所能解决的问题。这一复杂度类明确了在不同的链式思维步数和嵌入维度下，模型的计算能力。

Paper:Chain of Thought Empowers Transformers to Solve Inherently Serial ProblemsAbs:https://arxiv.org/abs/2402.12875

1. 引言（Introduction）

该部分介绍了大型语言模型（LLM）在复杂推理任务（如数学问题求解和代码生成）方面表现出的卓越能力。文章指出，链式思维（CoT，Chain of Thought）通过生成中间推理步骤来增强这些模型的推理能力。虽然CoT的有效性在实践中已被证明，但其背后的机制尚未完全理解。本文通过理论和实验，分析了CoT如何赋予Transformer模型串行计算能力，这种能力是标准Transformer所不具备的。作者提出，CoT在增强模型的计算能力方面具有关键作用，特别是对于那些需要串行计算的问题。

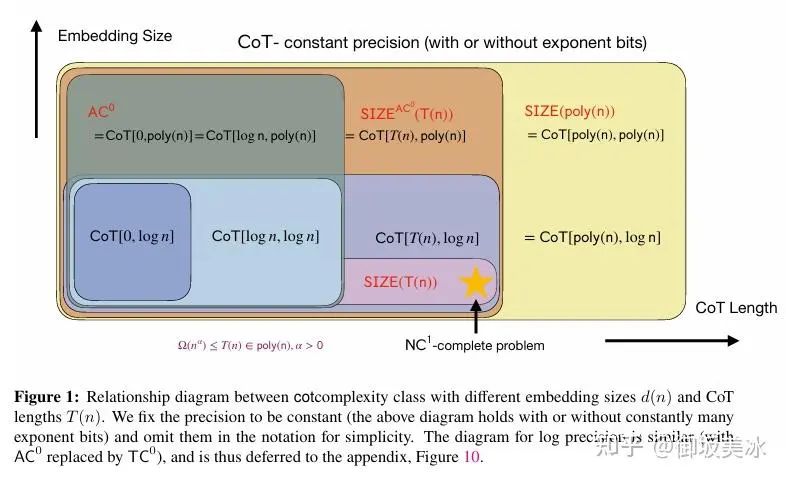
CoT复杂度类的关系图

这个图比较重要，详细介绍一下

• •  ：  是计算复杂度类，表示可以用常数深度的布尔电路解决的问题，这些电路的规模为多项式。它允许无穷多输入的AND和OR门，但不允许门限（多数表决）操作。AC^0类问题是非常简单的并行问题，比如判断所有输入是否全为1。

• • CoT[0, poly(n)]：表示没有链式思维（即CoT步数为0）且嵌入维度是多项式规模（poly(n)）的Transformer只能解决非常简单的并行计算任务，计算能力等同于 AC^0 。

• • CoT[logn, poly(n)]：表示链式思维长度为log(n)且嵌入维度是多项式规模的Transformer。虽然有一些链式思维步数，但由于嵌入维度较大，模型仍然只能处理 AC^0 类的简单并行问题。

：表示一个问题可以用规模为T(n)的 AC^0 电路解决。这种电路可以有效地处理简单的并行计算任务。

• • CoT[T(n), poly(n)]：表示链式思维长度为T(n)，嵌入维度为多项式规模的Transformer模型。链式思维的步数为T(n)，意味着模型可以通过逐步生成推理步骤来处理串行任务。但由于嵌入维度较大，它仍然在AC^0的范围内，适合解决并行问题。

• • SIZE(poly(n))：表示问题可以通过多项式规模的布尔电路来解决，且电路的深度没有限制。这意味着这些电路可以执行多步串行计算，因此可以解决P/poly类问题。P/poly类允许针对不同输入大小生成不同的电路，这使得它比AC^0和TC^0更强大。

• • CoT[poly(n), poly(n)]：表示链式思维长度和嵌入维度均为多项式规模的Transformer。这个模型能够通过逐步生成和处理复杂的推理步骤解决复杂问题，包括P/poly类问题。

• • CoT[poly(n), logn]：表示链式思维长度为多项式，但嵌入维度为log(n)的Transformer。虽然嵌入维度较小，但由于链式思维步数足够多，它可以处理与多项式规模电路相当的问题，因此同样可以解决P/poly类问题。

2. 符号和预备知识

该部分介绍了用于讨论Transformer模型的理论基础和符号。具体内容包括：