5.11.在线索二叉树中找前驱和后继

---

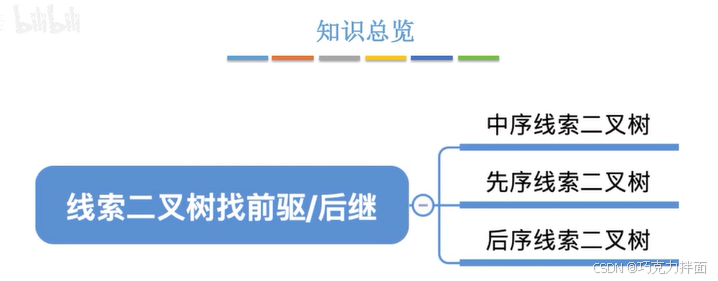
一.中序线索二叉树找中序后继：

中序线索二叉树中找指定结点的中序后继（注：此时的二叉树已经被线索化，而且是中序线索化）->

1.如果指定结点的右孩子指针已经被线索化：

p结点代表指定结点，如果指定结点的右孩子指针已经被线索化，那么指定结点的右孩子指针所指向的结点就是指定结点的中序后继，此时找指定结点的中序后继就会方便很多：

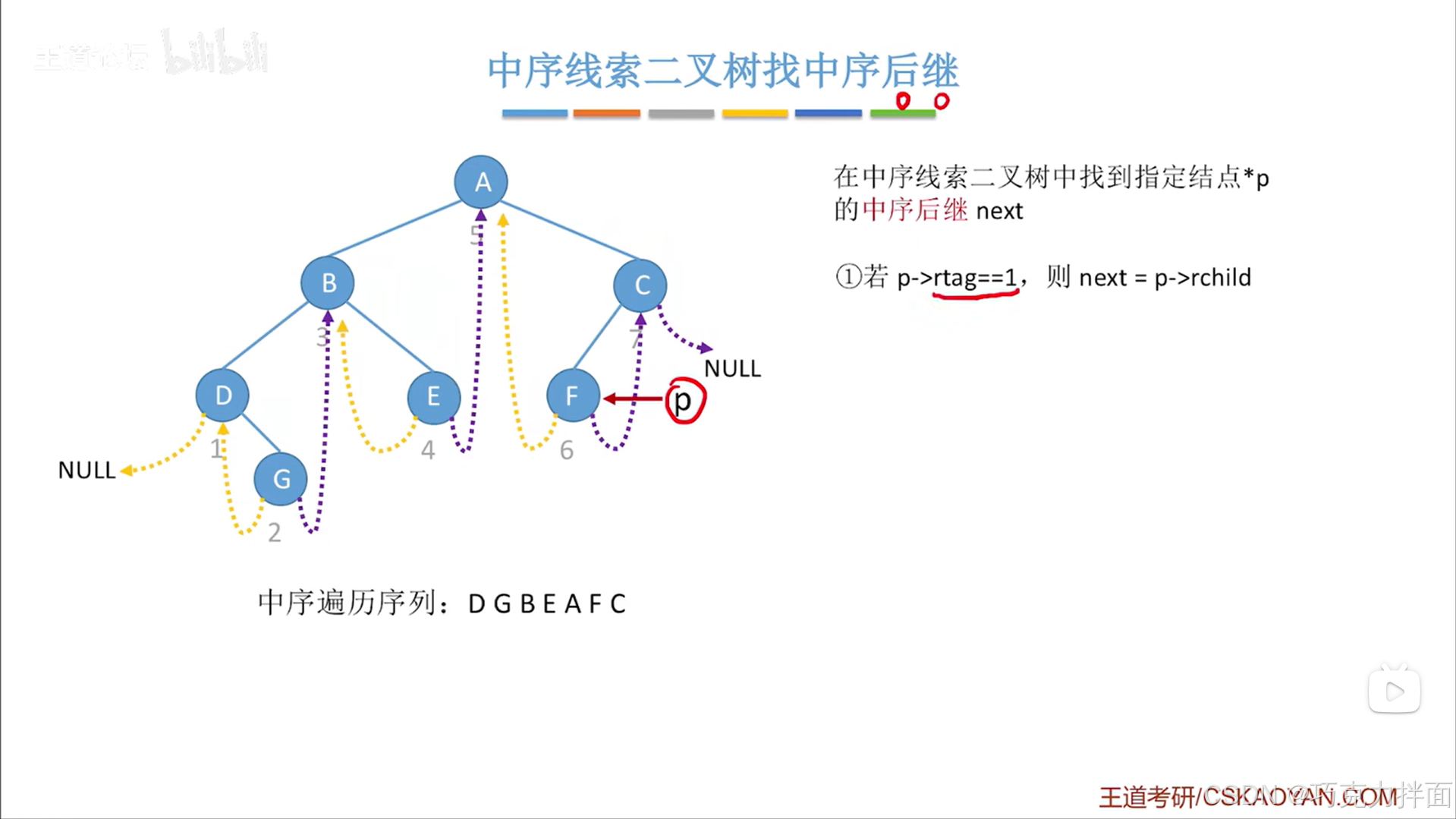
2.如果指定结点的右孩子指针还没有被线索化：

p结点代表指定结点，如果指定结点即p结点的右孩子指针并没有被线索化，那么就意味着该结点即p结点的右孩子指针指向一个结点即存在真正的右孩子（右子树非空），既然是找的中序后继即按照中序遍历来找一个结点的后继结点，中序遍历的访问顺序是左、根、右，现在已经知道指定结点即p结点有右孩子，所以按照中序遍历的规则，访问完当前结点即p结点后，需要再中序遍历右孩子，按照中序遍历的规则，在这个右子树中第一个被中序遍历的结点就是当前结点即p结点的后继结点，现在假设p结点只有一个右孩子，并且p结点的右孩子结点就是最终结点，也是叶子结点，显然这个右孩子结点就是p结点的后继结点：

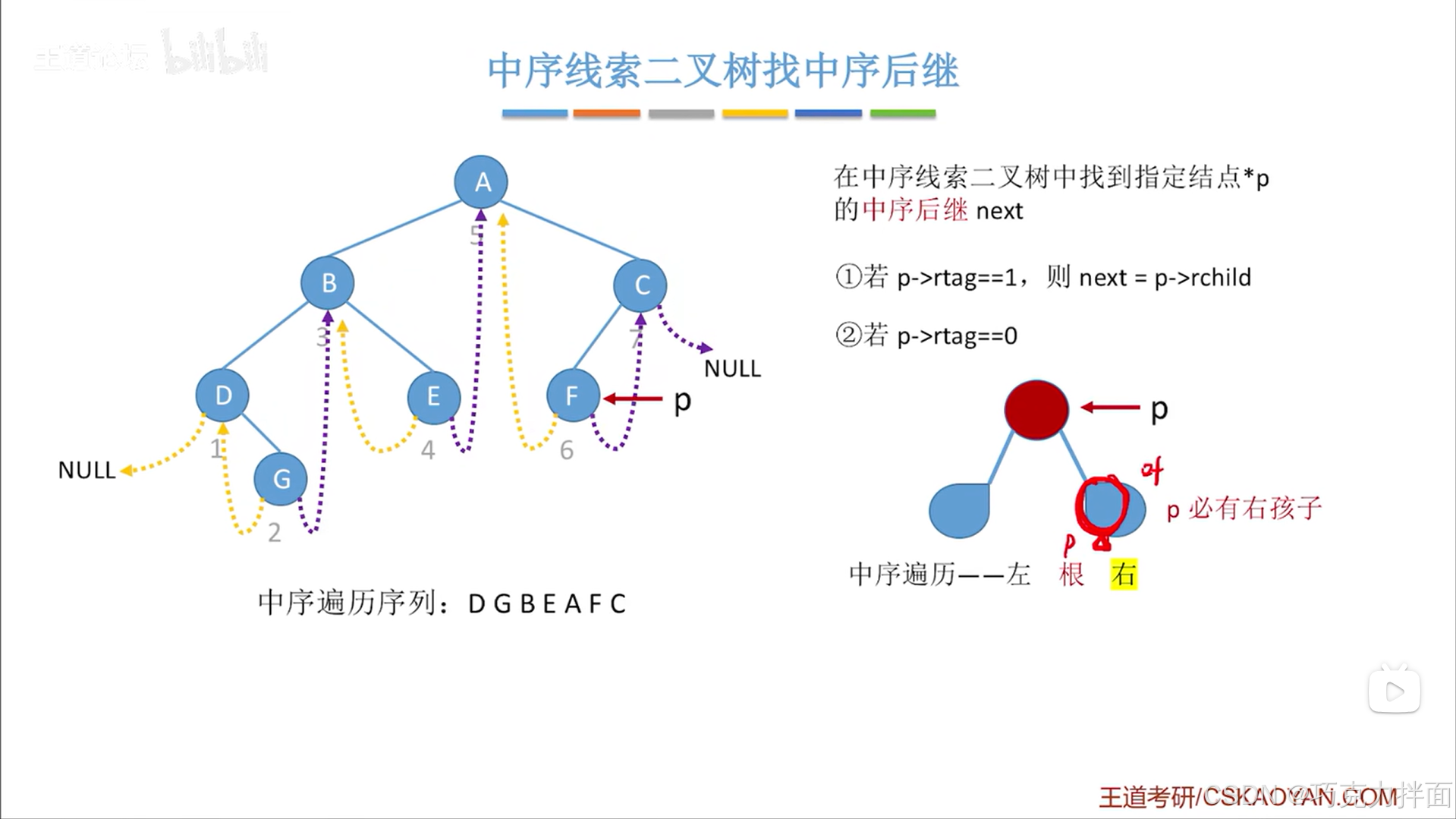
但如果假设p结点的右孩子结点并不是叶子结点即p结点的右孩子结点下还有左/右孩子结点，根据中序遍历访问顺序左、根、右的规则来遍历p结点的右子树，最左下角的结点就是p结点的右子树中最先被访问的结点即p结点之后第一个被访问的结点：

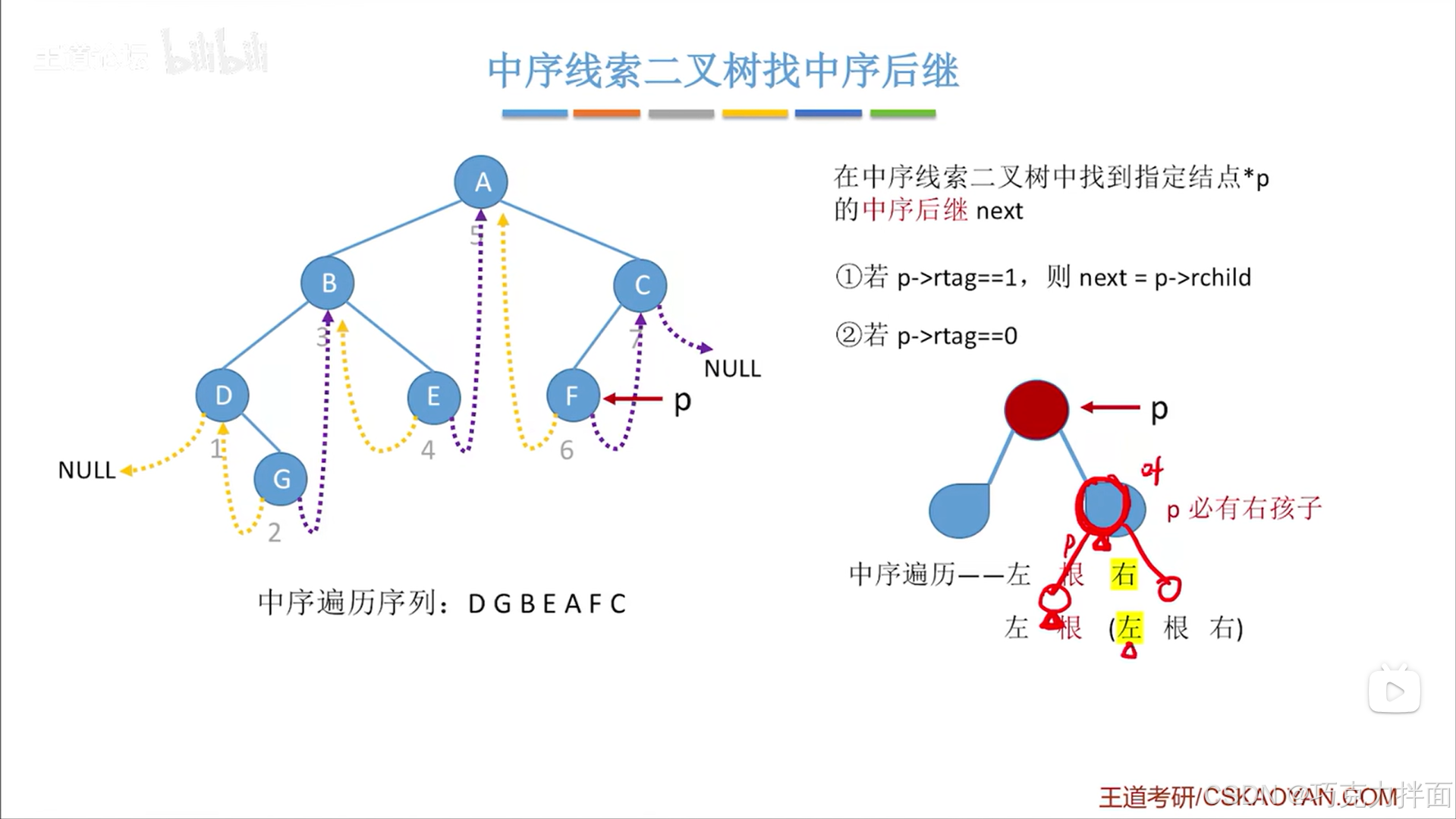
紧接着上述图片，如果继续增加结点如下述图片，可知最左下角的结点就是p结点的右子树中最先被访问的结点即p结点之后第一个被访问的结点：

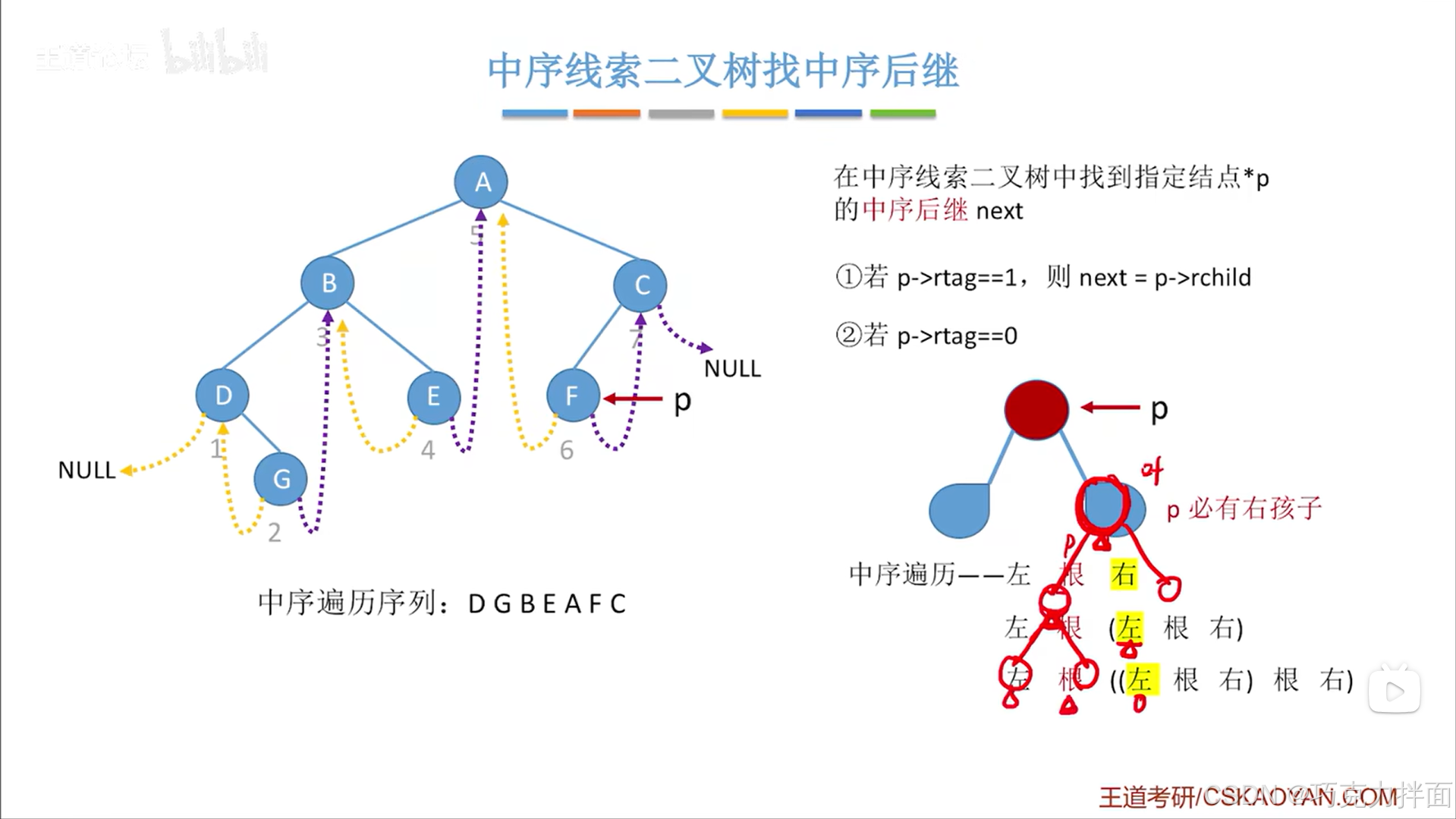
由此可知规律就是在中序线索二叉树找中序后继中p结点即当前结点的右子树当中最左下角的结点就是p结点即当前结点的后继结点：

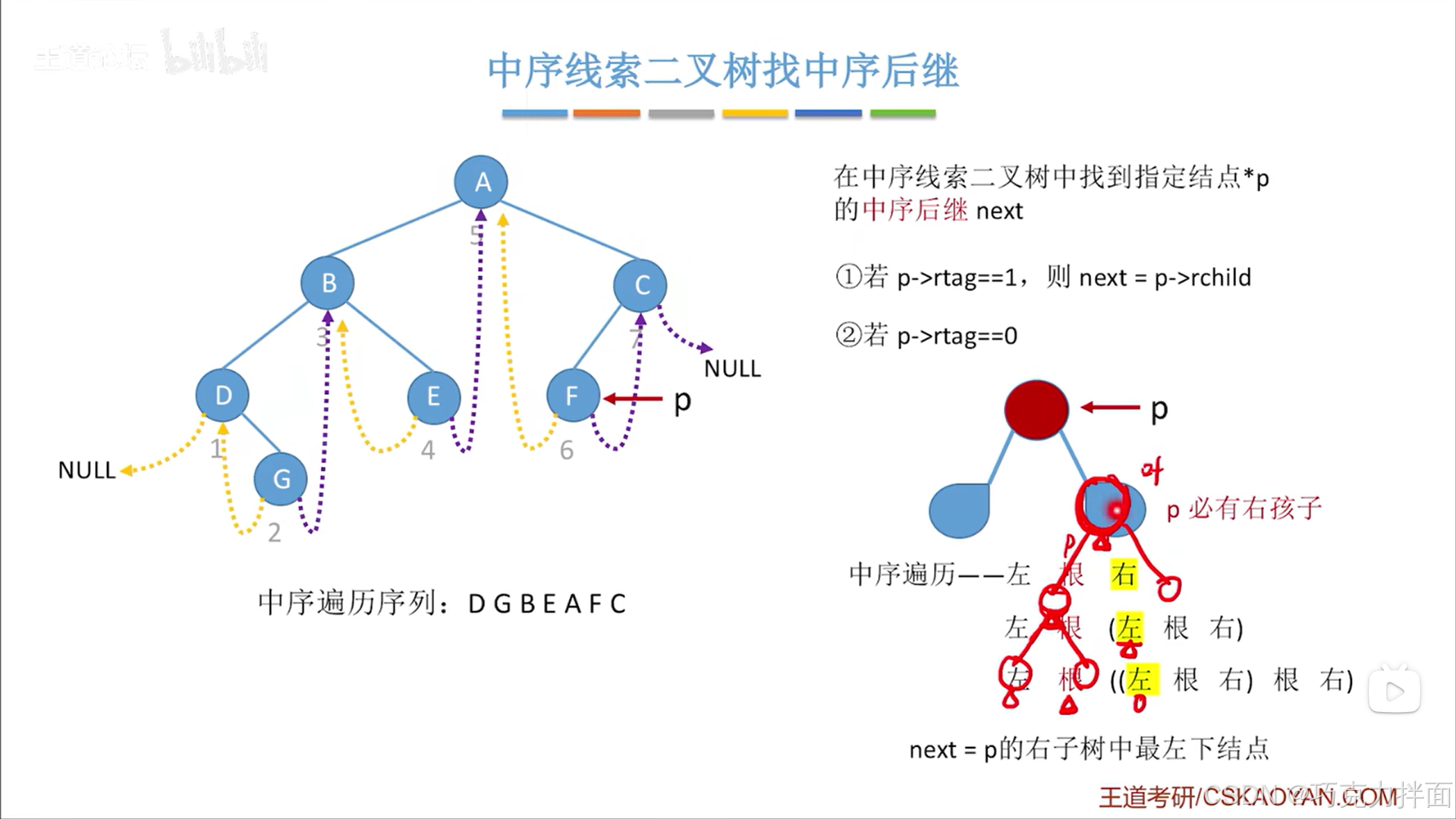
3.中序线索二叉树找中序后继的代码：

注：此时的二叉树已经被线索化

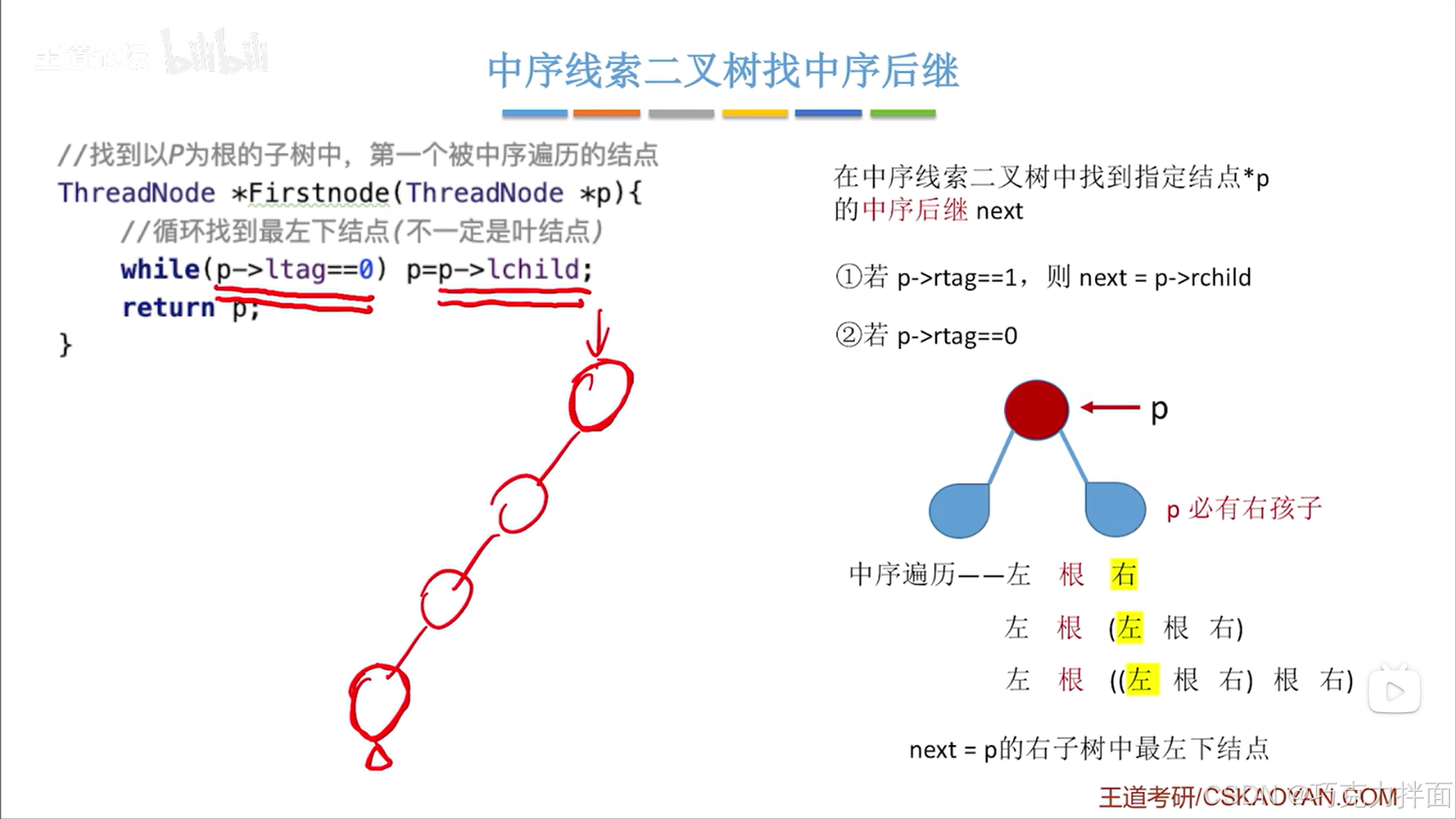
• ThreadNode是二叉树的结点类型，*p代表指定结点，ltag和rtag分别代表左线索标志和右线索标志，lchild和rchild分别代表左孩子指针和右孩子指针

• *Firstnode函数是用来找以指定结点p为根结点的左、右子树中，第一个被中序遍历的结点->首先要知道中序遍历的顺序是"左根右"，详情见"5.6.二叉树的先,中,后序遍历"，因此中序遍历到的第一个结点一定是在左子树中，因此要不断地往左子树上找->在函数体中，while函数的循环条件是如果指定结点的左线索标志为0即指定结点的左孩子指针没有被线索化，意味着存在左子树，于是开始不断的访问指定结点左孩子指针上的结点，并赋值为指定结点，之后继续判断是否循环，如果指定结点的左线索标志不为0时即被线索化，意味着不存在左子树了，跳出循环，最终找到最左下角的结点

• 二叉树进行中序遍历后可知最左下角的结点就是该二叉树被中序遍历后所访问的第一个结点

• *Firstnode函数的核心就是不断地往左子树上找，因为以p结点为根结点的左、右子树中，如果采用中序遍历，根据中序遍历的规则"左、根、右"可知第一个被中序遍历的结点一定在p结点的左子树上

• ThreadNode是二叉树的结点类型，*p代表指定结点，ltag和rtag分别代表左线索标志和右线索标志，lchild和rchild分别代表左孩子指针和右孩子指针

• *Nextnode函数是用来在中序线索二叉树中找到指定结点p的中序后继结点（中序后继就是指定节结点的右子树上的结点）->在函数体中如果指定结点p的右线索标志为0即指定结点p的右孩子指针没有被线索化，意味着存在右子树，就调用Firstnode函数，其中把指定结点p的右子树传入Firstnode函数，最终就可以找到指定结点p的右子树中最左下角的结点（也就是找到指定结点的右子树中第一个被中序遍历的结点）即指定结点p的后继结点；如果不满足if条件，代表此时指定结点p的右线索标志为1，意味着p结点的右孩子指针被线索化，直接返回p结点的右孩子指针所指向的结点即后继线索(也就是p结点在遍历序列中下一个被访问的结点，详情见"5.10.二叉树的线索化"中的"中序线索化实例")

• *Nextnode函数核心就是如果指定结点p有右子树，就在右子树中找第一个被中序遍历的结点（找到的第一个被中序遍历