一.用土办法找到中序前驱:再次中序遍历二叉树,在这个过程中用一个变量记录当前结点的前驱结点
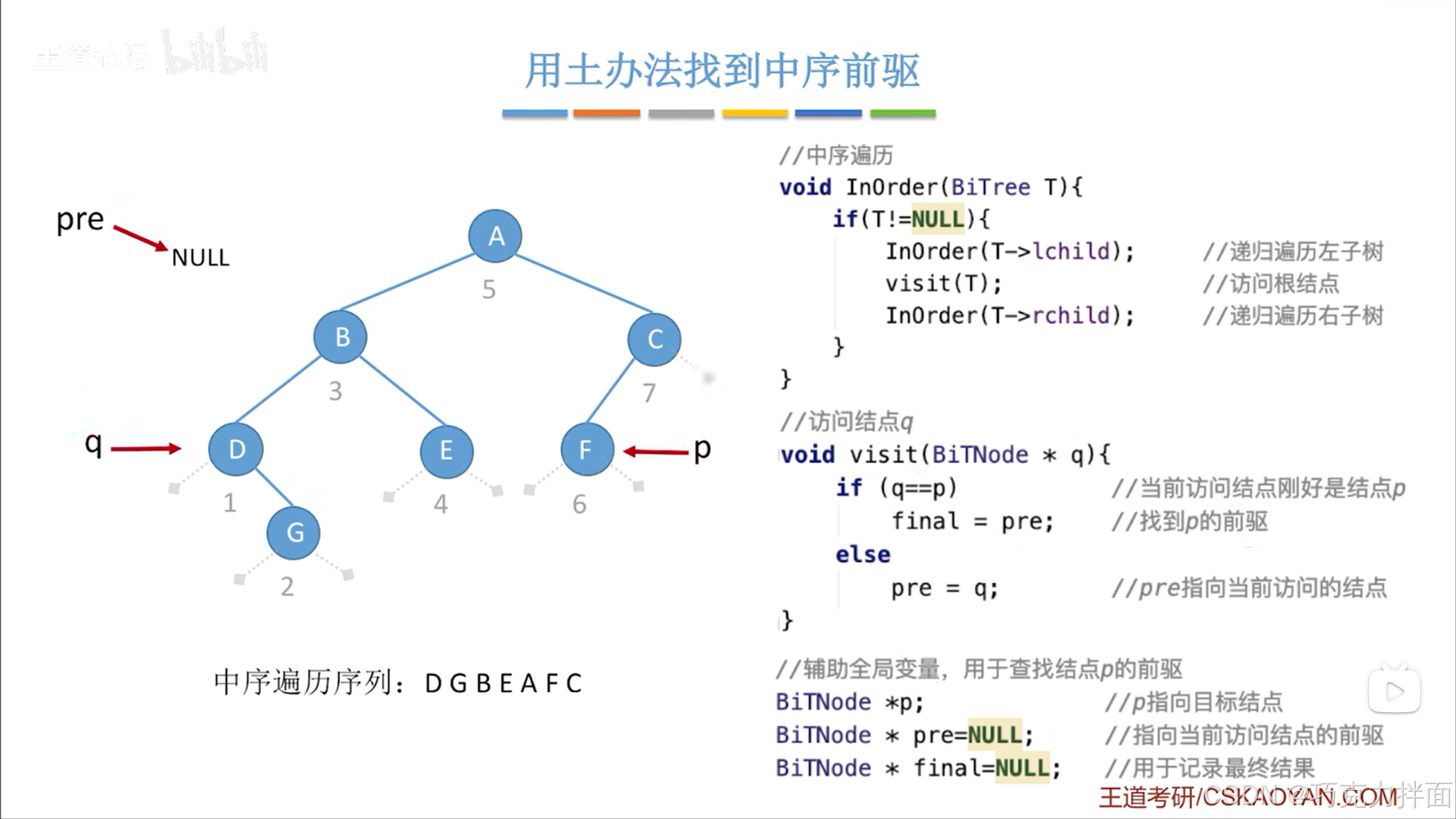
1.上述图片中用于中序遍历的InOrder函数的运行结果就是按照中序遍历序列DGBEAFC去访问各个结点;
2.InOrder函数的形参BiTree T是二叉树,T一开始代表根结点,T->lchild代表指向左子树,T->rchild代表指向右子树;
3.第一次运行InOrder函数时T代表二叉树的头结点A;每调用一次InOrder函数就可能有一次递归;
4.注:当T等于NULL或者执行完InOrder(T->rchild)后InOrder函数才会结束即只有当T等于NULL或者执行完InOrder(T->rchild)这层递归才算结束;而且函数中操作的变量属于局部变量,函数结束后变量就会恢复到调用该函数前的值,例如当T为A结点时调用InOrder(T->rchild),此时T->rchild为B结点,当InOrder(T->rchild)调用结束后,T仍为A结点;
5.对上述二叉树进行中序遍历演示:

5.本例中的visit函数是用来找指定结点的前驱结点,visit函数核心就是如果q指向的结点即当前结点不等于p指向的结点即目标结点的话,就把q指向的结点赋值给pre指向的结点
6.本例让目标结点为F结点即p指向F结点,而且p属于全局变量;q指向当前被访问的结点;pre指针指向q结点的前驱结点
利用中序遍历,第一个被访问的结点为D结点即一开始q指向D,而D结点的前驱为NULL即pre指向NULL,调用visit函数后发现此时q指向的结点(D结点)和p指向的结点(F结点)不相等,所以修改前驱结点为当前结点(D结点),当前结点(D结点)无需修改为下一个结点(G结点),因为递归过程就包含了把当前结点修改为访问下一个结点:
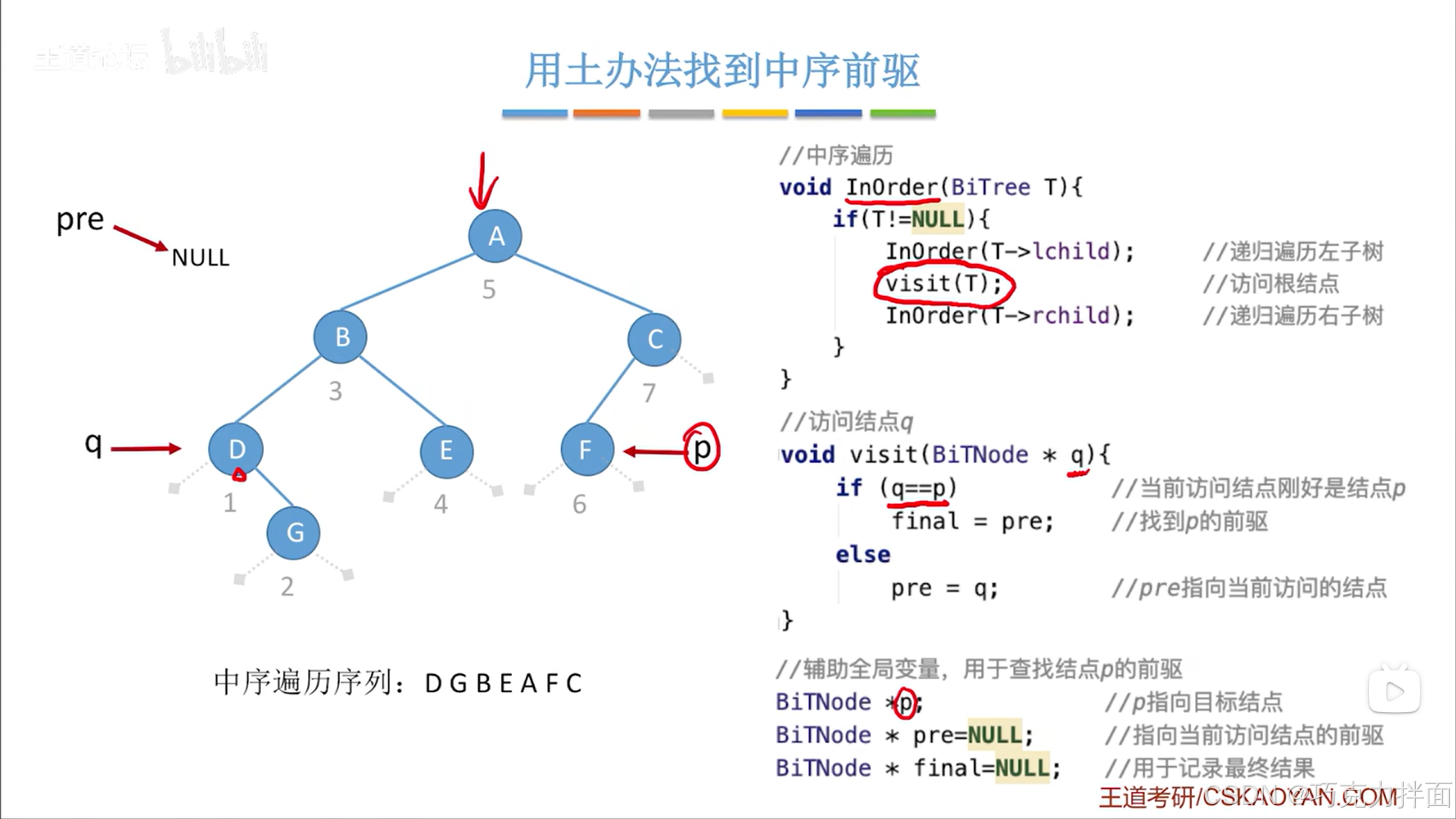

同理,第二个被访问的结点为G结点即q指向G结点,而G结点的前驱为D结点即pre指向D结点,调用visit函数后发现此时q指向的结点(G结点)和p指向的结点(F结点)不相等,所以修改前驱结点为当前结点(G结点),当前结点(G结点)无需修改为下一个结点(B结点),因为递归过程就包含了把当前结点修改为访问下一个结点:
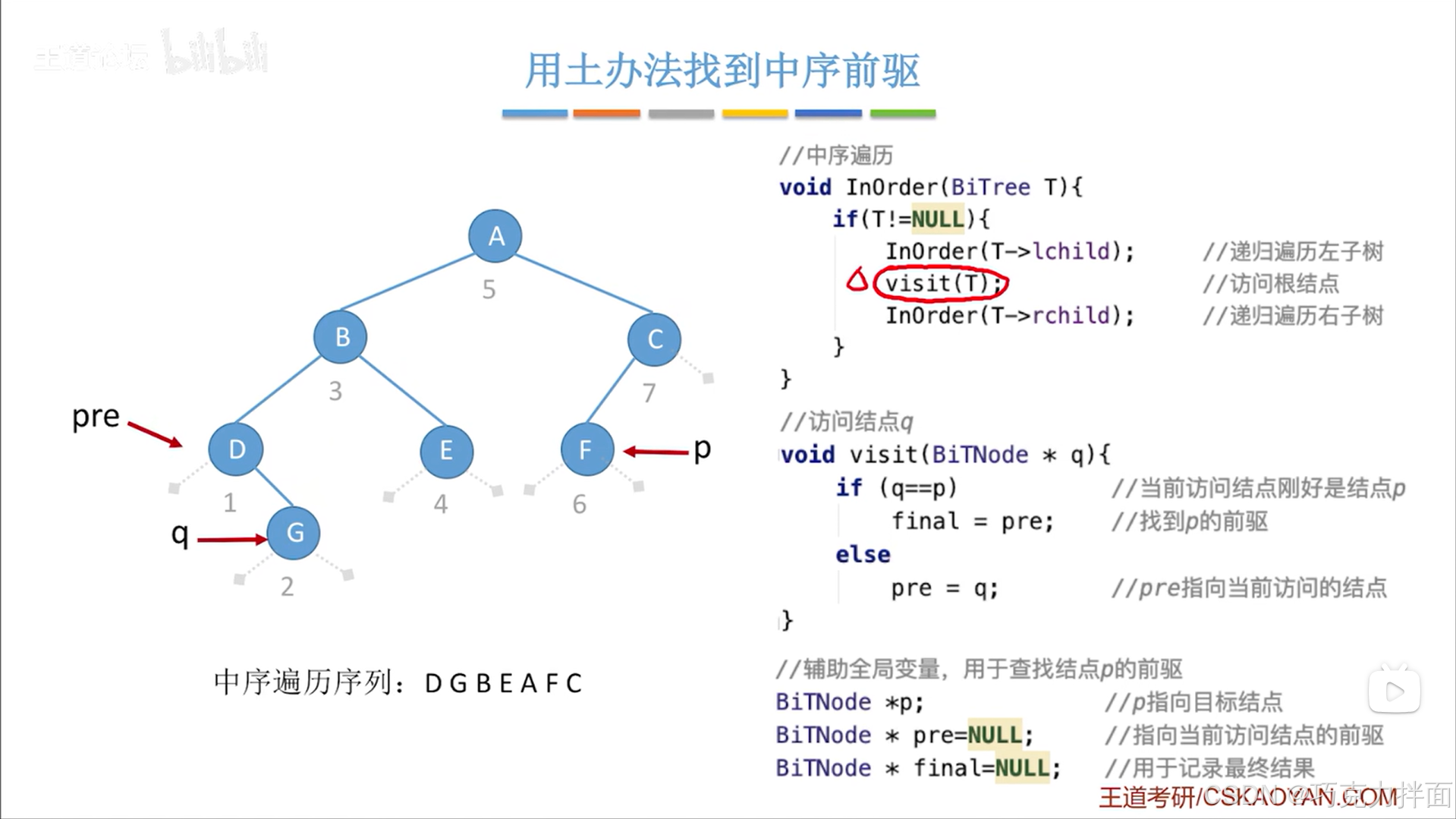
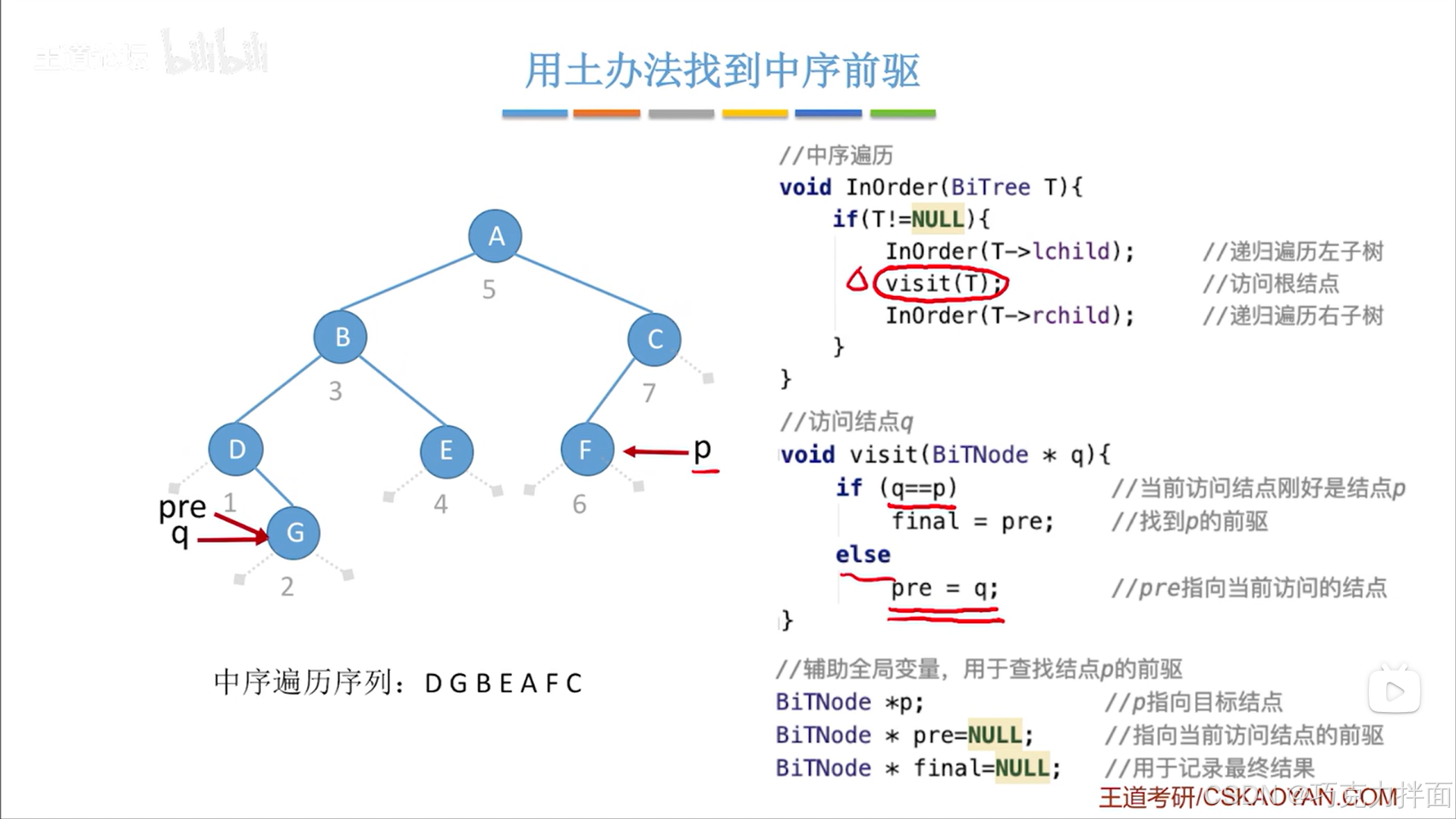
当前结点为第三个结点即B结点时:
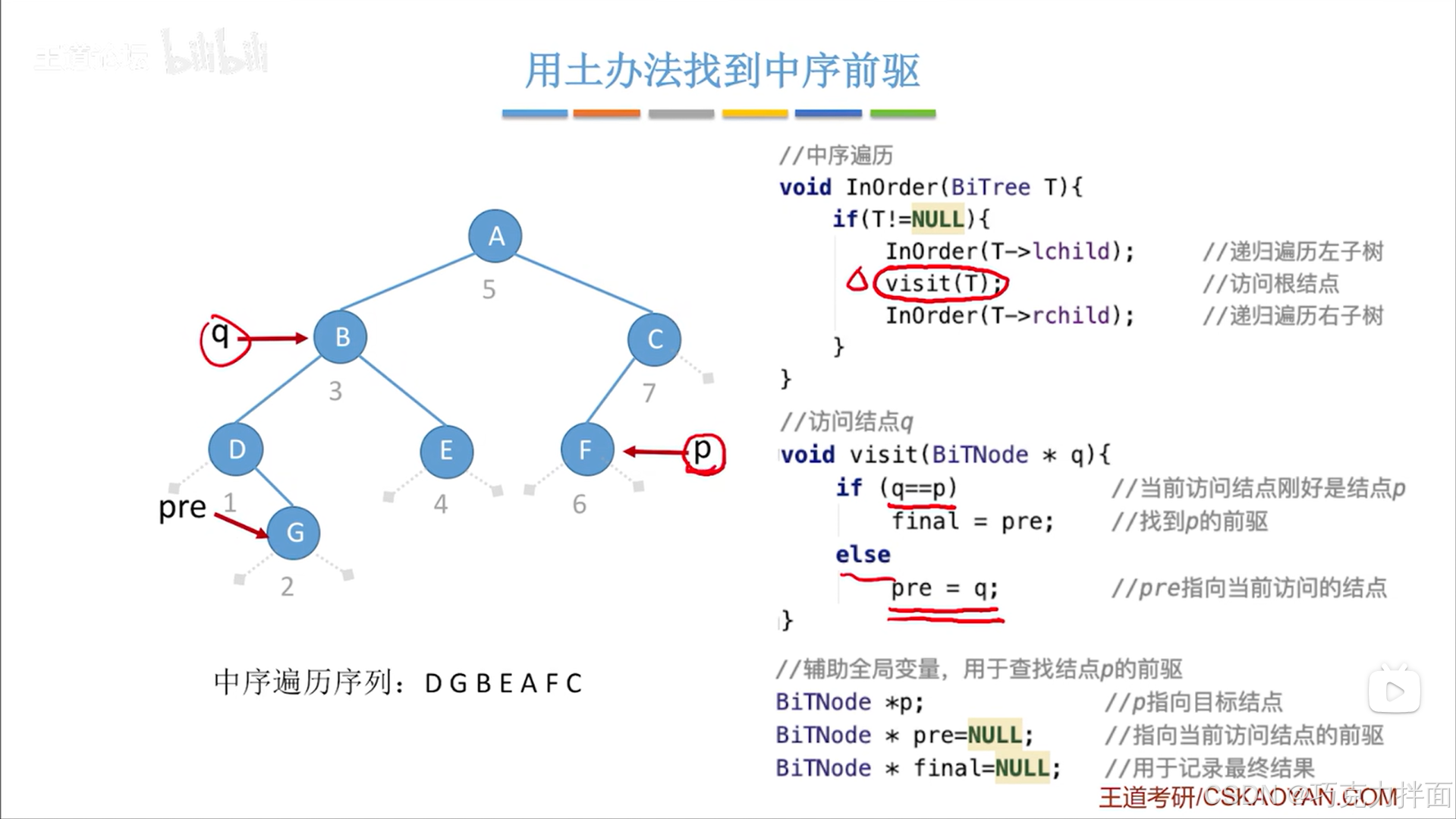
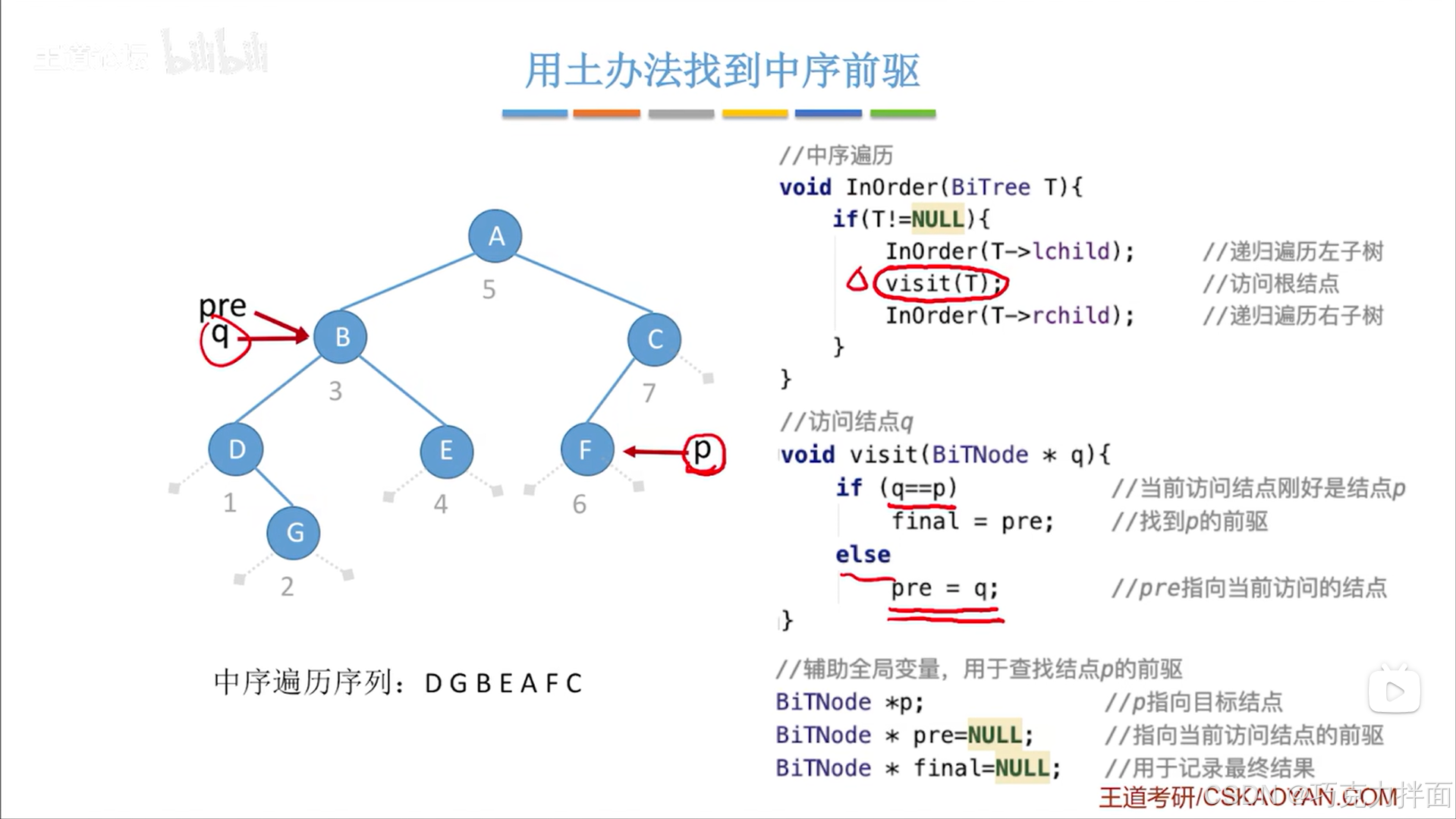
当前结点为第四个结点即E结点时:
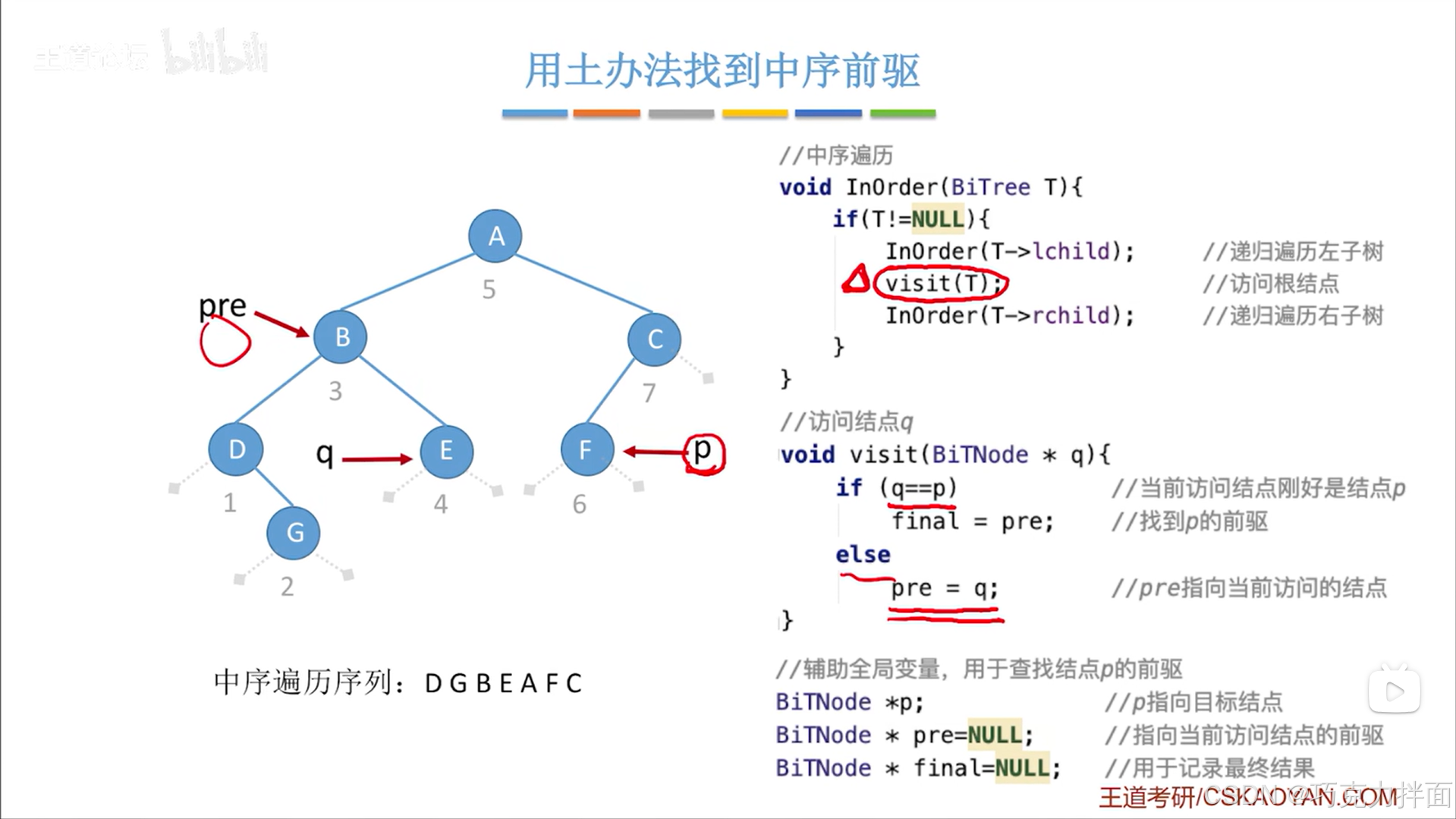
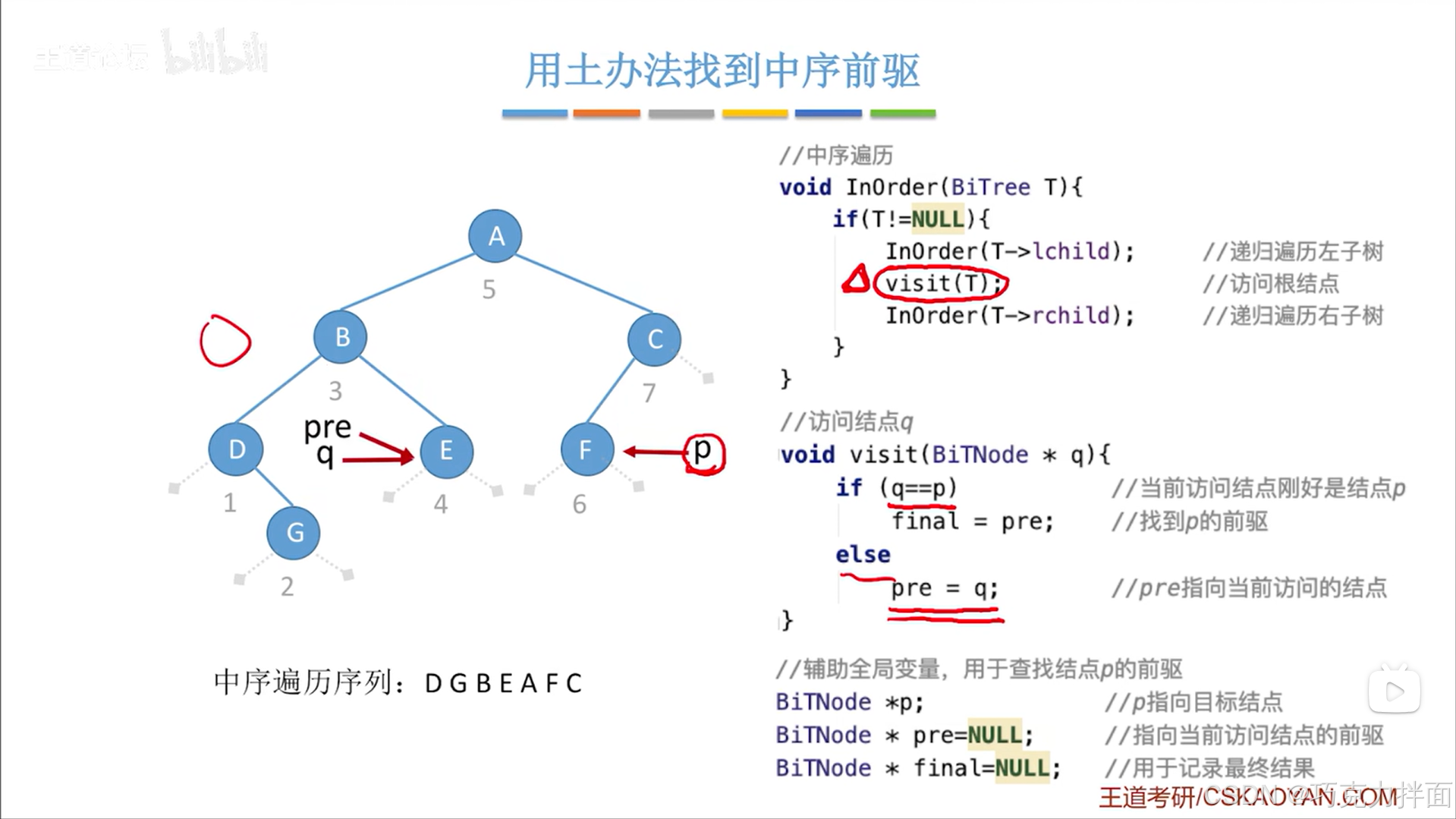
当前结点为第五个结点即A结点时:
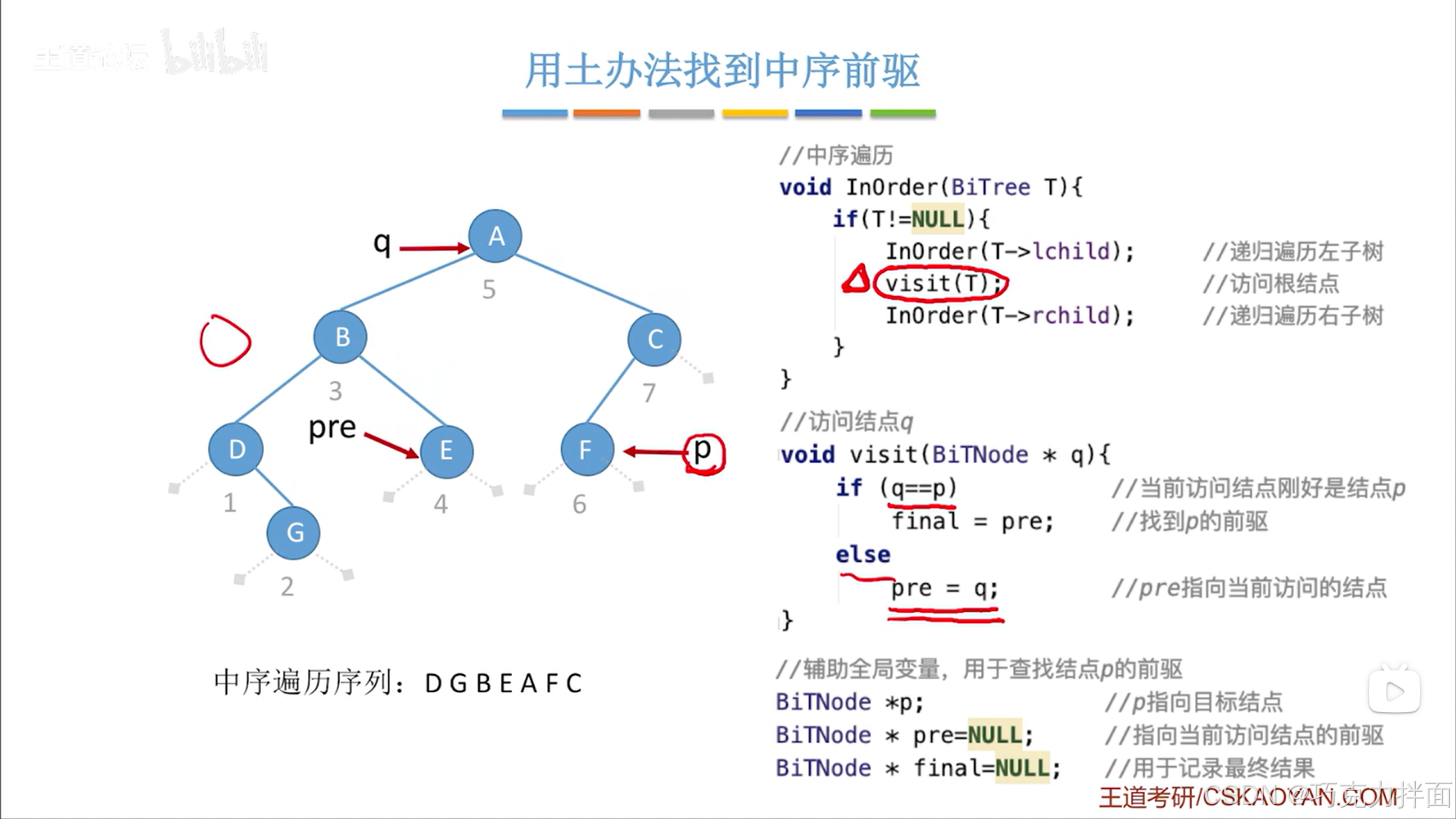
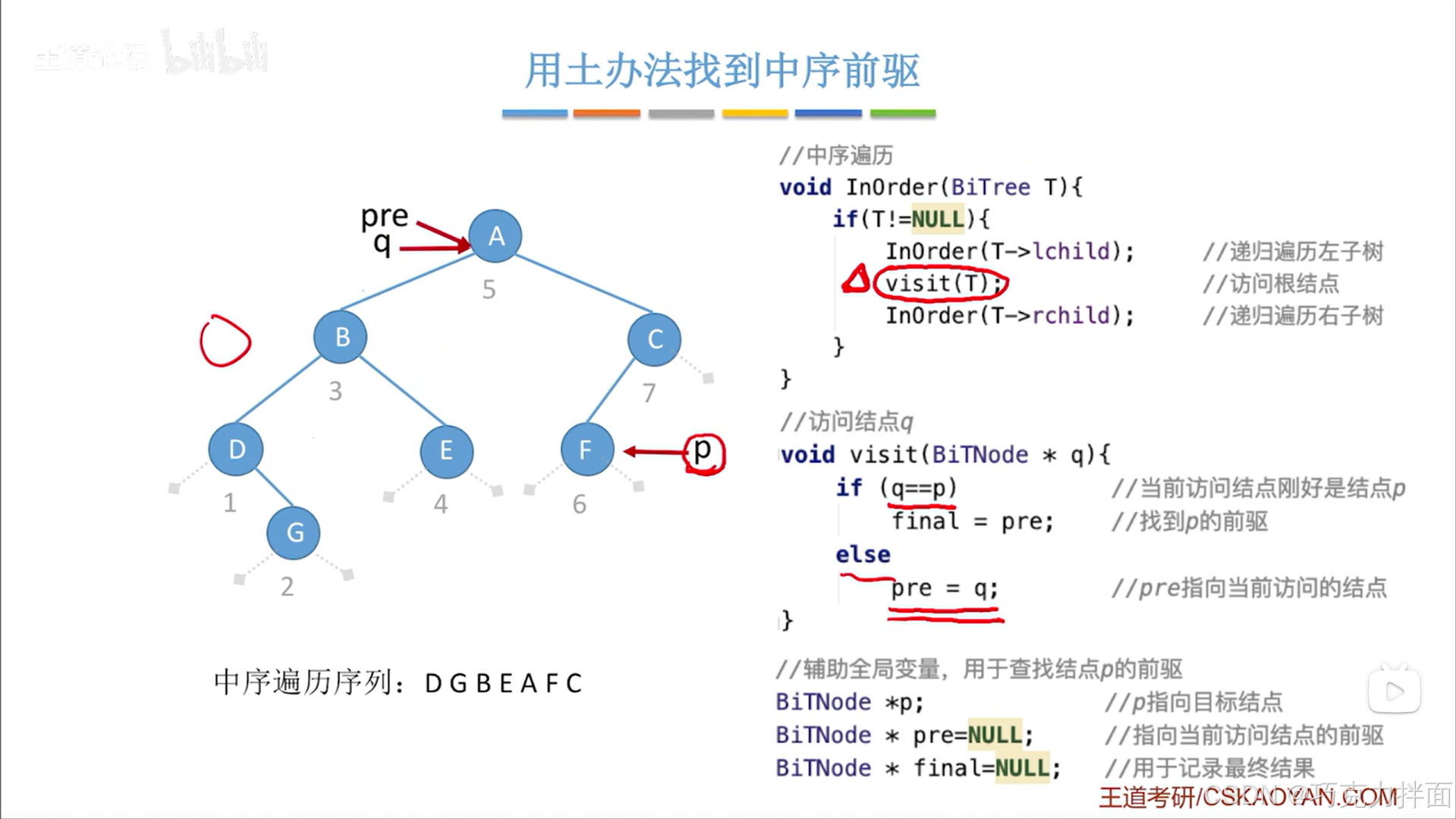
当前结点为第六个结点即F结点时:
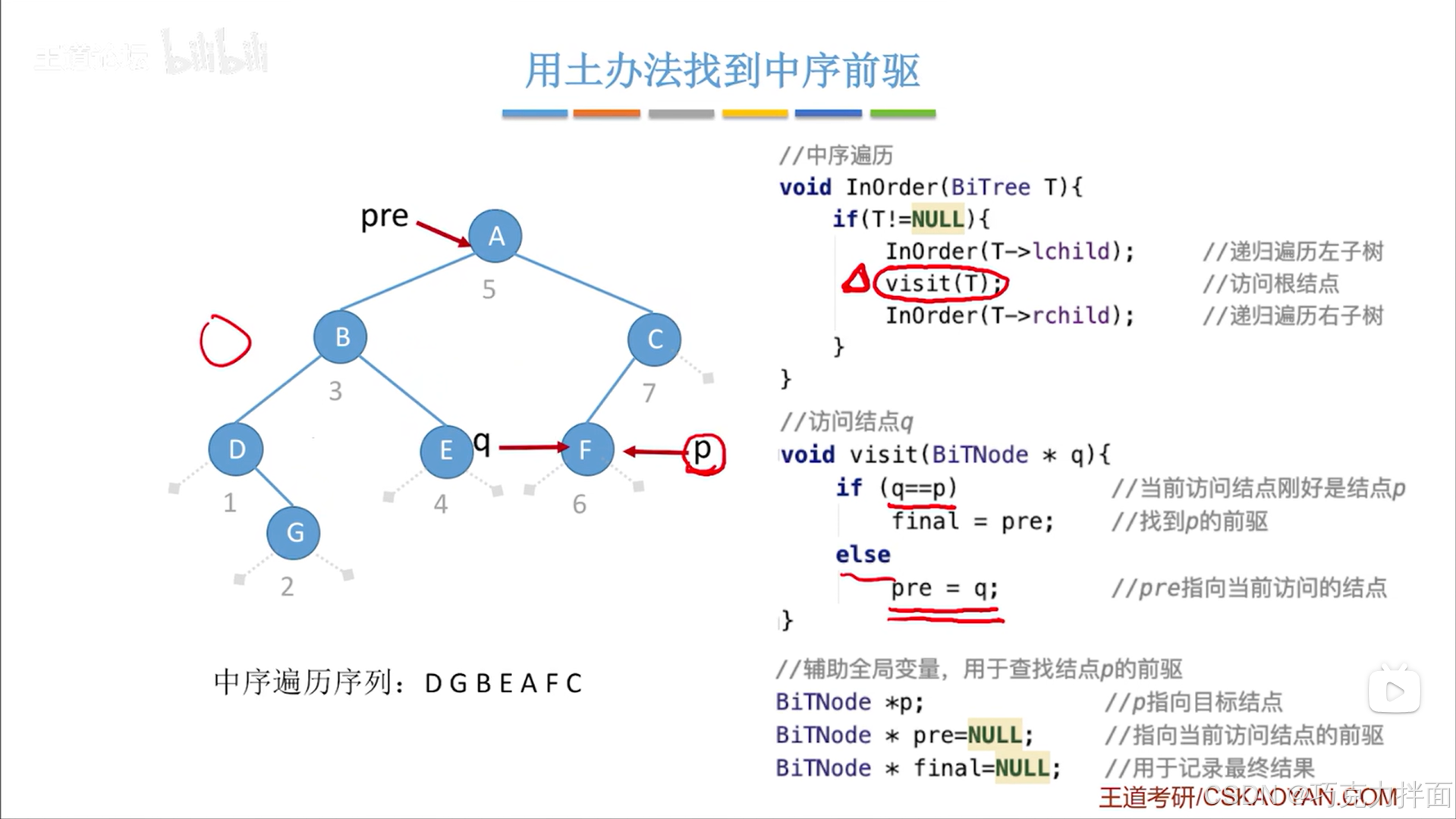
此时q所指的结点等于p结点,说明找到了目标结点,由于pre指针指向目标结点的前驱结点,那么F结点的前驱结点为A结点,最终用一个全局变量final记录找到的这个前驱结点即pre指向的结点:
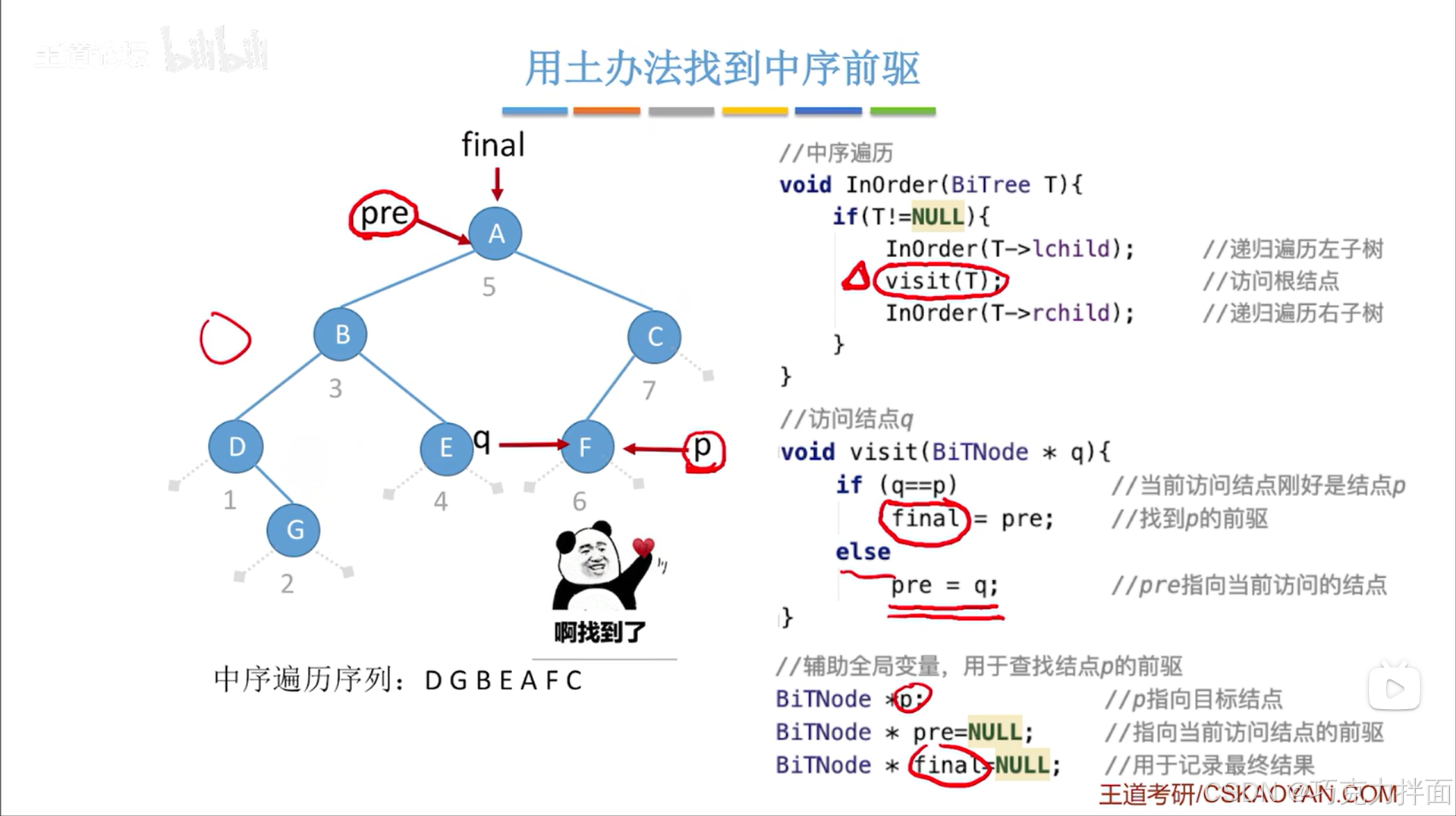
上述过程是找到了一个结点的中序前驱,因为是按照中序遍历的顺序来访问各个结点的,
由于这个过程是在找前驱结点,所以可以把InOrder函数名改为findPre更直观一些:
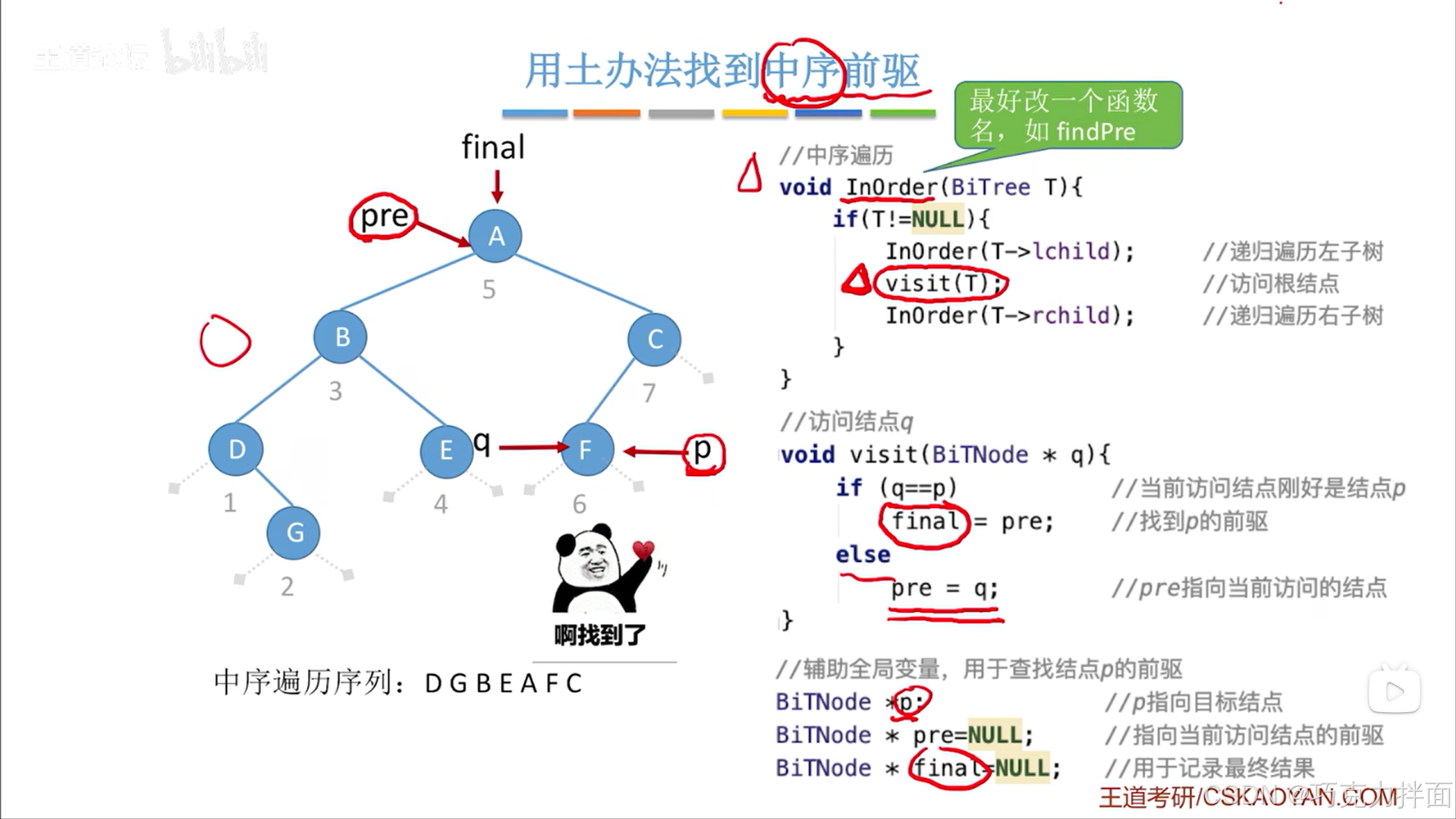
二.二叉树的线索化:
1.关键:
当对二叉树中的某一个结点进行线索化时,其实就是把这个结点的左孩子指针连上它的前驱结点,右孩子指针连上它的后继结点
2.中序线索化准备工作:
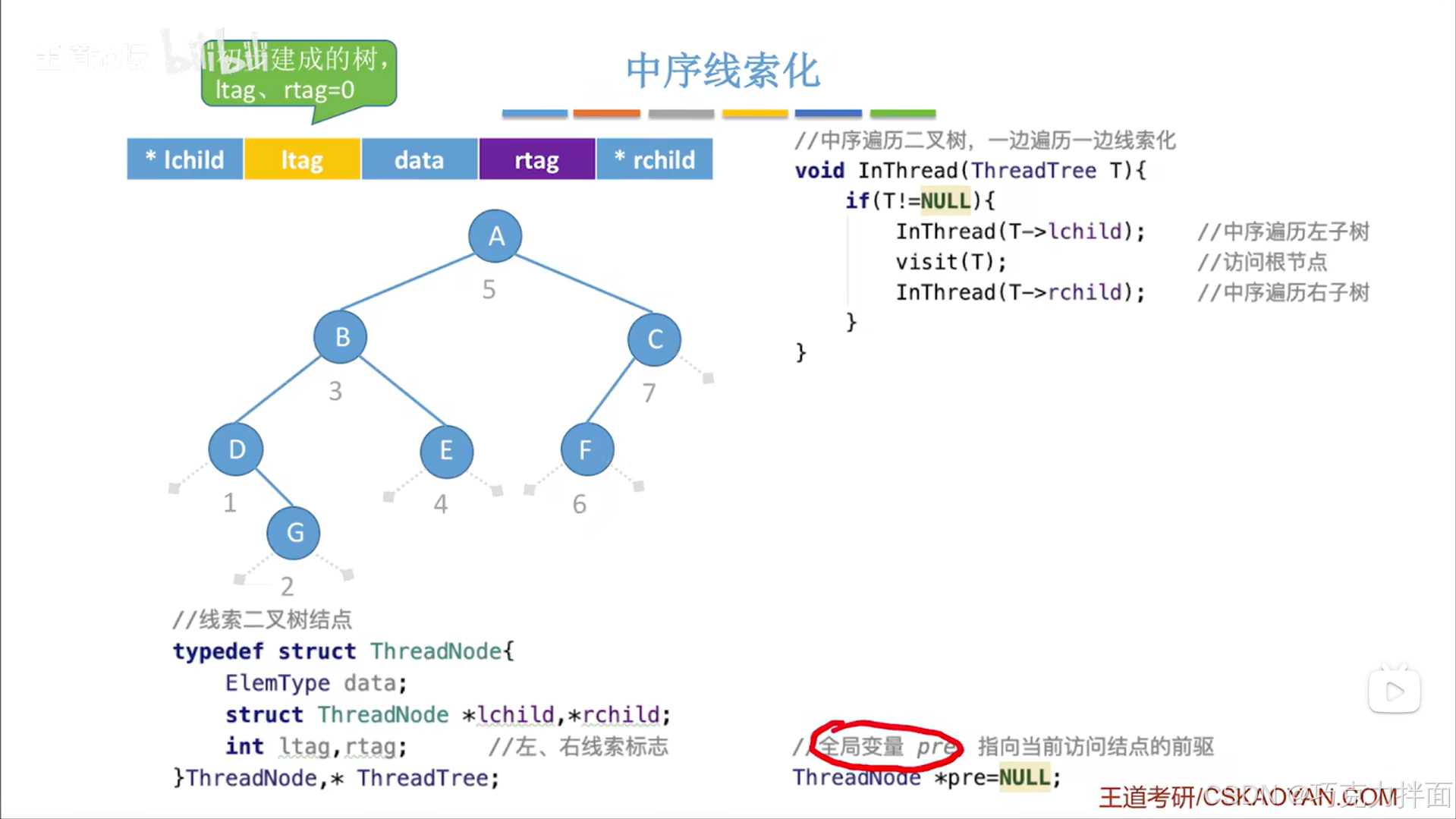
-
利用中序遍历后会得出二叉树中结点的中序遍历序列,在这个序列中(不是二叉树中)第一个结点索引为1,第二个结点索引为2,以此类推->ltag和rtag都指向的是结点的索引,而不是结点的值,如果ltag或rtag此时指向结点的索引,那么ltag或rtag的值就不能为0,如果为0说明此时没有指向结点的索引,先序遍历二叉树和后序遍历二叉树同理
-
假设已经初步建成一个二叉树,初步建成的二叉树中的ltag和rtag都会赋值为0,赋值为0的意思是ltag和rtag分别指向的是结点的左孩子和右孩子即没有指向结点的索引,也就是并没有被线索化
3.中序线索化实例:
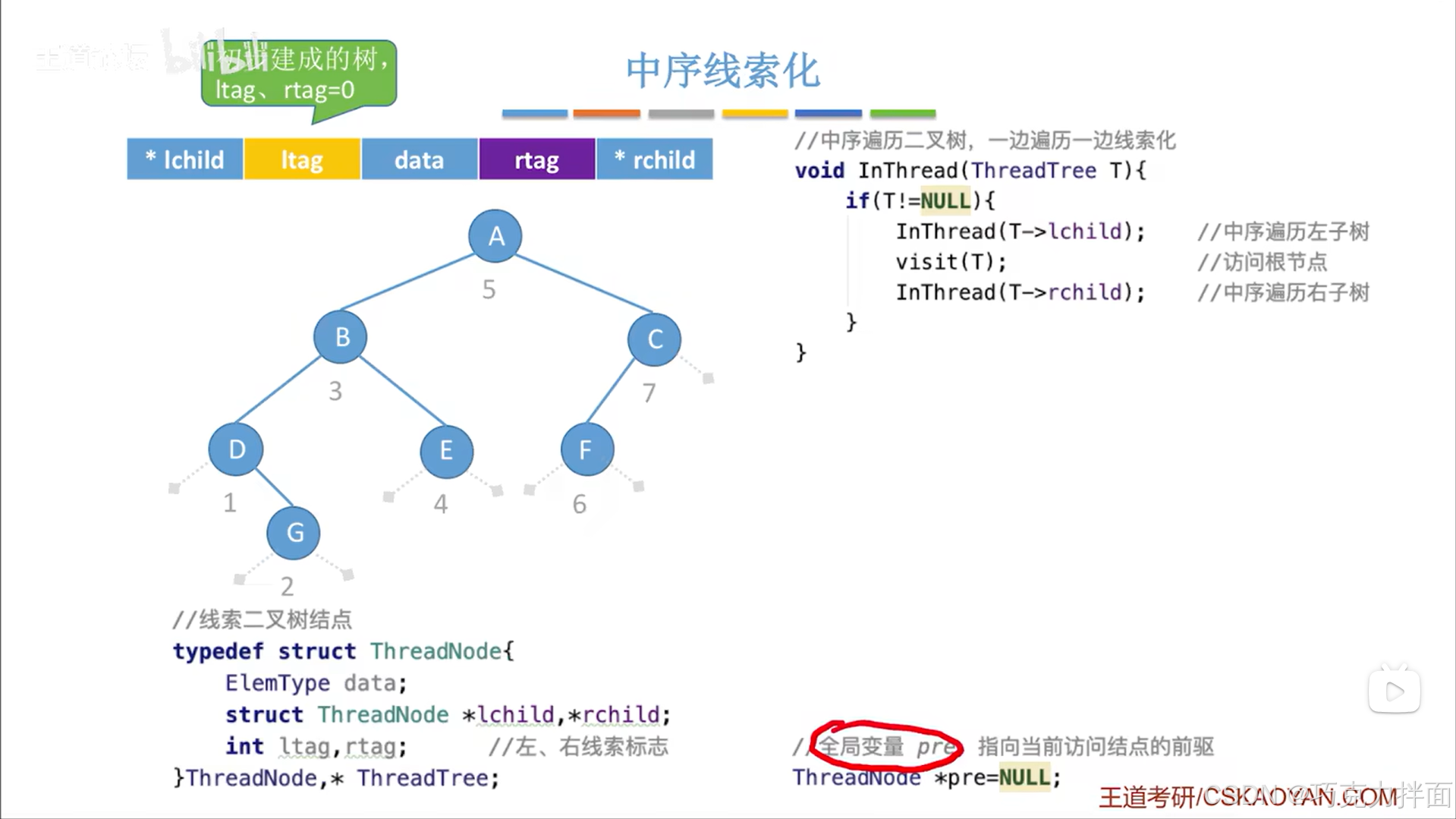
按照中序遍历规则,上述图片中的二叉树里的结点被访问的顺序为DGBEAFC。q结点为当前访问的结点。
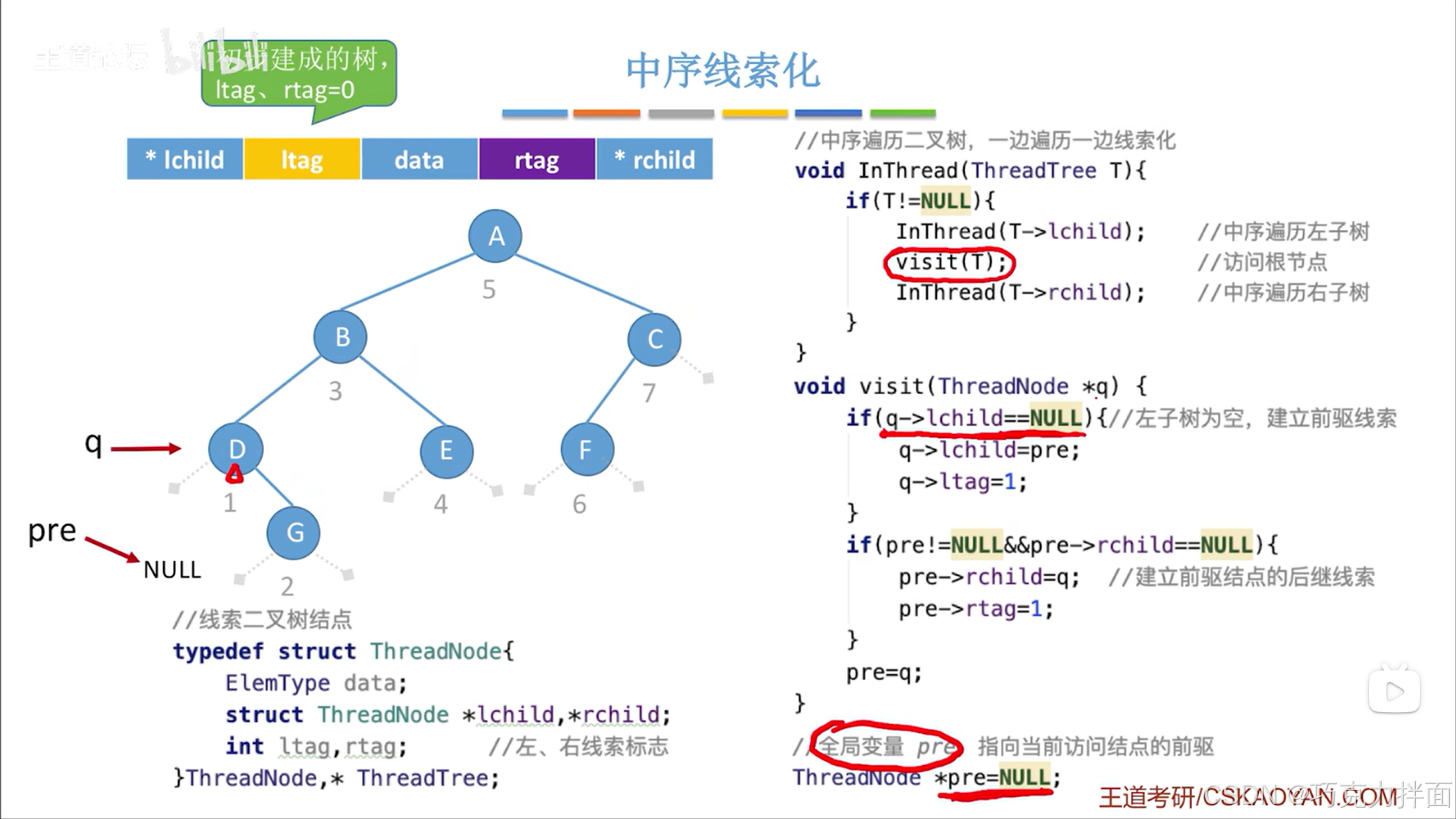
第一个被访问的结点为D结点,由于第一个结点没有前驱,所以此时指针pre指向NULL;从图中可知,D结点没有左孩子,所以要把该结点的左孩子指针线索化,这个事情就可以调用visit函数解决,就是visit函数里的第一个if语句,如果当前结点的左孩子为空的话,就应该把它的左孩子指针指向该结点的前驱,还需要修改左线索标志ltag的值为1(因为只有ltag或rtag等于1时才表示与之对应的孩子指针为线索):
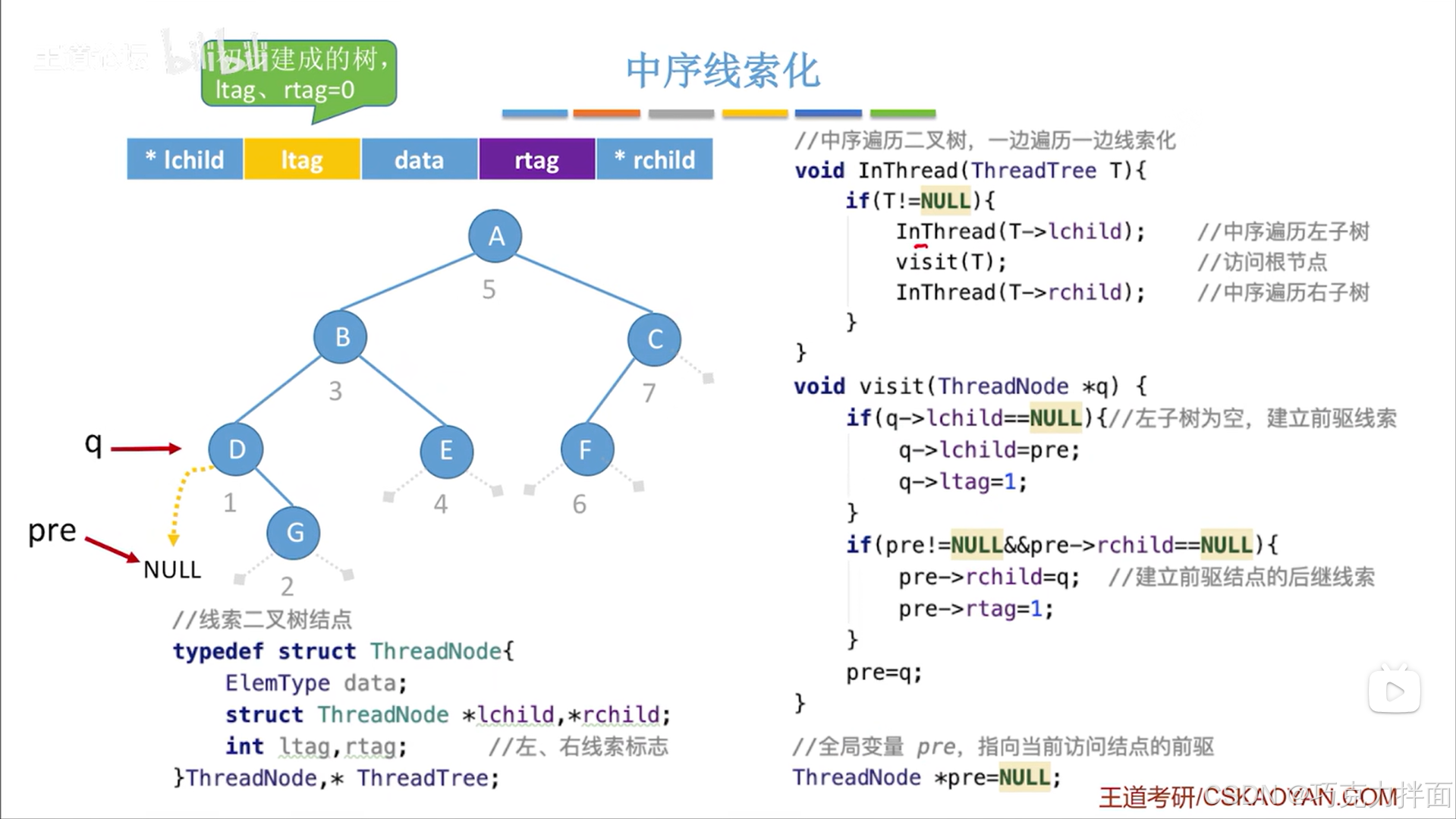
本例由于此时pre==NULL,所以不走第二个if语句,最后还需要把pre指针修改为指向当前结点,因为要开始访问下一个结点了(中序遍历二叉树即InThread函数可以实现访问下一个结点):
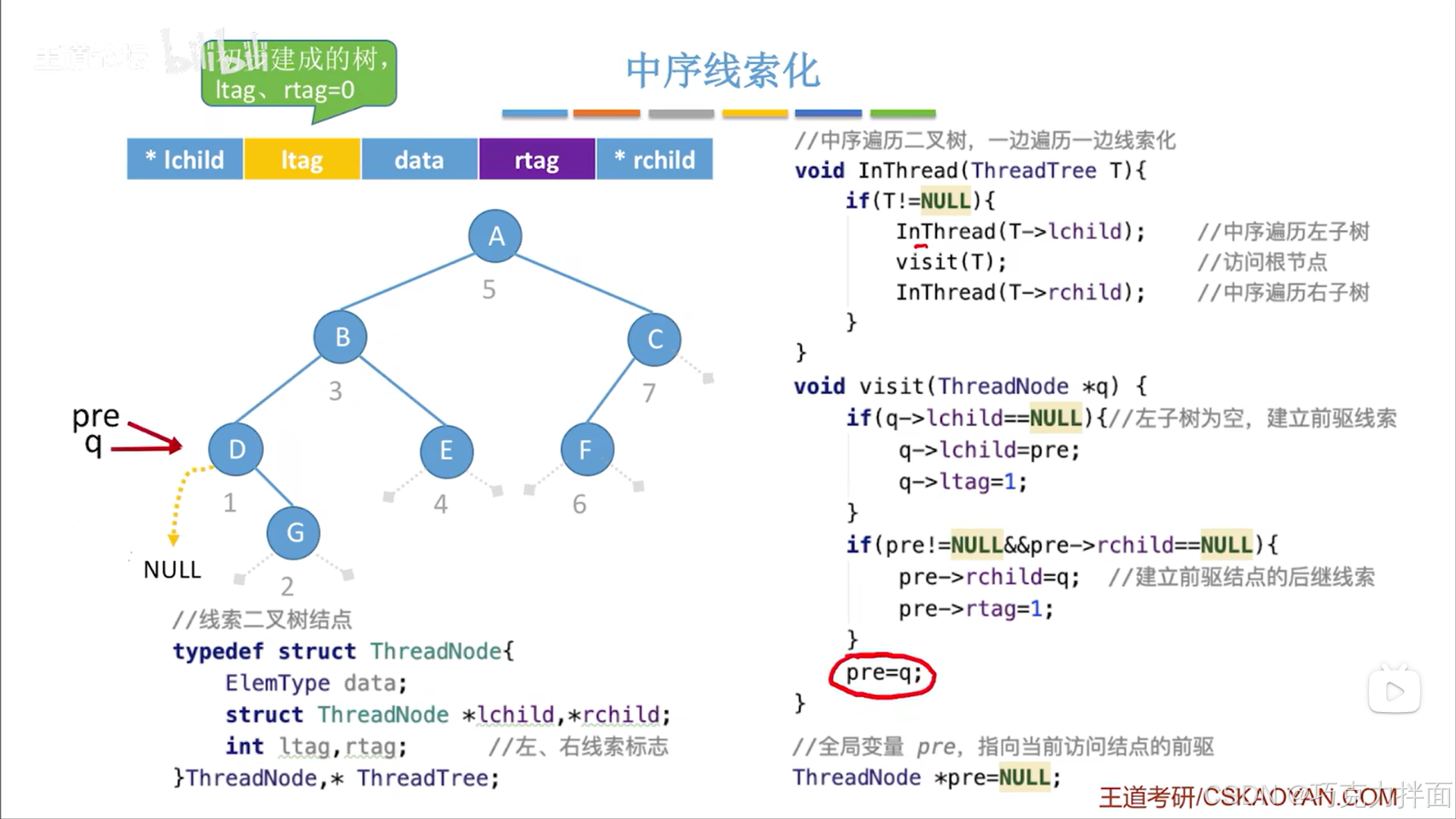
下一个被访问的结点为G结点:
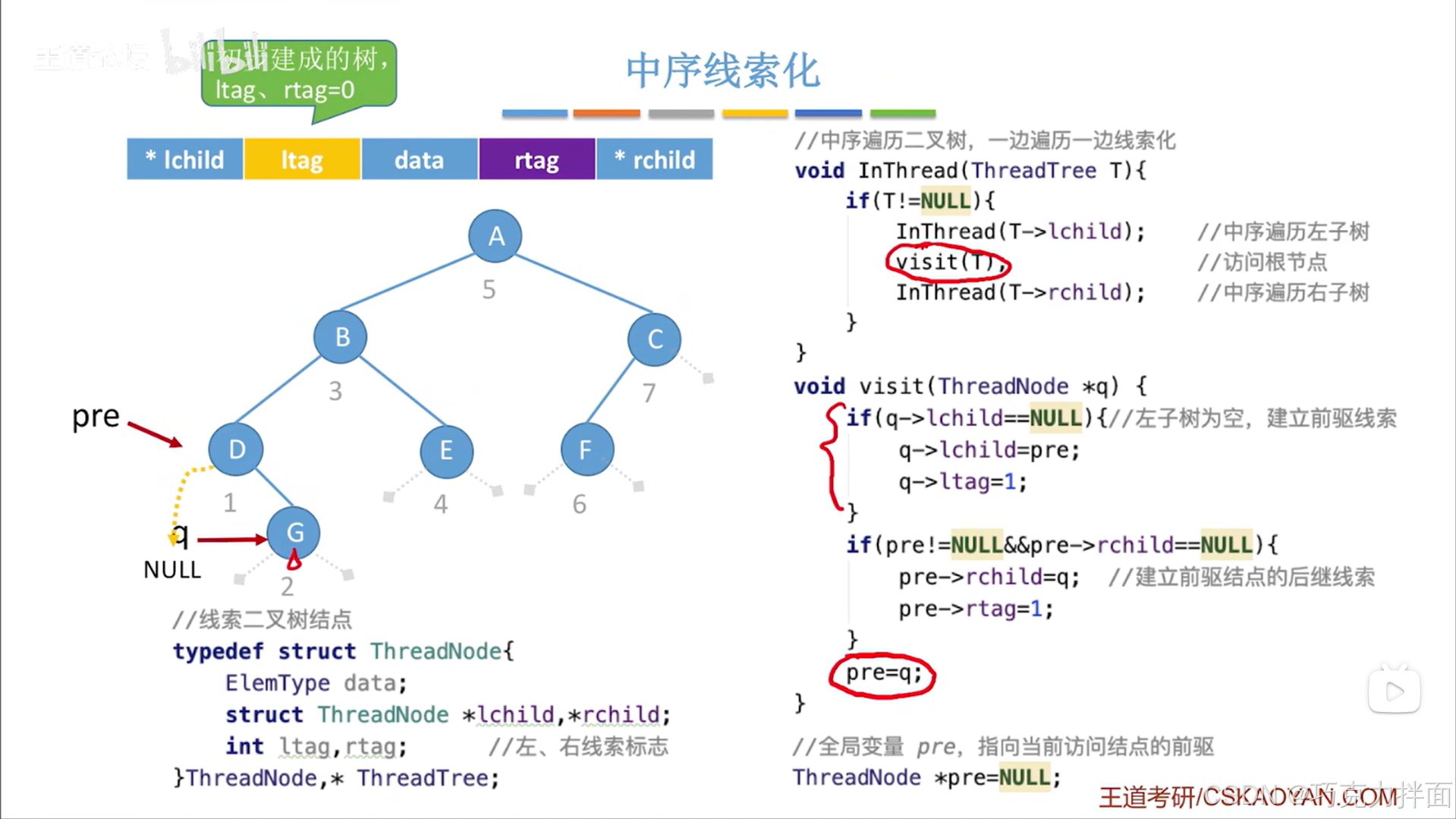
调用visit函数后,由于G结点的左孩子指针为空即q->lchild==NULL,所以要执行第一个if语句,要把左孩子指针线索化即把G结点的前驱赋值给G结点的左孩子指针,同时修改ltag的值,由于G结点的前驱结点即D结点的右孩子指针指向G结点即前驱的右孩子指针不为空,所以pre->rchild!=NULL,可知不执行第二个if语句:
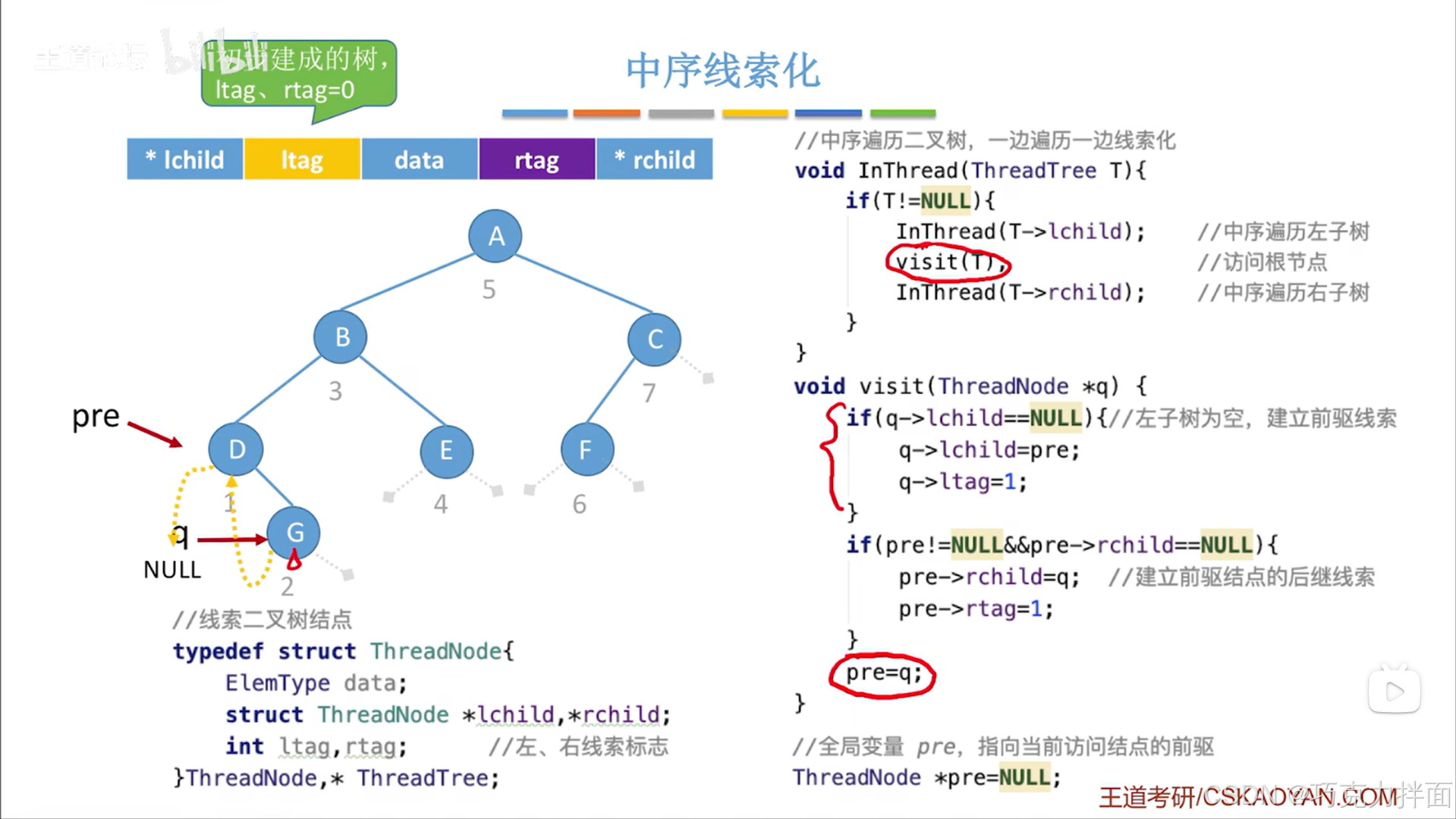
最后还需要把pre指针修改为指向当前结点,因为要开始访问下一个结点了(中序遍历二叉树即InThread函数可以实现访问下一个结点):
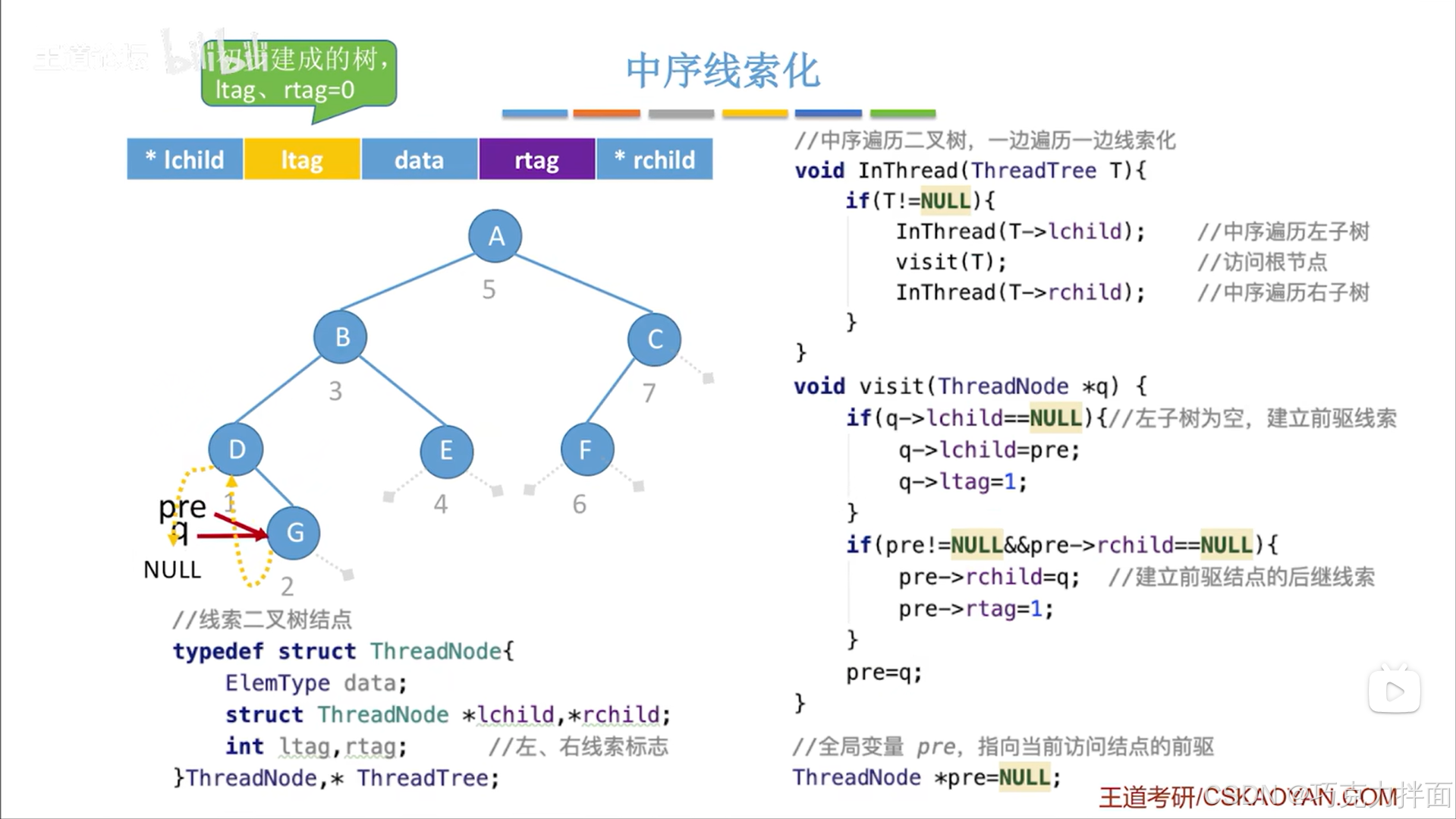
下一个被访问的结点为B结点:
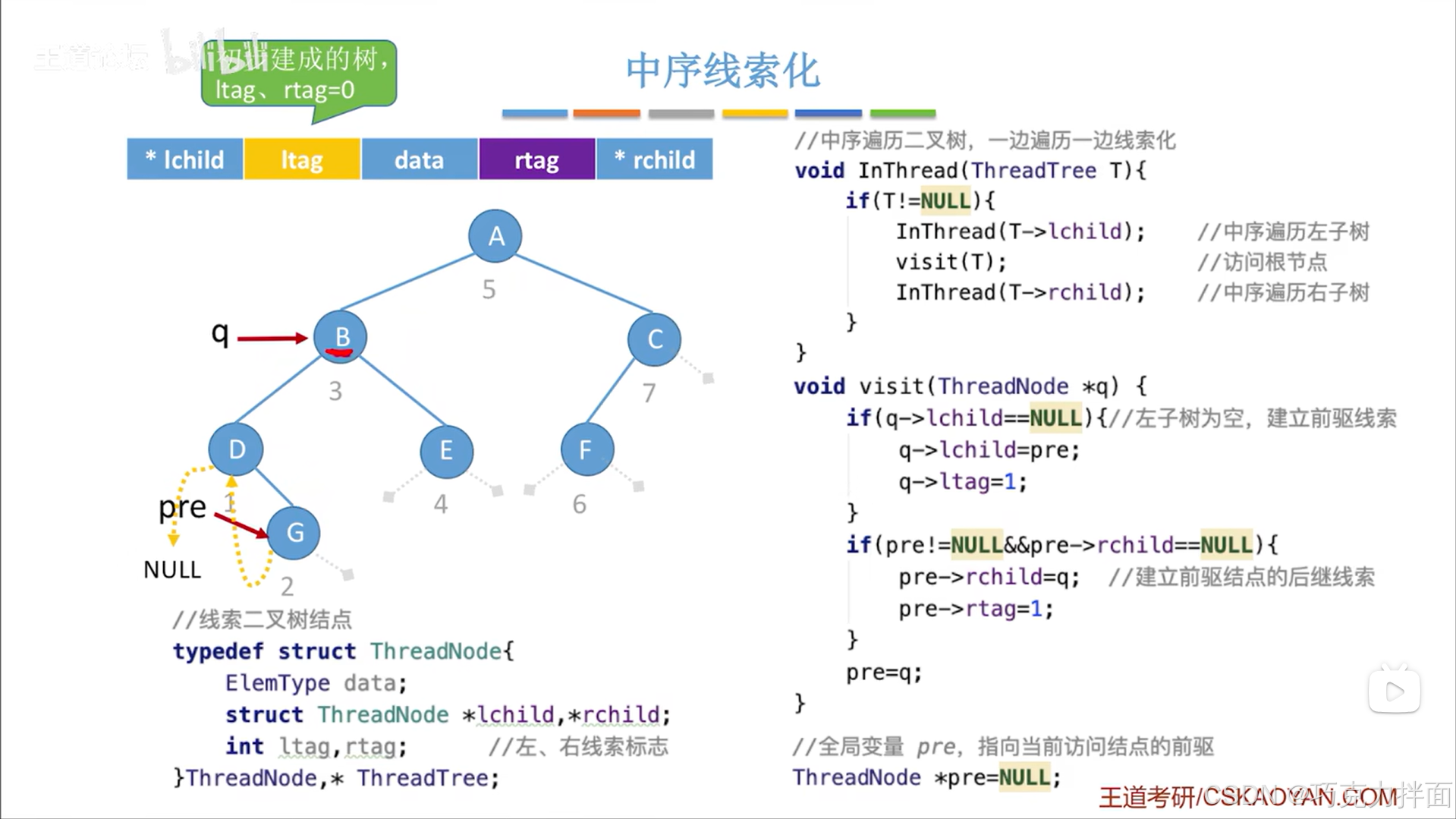
调用visit函数后,由于B结点的左孩子指针是非空的(B结点的右孩子指针也非空),所以第一个if语句不执行,但B结点的前驱结点G结点此时不为空且G结点的右孩子指针为空即pre!=NULL&&pre->rchild==NULL,所以要把B结点的前驱结点G结点的右孩子指针线索化,也就是G结点的右孩子指针指向G结点的后继结点B结点即pre->rchild=q,同时把rtag设为1表示被线索化:
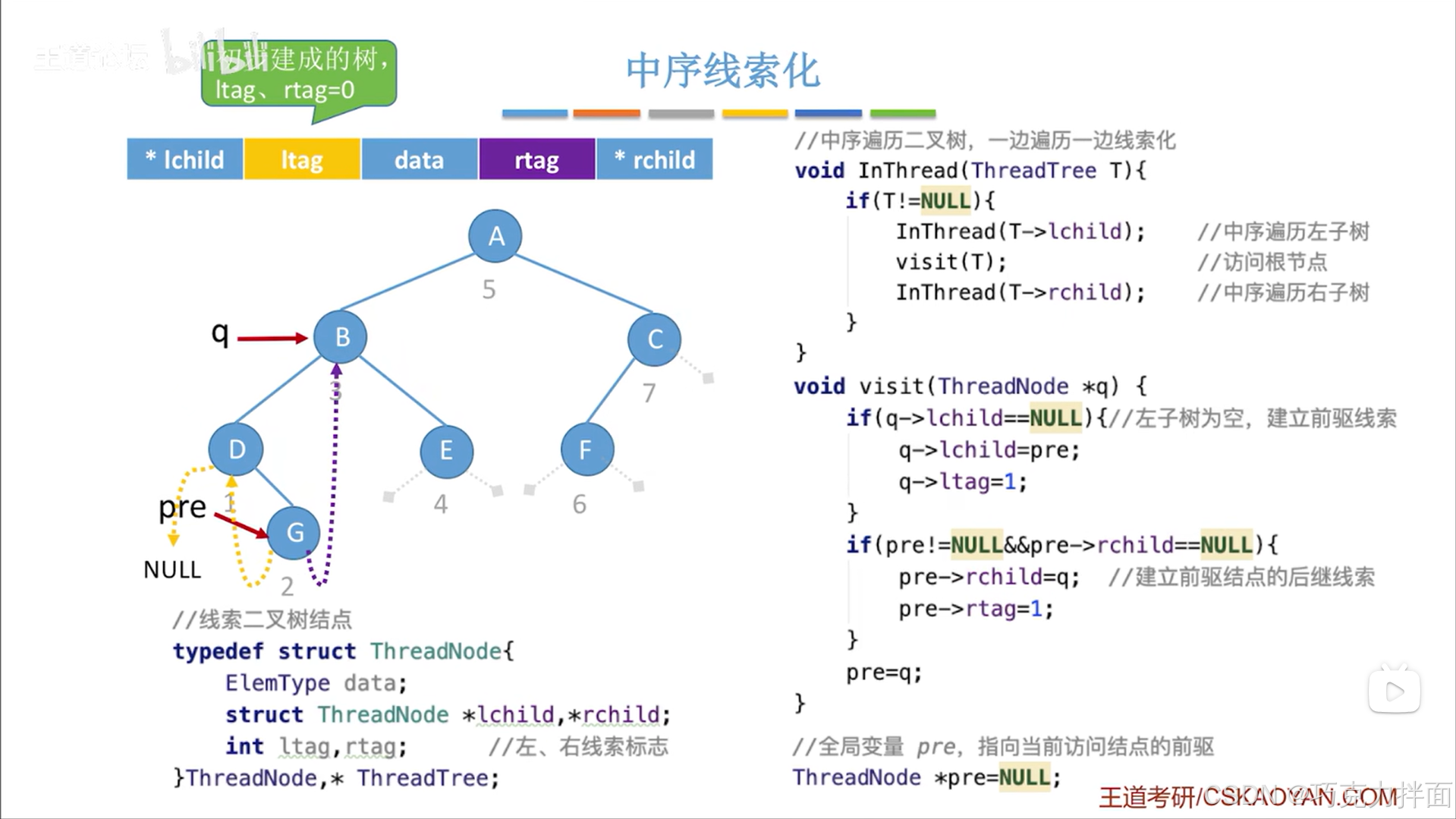
最后还需要把pre指针修改为指向当前结点,因为要开始访问下一个结点了(中序遍历二叉树即InThread函数可以实现访问下一个结点):
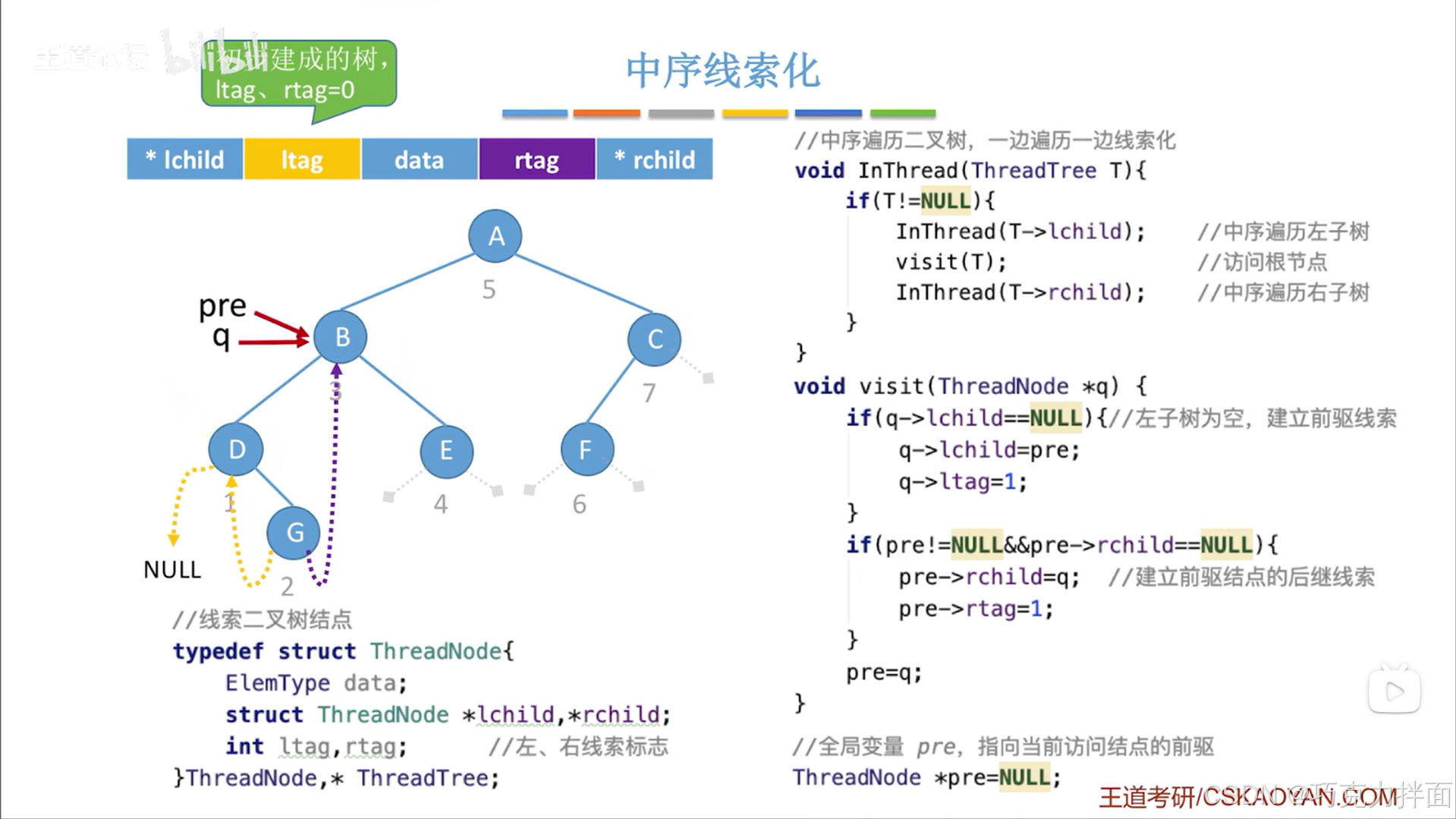
下一个被访问的结点为E结点:
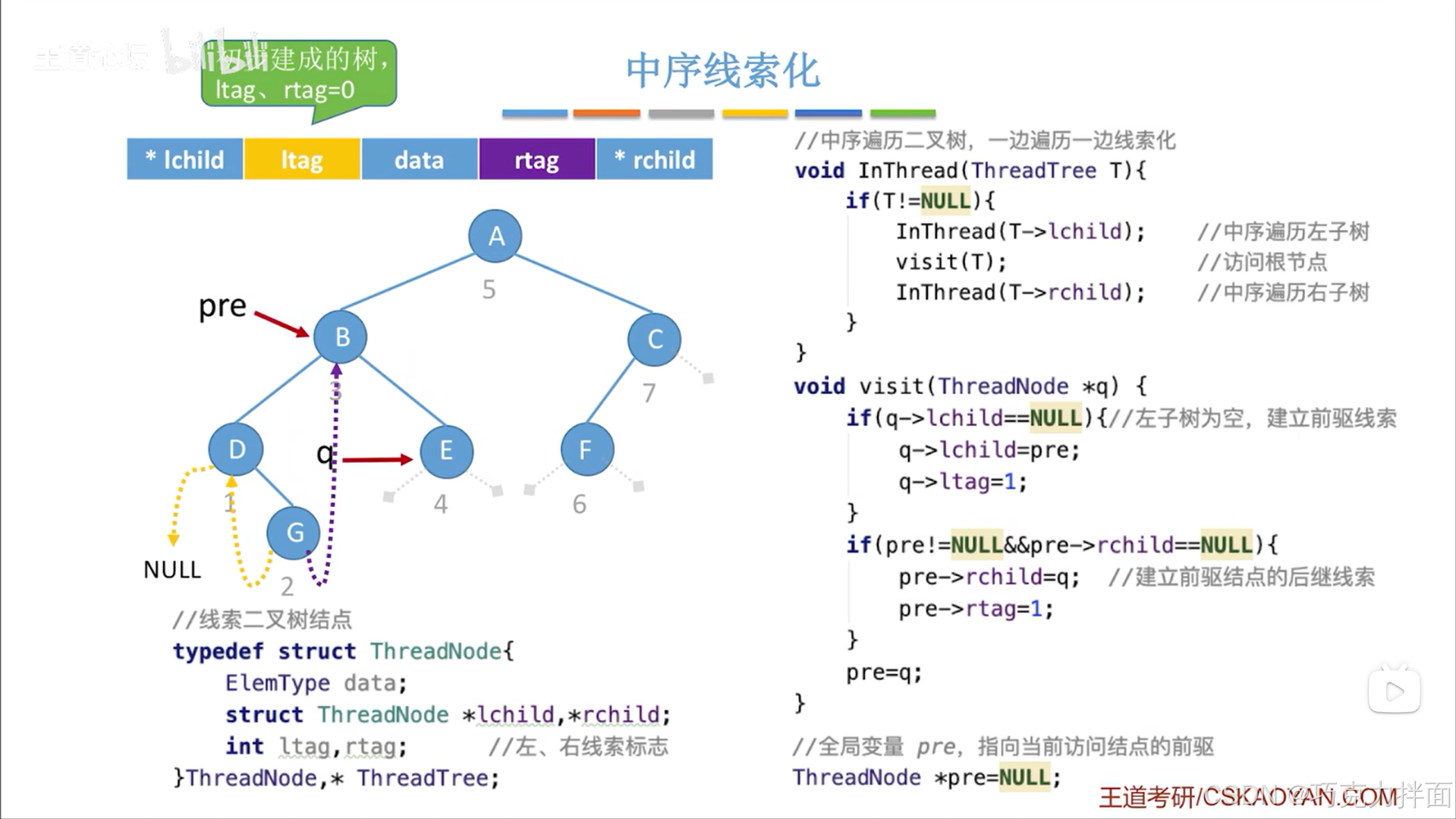
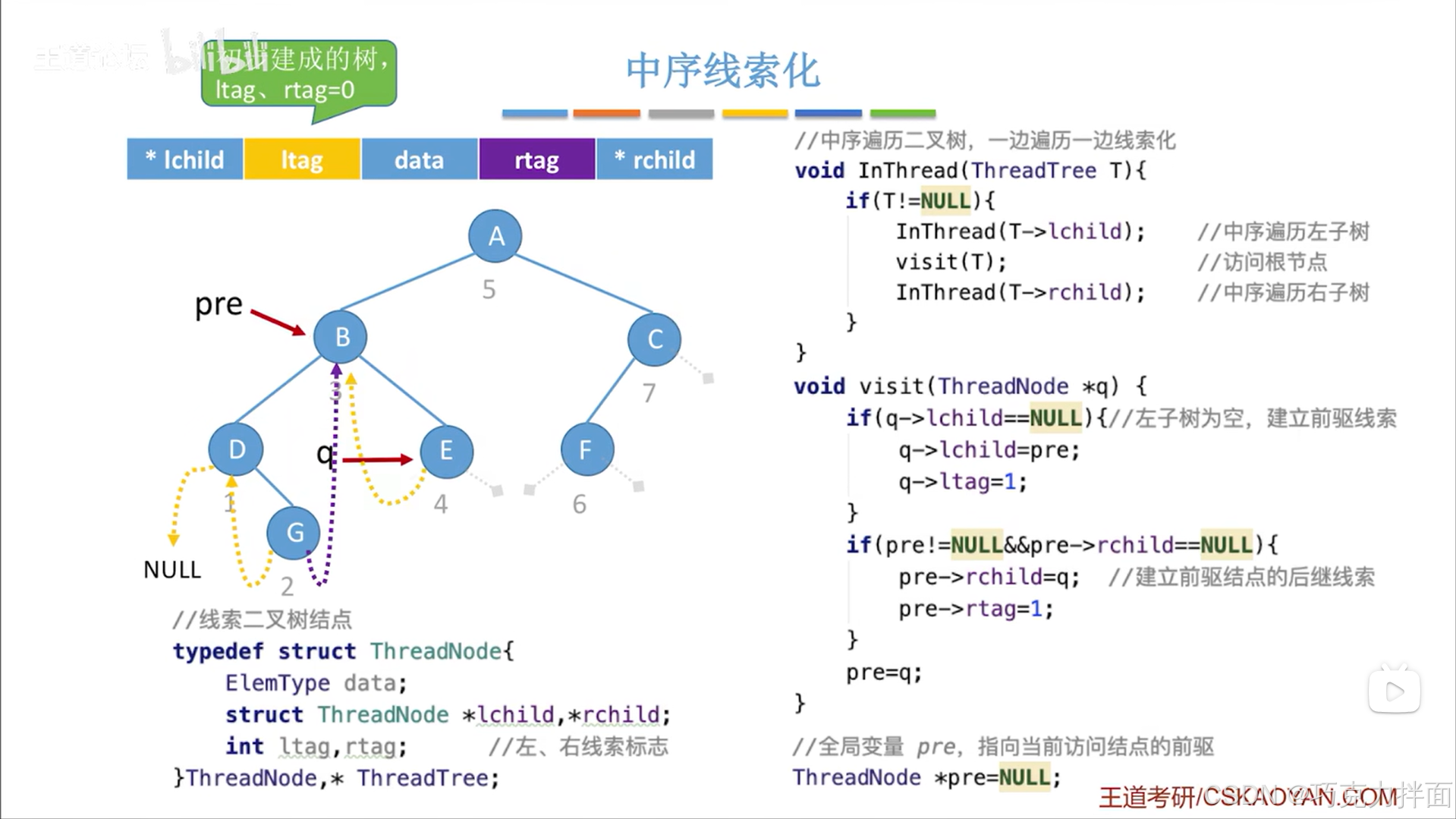
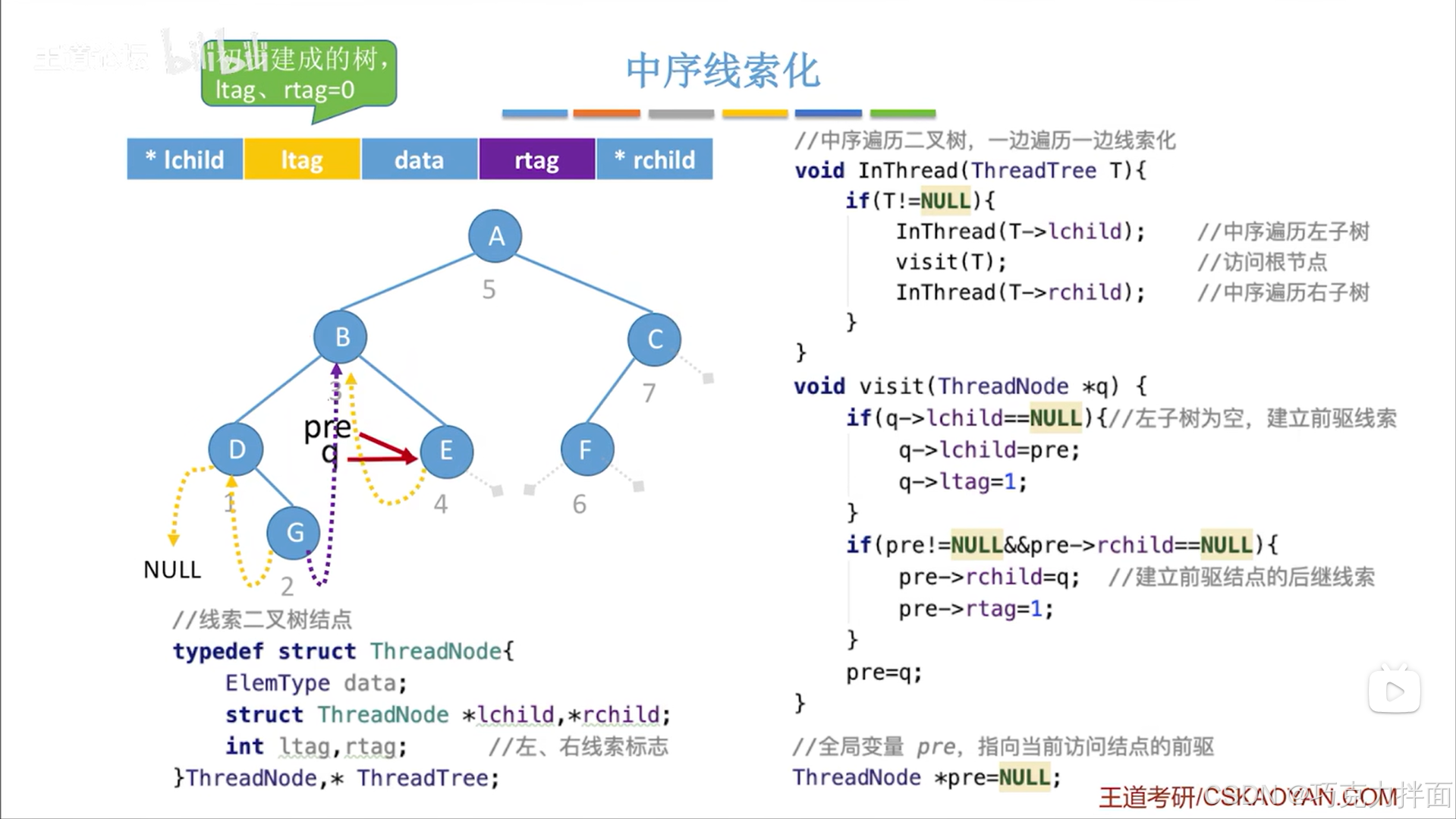
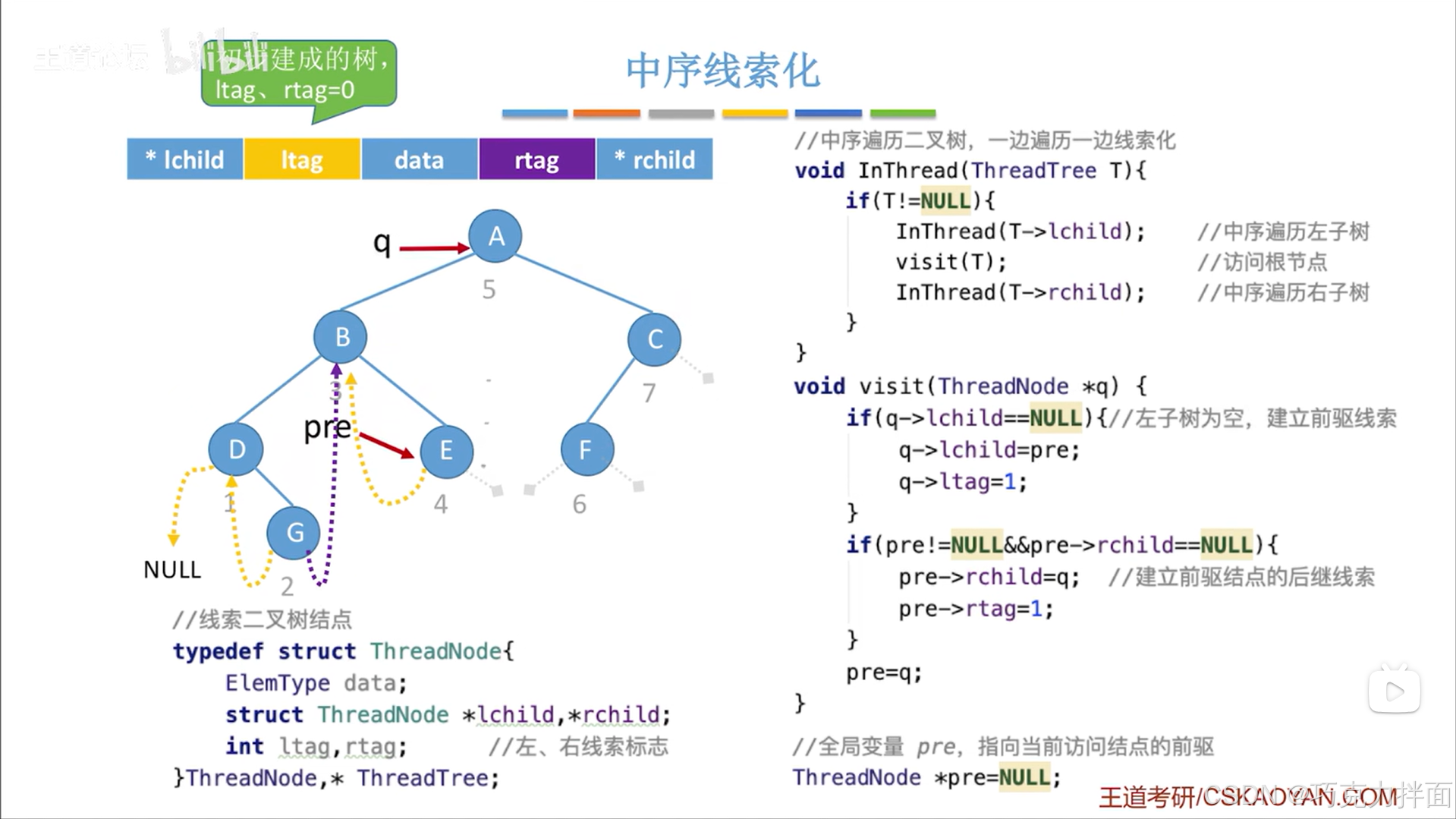
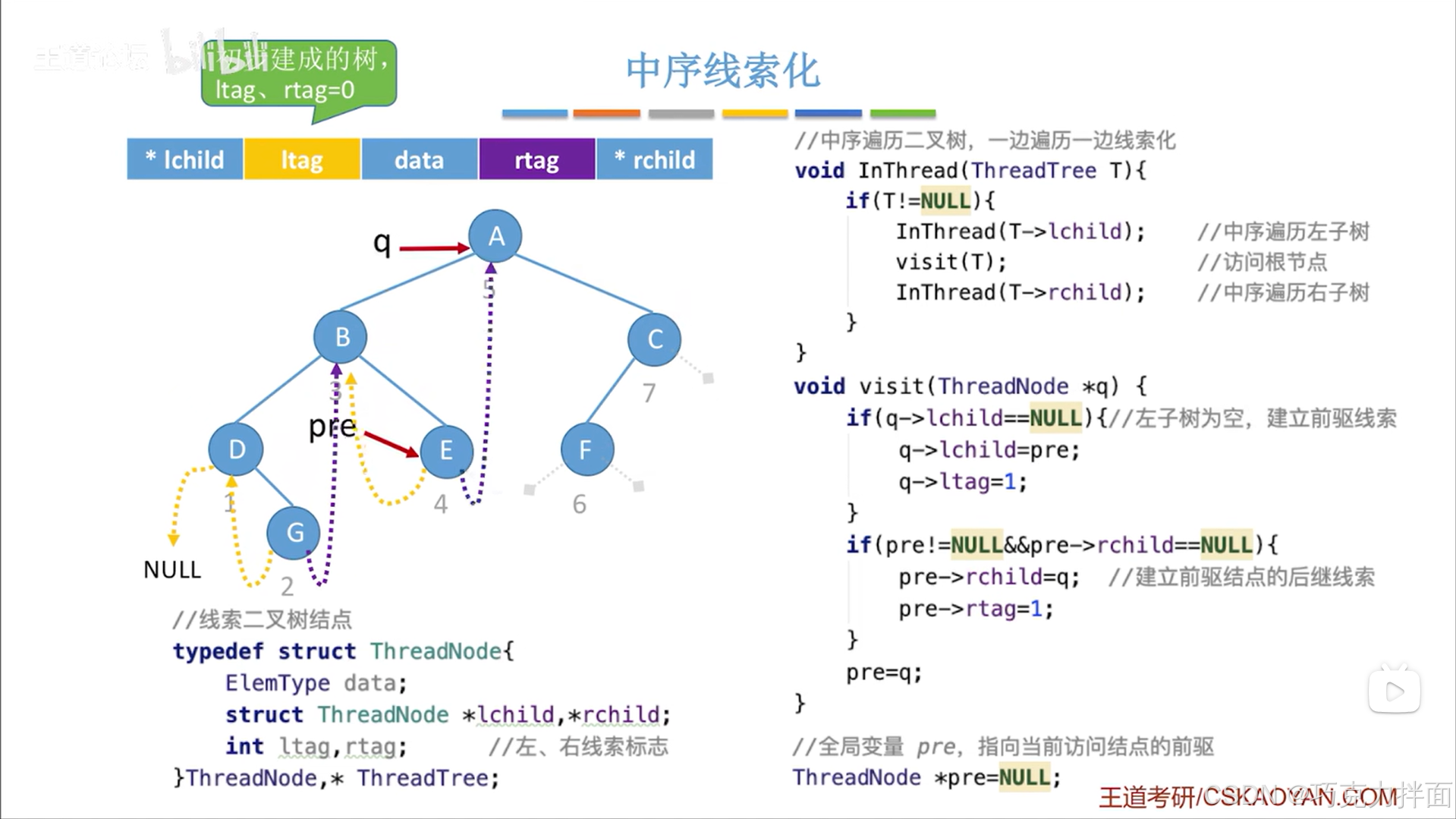
下一个被访问的结点为A结点:
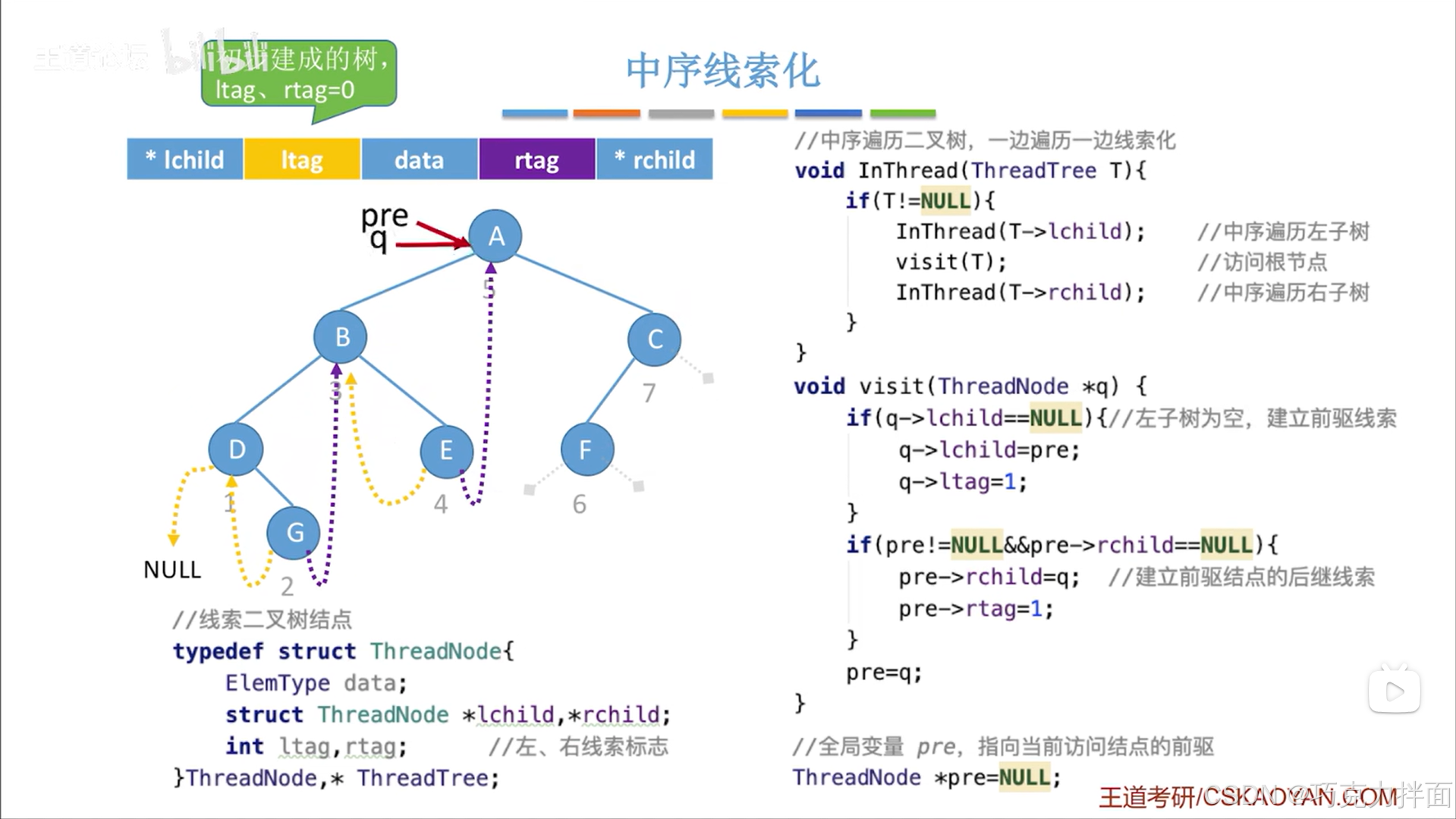
下一个被访问的结点为F结点:
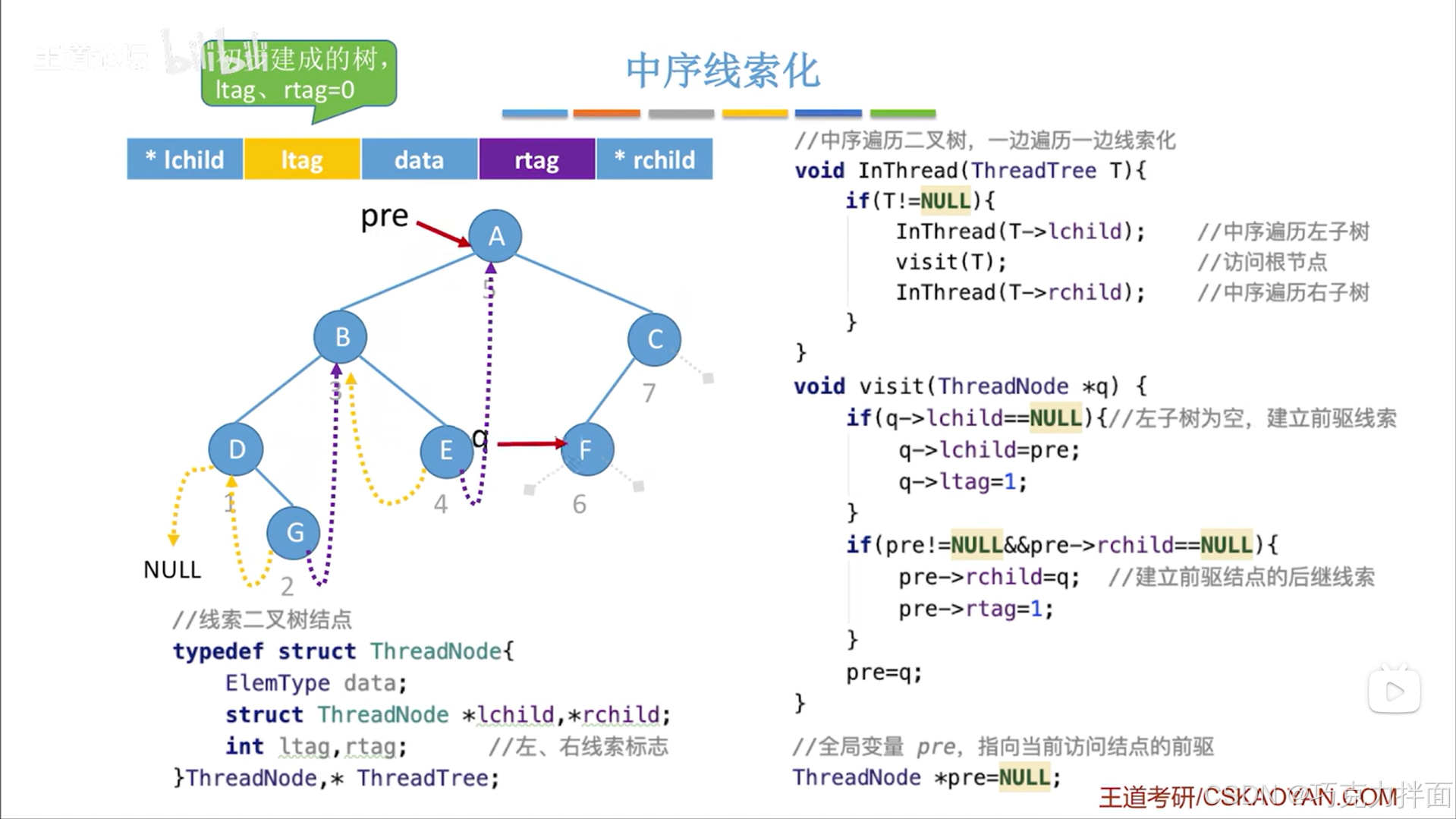
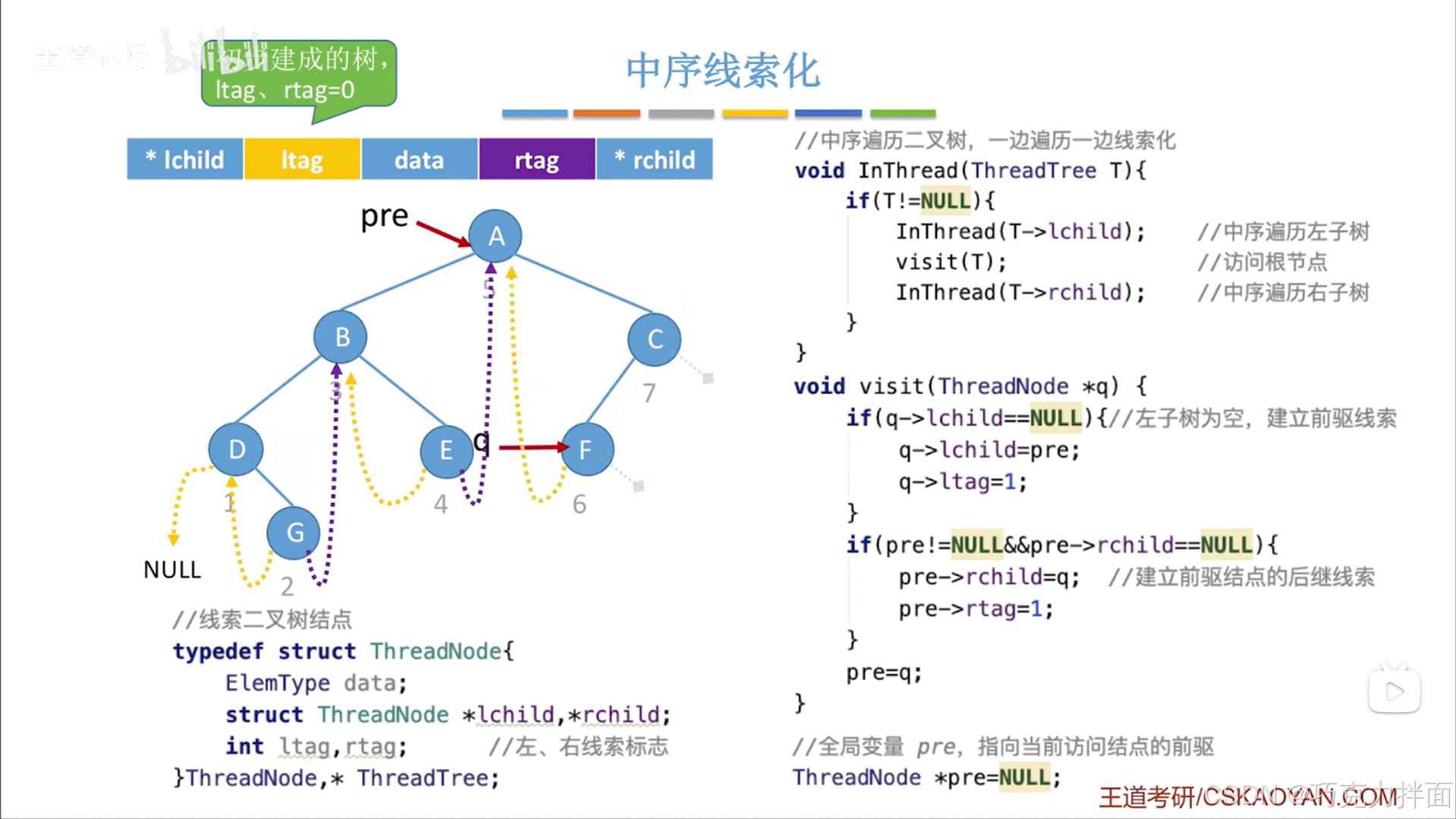
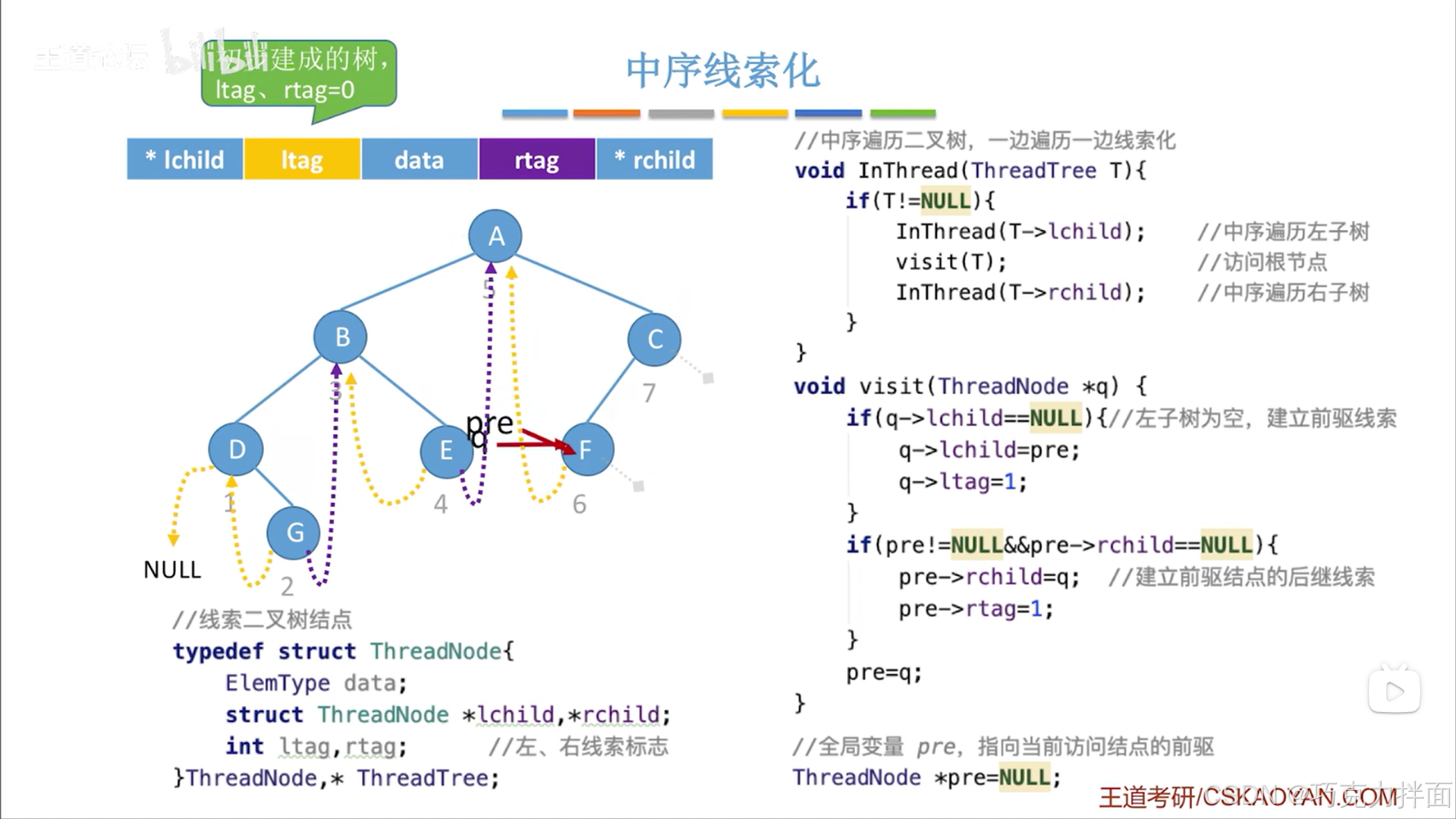
下一个被访问的结点为C结点:
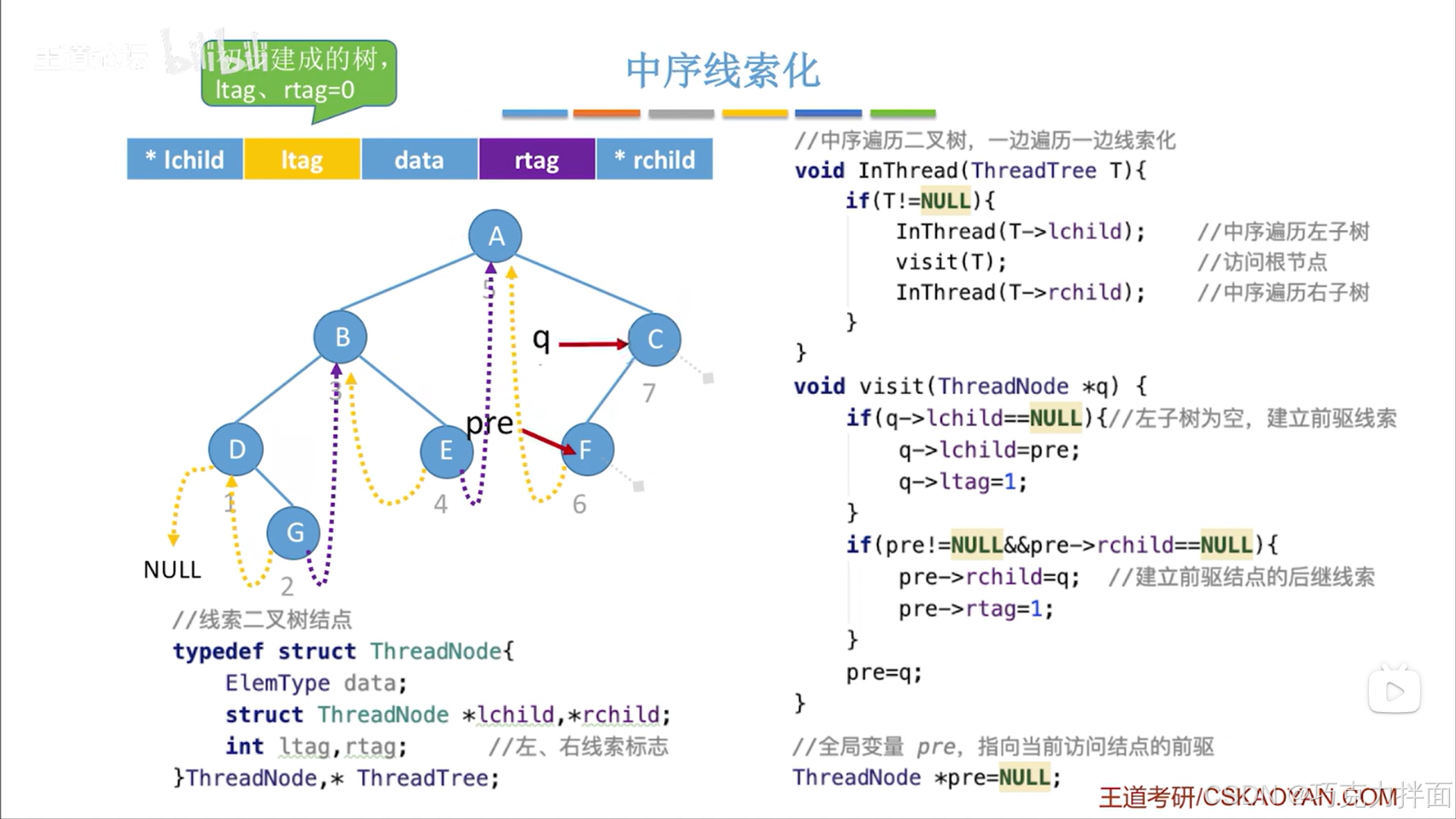
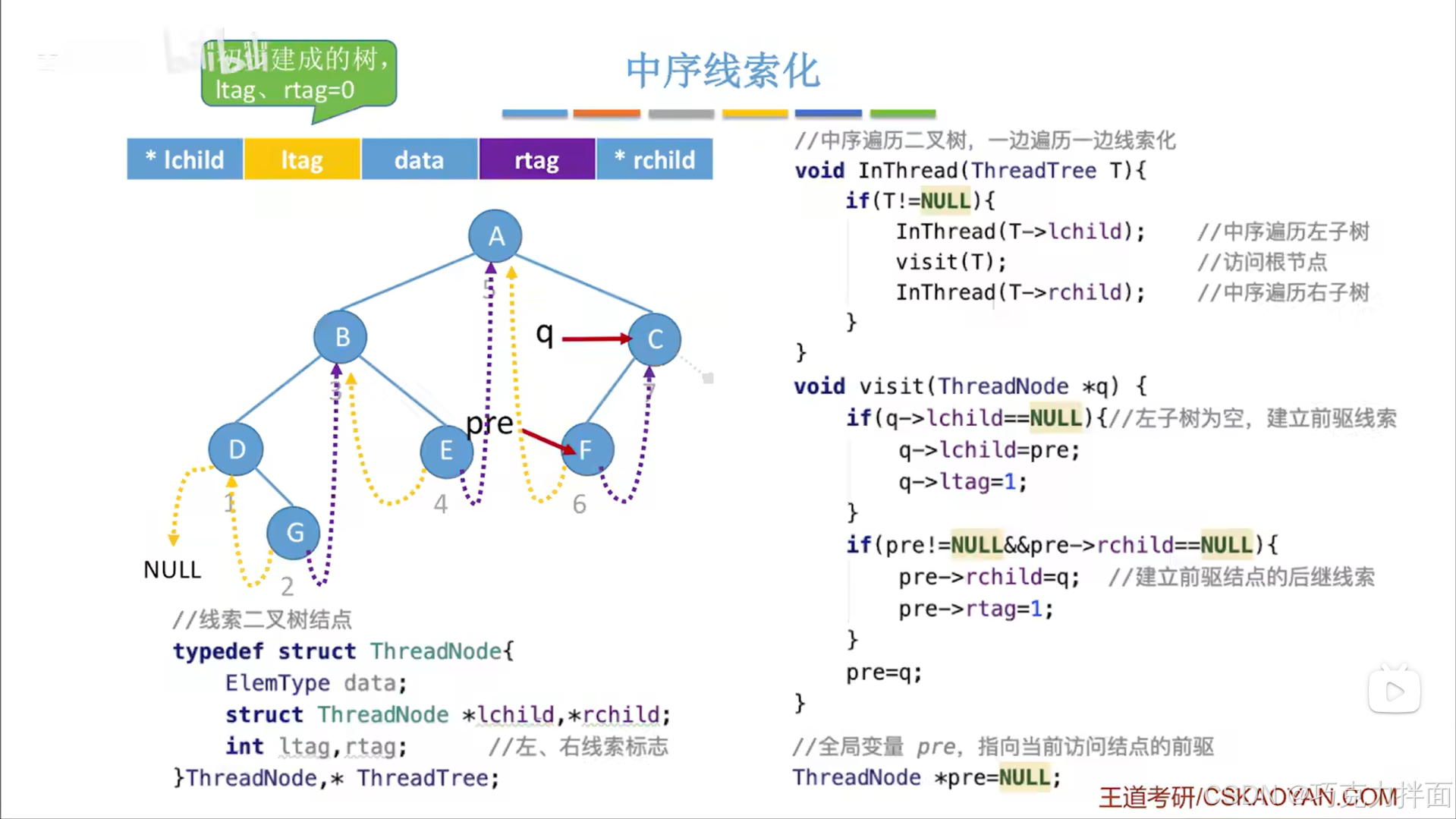
当访问到最后一个结点C结点时,调用visit函数,最后会把pre指针指向当前结点:
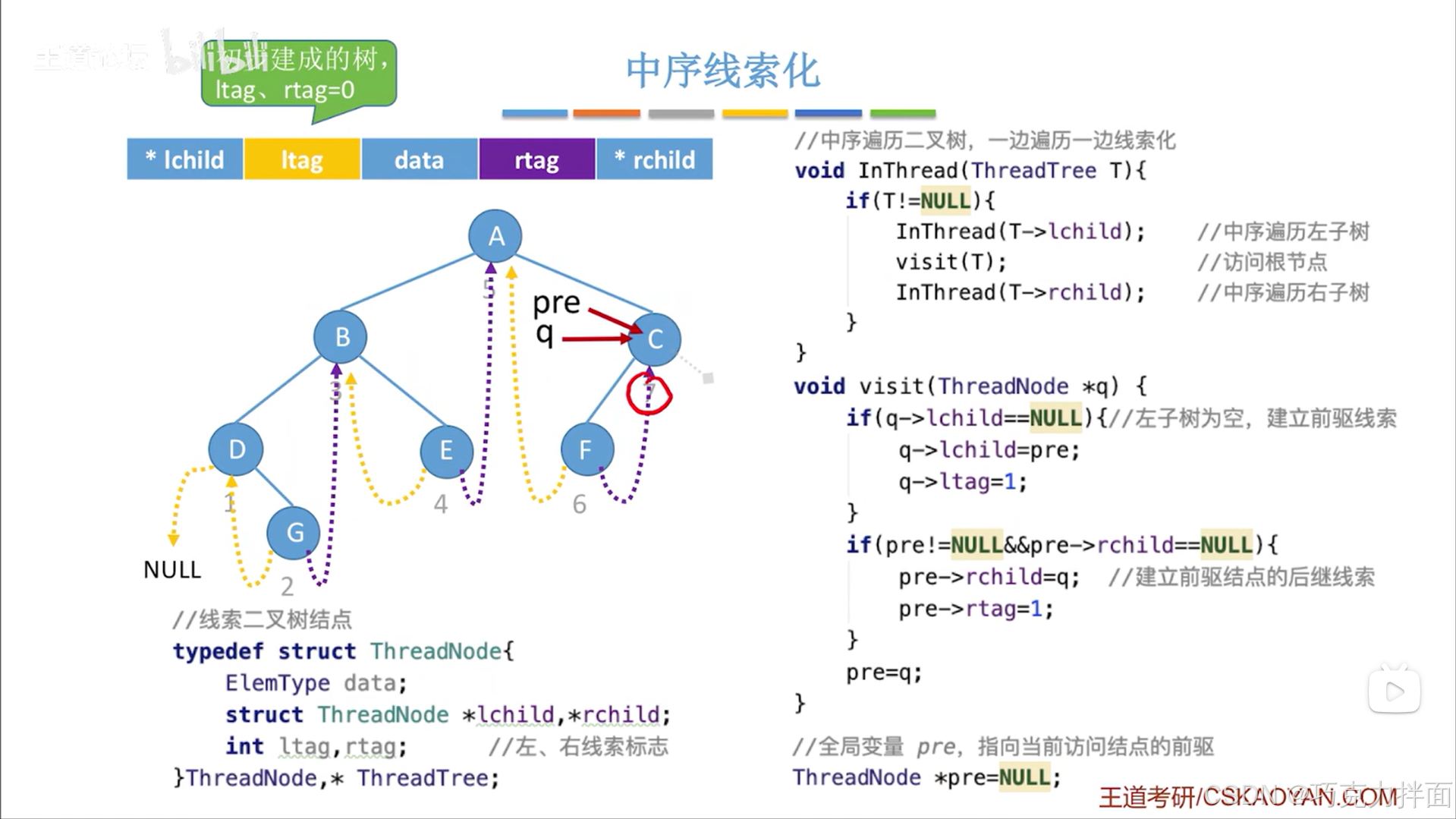
访问完最后一个结点即C结点后就不会再有结点被访问,但现在存在一个问题:当前结点的右孩子指针如果为空且要被线索化,这个线索化的过程是在访问下一个结点中实现,此时最后一个结点即C结点的右孩子指针是空的,应该把该结点的右孩子指针线索化,但由于C结点之后没有结点再被访问即无法通过visit函数实现C结点的右孩子指针线索化,不过还好这里设置的pre指针是一个全局变量,所以可以再设置一个函数,对pre指针当前指向的结点再进行一个处理,让最后一个结点C结点的右孩子指针指向NULL,也就是表示最后一个结点即C结点没有后继结点,同时把C结点的rtag设为1:核心就是看pre指针指向的结点的rchild即右孩子指针是否为空,如果为空,说明这是最后一个结点,最后一个结点没有后继结点,就把该结点的右孩子指针指向NULL,且rtag赋值为1->最后一个结点要特殊处理
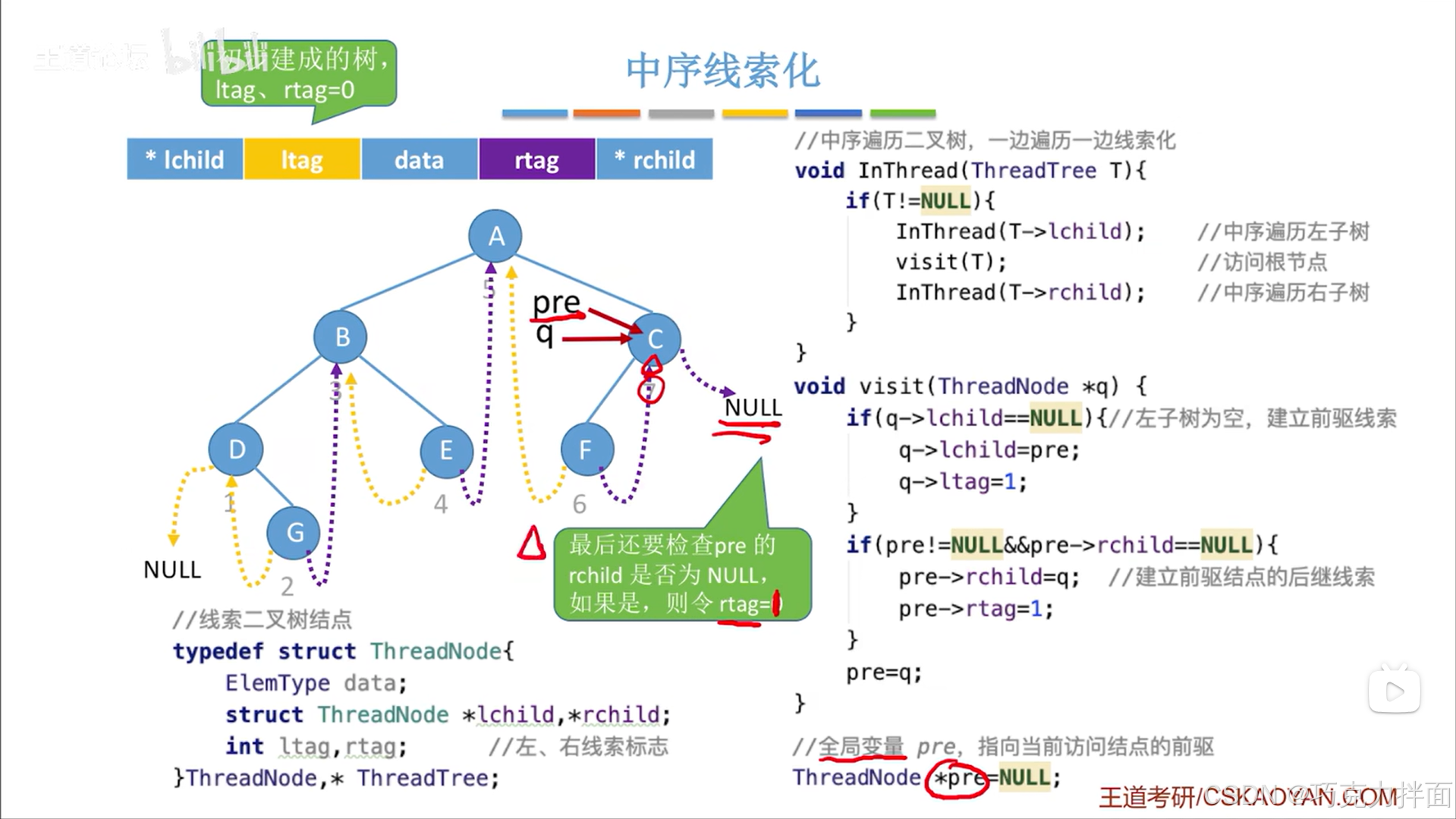
中序线索化的最终结果:
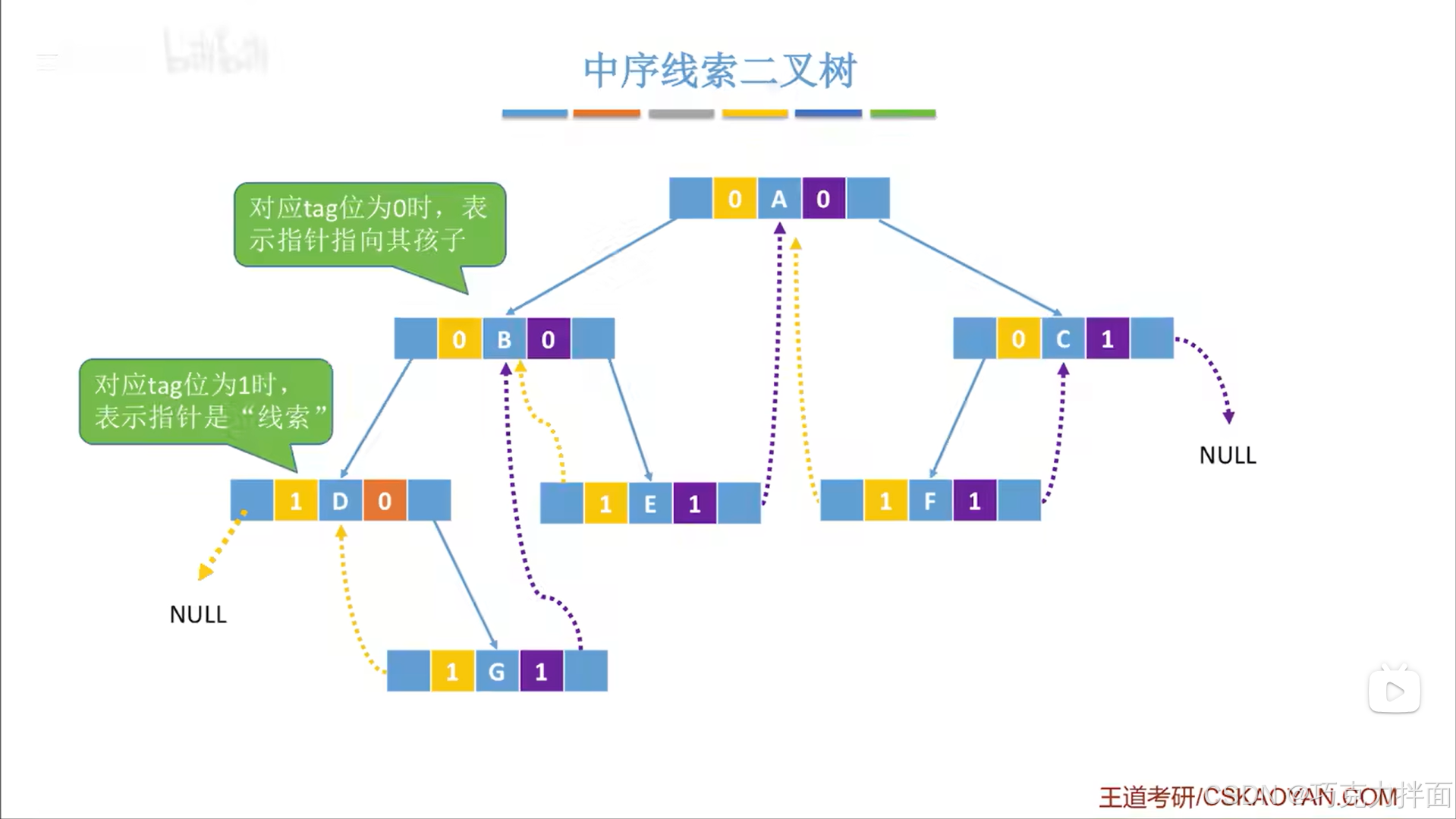
4.中序线索化完整代码:
方案一:

-
指针pre指向当前访问结点的前驱结点,一开始访问第一个结点,而第一个结点没有前驱结点,因此pre指向NULL即pre初始值为NULL
-
CreateInThread函数用于中序线索化二叉树,只有非空二叉树才能被线索化,线索化的核心在于InThread函数,InThread函数本质是在中序遍历二叉树,只不过是一边遍历一边把各个结点进行线索化
-
当处理到最后一个结点时,如果最后一个结点的右孩子指针是NULL的话就需要把该结点的rtag设为1
-
中序线索化本质就是在中序遍历二叉树,只不过是一边遍历一边把各个结点进行线索化
方案二:



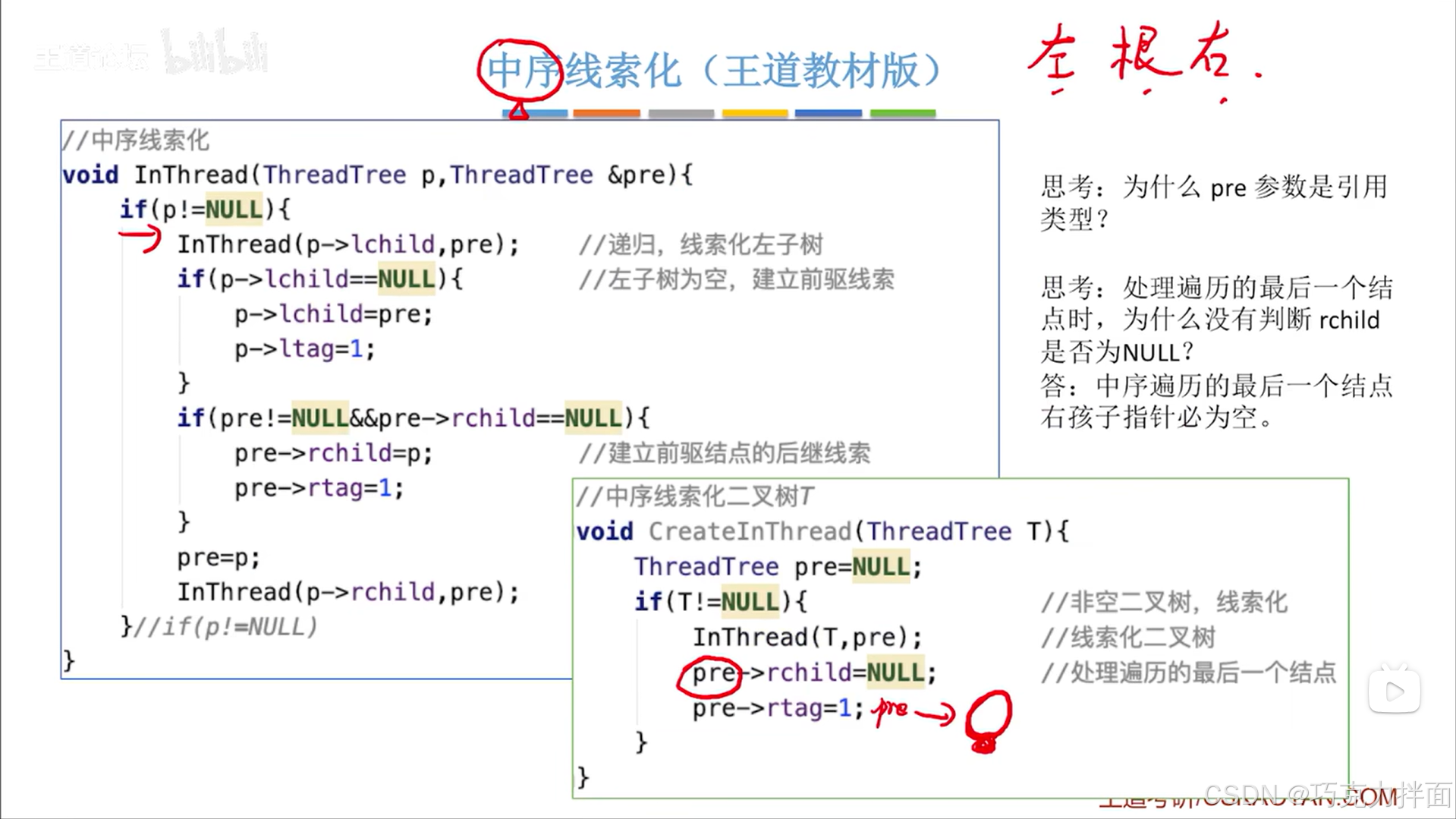
-
ThreadTree是二叉树的结点类型,p代表当前访问的结点,指针pre指向当前访问结点的前驱结点
-
InThread函数是用来中序线索化二叉树的,本质是中序遍历二叉树,只不过是一边遍历一边把各个结点进行线索化,当访问到的结点不为空时开始线索化
-
InThread函数中形参pre之所以是引用类型(用&修饰pre),这是为了保证在CreateInThread函数里调用InThread函数后,InThread函数中对pre进行修改可以影响到CreateInThread函数里的pre的值即影响到原始的pre的值,但如果不用&修饰pre,在CreateInThread函数里调用InThread函数后,InThread函数里的pre的值都只是CreateInThread函数里的pre的复制品而已->总而言之,在CreateInThread函数里调用InThread函数后,InThread函数中形参pre用&修饰后就把pre的作用范围从CreateInThread函数扩展到InThread函数中了
-
CreateInThread函数里处理遍历的最后一个结点时,并没有判断rchild是否为NULL,而是直接把最后一个结点的右孩子指针指向NULL,rtag赋值为1,这里为什么这么做呢?万一最后一个被访问的结点,它的右孩子指针不为空也就是最后一个结点的右孩子指针指向一个结点呢,此时如果直接把最后一个结点的右孩子指针指向NULL,岂不是把最后一个结点的右孩子指针指向的结点丢失了,其实原因就是在中序线索化中进行中序遍历的时候,访问二叉树的顺序是左、根、右,此时假设最后一个被访问的结点还有一个右孩子的话即最后一个被访问的结点的右孩子指针指向一个结点,那么按照中序遍历的规则的话,左、根、右,就意味着访问完最后一个结点时还需要访问该结点右孩子指针指向的结点,意味着访问完最后一个结点后还需要访问结点,这与最后一个结点的定义矛盾,所以可以断定在中序遍历中最后一个被访问的结点是没有右孩子的即右孩子指针并没有指向结点(最后一个结点的左孩子指针要么指向结点,要么被线索化,所以最后一个结点的左孩子指针是不需要特殊处理的)
#include<stdio.h>
//线索二叉树的结点
typedef struct ThreadNode
{
int data; //结点数据内容
struct ThreadNode *lchild,*rchild; //左、右孩子指针
int ltag,rtag; //左、右线索标志
}ThreadNode,* ThreadTree;
//全局变量pre,指向当前访问结点的前驱
ThreadNode *pre=NULL;
//中序线索化
void InThread(ThreadTree p,ThreadTree &pre) //形参多了个pre是因为结点线索化需要前驱结点
{
if(p!=NULL) //p代表二叉树里的结点
{
InThread(p->lchild,pre); //递归,线索化左子树
/*从这里开始线索化结点*/
if(p->lchild == NULL) //左子树为空,建立前驱线索
{
p->lchild = pre;
p->ltag = 1;
}
if(pre!=NULL && pre->rchild == NULL)
{
pre->rchild = p; //建立前驱结点的后继线索
pre->rtag = 1;
}
pre = p; //标记当前结点成为刚刚访问过的结点
/*到这里该结点线索化结束*/
InThread(p->rchild,pre); //递归,线索化右子树
}
}
//中序线索化二叉树T
void CreateInThread(ThreadTree T)
{
ThreadTree pre=NULL;
/*此时既有全局变量的pre,也有局部变量的pre,会优先使用局部变量pre*/
if(T!=NULL) //非空二叉树,线索化
{
InThread(T,pre); //线索化二叉树
pre->rchild = NULL; //处理遍历的最后一个结点
pre->rtag = 1;
}
}
int main()
{
return 0;
}
5.先序线索化完整代码:
q结点代表当前访问到的结点。
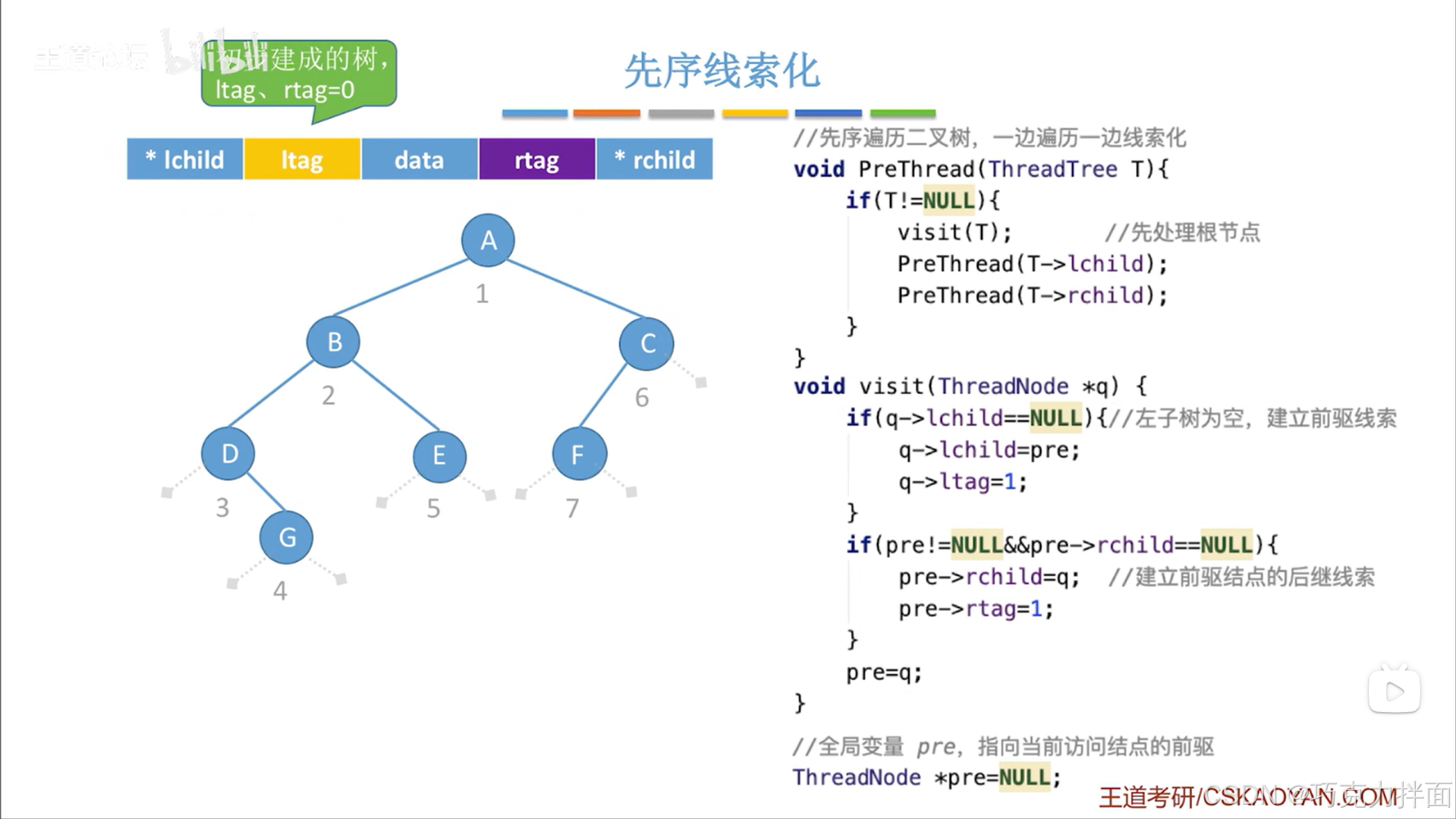
根据先序遍历规则可知上述二叉树的结点访问顺序为ABDGECF,假设此时访问到第三个结点D结点时,那么前驱指针pre就应该指向第二个被访问的结点B结点,按照visit函数的处理逻辑应该把第三个被访问的结点D结点的左孩子指针线索化,也就是D结点的左孩子指针指向D结点的前驱结点B结点,同时要把pre指针指向当前访问的结点:
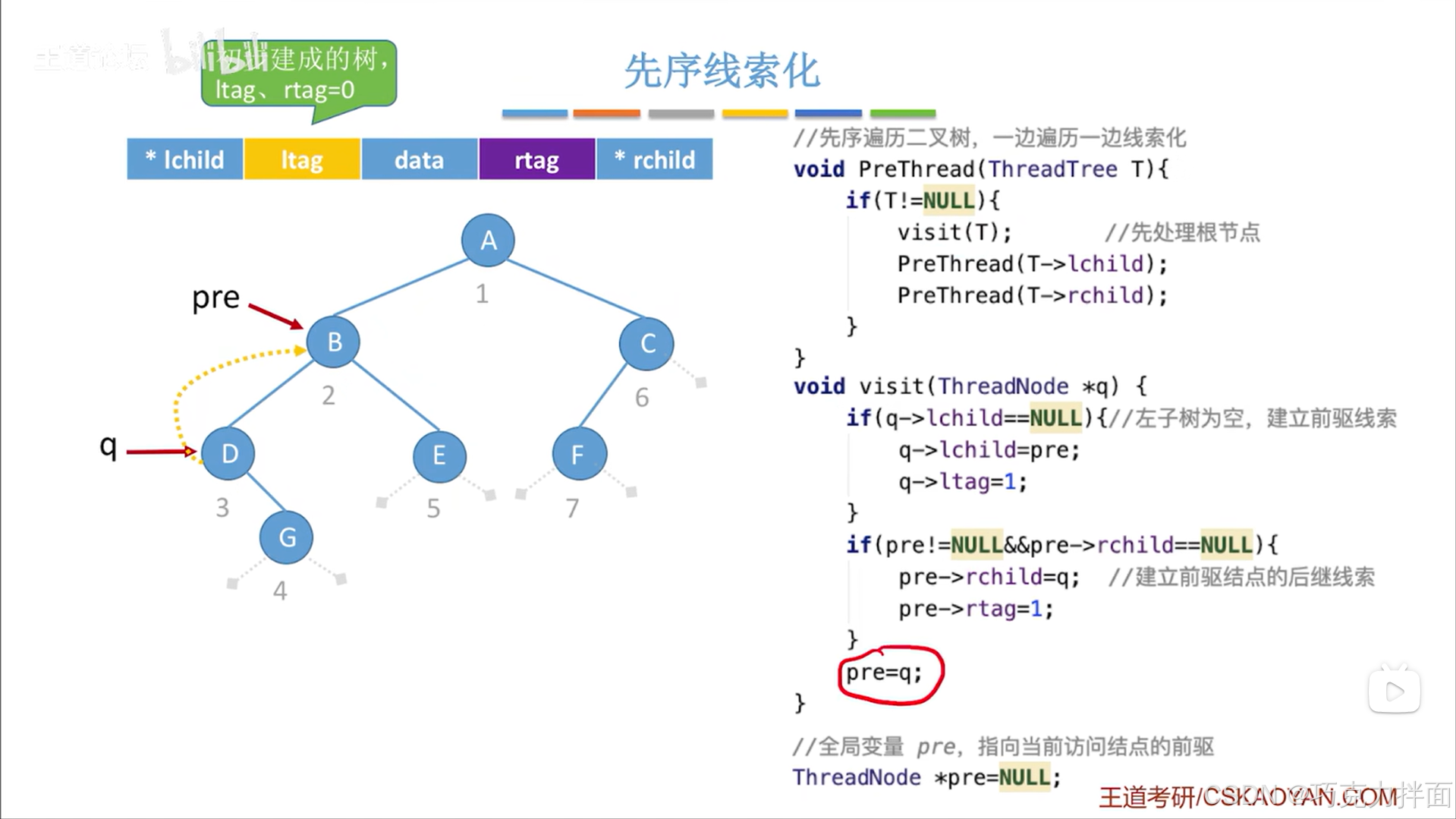
由于是先序遍历,所以当访问完第三个结点D结点时,还会处理D结点的左子树,但是在这之前已经把D结点的左孩子指针指向了它的前驱结点B结点了,所以接下来访问D结点的左子树的话,就会导致q结点再次访问B结点,也就是会出现对B结点和D结点的无限循环访问,这就是先序线索化中的"爱滴魔力转圈圈"问题,为了解决这个问题,可以利用左、右线索标志,当D结点的左孩子指针被线索化之后,ltag从0被赋值为1,此时可以通过ltag变量来判断D结点的左孩子指针指向的到底是否是真正的左孩子(当左孩子指针被线索化后就说明左孩子指针此时指向的并不是真正的左孩子,此时ltag为1,当ltag为0时说明左孩子指针此时指向的是真正的左孩子),所以要把访问结点左子树的代码进行修改:访问结点右子树的代码无需修改,因为造成上述循环访问结点的原因是在线索化一个结点的左孩子指针后就立即再次访问该结点左孩子指针上的结点,而线索化一个结点的右孩子指针后就会访问下一个结点,不会循环访问
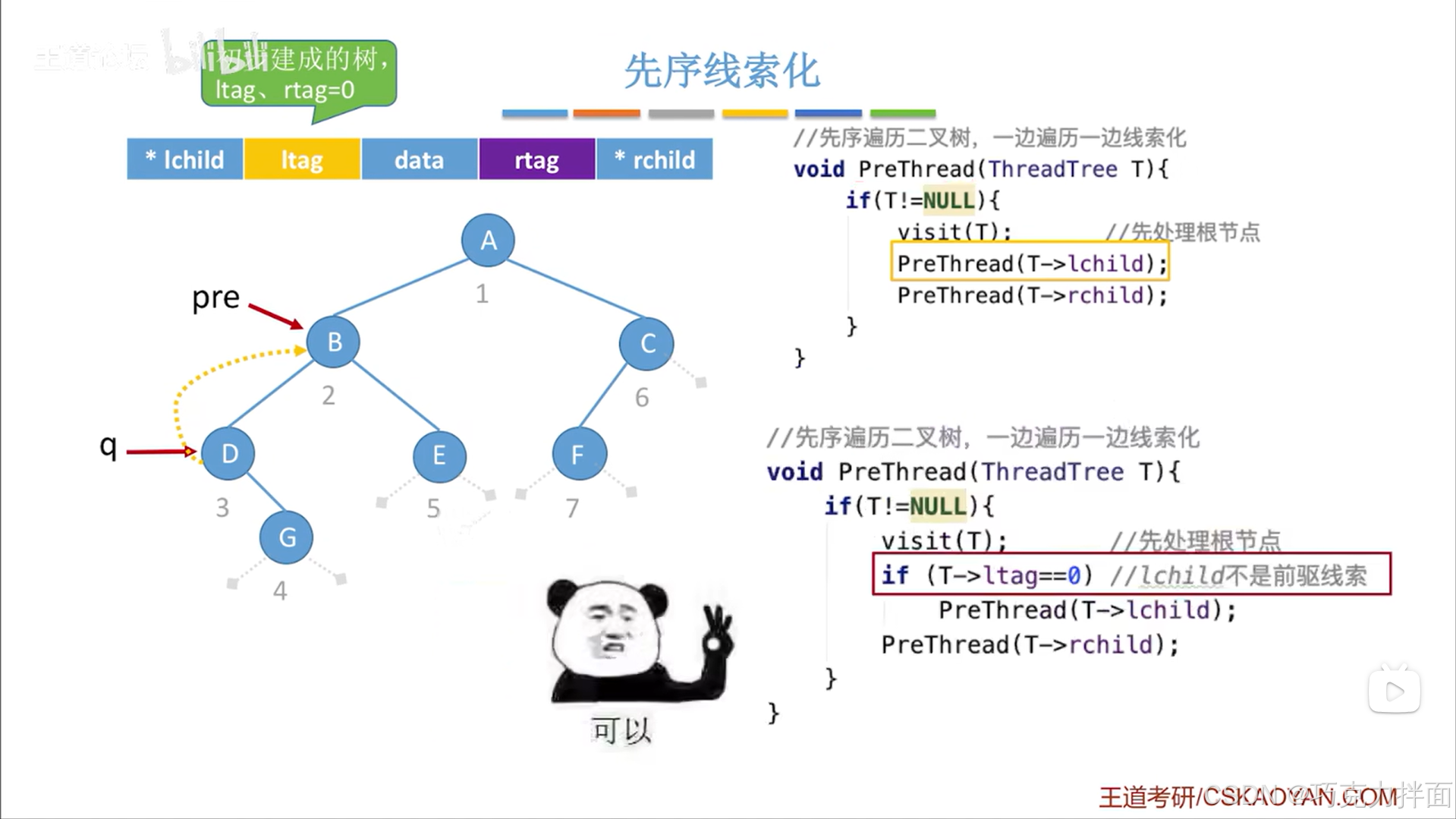
方案一:
最终完整代码:和中序线索化类似,最终需要特殊处理最后一个被访问的结点

方案二:
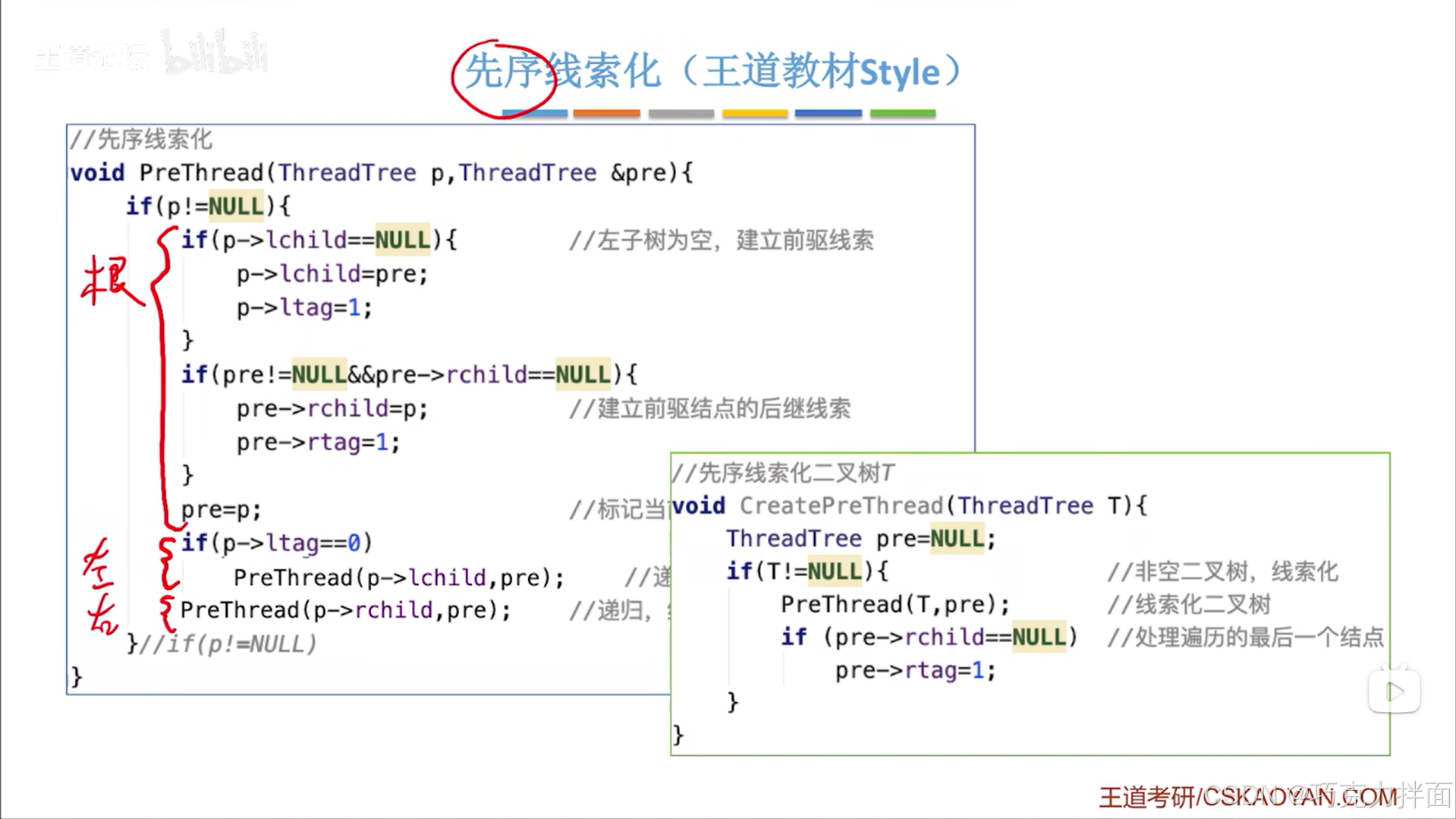
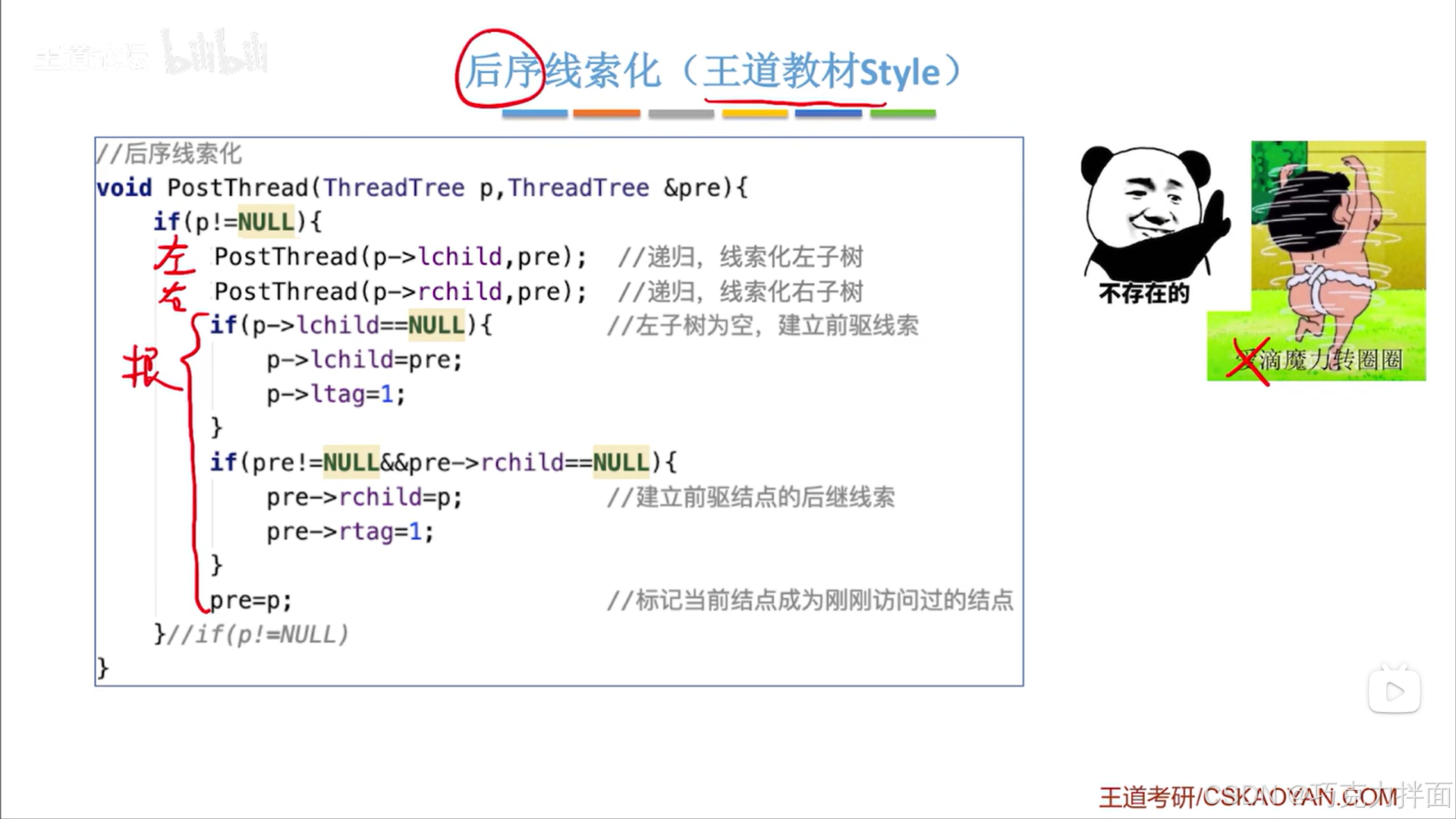
6.后续线索化完整代码:
后续线索化不会出现先序线索化中循环访问结点的问题,因为当访问一个结点时,这个结点的左孩子指针和右孩子指针都已经处理完毕,所以访问完该结点时不可能再回头去访问该结点的左孩子指针和右孩子指针所指向的内容
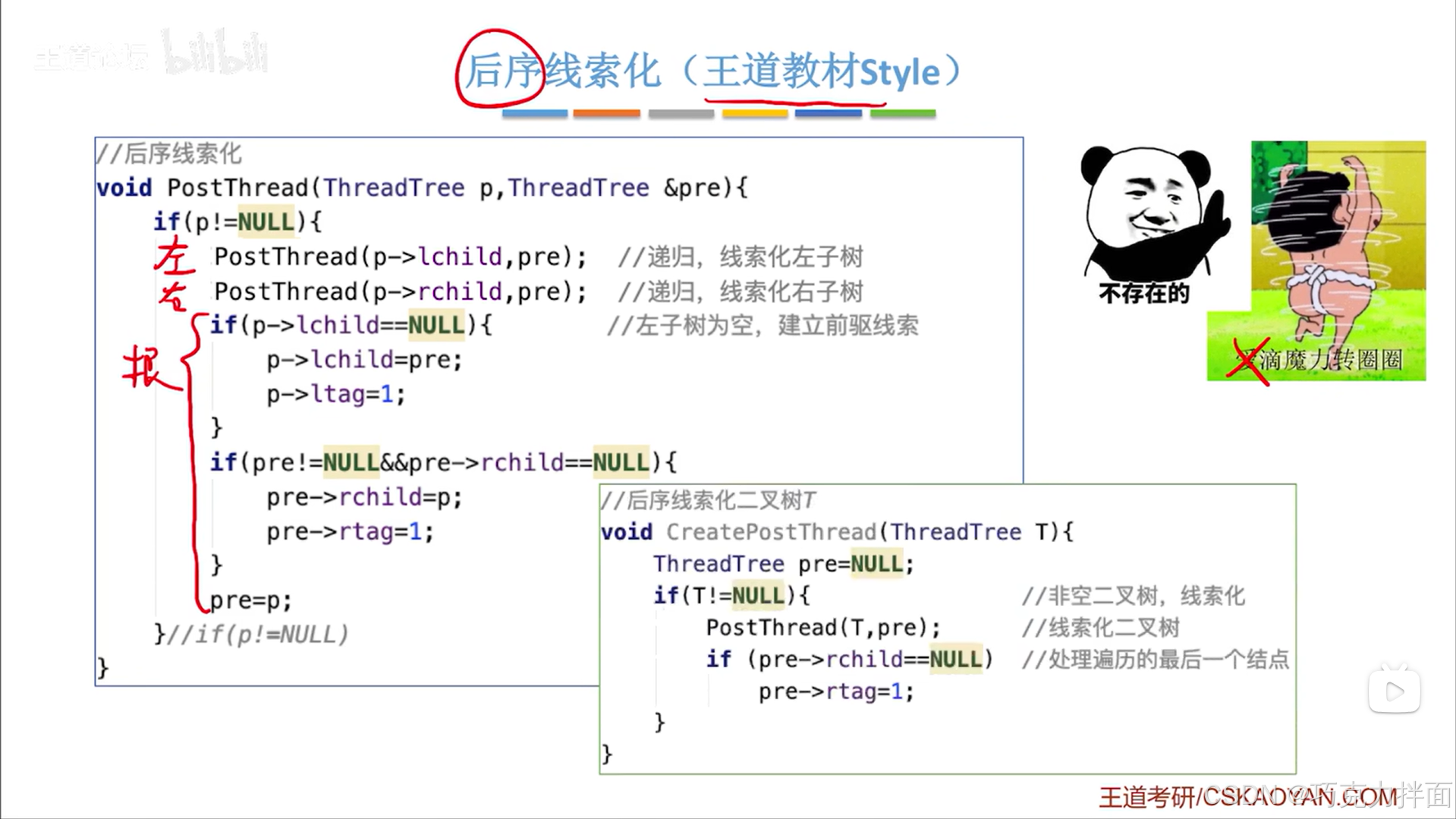
方案一:

方案二:
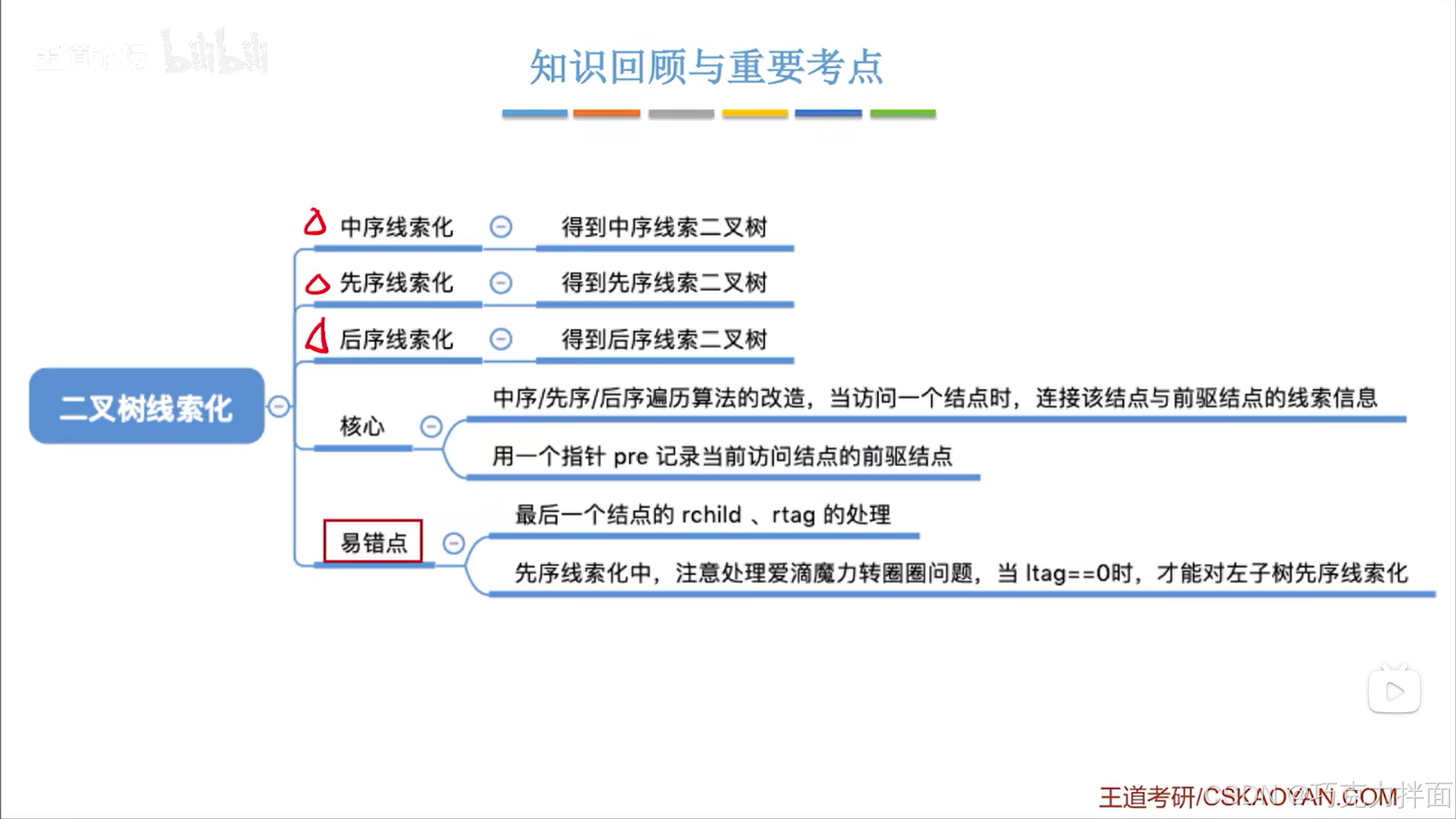
三.总结:
中序线索化和后续线索化不会出现先序线索化中循环访问结点的问题即"爱滴魔力转圈圈"问题,因为当访问一个结点时,无论中序遍历还是后序遍历,都已经对这个结点的左孩子指针处理完毕,所以访问完该结点时不可能再回头去访问该结点的左孩子指针所指向的内容





















 2006
2006

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








