一、神经网络学习算法的本质
- 当我们搭建好一个神经网络后,无论在什么应用场合,我们的目标都是:将网络的权值和偏置都变成一个最好的值,这个值可以让我们的输入得到理想的输出。
- 可能大家会觉的神经网络架构很非常神秘和复杂,其实任何一个神经网络架构都是一个多层复合的复合函数,我们可以将它们表示为:f(x,w,b)f(x,w,b)f(x,w,b),其中x是输入,www是权值,bbb为偏置。
- 我们的目标就变成了尝试不同的w,bw,bw,b值,使得最后的f(x,w,b)f(x,w,b)f(x,w,b)最接近我们的标签yyy。
- 现在我们需要一个指标来描述接近这个概念,于是产生了损失函数,这里我们将损失函数令为:(f(x,w,b)−y)2=C(w,b)(f(x,w,b)-y)^2=C(w,b)(f(x,w,b)−y)2=C(w,b),现在问题变成:将最小C(w,b)C(w,b)C(w,b)化。
- 将最小C(w,b)C(w,b)C(w,b)化这个问题,我们能够马上想到使用梯度下降算法。即:
- 第一步:求解梯度 [∂C(w,b)∂w1,∂C(w,b)(∂b1),∂C(w,b)∂w2,∂C(w,b)∂b2…,∂C(w,b)(∂wn),∂C(w,b)∂bn]=∂C(w,b)∂[W,b][\frac{∂C(w,b)}{∂w_1 },\frac{∂C(w,b)}{(∂b_1 )},\frac{∂C(w,b)}{∂w_2 },\frac{∂C(w,b)}{∂b_2 }…,\frac{∂C(w,b)}{(∂w_n )},\frac{∂C(w,b)}{∂b_n }]=\frac{∂C(w,b)}{∂[W,b]}[∂w1∂C(w,b),(∂b1)∂C(w,b),∂w2∂C(w,b),∂b2∂C(w,b)…,(∂wn)∂C(w,b),∂bn∂C(w,b)]=∂[W,b]∂C(w,b)
- 第二步:更新参数:[W,b]=[W,b]−η∂C(w,b)∂[W,b][W,b]=[W,b]-η\frac{∂C(w,b)}{∂[W,b]}[W,b]=[W,b]−η∂[W,b]∂C(w,b)其中ηηη为步长。
- 不断迭代上面两步直到函数C(w,b)C(w,b)C(w,b)不能再减少
- 这里解释以下梯度的含义:
- 对于任意一个多元函数f(x1,x2,…,xn)f(x_1,x_2,…,x_n)f(x1,x2,…,xn),它的梯度为: ∇f=[∂f∂x1,∂f∂x2,…,∂f∂xn]∇f=[\frac{∂f}{∂x_1 },\frac{∂f}{∂x_2},…,\frac{∂f}{∂x_n }]∇f=[∂x1∂f,∂x2∂f,…,∂xn∂f]
- 梯度的维度与函数变量维度是一样的,它表示如果自变量沿着梯度方向运动,函数fff的函数值将增长最快。当然反过来,如果沿着梯度的反方向函数值将减少最快,这也是为啥上面用减号。
- 其中∂f∂xi\frac{∂f}{∂x_i }∂xi∂f为函数fff对变量xix_ixi的偏导数,它的含义是其他变量不变的情况下xix_ixi增加1函数值的改变量,即函数相对xix_ixi的的变化率。
- 上面推导的过程的总结:网络权值和偏置更新问题⇒f(x,w,b)\Rightarrow f(x,w,b)⇒f(x,w,b)的结果逼近y⇒C(w,b)=(f(x,w,b)−y)2y\Rightarrow C(w,b)=(f(x,w,b)-y)^2y⇒C(w,b)=(f(x,w,b)−y)2取极小值问题 ⇒C(w,b)\Rightarrow C(w,b)⇒C(w,b)按梯度下降问题⇒\Rightarrow⇒取到极小值,网络达到最优
- 一切都是那么顺利,但是我们忘记了上面推导都是基于一个前提:我们已经提前知道损失函数在当前点的梯度。然而事实并非如此
- 这个问题困扰了NN研究者多年,1969年M.Minsky和S.Papert所著的《感知机》一书出版,它对单层神经网络进行了深入分析,并且从数学上证明了这种网络功能有限,甚至不能解决象"异或"这样的简单逻辑运算问题。同时,他们还发现有许多模式是不能用单层网络训练的,而对于多层网络则没有行之有效的低复杂度算法,最后他们甚至认为神经元网络无法处理非线性问题。然而于1974年,Paul Werbos首次给出了如何训练一般网络的学习算法—back propagation(BP)算法。这个算法可以高效的计算每一次迭代过程中的梯度,让以上我们的推导得以实现。不巧的是,在当时整个人工神经网络社群中无人知晓Paul所提出的学习算法。直到80年代中期,BP算法才重新被David Rumelhart、Geoffrey Hinton及Ronald Williams、David Parker和Yann LeCun独立发现,并获得了广泛的注意,引起了神经网络领域研究的第二次热潮。
二、梯度求解的链式法则
- 上面我们已经已经知道了梯度求解的公式: ∇f=[∂f∂x1,∂f∂x2,…,∂f∂xn]∇f=[\frac{∂f}{∂x_1 },\frac{∂f}{∂x_2},…,\frac{∂f}{∂x_n }]∇f=[∂x1∂f,∂x2∂f,…,∂xn∂f],并且我们也知道了中间的每个元素是函数对相应变量的偏导数∂f∂xi\frac{∂f}{∂x_i }∂xi∂f。我们也知道了偏导数的含义就是:函数相对xix_ixi的的变化率。
- 那么我们只要求出函数fff对每个变量的变化率,我们就可以求出函数fff的梯度,我们使用下面一个例子来说明这个问题。
- 假设有这样一个运算图:可以将其理解为一个简单的神经网络,eee为输出层,a,ba,ba,b为输入层,c,dc,dc,d为隐藏层。该网络可以表示为函数:e=f(a,b)=(a+b)∗(b+1)e=f(a,b)=(a+b)*(b+1)e=f(a,b)=(a+b)∗(b+1)

- 假设输入a=2,b=1a=2,b=1a=2,b=1,在这种情况下,如果只考虑相邻层的偏导关系,可以得到下图:

- 根据偏导的含义和上图可知:
- 如果如果其他变量不变,aaa改变1,那么ccc就会改变1,而ccc改变1,eee就会改变2,所有最后得到:aaa改变1,eee就会改变2,即eee相对aaa的变化率为2,即∂e∂a=2\frac{∂e}{∂a}=2∂a∂e=2
- 如果如果其他变量不变,bbb改变1,那么ccc就会改变1并且ddd也会改变1,而ccc改变1,eee就会改变2,ddd改变1,eee就会改变3,所有最后得到:bbb改变1,eee就会改变5,即eee相对aaa的变化率为5,∂e∂b=5\frac{∂e}{∂b}=5∂b∂e=5
- 上面这个过程就是链式法则,最后总结的公式为: ∂e∂a=∂e∂c∗∂c∂a\frac{∂e}{∂a}=\frac{∂e}{∂c}*\frac{∂c}{∂a}∂a∂e=∂c∂e∗∂a∂c∂e∂b=∂e∂c∗∂c∂b+∂∂d∗∂d∂a\frac{∂e}{∂b}=\frac{∂e}{∂c}*\frac{∂c}{∂b}+\frac{∂}{∂d}*\frac{∂d}{∂a}∂b∂e=∂c∂e∗∂b∂c+∂d∂∗∂a∂d由此可知∂e∂a\frac{∂e}{∂a}∂a∂e的值等于从aaa到eee的路径上的偏导值的乘积,而e∂b\frac{e}{∂b}∂be的值等于从bbb到eee的路径1(b−c−e)(b-c-e)(b−c−e)上的偏导值的乘积加上路径2(b−d−e)(b-d-e)(b−d−e)上的偏导值的乘积。
- 为啥要这样分析呢?最主要的原因是一般的神经网络的深度是较深的,我们直接去求去求某个损失函数对某个参数的偏导是比较困难的,但是求临近层变量之间的偏导数是非常容易的,通过链式法则,我们可以用临近层的偏导数来求解出损失函数对所有参数的偏导数。
三、前向神经网络中链式法则求解梯度
- 图是一个典型的前向神经网络或者叫全链接神经网络:Layer L1是输入层,Layer L2是隐含层,Layer L3是隐含层
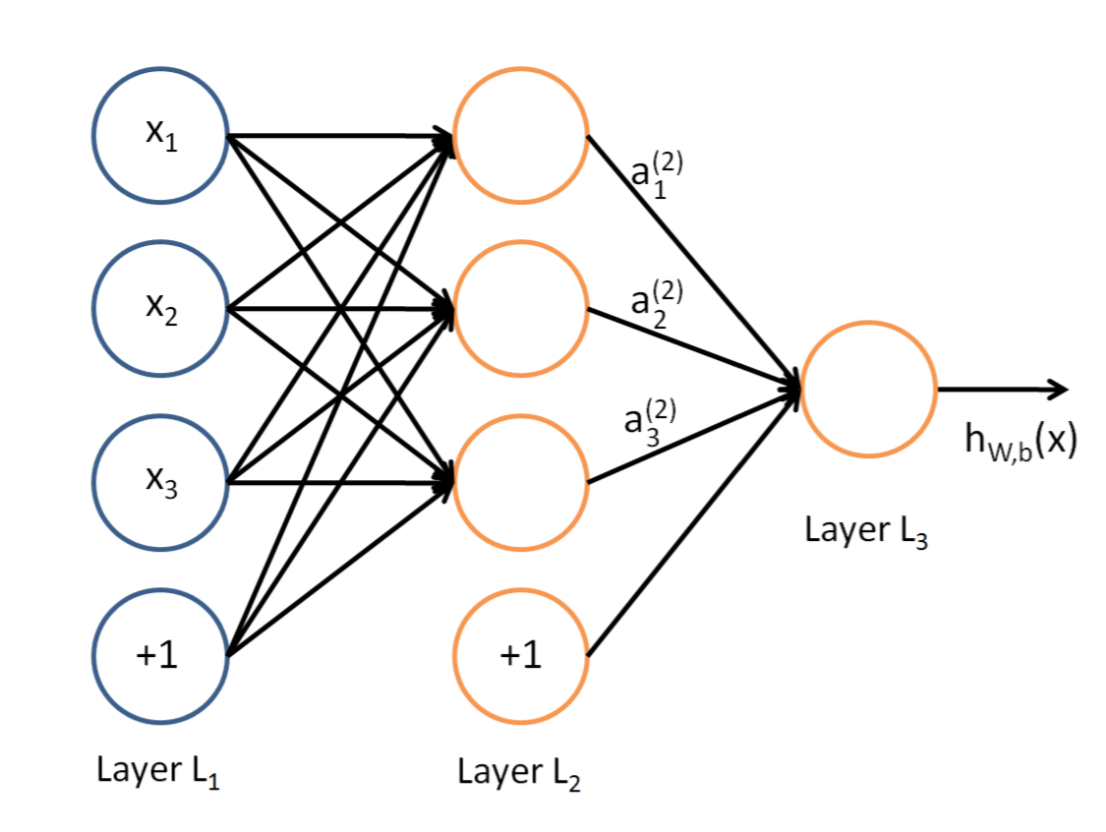
- 这一部分使用一个简单例子,来说明一下神经网络中梯度的求解过程,使用下面简单的网络:

- 输入层包含两个神经元i1,i2i_1,i_2i1,i2,和截距项b1b_1b1;隐含层包含两个神经元h1,h2h_1,h_2h1,h2和截距项b2b_2b2,输出层包含两个神经元o1,o2o_1,o_2o1,o2,每的权重我为wiw_iwi,激活函为sigmoid函数:sigmoid(x)=11+e−xsigmoid(x)=\frac{1}{1+e^{-x} }sigmoid(x)=1+e−x1导数为:sigmoid(x)=sigmoid(x)(1−sigmoid(x))sigmoid(x)=sigmoid(x)(1-sigmoid(x))sigmoid(x)=sigmoid(x)(1−sigmoid(x))
- 每个节点的运算关系用o1o_1o1做为一个例子进行说明一下:
- o1o_1o1输入(neto1net_{o1}neto1)为:neto1=outh1∗w5+outh2∗w6+b21net_{o1}=out_{h1}*w_5+out_{h2}*w_6+b_{21}neto1=outh1∗w5+outh2∗w6+b21
- o1o_1o1输出(outo1out_{o1}outo1)为:outo1=sigmoid(neto1)out_{o1}=sigmoid(net_{o1})outo1=sigmoid(neto1)
- 定义损失函数: Etotal=∑12(target−output)2E_{total}=∑\frac{1}{2} (target-output)^2 Etotal=∑21(target−output)2
- 我们需要更新的是权重www和偏置项bbb来最小化损失函数EtotalE_{total}Etotal,所有我们需要求出的是损失函数对www和bbb的梯度,即损失函数对每个权重wiw_iwi和每个偏置项bib_ibi的变化率(偏导数)。
- 求损失函数对于隐藏层到输出层的权重和偏置项的偏导数,我们用w5w_5w5和b21b_{21}b21来作为一个例子:
- 求损失函数EtotalE_{total}Etotal相对w5w_5w5的变化率的思路为:EtotalE_{total}Etotal相对o1o_1o1输出(outo1out_{o1}outo1)的变化率⇒o1\Rightarrow o_1⇒o1输出相对o1o_1o1输人(neto1net_{o1}neto1)的变化率⇒o1\Rightarrow o_1⇒o1输人相对w5w_5w5的变化率。
- 得到链式法则:∂Etotal∂w5=∂Etotal∂outo1∗∂outo1∂neto1∗∂neto1∂w5\frac{∂E_{total}}{∂w_5} =\frac{∂E_{total}}{∂out_{o1} }*\frac{∂out_{o1}}{∂net_{o1} }*\frac{∂net_o1}{∂w_5 }∂w5∂Etotal=∂outo1∂Etotal∗∂neto1∂outo1∗∂w5∂neto1
- 过程图如下:
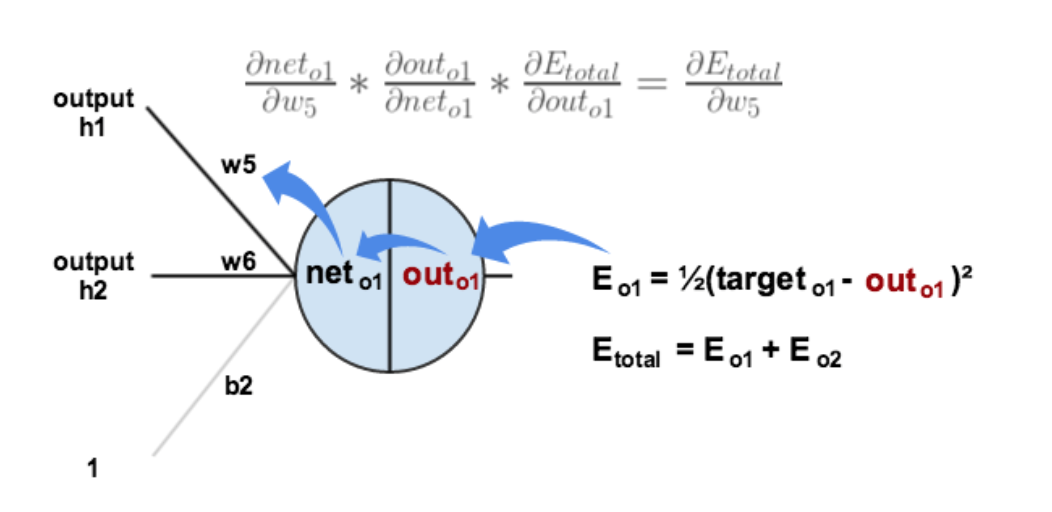
- 具体求导(根据每个量的表达式):∂Etotal∂outo1=(targeto1−outo1)\frac{∂E_{total}}{∂out_{o1}}=(target_o1-out_o1)∂outo1∂Etotal=(targeto1−outo1)∂outo1∂neto1=sigmoid(neto1)(1−sigmoid(neto1))=outo1(1−outo1)\frac{∂out_{o1}}{∂net_{o1}}=sigmoid(net_{o1} )(1-sigmoid(net_{o1} ))=out_{o1} (1-out_{o1})∂neto1∂outo1=sigmoid(neto1)(1−sigmoid(neto1))=outo1(1−outo1)∂neto1∂w5=outh1\frac{∂net_{o1}}{∂w_{5 }}=out_{h1}∂w5∂neto1=outh1
- 整理公式:∂Etotal)∂w5=(targeto1−outo1)∗outo1(1−outo1)∗outh1\frac{∂E_{total)}}{∂w_5 }=(target_{o1}-out_{o1} )*out_{o1} (1-out_{o1} )*out_{h1}∂w5∂Etotal)=(targeto1−outo1)∗outo1(1−outo1)∗outh1将前两项记为:δo1=∂Etotal∂outo1∗∂outo1∂neto1=∂Etotal∂neto1=(targeto1−outo1)∗outo1(1−outo1)δ_{o1}=\frac{∂E_{total}}{∂out_{o1}}*\frac{∂out_{o1}}{∂net_{o1}}=\frac{∂E_{total}}{∂net_{o1 }}=(target_{o1}-out_{o1} )*out_{o1} (1-out_{o1} )δo1=∂outo1∂Etotal∗∂neto1∂outo1=∂neto1∂Etotal=(targeto1−outo1)∗outo1(1−outo1)δo1δ_{o1}δo1表示的是:误差EtotalE_{total}Etotal相对于输入层o1(neto1)o_1(net_{o1})o1(neto1)的变化率
- 最后公式变为:∂Etotal∂w5=δo1∗outh1\frac{∂E_{total}}{∂w_5 }=δ_{o1}*out_{h1}∂w5∂Etotal=δo1∗outh1
- 我们用同样的方法来分析b21b_{21}b21: b_2的改变会影响o1o_1o1的输入,即neto1net_{o1}neto1,同时neto1net_{o1}neto1的变化必将影响outo1out_{o1}outo1,进一步outo1out_{o1}outo1的变化会影响损失函数EtotalE_{total}Etotal,于是可以得到链式法则:∂Etotal∂b21=∂Etotal∂outo1∗∂outo1∂neto1∗∂neto1∂b21\frac{∂E_{total}}{∂b_{21}}=\frac{∂E_{total}}{∂out_{o1}} *\frac{∂out_{o1}}{∂net_{o1}}*\frac{∂net_{o1}}{∂b_{21}}∂b21∂Etotal=∂outo1∂Etotal∗∂neto1∂outo1∗∂b21∂neto1
- 并且:∂neto1∂b21=1\frac{∂net_{o1}}{∂b_{21}}=1∂b21∂neto1=1
- 所以有:∂Etotal∂b21=∂Etotal∂outo1∗∂outo1∂neto1∗∂neto1∂b21=δo1\frac{∂E_{total}}{∂b_{21}}=\frac{∂E_{total}}{∂out_{o1}} *\frac{∂out_{o1}}{∂net_{o1}}*\frac{∂net_{o1}}{∂b_{21}}=δ_{o1}∂b21∂Etotal=∂outo1∂Etotal∗∂neto1∂outo1∗∂b21∂neto1=δo1
- 求损失函数对于输出层到隐藏层的权重和偏置项的偏导数,我们用w1w_1w1和b11b_{11}b11来作为一个例子:
- 方法其实与上面说的差不多,但是有个地方需要变一下,在上文计算损失函数对w5w_5w5的偏导时,导数传递的路径是:Etotal→outo1→neto1→w5E_{total}→out_{o1}→net_{o1}→w_5Etotal→outo1→neto1→w5
- 但是计算损失函数对w1w_1w1的偏导时,导数传递的路径有多条:Etotal→outo1→neto1→outh1→neth1→w1E_{total}→out_{o1}→net_{o1}→out_{h1}→net_{h1}→w_1Etotal→outo1→neto1→outh1→neth1→w1Etotal→outo2→neto2→outh1→neth1→w1E_{total}→out_{o2}→net_{o2}→out_{h1}→net_{h1}→w_1Etotal→outo2→neto2→outh1→neth1→w1
- 如下图所示:
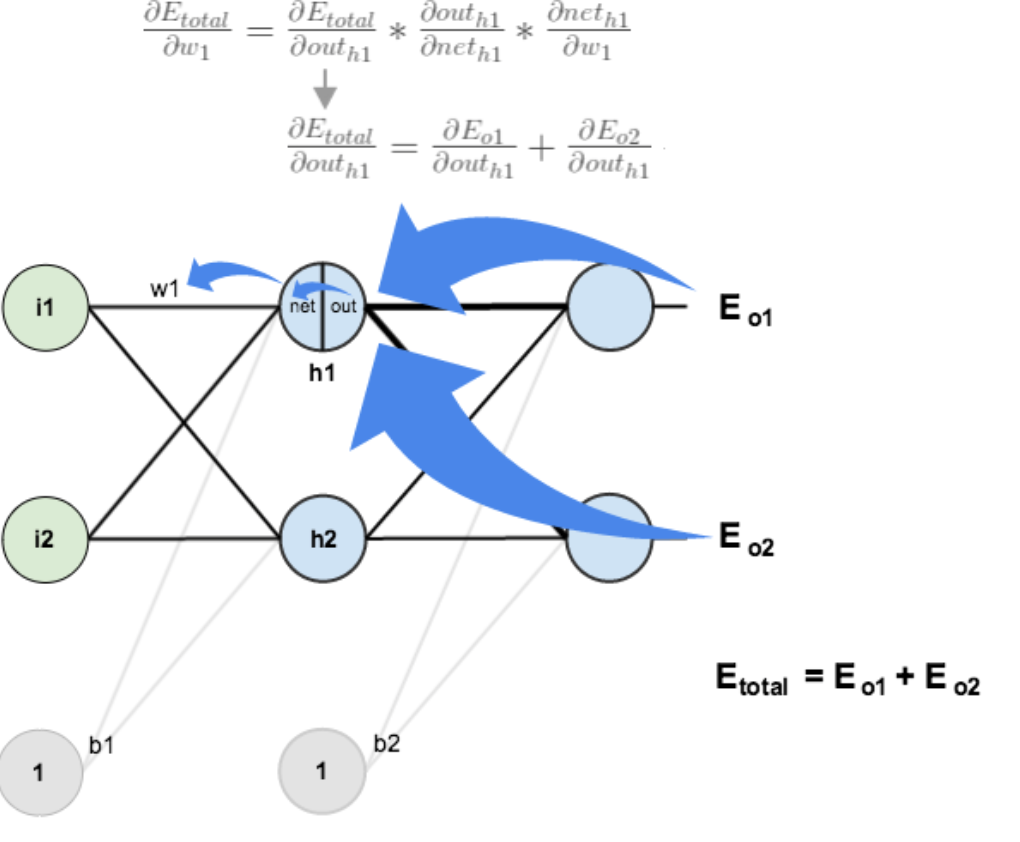
- 由上面的推导可知:Etotal→outo1→neto1=δo1E_{total}→out_{o1}→net_{o1}=δ_{o1}Etotal→outo1→neto1=δo1Etotal→outo2→neto2=δo2E_{total}→out_{o2}→net_{o2}=δ_{o2}Etotal→outo2→neto2=δo2
- 所以链式法则为:∂Etotal∂w1=(δo1∗∂neto1∂outh1+δo2∗∂neto2∂outh1)∗∂outh1∂neth1∗∂neth1∂w1\frac{∂E_{total}}{∂w_1}=(δ_{o1}*\frac{∂net_{o1}}{∂out_{h1}} +δ_{o2}*\frac{∂net_{o2}}{∂out_{h1}})*\frac{∂out_{h1}}{∂net_{h1}}*\frac{∂net_{h1}}{∂w_1 }∂w1∂Etotal=(δo1∗∂outh1∂neto1+δo2∗∂outh1∂neto2)∗∂neth1∂outh1∗∂w1∂neth1
- 现在一项一项求:∂neto1∂outh1=w5\frac{∂net_{o1}}{∂out_h1 }=w_5∂outh1∂neto1=w5∂neto1∂outh1=w7\frac{∂net_{o1}}{∂out_{h1}}=w_7∂outh1∂neto1=w7∂outh1∂neth1=sigmoid(neth1)(1−sigmoid(neth1))=outh1(1−outh1)\frac{∂out_{h1}}{∂net_{h1 }}=sigmoid(net_{h1} )(1-sigmoid(net_{h1} ))=out_{h1} (1-out_{h1})∂neth1∂outh1=sigmoid(neth1)(1−sigmoid(neth1))=outh1(1−outh1)∂neth1)∂w1=i1\frac{∂net_{h1)}}{∂w_1 }=i_1∂w1∂neth1)=i1
- 简化公式:δh1=∂Etotal∂neth1=(δo1∗∂neto1∂outh1+δo2∗∂neto2∂outh1)∗∂outh1∂neth1=(δo1∗w5+δo2∗w7)∗outh1(1−outh1)δ_h1=\frac{∂E_{total}}{∂net_{h1}} =(δ_{o1}*\frac{∂net_{o1}}{∂out_{h1} }+δ_{o2}*\frac{∂net_{o2}}{∂out_{h1}})*\frac{∂out_{h1}}{∂net_{h1 }}=(δ_{o1}*w_5+δ_{o2}*w_7 )*out_{h1} (1-out_{h1})δh1=∂neth1∂Etotal=(δo1∗∂outh1∂neto1+δo2∗∂outh1∂neto2)∗∂neth1∂outh1=(δo1∗w5+δo2∗w7)∗outh1(1−outh1)
- 所以最后公式为:∂Etotal∂w1=δh1i1\frac{∂E_{total}}{∂w_1 }=δ_{h1} i_1∂w1∂Etotal=δh1i1
- 我们用同样的方法来分析b11b_{11}b11得到链式法则:∂Etotal∂b1=δh1\frac{∂E_{total}}{∂b_1 }=δ_{h1}∂b1∂Etotal=δh1
- 根据上面的分析我们能求出神经网络上所有权重和偏置项的偏导数,即求出损失函数对整个网络参数的梯度。然后使用梯度下降法就能最小化损失函数,求出最佳网络。这就是神经网络的后向传播算法
四、后向传播算法
- 这一步主要是讲BP算法推广到一般的前向网络(全链接神经网络)当中去,并将公式进行了进一步简化。
- 前向神经网络的一般结构如下:)
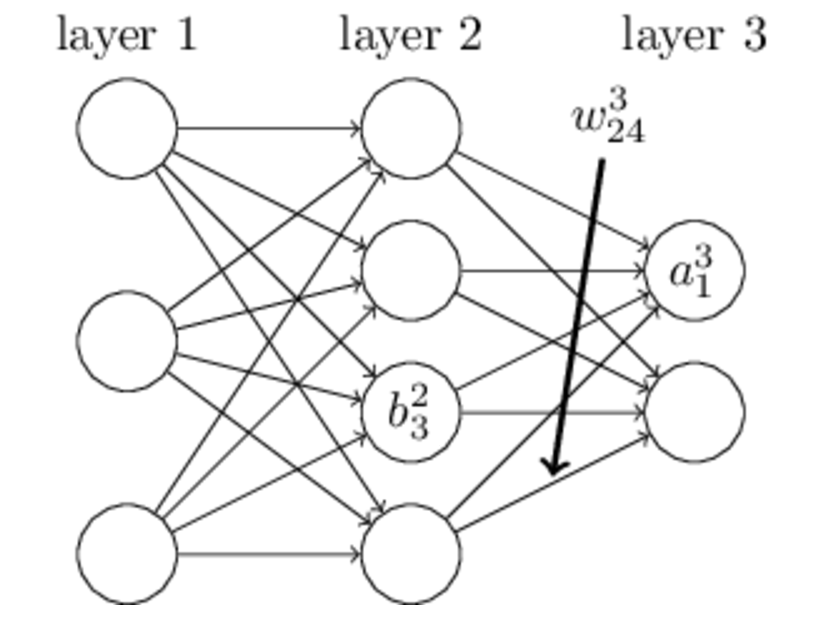
- 一些变量:
- 权重wjklw_{jk}^lwjkl:表示第l−1l-1l−1层的第kkk个神经元连接到第lll层的第jjj个神经元的权重;
- 偏置项bjlb_j^lbjl:表示第层lll的第个jjj神经元的偏置;
- 输入zjlz_j^lzjl:表示第lll层的第jjj个神经元的输入:zjl=∑kwjklakl−1+bjlz_j^l=∑_kw_{jk}^l a_k^{l-1}+b_j^l zjl=k∑wjklakl−1+bjl
- 输出ajla_j^lajl:表示第lll层的第jjj个神经元的输出:ajl=σ(zjl)a_j^l=σ(z_j^l)ajl=σ(zjl)其中σσσ为激活函数。
- 损失函数:C(w,b)C(w,b)C(w,b)
- 损失函数对对某一层某个神经元输入的偏导δjlδ_j^lδjl:δjl=∂C∂zjlδ_j^l=\frac{∂C}{∂z_j^l }δjl=∂zjl∂C
- 神经网络的最大层数:LLL
- 后向传播算法的公式:
- δjL=∂C∂zjL=∂C∂ajl∗σ′(zjL)δ_j^L=\frac{∂C}{∂z_j^L }=\frac{∂C}{∂a_j^l }*σ'(z_j^L )δjL=∂zjL∂C=∂ajl∂C∗σ′(zjL)其中∂C∂ajl\frac{∂C}{∂a_j^l }∂ajl∂C是由损失函数的具体形式给出的。
- δjl=(∑iwijl+1δil+1)∗σ′(zjl)δ_j^l=(∑_iw_{ij}^{l+1} δ_i^{l+1} )*σ'(z_j^l )δjl=(i∑wijl+1δil+1)∗σ′(zjl)
- ∂C∂wjkl=δjl∗ajl−1\frac{∂C}{∂w_{jk}^l }=δ_j^l*a_j^{l-1}∂wjkl∂C=δjl∗ajl−1
- ∂C∂bjl=δjl\frac{∂C}{∂b_j^l }=δ_j^l∂bjl∂C=δjl
- 最后使用梯度下降算法更新权重和偏置项,直到损失函数不能下降,得到最优网络。
 深度学习:详解后向传播(BP)算法
深度学习:详解后向传播(BP)算法





 本文介绍了神经网络学习算法的核心,重点讨论了后向传播(BP)算法。BP算法解决了多层神经网络中梯度计算的问题,通过链式法则计算损失函数对网络参数的梯度,从而利用梯度下降法优化网络。文中详细阐述了BP算法的原理,包括链式法则的应用以及在前向神经网络中的梯度求解过程。
本文介绍了神经网络学习算法的核心,重点讨论了后向传播(BP)算法。BP算法解决了多层神经网络中梯度计算的问题,通过链式法则计算损失函数对网络参数的梯度,从而利用梯度下降法优化网络。文中详细阐述了BP算法的原理,包括链式法则的应用以及在前向神经网络中的梯度求解过程。
















 1943
1943










