变换:
- 假设xxx为n维列向量,yyy维m维列向量,AAA维m×n的矩阵。有下面公式成立:Ax=yAx=yAx=y
- 在上面式子中,我们可以将矩阵AAA看作是Rn→RmR^n→R^mRn→Rm的一个函数(变换),他将n维向量空间中的向量(xxx)映射到m维向量空间中(yyy)。RnR^nRn为函数的定义域,RmR^mRm为函数的值域
- 展开:x=[x1,x2,…,xn]x=[x_1,x_2,…,x_n]x=[x1,x2,…,xn]A=[ξ1,ξ2,…,ξn] A=[ξ_1,ξ_2,…,ξ_n]A=[ξ1,ξ2,…,ξn]ξi=[ξi1,ξi2,…,ξim] ξ_i=[ξ_i^1,ξ_i^2,…,ξ_i^m]ξi=[ξi1,ξi2,…,ξim]则:Ax=x1ξ1+x2ξ2+⋯+xnξnAx=x_1 ξ_1+x_2 ξ_2+⋯+x_n ξ_nAx=x1ξ1+x2ξ2+⋯+xnξn
- 由展开式我们知道,矩阵AAA构成函数的值域,是由AAA的列向量张成的线性空间。
线性变换:
- 线性变换是一类满足线性条件的变换。所谓的线性条件就是:T(u+v)=T(u)+T(v)T(u+v)=T(u)+T(v)T(u+v)=T(u)+T(v)T(cu)=cT(u)T(cu)=cT(u)T(cu)=cT(u)
- 假设nnn维空间的标准正交基维:[e1,e2,…,en][e_1,e_2,…,e_n][e1,e2,…,en]ei=[0,0,…,1,…,0]∈Rn
e_i=[0,0,…,1,…,0]∈R^nei=[0,0,…,1,…,0]∈Rn则xxx表示为:x=x1e1+x2e2+⋯+xnenx=x_1 e_1+x_2 e_2+⋯+x_n e_nx=x1e1+x2e2+⋯+xnen
经过线性变换TTT变换:T(x)=T(x1e1+x2e2+⋯+xnen)T(x)=T(x_1 e_1+x_2 e_2+⋯+x_n e_n )T(x)=T(x1e1+x2e2+⋯+xnen)=x1T(e1)+x2T(e2)+⋯+xnT(en)=x_1 T(e_1)+x_2 T(e_2)+⋯+x_n T(e_n)=x1T(e1)+x2T(e2)+⋯+xnT(en)=[T(e1),T(e2),…,T(en)][x1,x2,…,xn]T=[T(e_1 ),T(e_2 ),…,T(e_n )] [x_1,x_2,…,x_n ]^T=[T(e1),T(e2),…,T(en)][x1,x2,…,xn]T - 令:A=[T(e1),T(e2),…,T(en)]A=[T(e_1 ),T(e_2 ),…,T(e_n )]A=[T(e1),T(e2),…,T(en)]T(x)=AxT(x)=AxT(x)=Ax
- 线性变换TTT可以理解为一个向量函数f(x)=yf(x)=yf(x)=y,xxx为n维向量,yyy为n维向量。Am×nA^{m×n}Am×n被称为是线性变换T的标准矩阵。
- 总结:每个矩阵都对应着一个线性变换。
几何中的线性变换:
- 为了更好的说明线性变换的几何含义,我们在二维情况下进行说明,下面矩阵被称为 2 维平面上的旋转矩阵:A=[cosφ−sinφsinφcosφ]A=\begin{bmatrix} cosφ & -sinφ \\ sinφ & cosφ \end{bmatrix}A=[cosφsinφ−sinφcosφ]
- 根据上面的推理有线性映射T与其对应:A=[T(e1),T(e2)]A=[T(e_1 ),T(e_2)]A=[T(e1),T(e2)]T(e1)=[cosφsinφ]T(e_1 )=\begin{bmatrix} cosφ \\ sinφ \end{bmatrix}T(e1)=[cosφsinφ]T(e2)=[−sinφcosφ]T(e_2)=\begin{bmatrix} -sinφ \\ cosφ \end{bmatrix}T(e2)=[−sinφcosφ]e1=[10]e_1=\begin{bmatrix} 1 \\ 0 \end{bmatrix}e1=[10]e2=[01]e_2=\begin{bmatrix} 0 \\ 1 \end{bmatrix}e2=[01]
- 可以看出矩阵AAA的变换就是一个旋转操作,旋转图如下:
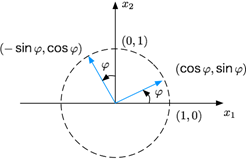





 本文探讨了矩阵作为线性变换的表示,解释了如何通过矩阵将n维向量映射到m维空间,并阐述了线性变换的性质。特别地,通过2维旋转矩阵的示例,展示了线性变换在几何中的直观意义。
本文探讨了矩阵作为线性变换的表示,解释了如何通过矩阵将n维向量映射到m维空间,并阐述了线性变换的性质。特别地,通过2维旋转矩阵的示例,展示了线性变换在几何中的直观意义。
















 603
603

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








