2_foc转速环_电磁转矩方程与运动方程的传递函数

        转速环里面包含有电流环在内，当外面给定转速时，系统通过控制iq来控制电磁转矩，从而电机开始转动。电机在转动的过程，传感器检测到机械角度会改变，也就是说电角度也会改变，由电角度在单位时间的变化，就可以求出电角速度，从而就可以得到反馈回来转速参与转速决策，最终可以控制转速稳定。

1、电磁转矩方程与运动方程的传递函数

网上的结构框图如下：

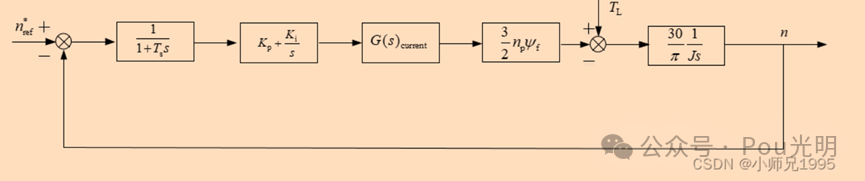
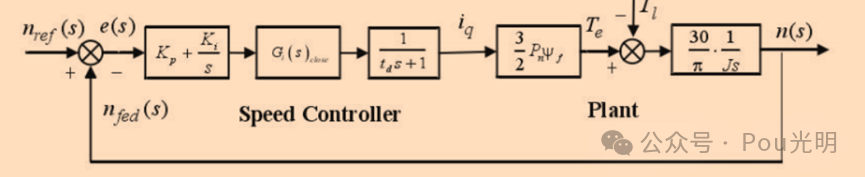
通过之前的学习，上面三种框图组成部分可分为速度环PI控制器、系统延迟、电流环、PMSM电磁转矩方程、PMSM运动方程。

①电磁转矩方程

1_FOC电流环_PI控制器参数整定_1

这里面有提到，对于表贴式，Ld=Lq=Ls；若为了实现为了实现最大扭矩控制，就会采用 𝑖𝑑=0 控制(后续再整理)，则：

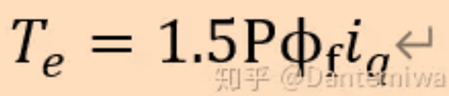
在框图中，iq来自之前的电流环。

①   运动方程

GPT:

1.1基本方程

首先，从电磁转矩 TeT_eTe和转子速度 ωr 的关系出发。

    1>电磁转矩

    PMSM的电磁转矩Te表达式为：

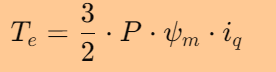
其中：

P是电机的极对数

ψm是永磁体的磁链

iq是q轴电流分量

2>机械运动方程

   机械运动方程描述了电磁转矩 Te与转子速度ωr之间的关系：

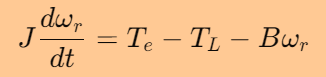
其中：

J是转动惯量

TL是负载转矩

B是粘性阻尼系数

在频域中，上述方程可以表示为：

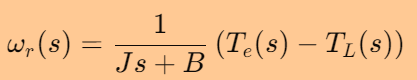
将电磁转矩 Te的表达式代入上式，可以得到：

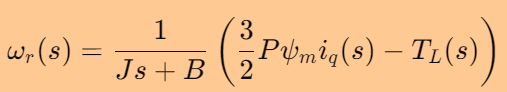
3>简化粘性阻尼项

通常假设阻尼项 B较小或可以忽略，这样机械运动方程进一步简化为：

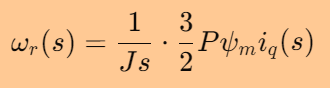
1. 2传递函数推导

假设在控制设计中，负载转矩 TLT_LTL 是已知且恒定值，因此可以考虑在推导过程中忽略它的动态变化。此时，传递函数仅由电流到转速的关系决定。

将电磁转矩与电流的关系代入，得到：

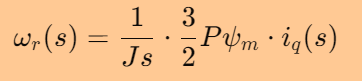
将上式中的常数项提取出来

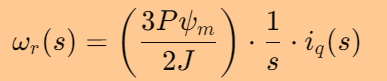
1. 3确定传递函数中的常数项

对于具体的传递函数，通常通过引入相应的常数因子将转速的单位从机械角速度（弧度/秒）转换为转速（RPM）。

机械角速度 ωr 和电机转速 n (单位: RPM) 之间的关系为：

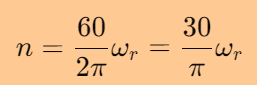
因此，上述传递函数可以表示为：

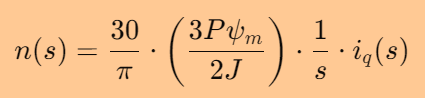
即：

1. 4结论

最终，PMSM在FOC控制中的传递函数，表示为输入电流 iq(s)和输出转速n(s)的关系：

1_FOC电流环_PI控制器参数整定_1

1_FOC电流环_PI控制器参数整定_2

2_foc开环控制详细流程

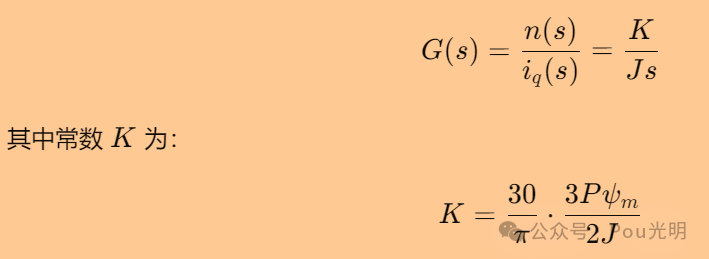
欢迎关注：