3_1_PID控制原理

       自从计算机进入控制领域以来，用数字计算机代替模拟计算机调节器组成计算机控制系统，不仅可以用软件实现PID控制算法，而且可以利用计算机的逻辑功能，使PID控制更加灵活。数字PID控制在生产过程中是一种最普遍采用的控制方法，在机电、冶金、机械、化工等行业中获得了广泛的应用。将偏差的比例(P)、积分(I)和微分(D)通过线性组合构成控制量，对被控对象进行控制，故称PID控制器。

       1.1 PID控制原理

       在模拟控制系统中，控制器最常用的控制规律是PID控制。模拟PID控制系统原理框图如下。系统由模拟PID控制器和被控对象组成。

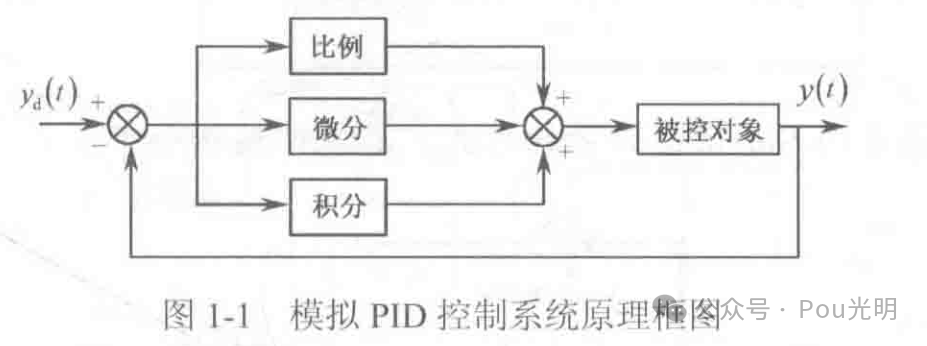
       PID控制器是一种线性控制器，它根据给定值yd(t)与实际输出值y(t)构成控制篇差：

       error(t) = yd(t) – y(t)                                               （1.1）

       PID控制规律为：

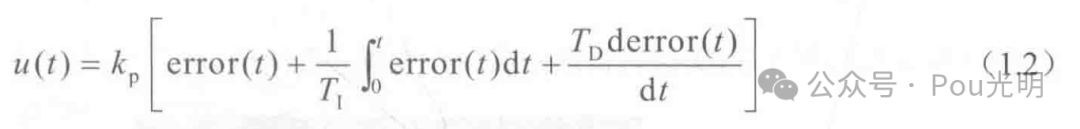
或写成传递函数的形式：    

        

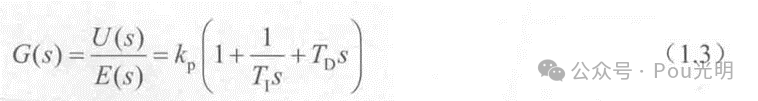
式中，kp为比例系数；T1为积分时间常数；T_D为微分时间常数。

       简单来说，PID控制器各校正环节的作用如下：

(1)比例环节：成比例地反映控制系统的偏差信号error(t)，偏差一旦产生，控制器立即产生控制作用，以减小偏差。

(2)积分环节：主要用于消除静差，提高系统的无差度。积分作用的强弱取决于积分时间常数T1，T1越大，积分作用越弱，反之则越强。

(3)微分环节：反映偏差信号的变化趋势(变化速率)，并能在偏差信号变得太大之前，在系统中引入一个有效的早期修正信号，从而加快系统的动作速度，减少调节时间。

       1.2  Matlab对阶跃信号的仿真

       代码：

%设一被控对象G(s)=50/(0.125s^2+7s)<em id="__mceDel">%用增量式PID控制算法编写仿真程序
%输入分别为单位阶跃、正弦信号，采样时间为1ms
 
clear;
close all;
ts=0.001;                 %采样时间
sys=tf(50,[0.125,7,0]); %tf是传递函数  即被控对象函数G（）;
dsys=c2d(sys,ts,'z');    %把控制函数离散化
[num,den]=tfdata(dsys,'v');% 离散化后提取分子、分母
u_1=0;
u_2=0;
y_1=0;
y_2=0;
error_1=0;
error_2=0;
P=0;I=0;D=0;
n=1000;
time=zeros(1,n);
rin=zeros(1,n);
yout=zeros(1,n);
for k=1:n
    time(k)=k*ts;                   %采样时间
    S=1;
    if S==1
        kp=10;ki=100;kd=0.1;        %初始化PID
        rin(k)=1*(time(k)>0.1);     %Step Signal
    elseif S==2
        kp=10;ki=100;kd=0.1;
        rin(k)=0.5*sin(2*pi*k*ts);  %Sine Signal即实际输入
    end
    du=kp*P+kd*I+ki*D;              %PID Controller控制系数
    u=u_1+du;                       %Restricting the output of controller
     
    yout(k)=-den(2)*y_1-den(3)*y_2+num(2)*u_1+num(3)*u_2;   %实际输出
    error=rin(k)-yout(k);           %Return of parameters 误差
    u_2=u_1;                        %保存上上次输入
    u_1=u;                          %保存上一次控制系数
    y_2=y_1;                        %保存上上次输出
    y_1=yout(k);                    %保存上一次输出
    P=error-error_1;                %Calculating P
    D=error-2*error_1+error_2;      %Calculating D
    I=error;                        %Calculating I
    error_2=error_1;                %保存上上次误差
    error_1=error;                  %保存上一次误差
end
figure;
plot(time,rin,'b',time,yout,'r');   %输入和实际控制输出
xlabel('time(s)'),ylabel('rin,yout');

       效果：    

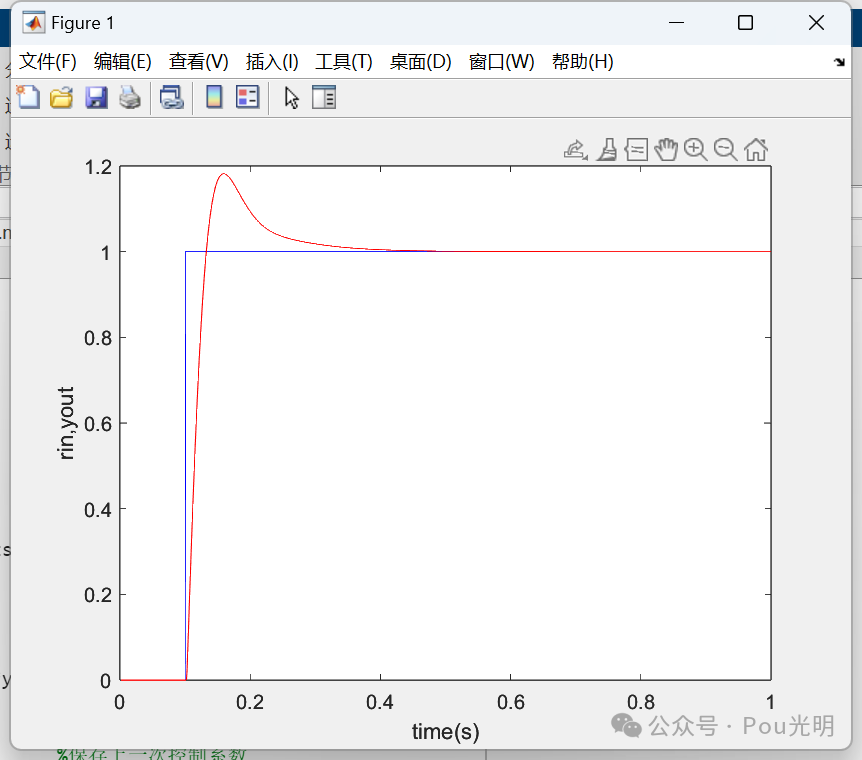
上面代码没研究，有兴趣的小伙伴可以研究修改测下。

Simulink PID仿真：

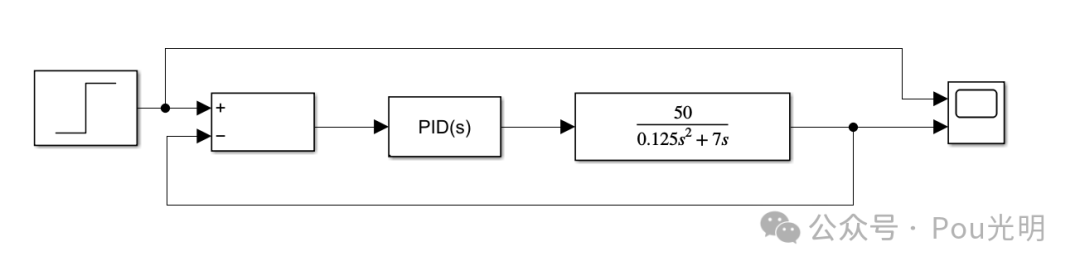
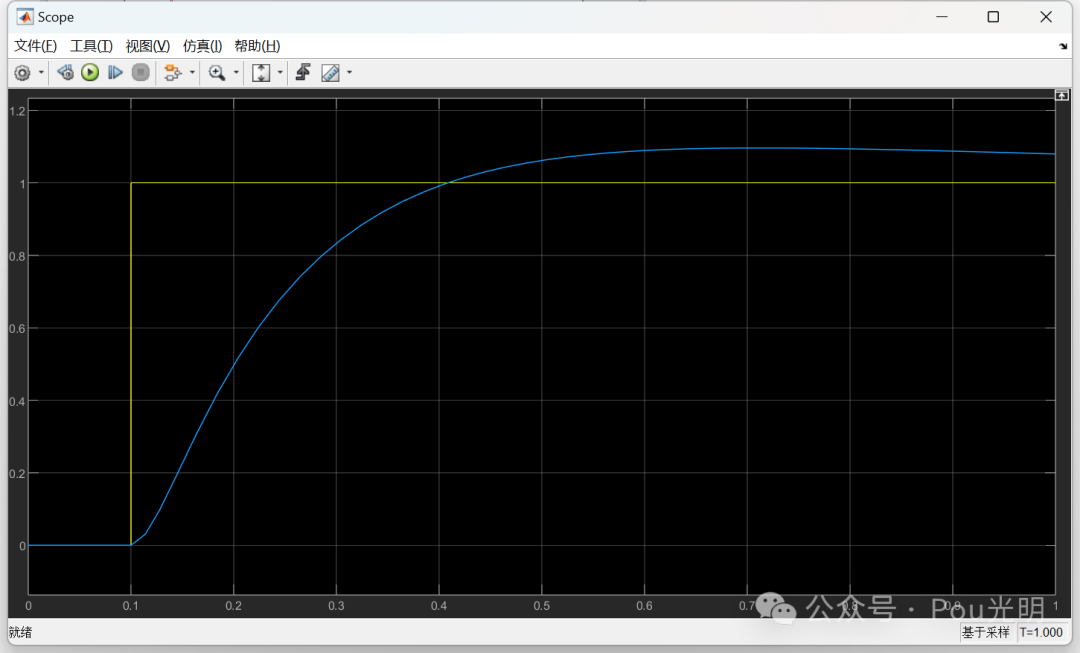
效果：    

《先进PID控制MATLAB仿真》

https://www.cnblogs.com/dingdangsunny/p/17967886

https://blog.youkuaiyun.com/STM89C56/article/details/105666186

欢迎关注：

有需要交流的小伙伴可留言讨论。