第8周：降维

降维：第二种类型的无监督学习问题
有几个不同的原因需要做降维。

1.动机一：数据压缩

不仅允许我们压缩数据，使用较少的计算机内存或磁盘空间，也让我们加快学习算法。

2.动机二：数据可视化

降维的算法只负责减少维数，新产生的特征的意义，就必须由我们自己去发现了。

假使我们有有关于许多不同国家的数据，每一个特征向量都有 50 个特征（如， GDP，人均 GDP，平均寿命等）。如果要将这个 50 维的数据可视化是不可能的。使用降维的方法将其降至 2 维，我们便可以将其可视化了

有待补充老师是如何降维的

3.主成分分析（PCA）：最常见的降维算法

找到一个方向向量，当我们把所有的数据都投射到该向量时，我们希望投射平均均方误差尽可能小。
方向向量是一个经过原点的向量，而投射误差是从特征向量向该方向向量作垂线的长度。

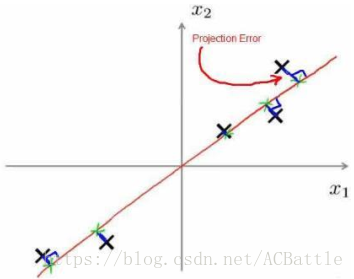
具体描述:
问题：将n维数据降至K维；
目标：找到向量$μ^1$,$μ^2$…$μ^k$,使得总的投射误差最小；
主成分分析与线性回归的比较：

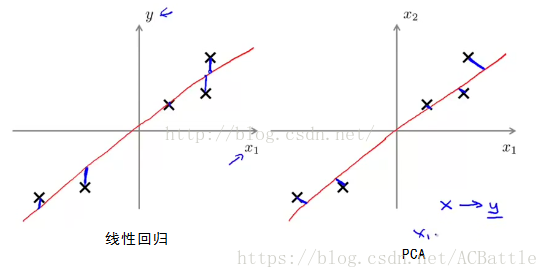
1）PCA最小化的是投射误差，线性回归尝试的是最小化预测误差。
2）线性回归的目的的预测结果，而PCA分析不做预测。
图像处理领域的KL变换使用PCA做图像压缩。但PCA要保证降维后数据的特性损失最小。
PCA技术的优缺点：
1）一大好处就是对数据进行降维处理。可以对新求出的“主元”向量的重要性进行排序，根据需要取前面最重要的部分，将后面的维数省去，可以达到降维从而简化模型或是对数据进行压缩的效果。同时最大的程度保持了原有数据的信息。
2）完全无参数限制。在计算过程中，完全不需要认为的设定参数或者根据任何经验模型对计算进行干预，最后的结果只与数据相关，与用户是独立的。
3）缺点：2）有可能也是缺点。如果用户对观测对象有一定的先验知识，掌握了数据的一些特征，却无法通过参数化等方法对处理过程进行干预，可能会得不到预期的效果，效率也不高。

4.PCA分析算法

1）均值归一化
计算出所有特征的均值，然后令$x_j$=$x_j$-$μ_j$。如果特征是在不同的数量级上，我们还需要除以标准差$σ^2$。
2）计算协方差矩阵Σ
Σ = $\frac{1}{m}$$\displaystyle\sum_{i=1}^{n}$($x^i$)$($$x^i$$)^T$
3）计算协方差矩阵的特征向量

Σ = $\frac{1}{m}$$\displaystyle\sum_{i=1}^{n}$($x^i$)$($$x^i$$)^T$
对于一个n×n维度的矩阵，上式中的U是一个具有与数据之间最小投射误差的方向向量构成的矩阵。如果我们希望将数据从n维降至K维，我们只需要从U中选取前K个向量，获得一个n×k维的矩阵，用$U_{reduce}$表示，然后通过如下计算获得要求的新特征向量$Z^i$：$Z^i$=$U_{reduce}^T$×$x^i$
其中x是n×1维的，因此结果为k×1维。

5.选择主成分的数量

主要成分分析是减少投射的平均均方误差：
训练集的方差为：$\frac{1}{m}$$\displaystyle\sum_{i=1}^{m}$$||$$x^i$$||^2$
我们希望在平均均方误差与训练集方差的比例尽可能小的情况下选择尽可能小的K值。
我们希望这个比例小于 1%，就意味着原本数据的偏差有 99%都保留下来了，如果我们选择保留 95%的偏差，便能非常显著地降低模型中特征的维度了。我们可以先令 k=1，然后进行主要成分分析，获得$U_{reduce}$和 z，然后计算比例是否小于1%。如果不是的话再令 k=2，如此类推，直到找到可以使得比例小于 1%的最小 k 值（原因是各个特征之间通常情况存在某种相关性）。
还有一个更好的方式来选择k，当我们在Octave中调用“svd”函数的时候，我们获得三个参数：[U,S,V] = svd(sigma)。



这部分没看懂，直接截的图，到时候看懂了，转换为文字。

6.重建的压缩表示

在那里你可能需要把1000维的数据压缩100维特征，或具有三维数据压缩到一二维表示。所以，如果这是一个压缩算法，应该能回到这个压缩表示，回到你原有的高维数据的一种近似。
所以，给定的$z^i$，这可能100维，怎么回到你原来表示的$x^i$，这可能是1000维的数组？
待补充，未看懂

7.主成分分析法的应用建议

举个栗子：
假使我们正在针对一张 100×100 像素的图片进行某个计算机视觉的机器学习，即总共有 10000 个特征。
* 运用主要成分分析将数据压缩至1000个特征；
* 对训练集运行学习算法；
* 在预测时，采用之前的学习而来的$U_{reduce}$将输入的特征x转换成特征向量z，然后再进行预测。

---

注意：
如果我们有交叉验证集 和 测试集，也采用训练集学习而来的$U_{reduce}$.

---

常见的错误的主要成分分析分析情况：
1）将其用于减少过拟合（减少了特征的数量）。这样做非常不好，不如尝试正则化处理。原因在于主要成分分析只是丢掉一些特征，它并不考虑任何与结果变量有关的信息，因此可能会丢失非常重要的特征。（详见）然而当我们进行正则化处理时，会考虑到结果变量，不会丢掉重要的数据。
2）默认地将主要成分分析作为学习过程的一部分，这虽然很多时候有效果，最好还是从所有原始特征开始，只在有必要的时候（算法运行太慢或者占用太多内存）才考虑采用主成分分析。