新型纳米机电开关设计与仿真

面向低功耗应用的一种新型纳米机电开关的设计、建模与仿真

一、引言

NANOELECTROMECHANICAL 系统（纳米机电系统）因其优异的特性已在逻辑应用领域得到研究[1]–[7]。由于在非工作状态下通过空气间隙隔离，纳米机电系统开关几乎无电流泄漏，也无亚阈值导通，从而降低了静态功耗。纳米机电系统开关可在极端温度和高辐射强度环境中运行[2]。因此，纳米机电系统是适用于超低功耗、中等速度系统的理想器件候选，可在其他技术失效的灾难环境中正常运行。

在[2]中提出了一种四端继电器设计，该继电器可模拟互补金属氧化物半导体中的n沟道和p沟道。在[6]中展示了一种测试器件，其电压摆幅为10 V。在[1]中提出了一种基于继电器解析模型的缩放理论，预测在低于100 MHz下工作的电路中，纳米机电系统相较于互补金属氧化物半导体可节省10倍的能量。文献[3]和[4]中提出的继电器器件通过理想的导通状态/关断状态模型进行了分析[1]–[3]。

本文讨论了一种新型基于纳米机电系统（NEMS）的 “异或门”和“或门”器件的制造与建模，这些器件根据宏功能切换其状态，从而实现更高的并行性，并减少实现逻辑功能所需的器件数量。例如，采用所提出的方法，基于NEMS的现场可编程门阵列（FPGA）可配置逻辑块（CLB）仅需使用八个纳米机电系统开关即可配置实现七种基本功能之一，而传统方法则需要上百个开关[8]。

本文还首次提出了一种纳米机电系统（NEMS）设计环境，该环境由机械集总模型和电路模型组成。该设计环境源自有限元分析（FEA）COMSOL 多物理场模型。有限元分析模型复现了所制造的纳米机电系统的实验测量结果。利用该设计环境，我们对纳米机电系统与互补金属氧化物半导体（CMOS）电路的功耗进行了比较。

第二节讨论了纳米机电系统器件的结构和制造步骤。第三节阐述了使用纳米机电系统器件设计数字逻辑门和存储器的方法。第四节介绍了三维有限元物理器件模型。第五节讨论了电路仿真模型的开发、物理特性提取过程，并展示了纳米机电系统逻辑门的仿真结果。第六节解释了功耗研究的实验设置和结果。结论在第七节中给出。

II. 纳米机电系统器件设计与制造

A. 纳米机电系统器件设计

此处考虑的纳米机电系统是一种具有四个端子的金属器件，如图1所示。它由两个在中心附近交叉的桥结构组成。输入门 G1和源极S触点位于上桥（桥1）上，而输入栅极G2和漏极D触点位于下桥（桥2）上。当G1与G2之间的电势差小于吸合电压（Vpull−in)时，S和D彼此不接触。在此状态下，器件关闭，S与D之间没有导电通路。当G1与G2之间的电势差超过Vpull−in时，器件开启。因此，仅当栅极G1或G2其中一个处于“1”状态时，该器件才会开启，使其成为异或逻辑门。

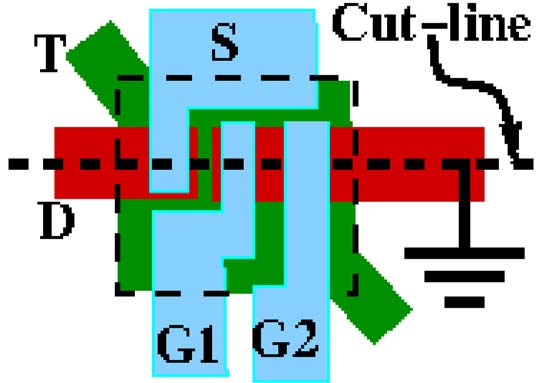
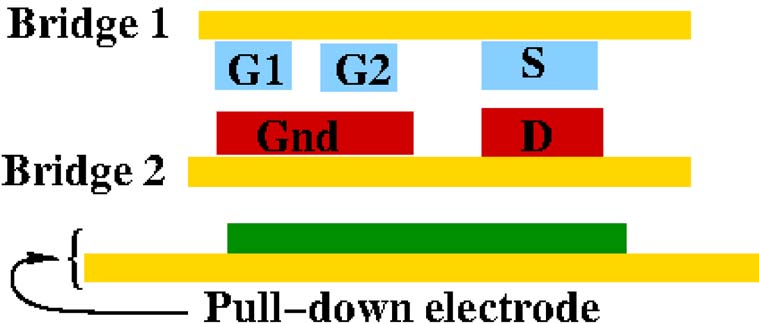
同样，图1(c)和(d)展示了或器件的顶部和横截面视图，该器件也包含两个桥结构，类似于异或器件，但栅极电极的排列方式不同，并增加了一个始终处于“0”电位的接地电极。在这种情况下，G1、G2和S位于桥1上，而接地（Gnd）和D电极位于桥2上。当G1与Gnd之间的电势差以及G2与Gnd之间的电势差均小于Vpull−in时，S和D接触不相互接触。当G1与Gnd之间或G2与Gnd之间的电势差大于Vpull−in时，器件被导通（即S与D接触）。当G1和G2上的输入电压中至少有一个为高电平时，该开关导通，构成或逻辑门。这些异或门和或门开关构成了纳米机电系统数字逻辑和现场可编程门阵列设计的基本构建单元。请注意，为了防止异或门中栅极之间以及或门中栅极与接地之间的漏电流，使用了一层薄绝缘层。

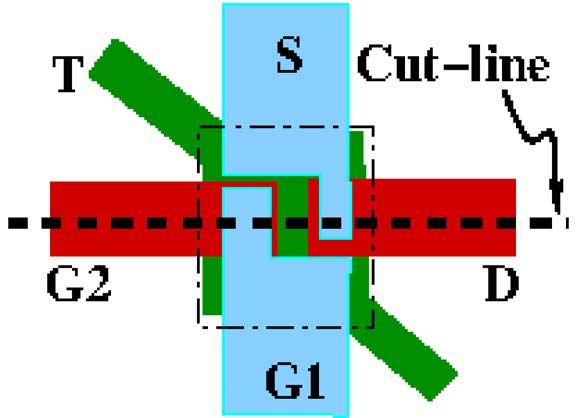异或纳米机电系统的顶视图。(b)异或纳米机电系统的横截面视图。(c)或纳米机电系统的顶视图。(d)或纳米机电系统的横截面视图。)

B. 器件制造

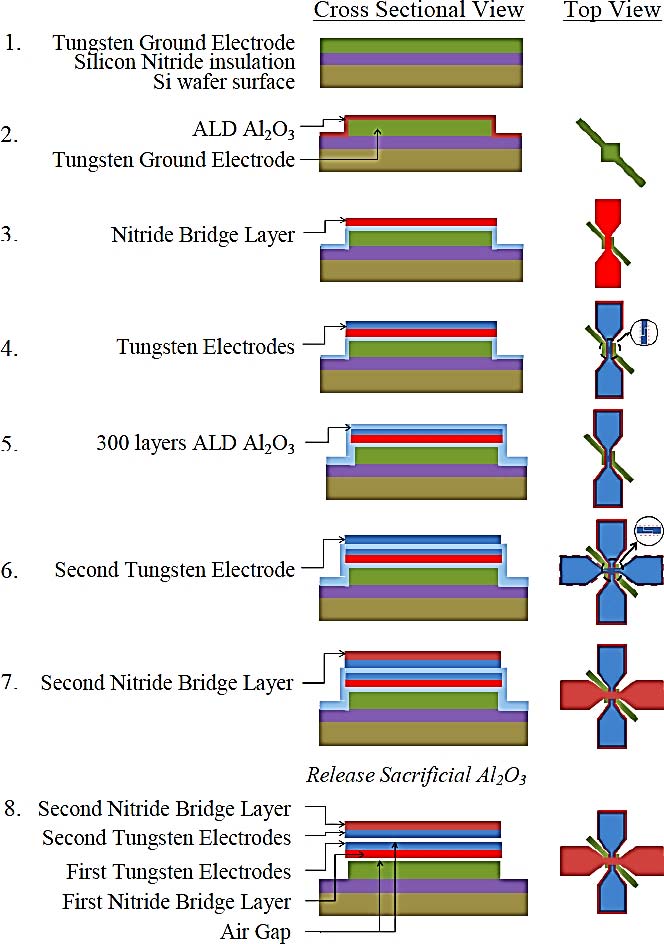
本文开发和讨论的仿真环境具有很强的通用性，可适用于多种不同类型的纳米/微米机电系统器件。本文展示了一个实验示例及其结果，以证明功能型纳米机电系统器件的可行性，以及利用单器件结构设计和制造逻辑门的可能性。该器件的制造工艺流程如图2所示，并在[9]和[10]中进行了详细讨论。导电硅片采用在780°C下通过低压化学气相沉积法沉积的100纳米化学计量氮化硅进行绝缘；首先，均匀溅射一层钨层（厚度100纳米）并进行图形化，以形成接地电极。该电极既可用于器件类似“MOSFET” 的操作中的栅极，也可在需要时用于分离两个桥结构。随后，用100层（∼0.1纳米/层）热法 Al2O3采用Fiji原子层沉积（ALD）系统沉积，随后沉积并图形化第二层化学计量LPCVD氮化物（100纳米），以形成第一个氮化物桥（图1中的桥2）。然后，通过溅射沉积第二层钨并进行图形化，在桥2上形成电极。接着使用 ALD Al2O3覆盖已图形化的钨层，并作为底部和顶部桥之间的牺牲间隙。接下来进行第三次钨金属化并图形化，以在桥1（图1中的上桥）上形成电极。然后，再使用另一层图案化的化学计量氮化物层来定义桥1。在完成需要八种掩模的整个结构制造后，使用缓冲氧化物刻蚀液对10 纳米ALD层进行牺牲性刻蚀，以“释放”两个桥结构彼此之间以及与衬底之间的连接。尽管桥的表面积（18×30μ m2）相当大，但由于存在图案化金属电极，即使具有非常大的高宽比，仍可实现ALD层的快速刻蚀。在室温下使用 H2O2作为湿法刻蚀剂对钨进行图形化，实现了在整个晶圆范围内干净且均匀的刻蚀。采用CF4/O2在200瓦条件下的干法刻蚀工艺对氮化硅进行图形化，从而实现了氮化物桥的干净刻蚀。ALD Al2O3层在此干法刻蚀工艺中起到了有效的刻蚀阻挡层作用。

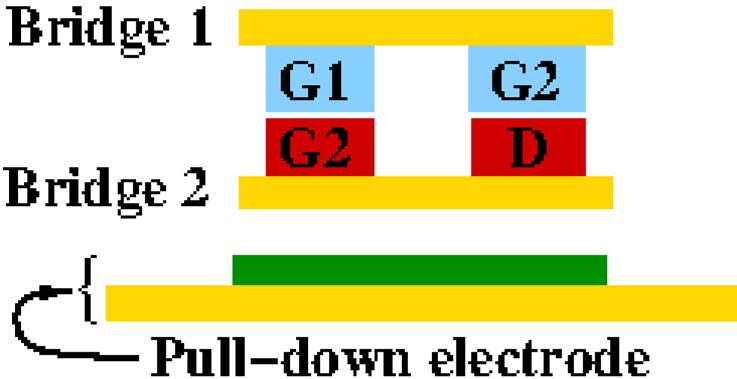
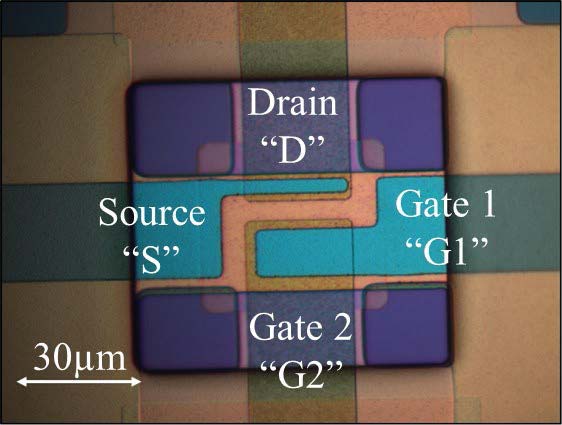
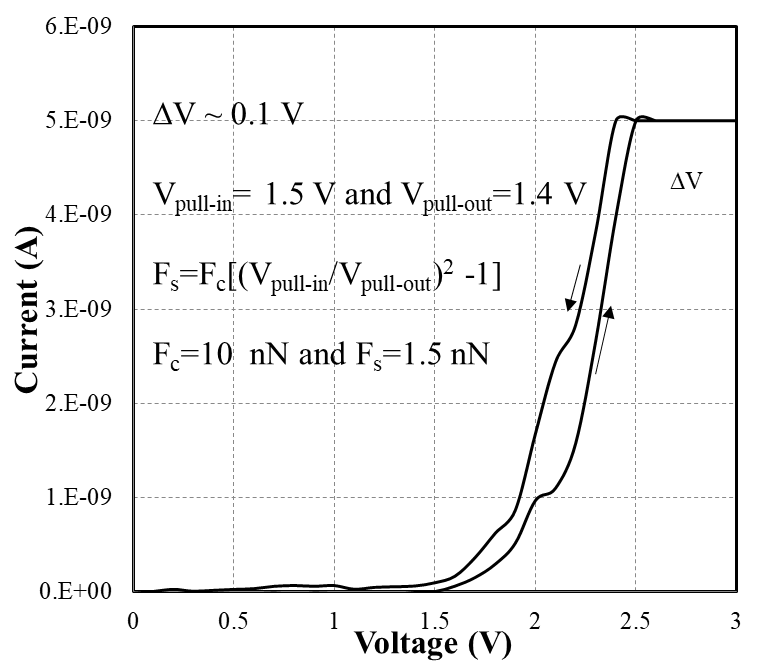
图3展示了微加工异或和或门器件的照片。传统异或门实现使用八个独立开关。图3(e)显示了一个采用光刻和聚焦离子束图案化工艺制造的镍基NEMS开关。器件数量减少八倍，同时运动部件数量和面积相应减少，从而提高了可靠性，门速度至少提高4倍，良率也成比例提升。此外，还可利用交叉桥几何结构设计多输入（>2）门，通过两条或更多金属走线实现多个接触电极。四输入异或门可将器件数量压缩至 ×24。该开关的I–V特性为如图3(f) 所示。 Vpull−in为 ∼1.5 V，迟滞约为 0.1 V。

Vpull−in与释放电压（Vpull−out）之间的差异可归因于粘附力（Fs），该器件的粘附力约为 1.5 nN（恢复悬臂梁的力为 10 nN）。

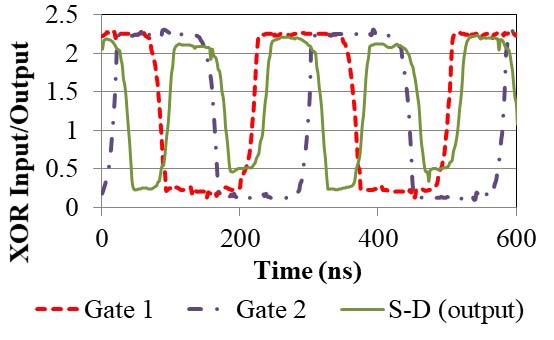
制造的异或开关。(b)制造的或门开关。桥结构宽18 μm，长30 μm。(c)异或门G1+ S和G2+ D器件的I–V特性。(d)输入信号及异或输出随时间的变化。(e)聚焦离子束加工的1‐μm镍开关。(f)异或开关在 0.1 V迟滞下的100秒I–V曲线。插图：由0.1 V迟滞引起的粘附力。)

图3(c) 显示了将G1连接到S、G2连接到D时异或器件的I–V特性。该器件的I–V特性在循环过程中略有变化，但可以明显看到区分导通状态与关断状态的电压范围。由于异或门具有较大的接触面积，其I–V滞后现象（ΔV ∼ 0.5 V）比纳米机电系统开关更大。图3(d) 显示了异或门的输出特性。当两个输入均为高电平或低电平时，器件关闭，其他情况下则导通。波形瞬态特性与桥结构的机械响应以及RC时间常数充电效应相关。物理模型将考虑这些瞬态特性，以及吸合电压、源漏接触电阻和由范德华力引起的可能滞后现象。实验测得的Vpull−in、滞后(ΔV)、粘附力、漏电流和开关速度随后与模型结果进行比较，并通过迭代调整模型参数获得了良好的一致性。

III. 使用纳米机电系统的数字设计

A. 基本门的设计

类似于上述讨论的异或门和或纳米机电系统器件，我们使用单个纳米机电系统器件结构设计了与门、与非门、反相器、同或门以及缓冲器等基本逻辑门。

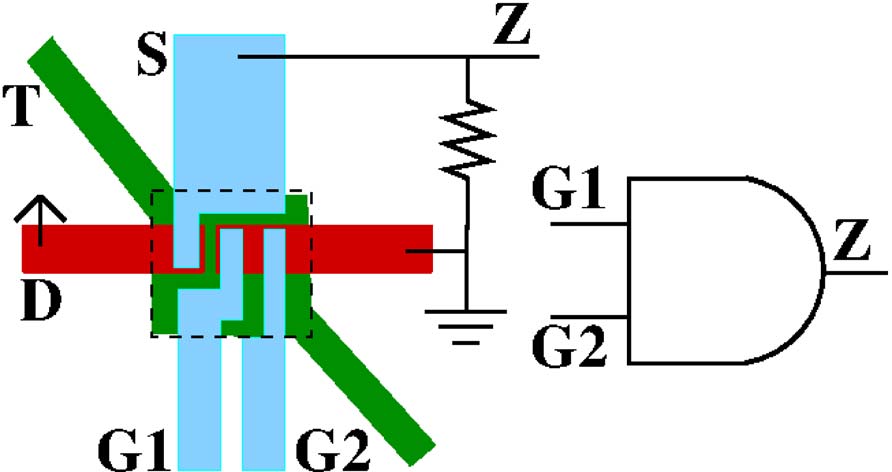
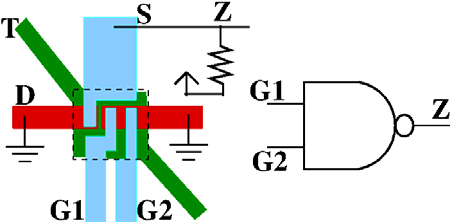
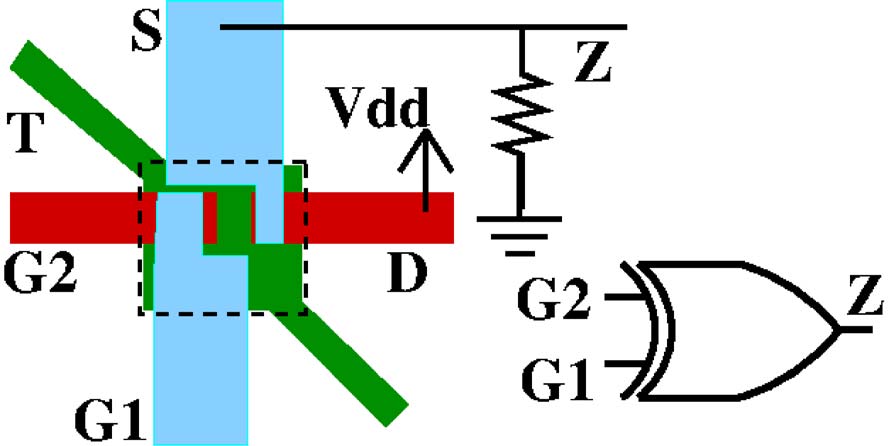
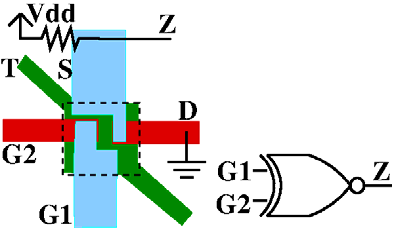
如图4(a)所示，一个与门由单个或纳米机电系统开关和一个电阻器构成。在图4(a)中，与门的漏极连接到V dd ，输出端Z为连接到源极（S）和下拉电阻至接地。在这种配置下，当 G1= G2= 1时，D和S导通，输出端连接至Vdd(Z= 1)。在所有其他情况下，G1、G2和接地之间的电势差不足以产生静电力来吸引两个桥结构。此时，D与S未导通，导致输出被下拉至接地（Z= 0）。该与门仅需一个纳米机电系统器件，而互补金属氧化物半导体中通过级联一个与非门和一个反相器需要六个独立开关：每个门节省了五个开关。这使得我们提出的与门速度快四倍，因为它只需一次机械运动即可计算输出Z。在复杂设计中，这将累积成显著的功耗和芯片面积节省。如图4(b)所示，使用单个纳米机电系统器件构建了一个异或门/同或门可通过如异或门开关和一个电阻器实现，如图4(c)和（d）所示。

或者，可将S接触端设计为在高电位处与顶部电极接触，以实现真正的互补操作。在当前配置中，其类似于传输门晶体管逻辑，关键区别在于此处使用单个器件并具有两个输入，而在传输门方法中，每个输入需要一个独立的开关。我们的“功能型”器件可以设计为具有多个输入。

纳米机电系统器件可以具有比硅基MOSFET更好的ION/IOFF性能。在“导通状态”下，微机电系统开关提供金属‐金属接触，接触电阻可低至约1 mΩ。在“关断状态”下，空气间隙提供 10^14 Ω。在文献报道的一些微机电系统器件中，采用钨作为电极材料。钨容易氧化，而氧化钨具有半导体特性，会引入较大的接触电阻，从而使“导通”电阻较高（∼kΩ）。金属‐金属微机电系统开关的亚阈值电流斜率已达到 1–10 mV/十倍频程。其阈值电压可低至100 mV，若阈值电压较高，可通过衬底偏置[11],[12]和弯曲元件的优化进行调节。

与门。 (b)与非门。 (c)异或门。 (d)同或门。)

B. 使用纳米机电系统的存储器设计

利用范德华力和卡西米尔力引起的粘附现象，可以实现具有无限锁存能力的纳米机电系统器件和开关。一旦这些器件被配置处于导通状态或关断状态时，它们可以在没有电子反馈机制的情况下无限期地保持该状态。因此，在互连设计中使用的已配置纳米机电系统开关可以支持持续传播，将正确的输入信号连接到正确的输出。这在可重构设计中非常有用，因为配置可以由开关本身保持，从而无需SRAM配置开关，降低功耗和芯片面积。图5展示了一种使用反相器和纳米机电系统开关构建的D型锁存器设计。如图5(a)所示，该 D型锁存器设计不需要反馈和传输门。反相器通过纳米机电系统开关的粘附来保持状态，类似于[13]和[14]中讨论的存储技术。在我们的技术中，可以通过在计算前对 T端子进行编程以释放桥接结构，从而将设计中的任何门变为存储单元。此外，也可以使用磁场实现存储，但纳米机电系统中使用的金属应具有铁磁性。还可以采用机械锁存机制。

这在可重构设计中非常有用，因为配置可以由开关保持，从而无需SRAM配置开关，降低了功耗和芯片面积。图5 展示了一种使用三个纳米机电系统开关构成的D型锁存器设计。

如图5(a)所示，该D型锁存器设计不需要反馈和传输门。在 图5(a)中，当时钟信号为高电平时，X1纳米机电系统开关将数据输入连接到X0和X1纳米机电系统开关的G2输入。如果数据输入为0（1），则X0开关处于关断状态（导通状态），而X2开关处于导通状态（关断状态）。此时，QB被设置为逻辑0（1）。当时钟信号为低电平时，XI开关被关断。由于粘附效应，X0和X11保持其原有状态。此时，QB保持时钟信号等于1时的状态。该电路的行为类似于D型锁存器。纳米机电系统开关的粘附状态类似于[13]和[14]中讨论的存储技术。

在我们的技术中，可以通过在计算前对T端子进行编程以释放桥接结构，从而将设计中的任何门变为存储单元。此外，也可以利用磁场实现存储功能，但纳米机电系统中使用的金属应具有铁磁性。另外，还可以采用机械锁存机制。

无反馈的纳米机电系统D型锁存器设计。b) 使用图1所示纳米机电系统 实现的D型锁存器。)

使用CMOS设计流程和综合工具[15]可以实现纳米机电系统逻辑功能器件和电路。所提出的纳米机电系统门包括具有反馈的与门、与非门、或门、或非门、异或门、同或门、缓冲器、非门和锁存器，而基于粘附的锁存器为设计人员提供了一套完整的基本单元，能够实现任意逻辑设计，并构建可供综合工具使用的标准单元库。在低功耗纳米机电系统中，设计人员在优化纳米机电系统设计时只需考虑开关活动和毛刺。

IV. 三维有限元分析物理纳米机电系统器件模型

我们构建了一个三维有限元物理器件模型，该模型捕捉了多物理场现象，并利用COMSOL多物理场有限元分析仿真工具再现了纳米机电系统开关的静态和动态行为。基于该三维有限元分析模型，我们计算了纳米机电系统参数，并通过已制造器件的测量结果验证了这些参数的准确性。

A. 吸合电压

为了对纳米机电系统开关的吸合电压进行建模，采用静态参数求解器通过扫描栅极电极上的施加电压来实现。静电力随间隙距离呈二次方增加，而恢复力则随间隙距离呈线性增加。当两个桥结构之间的间隙大于临界值时，恢复力始终大于静电力 ∼2/3g0[16]，其中g0为两个电极之间的初始间隙距离。当求解器找到能使桥结构达到临界间隙的最小电压（即吸合电压）时，便停止运行。仿真得到的吸合电压如图6所示。需要注意的是，当发生吸合时，间隙距离约为10 nm，并且我们在仿真中考虑了范德华吸引力的影响，如图6(b)所示。在图3(f)中，实验测得的Fs为1.5 nN，对应于漏源极间作用力。

在纳米机电系统开关中，I–V滞后通常由器件电极之间的粘附力（Fs）引起。众所周知，粘附力（范德华力和卡西米尔力）取决于表面形貌以及电极材料的电磁特性。在我们的器件中，我们探索了引入表面层（如硫化物和氧化物）、表面纳米结构化以及不同金属（Au和W）来降低粘附及其导致的滞后现象。一些研究人员还开发了聚合物涂层和衬底偏置技术，以调节阈值电压以及滞后[11]–[13]。栅极电极之间的范德华力比漏源极电极之间更大的主要原因是，栅极电极的面积更大，这是为了产生更大的电容从而降低吸合电压。

异或门 吸合电压。 (b)范德华力。)

B. 开关时间

我们通过在有限元分析中采用瑞利阻尼模型考虑粘滞阻尼来建模开关时间仿真工具。栅极电极之间的电势差设置为大于吸合电压的值。求解器在接触发生之前停止。所模拟的异或门 开关的开关时间如图7(a)所示。

需要指出的是，这些开关中的阻尼力非常小，因为间隙距离15纳米小于空气的平均自由程65纳米[14]。图 7(b)显示了栅极和漏源电极的电容随时间的变化。它们是通过对单位面积电容在重叠表面积分计算得到的。间隙距离会影响动电极到达并接触第二电极所需的运动时间，前提是动电极在其共振频率下被激发。如果不是，则施加电压的振幅变得更加重要。

C. 隧穿电流

由于间隙较小，必须考虑器件隧穿电流。隧穿电流通过在重叠的电极上对Fowler‐Nordheim隧穿电流密度方程进行积分来建模，如下所示:

$$
J= 1.5× 10^6 E^{-6} \phi e^{9.87/ \sqrt{\phi}} e^{-6.53×10^7 \sqrt{\phi}/E}
$$

其中 $E$ 是电极表面法向方向的电场（V/cm），$\phi$ 为功函数（钨的功函数为4.6电子伏特[19]），而$J$是隧穿电流密度（A/cm²）。如图8(a)所示，隧穿电流非常小，数量级为 10⁻²⁹到 10⁻²⁸。这些纳米机电系统器件几乎具有零漏电流，从而大幅降低静态功耗。

D. 接触面积

为了模拟开关的接触面积，我们使用了增广拉格朗日方法和参数化FEA仿真工具求解器。图8(b)显示了漏极与源极之间的接触面积随载荷力的变化关系。该接触面积用于计算纳米机电系统电极的接触电阻和电容。

隧穿电流和 (b)接触面积。（步骤为数值伪影。）)

V. 电路仿真

NEMS电路仿真模型的推导基于NEMS多物理场三维有限元物理器件COMSOL模型。该NEMS电路仿真模型能够获得与三维有限元分析模型相同的器件特性，但所需CPU时间更少且内存需求更低。这使得在电路仿真中可以对NEMS电路进行评估，从而实现混合NEMS和CMOS设计。为了建立该电路模型，我们首先使用COMSOL计算所有关键的器件参数，如弹簧常数、阻尼、接触电阻和电容。这些参数将在下文讨论，并被用于集总机械和电路模型中，以高效地仿真NEMS。

A. 电路仿真模型

纳米机电系统（NEMS）电路仿真模型由机械集总模型和下文讨论的电路模型组成。

B. 集总机械模型

图9中的机械集总模型采用改进的弹簧‐质量‐阻尼方程(2)来描述每个桥结构的运动，其中$x$是桥结构中点处的位移，$k_{eff}$是有效桥刚度常数，$m_{eff}$是有效桥质量，$c_d$是粘性阻尼系数，$k_d$是弹性阻尼系数，$F_{elec}$是静电力，而$F_{vdw}$是范德华力

$$
m_{eff} \ddot{x} + c_d \dot{x} + (k_{eff} + k_d)x = F_{elec} + F_{vdw}
\quad (2)
$$

$$
F_{elec} = \sum_i 0.5 \varepsilon_0 \frac{V^2 A_i}{\text{gap}_i^2}
\quad (3)
$$

$$
F_{vdw} = \sum_i \frac{H}{6\pi \text{gap}_i^3}
\quad (4)
$$

$$
k_{eff} = k_1 + k_2, \quad c_d = B_1 + B_2, \quad k_d = k_{d1} + k_{d2}.
\quad (5)
$$

为了解决（2），我们从三维有限元物理器件模型中提取机械参数。在每个时间步长，根据公式（3）和（4）计算载荷力（静电和范德华力），其中$V$为电势，$A$为面积，$\varepsilon_0$为真空介电常数，$H$为哈梅克常数（对于大多数材料为$(0.4–4)\times10^{-19}\,\text{J}$ [20]），$\text{gap}$为间隙距离。这是通过将每个桥结构沿其长度分割为$n$段来实现的。

栅极电极的重叠区域被划分为由上桥和下桥段正交交叉形成的方格。通过使用四阶龙格‐库塔法对(2)进行数值求解，计算每个时间步长中间桥的位移，然后利用几何关系计算每一段的位移。我们通过从初始间隙距离中减去相应上桥和下桥段的位移来计算每个重叠方格中两桥之间的间隙距离$\text{gap}_i$，以更新载荷力。

C. 系数推导

在本节中，我们介绍阻尼系数$c_d (=B_1+B_2)$、$k_d (=k_{d1}+k_{d2})$、有效刚度系数$k_{eff}(=k_1+k_2)$以及有效质量$m_{eff}$的确 定。

1) 阻尼系数：

阻尼是纳米机电系统结构动态行为中的主要阻尼成分，尤其是在低环境压力下[21],[22]。挤压膜阻尼包括黏性阻尼和电气阻尼。黏性阻尼通过在COMSOL多物理场中求解修正雷诺方程来实现，如下所示:

$$
\nabla_t\left(\frac{h_0^3}{Q_{oh}} \nabla_t p_f - 6\eta h_0(u_t + u_{0,t})\right) = 12\eta\left( \frac{dp_f}{dt} h + p \frac{dh}{dt} \right)
\quad (6)
$$

其中，$p_f$为膜压变化，$h = h_0 + \Delta h(t)$为空气间隙距离，由初始间隙和边界法向方向的变形组成，$\eta$表示常温下的流体黏度，$p = p_a + p_f$为总流体压力，由初始压力和压力变化组成，$u_t$和$u_{0,t}$分别为运动结构的切向速度和$Q_{ch} = 1 + 9.638K_s^{1.159}$为考虑稀薄气体效应的相对流量函数。我们开关中的电学阻尼通过以下方程计算得出:

$$
P_{electric} = p_a \frac{h}{\Delta \dot{h}}
\quad (7)
$$

阻尼力的仿真结果用于推导阻尼系数，其中粘性阻尼力与中间桥的速度成正比，弹性阻尼力与中间桥的位移成正比。

粘性。 (b) 电的。)

2) 有效刚度系数：

为了建模有效刚度系数，我们从三维有限元物理模型中提取每个桥结构的机械能。该有效刚度系数是通过计算得出的

$$
k_{eff} = \frac{2E_M}{x^2}
\quad (8)
$$

其中$E_M$为机械能，$k_{eff}$为有效刚度系数，$x$为位移。图11显示了计算得到的有效刚度系数随桥结构位移的变化情况。

3) 有效质量：

为了计算每个桥结构的有效质量，将三维有限元物理器件模型配置为求解共振频率，该频率对应于桥结构位移达到最大值时的频率。图12显示了异或开关的共振频率。据此，我们使用以下方程计算每个桥结构的有效质量。

$$
m_{eff} = \frac{k_{eff}}{(2\pi f)^2}
\quad (9)
$$

上桥。(b)下桥。)

D. 电路模型

电路模型能够在电路设计环境中模拟纳米机电系统开关，是电阻器和电容的互连。由于机械纳米机电系统开关在关断状态和导通状态下的电路模型不同。

在此推导中，每个可变电容器如图13所示，通过计算栅极电极重叠区域的间隙变化得到。因此，电容值等于栅极电极重叠区域上各段电容的总和。为了建模可变电阻器$R_{DS}$（如图13所示），需计算漏极与源极之间的漏电流。漏电流包含三个部分：隧穿电流、表面电流以及开关操作期间为电容充电所产生的开关电流。我们使用福勒‐诺德海姆隧穿电流来计算隧穿电流。表面漏电流依赖于工艺，并可通过表面处理降低，其值可通过实验测量结果的曲线拟合确定。开关期间为电容充电所产生的开关电流通过$(V\Delta C/\Delta t)$计算，其中$V$为电势差。可变电阻器由栅极电极重叠区域上每一段的漏电流的倒数和确定。为了建模导通状态下的电阻，接触面积由三维有限元物理器件模型计算得出。由于钨的电子平均自由程远小于接触面积的有效半径，接触电阻由扩散散射机制[19]决定，如下方程所示[24]，其中$\rho$为镍的电阻率，$r$为从接触面积拟合得到的圆形区域的半径。其余具有固定值的电阻器和电容器则通过简单电阻和电容方程进行建模。

$$
R = \frac{\rho}{2r} \quad \text{and} \quad C = \frac{\varepsilon_0 \cdot \text{Area}}{g}
\quad (10)
$$

异或门和(b)或门。开关导通状态模型： (c)异或门和(d)或门。)

E. 电路仿真的验证

为了验证静态和动态模式下的模型精度，我们使用推导出的电路仿真模型和三维有限元分析物理器件模型来获得器件的特性。表I显示了器件开关时间比较。

模型	开关时间 (ns)
三维有限元分析模型	8.2
电路仿真模型	8.0

表I 开关时间比较

图14显示了器件的间隙距离、静电力、范德华力以及由电路仿真和三维有限元分析模型得出的电容。这些推导出的器件参数与从三维有限元分析模型得出的结果非常接近。所推导出的电路仿真模型能够利用快速电路仿真技术，以与缓慢的三维有限元物理器件模型相同的精度，再现开关的机械和电气特性。

开关时间. (b)范德华. (c)静电. (d)电容.)

F. 纳米机电系统仿真

所推导的电路仿真模型在纳米机电系统电路仿真器中实现。该电路仿真器通过四阶龙格‐库塔方法对所推导的机械集总模型进行动态数值求解，并相应地更新校准后的电路模型（可变电气元件）。电路仿真器采用改进节点分析技术[25]以及迭代的牛顿‐拉夫森方法。所构建的电路仿真器能够准确评估任何纳米机电系统电路的功能、时序和功耗。图15(a)显示了具有输入{A、B和Cin}以及输出{Sum = A ⊕ B ⊕ Cin；Cout = A ∧ B + B ∧ Cin + A ∧ Cin}的1位加法器。由所开发的仿真器生成的该加法器的输入‐输出波形如图15(b)所示。

1位加法器设计和 (b)波形。 (c)基准电路规模和 (d)其平均功耗。)

VI. 仿真设置与结果

A. 基准电路评估

我们计算了使用纳米机电系统和互补金属氧化物半导体技术设计的ISCAS‐85基准电路的功耗。纳米机电系统的ISCAS‐85功耗通过开发的电路仿真器进行评估，而体互补金属氧化物半导体技术（45纳米和65纳米）则用于通过ELDO仿真器计算互补金属氧化物半导体基准电路的功耗。在评估过程中使用了45纳米[26]和65纳米[27]的PTM模型。图15(c)和(d)展示了纳米机电系统和互补金属氧化物半导体技术在活动模式下的尺寸和平均功耗[5]。

仿真结果表明，纳米机电系统电路具有显著的节能效果。功耗的大幅降低可归因于纳米机电系统设计所需的开关数量更少，以及纳米机电系统设计在关断状态下的漏电几乎为零。较大节点的互补金属氧化物半导体的漏电功耗低于45纳米节点，但仍高于纳米机电系统。

VII. 结论

本文中，我们提出了两种新型纳米机电系统开关设计，其具有几乎为零的漏电流、低工作电压、低开关时间、非常大的导通电流、可重复的开关特性、超低功耗以及小占板面积。这些开关可利用CMOS制造工艺进行制造，从而实现混合纳米机电系统‐CMOS设计。我们提出了一个三维有限元物理器件模型以及一个更简单的电路仿真模型。我们展示了纳米机电系统技术相较于CMOS在功耗降低方面有3到4倍的提升。本文最重要的贡献在于将吸合/释放电压等电学实验参数与粘附力、刚度以及其他来自独立测量的参数相关联。