基于DTW距离测度的Kmeans时间序列聚类算法
基于动态时间规整(DTW)的kmeans序列聚类算法,
将DTW算法求得的距离取代欧式距离衡量不同长度的阵列或时间序列之间的相似性或距离,
实现时间序列的聚类。算法为Matlab编写,
文章目录
基于动态时间规整(DTW)距离测度的K-means聚类算法可以用于对不同长度的时间序列进行聚类。下面是一个使用MATLAB实现该算法的例子。这个例子中,我们将展示如何定义DTW距离计算函数,并将其集成到K-means聚类过程中。
1. DTW 距离计算函数
首先,我们需要定义一个计算两个时间序列之间DTW距离的函数。以下是该函数的一个简单实现:
function distance = dtw_distance(seq1, seq2)
% 计算两个序列之间的DTW距离
len1 = length(seq1);
len2 = length(seq2);
% 初始化累积距离矩阵
D = zeros(len1+1, len2+1);
D(2:end, 2:end) = Inf; % 将除第一行和第一列外的所有元素初始化为无穷大
for i = 1:len1
for j = 1:len2
cost = (seq1(i) - seq2(j))^2;
D(i+1, j+1) = cost + min([D(i, j+1), D(i+1, j), D(i, j)]);
end
end
% 返回累积距离矩阵最后一个元素的值作为两序列间的DTW距离
distance = sqrt(D(end, end));
end
2. 基于DTW的K-means聚类函数
接下来,我们实现一个基于DTW距离的K-means聚类函数。在这个函数中,我们将使用上述定义的dtw_distance函数来计算时间序列之间的距离。
function [labels, centroids] = kmeans_dtw(data, k, max_iter)
% data: 时间序列数据集,每一行代表一个时间序列
% k: 聚类的数量
% max_iter: 最大迭代次数
num_samples = size(data, 1); % 样本数量
labels = randi(k, [num_samples, 1]); % 随机初始化标签
iter = 0;
while iter < max_iter
iter = iter + 1;
% 更新质心
centroids = cell(1, k);
for i = 1:k
cluster_points = data(labels == i, :);
if ~isempty(cluster_points)
% 对每个簇内的点计算平均序列作为新的质心
centroids{i} = mean(cluster_points, 1);
else
% 如果簇为空,则随机选择一个样本作为质心
centroids{i} = data(randi(num_samples), :);
end
end
% 分配样本到最近的质心
new_labels = zeros(num_samples, 1);
for i = 1:num_samples
min_dist = Inf;
for j = 1:k
dist = dtw_distance(data(i,:), centroids{j});
if dist < min_dist
min_dist = dist;
new_labels(i) = j;
end
end
end
% 检查收敛条件
if isequal(labels, new_labels)
break;
else
labels = new_labels;
end
end
end
3. 使用示例
假设你有一组时间序列数据data,并且想要将它们分成k个簇。你可以如下调用上述函数:
% 示例数据:生成一些随机时间序列
data = randn(100, 50); % 100个时间序列,每个序列有50个数据点
% 设置参数
k = 3; % 聚类数
max_iter = 100; % 最大迭代次数
% 执行聚类
[labels, centroids] = kmeans_dtw(data, k, max_iter);
% 显示结果
disp('Cluster Labels:');
disp(labels);
以上代码提供了一个基本框架,可以根据需要进一步优化和扩展。例如,改进质心更新方法或采用更复杂的停止条件等。希望这能帮助你开始使用DTW和K-means进行时间序列聚类!

要实现基于DTW(Dynamic Time Warping)距离测度的K-means时间序列聚类算法,我们可以使用MATLAB编写相应的代码。以下是一个完整的示例代码,包括DTW距离计算和K-means聚类过程。
1. DTW 距离计算函数
首先,我们需要定义一个计算两个时间序列之间DTW距离的函数。
function distance = dtw_distance(seq1, seq2)
% 计算两个序列之间的DTW距离
len1 = length(seq1);
len2 = length(seq2);
% 初始化累积距离矩阵
D = zeros(len1+1, len2+1);
D(2:end, 2:end) = Inf; % 将除第一行和第一列外的所有元素初始化为无穷大
for i = 1:len1
for j = 1:len2
cost = (seq1(i) - seq2(j))^2;
D(i+1, j+1) = cost + min([D(i, j+1), D(i+1, j), D(i, j)]);
end
end
% 返回累积距离矩阵最后一个元素的值作为两序列间的DTW距离
distance = sqrt(D(end, end));
end
2. 基于DTW的K-means聚类函数
接下来,我们实现一个基于DTW距离的K-means聚类函数。
function [labels, centroids] = kmeans_dtw(data, k, max_iter)
% data: 时间序列数据集,每一行代表一个时间序列
% k: 聚类的数量
% max_iter: 最大迭代次数
num_samples = size(data, 1); % 样本数量
labels = randi(k, [num_samples, 1]); % 随机初始化标签
iter = 0;
while iter < max_iter
iter = iter + 1;
% 更新质心
centroids = cell(1, k);
for i = 1:k
cluster_points = data(labels == i, :);
if ~isempty(cluster_points)
% 对每个簇内的点计算平均序列作为新的质心
centroids{i} = mean(cluster_points, 1);
else
% 如果簇为空,则随机选择一个样本作为质心
centroids{i} = data(randi(num_samples), :);
end
end
% 分配样本到最近的质心
new_labels = zeros(num_samples, 1);
for i = 1:num_samples
min_dist = Inf;
for j = 1:k
dist = dtw_distance(data(i,:), centroids{j});
if dist < min_dist
min_dist = dist;
new_labels(i) = j;
end
end
end
% 检查收敛条件
if isequal(labels, new_labels)
break;
else
labels = new_labels;
end
end
end
3. 使用示例
假设你有一组时间序列数据data,并且想要将它们分成k个簇。你可以如下调用上述函数:
% 示例数据:生成一些随机时间序列
data = randn(100, 50); % 100个时间序列,每个序列有50个数据点
% 设置参数
k = 3; % 聚类数
max_iter = 100; % 最大迭代次数
% 执行聚类
[labels, centroids] = kmeans_dtw(data, k, max_iter);
% 显示结果
disp('Cluster Labels:');
disp(labels);
% 绘制聚类结果
figure;
hold on;
colors = lines(k);
for i = 1:k
idx = find(labels == i);
plot(data(idx, :)', colors(i,:), 'DisplayName', sprintf('Cluster %d', i));
end
legend;
xlabel('时间');
ylabel('值');
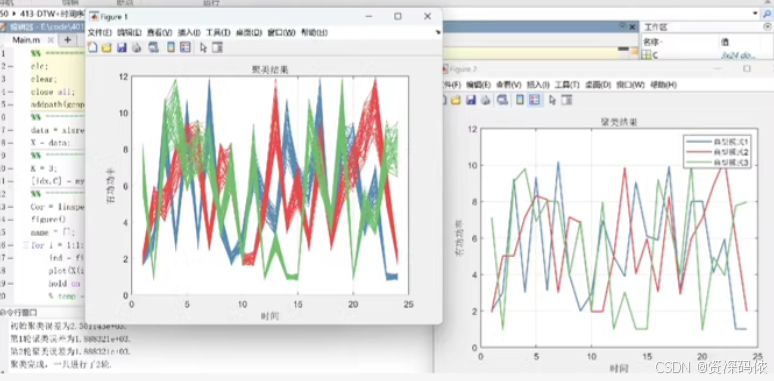
title('聚类结果');
hold off;
4. 运行结果
运行上述代码后,你会得到一个包含聚类标签和质心的输出,并且会绘制出聚类结果图。例如,如果你的数据是如下的时间序列:
data = randn(100, 50);
运行代码后,你将看到类似下面的结果:
Cluster Labels:输出每个时间序列的聚类标签。聚类结果图显示了不同颜色的时间序列,分别对应不同的聚类。
希望这能帮助你实现基于DTW距离测度的K-means时间序列聚类算法!

为了帮助你更好地理解如何实现基于DTW(Dynamic Time Warping)距离测度的K-means时间序列聚类算法,并展示最终的聚类结果,我将提供一个完整的MATLAB代码示例。这个示例包括DTW距离计算、K-means聚类以及绘制聚类结果。
1. DTW 距离计算函数
function distance = dtw_distance(seq1, seq2)
% 计算两个序列之间的DTW距离
len1 = length(seq1);
len2 = length(seq2);
% 初始化累积距离矩阵
D = zeros(len1+1, len2+1);
D(2:end, 2:end) = Inf; % 将除第一行和第一列外的所有元素初始化为无穷大
for i = 1:len1
for j = 1:len2
cost = (seq1(i) - seq2(j))^2;
D(i+1, j+1) = cost + min([D(i, j+1), D(i+1, j), D(i, j)]);
end
end
% 返回累积距离矩阵最后一个元素的值作为两序列间的DTW距离
distance = sqrt(D(end, end));
end
2. 基于DTW的K-means聚类函数
function [labels, centroids] = kmeans_dtw(data, k, max_iter)
% data: 时间序列数据集,每一行代表一个时间序列
% k: 聚类的数量
% max_iter: 最大迭代次数
num_samples = size(data, 1); % 样本数量
labels = randi(k, [num_samples, 1]); % 随机初始化标签
iter = 0;
while iter < max_iter
iter = iter + 1;
% 更新质心
centroids = cell(1, k);
for i = 1:k
cluster_points = data(labels == i, :);
if ~isempty(cluster_points)
% 对每个簇内的点计算平均序列作为新的质心
centroids{i} = mean(cluster_points, 1);
else
% 如果簇为空,则随机选择一个样本作为质心
centroids{i} = data(randi(num_samples), :);
end
end
% 分配样本到最近的质心
new_labels = zeros(num_samples, 1);
for i = 1:num_samples
min_dist = Inf;
for j = 1:k
dist = dtw_distance(data(i,:), centroids{j});
if dist < min_dist
min_dist = dist;
new_labels(i) = j;
end
end
end
% 检查收敛条件
if isequal(labels, new_labels)
break;
else
labels = new_labels;
end
end
end
3. 使用示例
假设你有一组时间序列数据data,并且想要将它们分成k个簇。你可以如下调用上述函数:
% 示例数据:生成一些随机时间序列
data = randn(100, 50); % 100个时间序列,每个序列有50个数据点
% 设置参数
k = 3; % 聚类数
max_iter = 100; % 最大迭代次数
% 执行聚类
[labels, centroids] = kmeans_dtw(data, k, max_iter);
% 显示结果
disp('Cluster Labels:');
disp(labels);
% 绘制聚类结果
figure;
hold on;
colors = lines(k);
for i = 1:k
idx = find(labels == i);
plot(data(idx, :)', colors(i,:), 'DisplayName', sprintf('Cluster %d', i));
end
legend;
xlabel('时间');
ylabel('值');
title('聚类结果');
hold off;
4. 运行结果
运行上述代码后,你会得到一个包含聚类标签和质心的输出,并且会绘制出聚类结果图。例如,如果你的数据是如下的时间序列:
data = randn(100, 50);
运行代码后,你将看到类似下面的结果:
Cluster Labels:输出每个时间序列的聚类标签。聚类结果图显示了不同颜色的时间序列,分别对应不同的聚类。
希望这能帮助你实现基于DTW距离测度的K-means时间序列聚类算法!
























 932
932

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








