2023第十三届MathorCup高校数学建模挑战赛C题解析_2023mathorcup数学建模挑战赛答案

原创

于 2025-01-20 08:44:46 发布 · 2.1k 阅读

48 ·

CC 4.0 BY-SA版权

文章标签：

#数学建模 #c语言 #开发语言

2023第十三届MathorCup高校数学建模挑战赛C题解析

题目
解析
- 前言

题目

C 题电商物流网络包裹应急调运与结构优化问题
电商物流网络由物流场地（接货仓、分拣中心、营业部等）和物流场地之间的运输线路组成，如图 1 所示。受节假日和“双十一”、“618”等促销活动的影响，电商用户的下单量会发生显著波动，而疫情、地震等突发事件导致物流场地临时或永久停用时，其处理的包裹将会紧急分流到其他物流场地，这些因素均会影响到各条线路运输的包裹数量，以及各个物流场地处理的包裹数量。
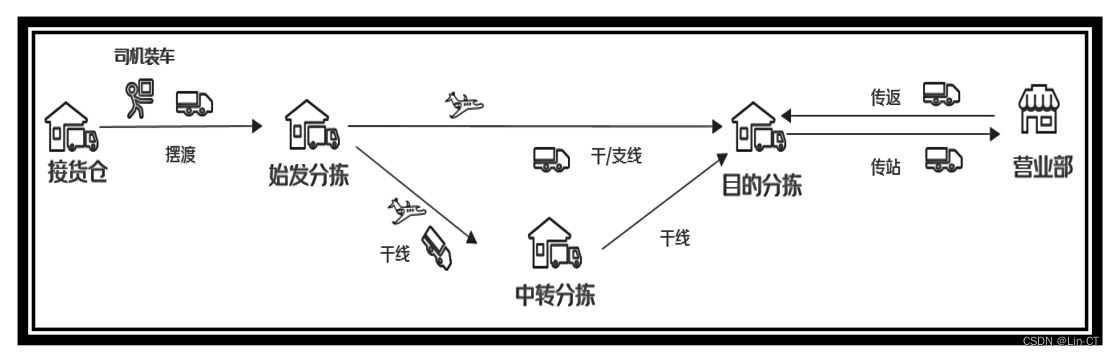
在这里插入图片描述

图 1 电商物流网络示意图
如果能预测各物流场地及线路的包裹数量（以下简称货量），管理者将可以提前安排运输、分拣等计划，从而降低运营成本，提高运营效率。特别地，在某些场地临时或永久停用时，基于预测结果和各个物流场地的处理能力及线路的运输能力，设计物流网络调整方案，将会大大降低物流场地停用对物流网络的影响，保障物流网络的正常运行。附件 1 给出了某物流网络在 2021-01-01 至 2022-12-31 期间每天不同物流场地之间流转的货量数据，该物流网络有 81 个物流场地，1049 条线路。其中线路是有方向的，比如线路 DC1→DC2 和线路 DC2→D

最低0.47元/天解锁文章

确定要放弃本次机会？

福利倒计时

: :

立减 ¥

普通VIP年卡可用

立即使用

2501_90245708

关注关注

28
点赞
踩
48

收藏

觉得还不错? 一键收藏
0
评论
分享

复制链接

分享到 QQ

分享到新浪微博

扫一扫
举报

举报

2023 高教社杯 数学建模国赛（B题）深度超全剖析|数学建模完整代码+建模过程全解全析

2301_79650538的博客

09-08

1万+

当大家面临着复杂的数学建模问题时，你是否曾经感到茫然无措？作为2021年美国大学生数学建模比赛的O奖得主，我为大家提供了一套优秀的解题思路，让你轻松应对各种难题。更新！！！让我们来看看B题！

2023 高教社杯 数学建模国赛（A题）深度剖析|Matlab+python代码双份提供|定日镜场的优化设计|数学建模完整代码+建模过程全解全析

2301_79650538的博客

09-08

4556

更新！当大家面临着复杂的数学建模问题时，你是否曾经感到茫然无措？作为2021年美国大学生数学建模比赛的O奖得主，我为大家提供了一套优秀的解题思路，让你轻松应对各种难题。希望这些想法对大家的做题有一定的启发和借鉴意义。构建以新能源为主体的新型电力系统，是我国实现“碳达峰”“碳中和”目标的一项重要措施。塔式太阳能光热发电是一种低碳环保的新型清洁能源技术[1]。

参与评论您还未登录，请先登录后发表或查看评论

2024全国研究生数学建模竞赛（数学建模研赛）ABCDEF题深度建模+全解全析+完整文章

Yilu264的博客

09-20

9549

2024全国研究生数学建模竞赛（数学建模研赛）ABCDEF题深度建模+全解全析+完整文章

2023第十三届MathorCup高校数学建模挑战赛C题解析

热门推荐

qq_43605229的博客

04-13

1万+

数学建模主要是让大家构建自己的模型，只要能解决问题的模型就是好模型，无标准答案。我个人的分析过程大致如下文，仅个人观点不一定是正确的，不说太多怕限制了大家的思维哈哈哈。

【2023 年第十三届 MathorCup 高校数学建模挑战赛】D 题航空安全风险分析和飞行技术评估问题 27页论文及代码_2023mathorcupd题优秀论文

m0_60607245的博客

04-06

1043

Android移动开发、AIGC大模型、C C#、Go语言、Java、Linux运维、云计算、MySQL、PMP、网络安全、Python爬虫、UE5、UI设计、Unity3D、Web前端开发、产品经理、车载开发、大数据、鸿蒙、计算机网络、嵌入式物联网、软件测试、数据结构与算法、音视频开发、Flutter、IOS开发、PHP开发、.NET、安卓逆向、云计算**对于超限事件的研究，一般是通过规定飞行参数的集中区域设置超限阈值，将超出阈值部分的飞行记录找出来，进行重点分析，防范潜在隐患造成严重飞行事故。

2024第十三届MathorCup高校数学建模挑战赛C题解析_2024mathorcup数学建模挑战赛答案

2401_84182936的博客

05-03

1418

2022年MathorCup高校数学建模挑战赛D题1

08-03

2022年MathorCup高校数学建模挑战赛D题1 本题目是2022年MathorCup高校数学建模挑战赛D题1，主要涉及到移动通信网络站址规划和区域聚类问题。该题目可以分为三个子问题，分别是站址规划、扇区角度优化和区域聚类。 ...

2019年MathorCup高校数学建模挑战赛C题1

08-03

本资源的标题是"2019年MathorCup高校数学建模挑战赛C题1”，该标题表明这是一个数学建模挑战赛的题目，具体来说是2019年的MathorCup高校数学建模挑战赛的C题1。根据描述，这个题目是关于数学建模挑战赛的，题目...

2020年MathorCup高校数学建模挑战赛C题1

08-03

1. **数学建模**：本题是一个典型的数学建模问题，涉及到路径规划、最优化问题以及效率分析。数学建模是利用数学工具解决实际问题的过程，这里需要构建模型来优化拣货员的行走路线和任务分配，以提高仓库工作效率。 ...

2023年MathorCup数模C题赛题

qq_33690821的博客

04-13

2582

因此，大家放手去做即可。：如果物流场地 DC5 于 2023-01-01 开始关停，请在问题 1 的预测基础上，建立数学模型，将 DC5 相关线路的货量分配到其他线路使所有包裹尽可能正常流转，并使得 DC5 关停前后货量发生变化的线路尽可能少，且保持各条线路的工作负荷尽可能均衡。：在问题 2 中，如果被关停的物流场地为 DC9，同时允许对物流网络结构进行动态调整(每日均可调整)，调整措施为关闭或新开线路，不包含新增物流场地，假设新开线路的运输能力的上限为已有线路运输能力的最大值。

【2023 年第十三届 MathorCup 高校数学建模挑战赛】D 题航空安全风险分析和飞行技术评估问题 27页论文及代码

BetterBench的博客

05-02

5290

基于神经网络模型的飞行安全数据仿真模拟摘要飞行安全是民航运输业赖以生存和发展的基础。随着我国民航业的快速发展，针对飞行安全问题的研究显得越来越重要。本文首先参考附件数据并查阅大量资料飞行安全相关的数据进行相关分析处理，建立了基于飞行数据的主成分分析模型、梯度提升决策树（GBDT）模型和 BP-神经网络模型，最终实现航空安全风险分析以及对飞行技术评估。针对问题一，我们对附件中所给的数据进行了预处理，对缺失值和异常值进行处理，来减少错误数据对研究分析带来的影响。

【2023 年第十三届 MathorCup 高校数学建模挑战赛】 B 题城市轨道交通列车时刻表优化问题详细建模方案及代码实现

BetterBench的博客

04-13

7255

列车时刻表优化问题是轨道交通领域行车组织方式的经典问题之一。列车时刻表规定了列车在每个车站的到达和出发（或通过）时刻，其在实际运用过程中，通常用列车运行图来表示。图 1 为某一运行图的示例，图中每一条线表示一趟列车，横轴表示车站，纵轴表示时间，每一条线反映了一趟列车在不同时刻所处的相对位置，也称为运行线。比如，图中红色运行线表示，列车于 9：02 分从 D 站出发，于 9：05 分到达 C 站，停留 1 分钟后出发，于 9：09 分到达 B 站，停留 1 分钟后出发，于 10：03 分到达A 站。

2023年第十三届MathorCup高校数学建模挑战赛｜A题｜量子计算机在信用评分卡组合优化中的应用

m0_57656758的博客

04-13

5792

QUBO 模型是指二次无约束二值优化（Quadratic Unconstrained Binary Optimization）模型，它是一种用于解决组合优化问题的数学模型。在QUBO模型中，需要将问题转化为一个决策变量为二值变量，目标函数是一个二次函数形式优化模型。QUBO 模型可以运行在量子计算机硬件上，通过量子计算机进行毫秒级的加速求解。这种模型和加速方式在未来各行业中将得到广泛的实际应用。因此现阶段研究基于 QUBO 模型的量子专用算法十分有应用价值。例如。

【2023年Mathorcup杯数学建模竞赛C题】电商物流网络包裹应急调运与结构优化--完整作品分享

maligebilaowang的博客

05-08

5795

为了应对电商物流网络中物流场地和线路电商物流网络中物流场地和线路上货量波动的情况，设计合理的物流网络调整方案以保障物流网络的正常运行。本文运用 0-1 整数规划模型，多目标动态规划模型，给出了问题的结果。针对问题一,本文对附件 1 中所给的数据进行了预处理,排除了因疫情而导致的电商快递行业的异常数据并进行了归一化处理,得到 450 组有效数据。

2023 年第十三届“MathorCup” C 题包裹应急调运问题（解题思路）

KeepLearner——终生学习者的家园

04-13

2273

特别是当某些场地暂时或永久停用时，基于预测结果和每个物流场地的处理能力以及线路的运输能力，调整物流网络的设计方案将大大降低物流场地停用对物流网络的影响，确保物流网络的正常运作。在动态调整物流网络结构的前提下，将 DC9 场地相关线路的货物量分配给其他线路，使得各个线路的负载尽可能平衡，并尽量减少运输量变化的线路数。建立数学模型，在保证尽量少的影响和最小化未正常流转的货物累计总数的前提下，将 DC5 的货物量分配给其他线路，使得各个线路的负载尽可能平衡，并尽量减少运输量变化的线路数。

2023年全国大学生数学建模竞赛C题——针对蔬菜类商品定价与补货决策的研究

absths的博客

10-03

8778

2023年全国大学生数学建模竞赛C题——针对蔬菜类商品定价与补货决策的研究。本文针对生鲜超市中蔬菜类商品的补货和定价策略问题，建立时间序列预测模型，以及目标规划分析，从而让生鲜超市的收益达到最大。针对问题一，首先对数据进行处理，对销售量异常值进行剔除、对缺失值补0 处理，接着再基于附件1 与附件2 中的数据，将数据进行汇总整合，计算出每个品类以及每个单品的三年、每月和每天的总销售量，绘制柱状图，分析得到花叶类销售量最大；芜湖青椒( 这种单品的销量最大；

2023年MathorCup高校数学建模挑战赛大数据挑战赛赛题浅析

qq_33690821的博客

10-28

1677

对于问题一而言，即需要我们根据附件一-附件四的数据对各商家在各仓库的商品2023-05-16 至 2023-05-30 的需求量进行预测。并进行相似度分析，这里的相似度简单来讲，我认为可以使用相关性分析里面的最简单的person进行分析即可。选择相似度高的指标，作为问题二预测模型的指标进行预测即可。比赛时长为期7天的妈杯大数据挑战赛如期开赛，为了帮助大家更好的选题，首先给大家带来赛题浅析，为了方便大家更好的选题。问题三，即需要我们引入去年双十一期间的需求量数据进行分析关联性等，建立对应的预测模型即可。

2023年MathorCup高校数学建模挑战赛-大数据赛

qq_52590045的博客

10-23

537

最后各商家在各仓库的数据导入训练好的模型当中进行预测，输出预测出各商家在各仓库的商品2023-05-16至2023-05-30的需求量，并将其存放在相应的表格附件当中。再者将GDM聚类结果作为自变量，出货量作为因因变量，为了更好的迭代时间与空间维度的数据，构建基于模糊神经网络出货量预测模型（GD-FNN模型）对不同商家在不同仓库的商品出货量进行预测。最后将相关数据到训练好的模型当中，输出2023-05-16至2023-05-30的预测值存放到表1相应的位置，并对预测的准确度进行评价。

2023第十三届MathorCup高校数学建模挑战赛C题代码

最新发布

02-26

### 2023年第十三届MathorCup高校数学建模挑战赛C题代码实现针对电商物流网络中的包裹应急调运与结构优化问题，解决方案主要集中在如何通过合理的算法来提高配送效率并应对突发情况。以下是基于该竞赛的具体编程实现方法。 #### 数据预处理为了更好地模拟实际场景，在编写程序之前需先准备好数据集。这通常涉及读取输入文件、清洗异常值以及转换成适合计算的形式： ```python import pandas as pd def preprocess_data(file_path): """加载并清理原始数据""" df = pd.read_csv(file_path) # 清洗缺失值和其他不合理的数据点 df.dropna(inplace=True) return df ``` #### 构建图模型表示物流网络利用加权有向图可以有效地表达各个仓库之间的连接关系及其运输成本。这里采用邻接矩阵存储方式，并定义了一些辅助函数用于初始化和更新路径权重。 ```python from collections import defaultdict class Graph: def __init__(self, num_nodes): self.graph = [[float('inf')]*num_nodes for _ in range(num_nodes)] def add_edge(self, u, v, weight=1): self.graph[u][v] = min(weight, self.graph[u][v]) def get_neighbors(self, node_id): neighbors = [] for i in range(len(self.graph)): if self.graph[node_id][i] != float('inf'): neighbors.append((i, self.graph[node_id][i])) return neighbors ``` #### 应急调度策略设计——最短路优先分配法当发生紧急事件时，应迅速调整现有资源以满足新需求。此部分实现了Dijkstra算法求解单源最短路径问题，从而指导货物从最近可用节点发出。 ```python import heapq def dijkstra(graph, start_node): n = len(graph.graph) dist_to = [float('Inf')] * n visited = set() pq = [(0, start_node)] while pq: (dist, current_vertex) = heapq.heappop(pq) if current_vertex not in visited: visited.add(current_vertex) dist_to[current_vertex] = dist for neighbor, distance in graph.get_neighbors(current_vertex): old_dist = dist_to[neighbor] new_dist = dist + distance if new_dist < old_dist and neighbor not in visited: heapq.heappush(pq, (new_dist, neighbor)) return dist_to ``` #### 结构优化建议——遗传算法探索最优布局长期来看，改善整个系统的架构有助于降低运营成本并增强抗风险能力。下面给出了简单版GA框架来进行全局寻优操作。 ```python import random def genetic_algorithm(population_size, mutation_rate, crossover_rate, generations): population = initialize_population(population_size) best_fitness = None for generation in range(generations): fitness_scores = evaluate_fitness(population) mating_pool = select_mating_pool(fitness_scores) offspring = breed(mating_pool, crossover_rate) mutate(offspring, mutation_rate) next_generation = replace_worst_with_best(population, offspring, fitness_scores) population = next_generation max_fit = max(fitness_scores.values()) if best_fitness is None or max_fit > best_fitness: best_fitness = max_fit return find_chromosome_with_max_fitness(population), best_fitness ``` 上述代码片段展示了完整的流程，包括但不限于数据准备、图论基础建设、即时响应机制以及长远规划措施[^1]。