AR模型时序预测——预测未来（含完整代码）

一、前言

随着数据科学的快速发展，利用自回归（AR）模型进行时序预测已成为一个热门话题。AR模型因其简洁有效，广泛应用于各类预测任务。本文将介绍一套基于Matlab的AR模型时序预测代码，重点在于如何通过历史数据预测未来趋势。本文中的代码是完整可用的，读者只需复制到Matlab中即可运行。

AR时间预测完整代码

二、代码部分

代码分为以下几个部分：初始化、数据读取、数据预处理、模型拟合、预测以及作图。

1. 初始化

%% 1.初始化

 

clear

close all

clc

 

2. 数据读取

需要修改以下部分：

 

1.数据范围，例如A1:A16表示16年的数据。

 

%% 2.数据读取

 

data0 = xlsread('数据.xlsx', 'Sheet1', 'A1:A16');

data = data0(:, 1); % 获取数据列

 

3. 数据预处理

进行必要的数据预处理，以确保数据适用于AR模型。

%% 3.数据预处理

 

% 将数据转化为列向量

data = data(:);

N = length(data); % 数据长度

 

% 设置延迟阶数

p = 4; % 选择自回归阶数为4

 

4. 模型拟合

使用最小二乘法拟合AR模型。

%% 4.模型拟合

 

% 创建输入矩阵和输出向量

X = zeros(N - p, p);

y = zeros(N - p, 1);

 

for i = 1:N - p

    X(i, :) = data(i:i+p-1)'; % 自回归输入

    y(i) = data(i + p); % 目标输出

end

 

% 进行最小二乘法估计

theta = (X' * X) \ (X' * y); % 权重估计

 

5. 预测

在此部分，设置未来数据的预测。

%% 5.预测

 

forecastSteps = 4; % 预测未来4个步骤

predictions = zeros(forecastSteps, 1);

 

% 使用最后的p个数据进行预测

inputData = data(end-p+1:end);

 

for i = 1:forecastSteps

    prediction = theta' * inputData; % 预测值

    predictions(i) = prediction;

 

    % 更新输入数据

    inputData = [inputData(2:end); prediction]; % 更新输入

end

 

6. 作图

最后，对预测结果进行可视化。

%% 6.作图

 

figure

plot(1:N, data, 'k-o', 'linewidth', 1.5); % 真实值

hold on

plot(N+1:N+forecastSteps, predictions, 'b--h', 'linewidth', 1.5); % 预测值

legend('真实值', '预测值');

xlabel('时间序列'), ylabel('指标值');

title('AR模型预测');

set(gca, 'fontsize', 12);

 

三、结果展示

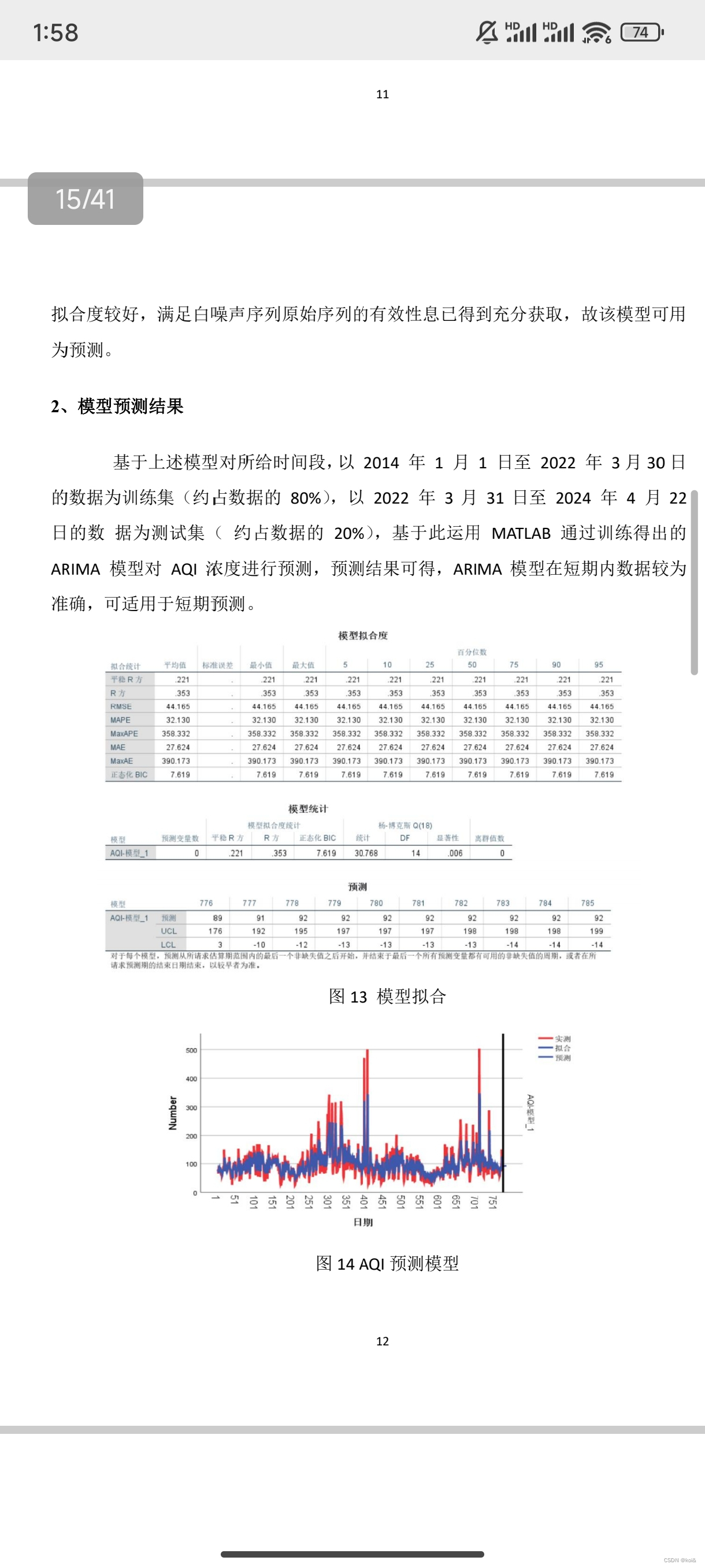
本文展示了AR模型在时序预测中的应用，提供了完整的Matlab代码。结果图表展示了真实值与预测值的对比。

 

四、结语

本文介绍了一种简单的自回归（AR）模型时序预测方法，并提供了完整的Matlab代码。尽管该方法在某些情况下可能会受到数据特性的影响，但它为初学者提供了良好的学习基础。未来可以考虑使用更复杂的模型（如ARIMA或SARIMA）来提高预测精度。希望这篇文章能够帮助你更好地理解AR模型在时序预测中的应用。