二分法方程求根（matlab代码）

       用二分法求方程f(x)=0的实根x*的近似值，其主要思想是:将含有根x*的隔根区间二分，通过判断二分点与边界点函数值的符号，逐步对半缩小隔根区间，直到缩小到满足精度要求，然后取最后二分区间的中点为根x的近似值。算法流程如下图所示:

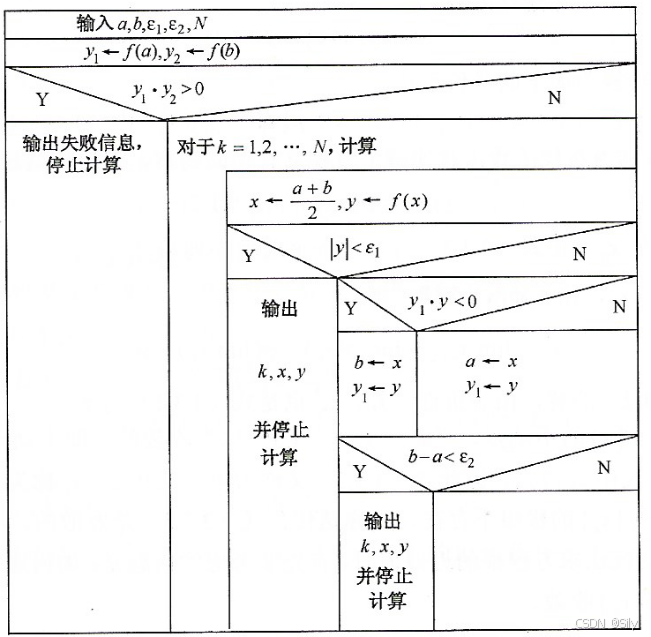
需要注意的是，二分法在使用之前首先要确定[a,b]区间为隔根区间。

举个例子：在区间[0,1]内用二分法求方程的近似根，要求误差不超过0.5*10^(-3)。

syms x % 定义变量
f = @(x) exp(x) + 10*x -2; % 求解方程
a = 0; b = 1; % 初始的区间上下限
n = 0; % 迭代次数
w = 0.5*power(10, -3); % 误差要求

while f(a) * f(b) < 0 % 存在根
x_0 = (a+b)/2 % 计算中点，开始二分
if f(x_0) == 0 % 零点即中点
break;
end
if f(a) * f(x_0) < 0 % 零点在左边的区间
b = x_0;
else % 零点在右边的区间
a = x_0;
end
n = n+1

if abs(a - b) < w % 判断是否满足精度条件
x_0 % 最终得到的近似解
n = n+1 % 迭代总次数
break;
end
end