物理信息神经网络杀疯了！Nature+Science=PINN

2024深度学习发论文&模型涨点之——PINN

物理信息神经网络（Physics-Informed Neural Networks，简称PINN）是一种结合了深度学习和物理学知识的机器学习模型。与传统的数据驱动的神经网络不同，PINN在学习过程中利用物理法则对模型进行指导，从而提高模型泛化能力，特别是在数据较少或噪声较大的情况下。

实际上，物理信息机器学习一直是火爆且好发论文的方向，目前已有多篇成果登上Nature及Science正刊。提起它的典型代表PINN，大家应该都不陌生。它通过将物理知识整合到机器学习模型中，能够克服传统方法对大量标记数据数据的依赖，在提高模型预测准确性、可解释性、数据利用效率方面，举足轻重！此外，该方向发展还不久，既有很多成果可参考，又有很多创新机会！你结合自己的数据集，换个场景，便又是新文章！

小编整理了一些PINN【论文+代码】合集，需要的同学关注公人人人号“AI创新工场”回复“PINN”即可全部领取

论文精选

论文1：

【Nature】Physics-informed learning of governing equations from scarce data

从稀缺数据中学习物理信息以掌握控制方程

方法

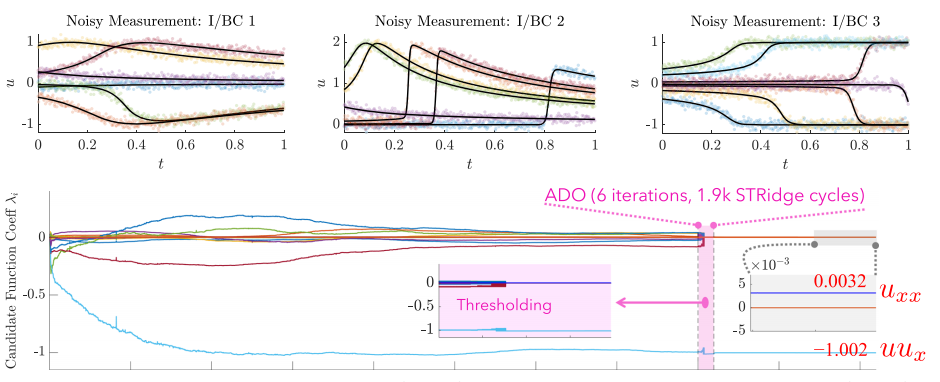
• 物理信息神经网络（PINN）与稀疏回归：提出了一种新方法，使用深度神经网络结合稀疏回归来从少量且嘈杂的数据中发现控制非线性时空系统的偏微分方程。

• 自动微分：利用深度神经网络的自动微分能力来准确计算解的导数，避免数值微分带来的挑战。

• 稀疏回归：通过稀疏回归来识别形成方程结构和显式表达式的关键导数项和参数。

• 交替方向优化（ADO）算法：提出了一种优化策略，将整体优化问题分解为一系列可处理的子问题，以顺序优化神经网络参数和稀疏PDE系数。

创新点

• 物理信息神经网络与稀疏回归的结合：这种方法整合了深度神经网络的丰富表示学习能力、自动微分的精确导数计算能力以及稀疏回归的高效方程识别能力。

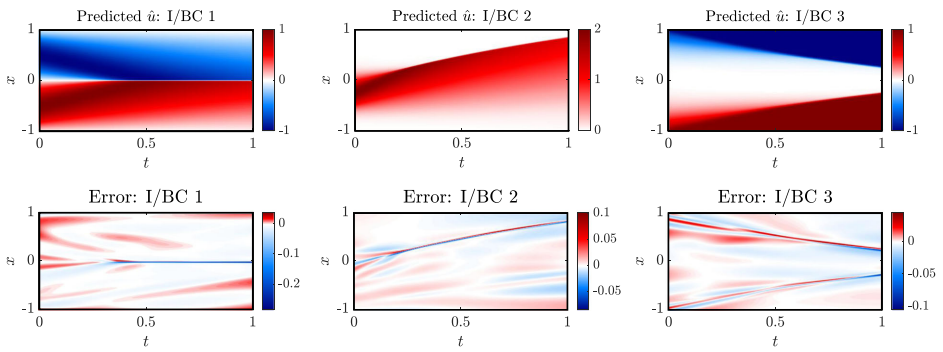
• 从少量且嘈杂的数据中学习：该方法能够处理实际应用中常见的数据稀缺和噪声问题，提高了模型在现实世界数据条件下的适用性。

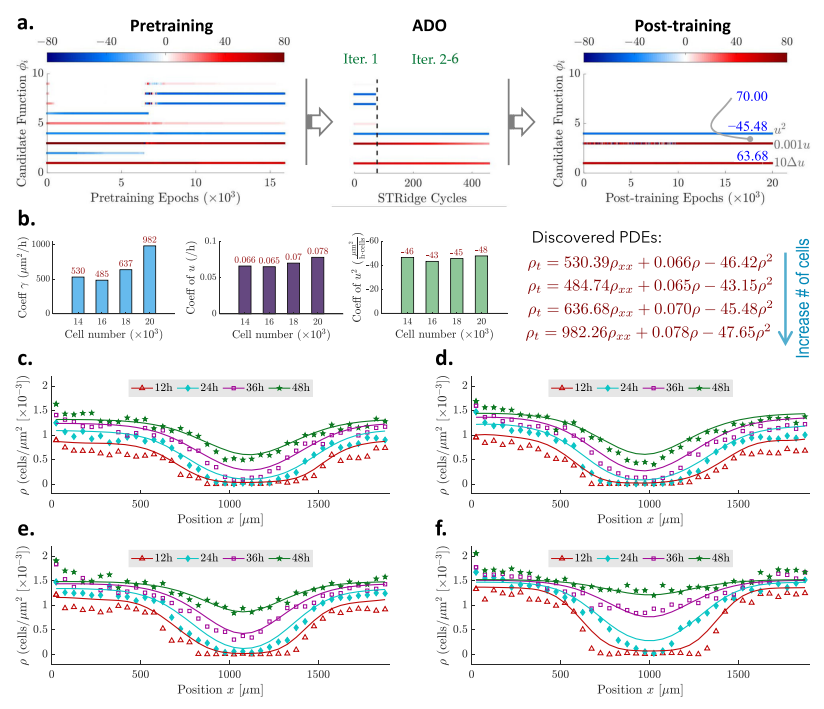
• “根-分支”网络架构：设计了一种新的网络架构，能够处理来自不同初始/边界条件的多个独立数据集，增强了模型的泛化能力。

• 交替方向优化策略：提出了一种新的优化策略，有效地处理了稀疏回归中的非光滑优化问题，提高了模型的优化效率和准确性。

---

论文2：

【Nature】Wavelets based physics informed neural networks to solve non-linear differential equations

基于小波的物理信息神经网络解决非线性微分方程

方法

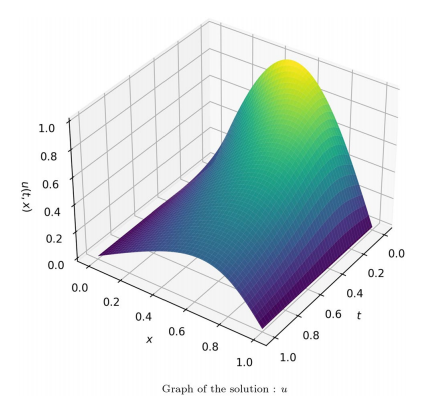
• 物理信息神经网络（PINN）：使用包含所有物理信息到损失函数中，构建一个近似解的神经网络。

• 小波激活函数：将小波作为激活函数，以提高神经网络的泛化能力。

• 自动微分技术：利用自动微分技术计算损失函数中的导数，简化了PINN中的重要步骤。

• 优化算法：使用Adam优化算法，结合了自适应梯度和均方根传播的优点，以提高训练效率。

创新点

• 小波激活函数的应用：在PINN中使用小波作为激活函数，提高了模型的学习和泛化能力。

• 多尺度和局部化特性：利用小波的多尺度和局部化特性，有效表示函数，使用更少的系数和更快的算法。

• 问题特定的神经网络设计：研究了神经网络设计中的关键因素，如网络架构、隐藏层数量、神经元数量对模型准确性的影响。

• 损失函数的改进：通过在损失函数中加入更多信息，提高了模型的性能，同时研究了动态权重分配对损失函数的影响。

---

论文3：

MetaNO: How to Transfer Your Knowledge on Learning Hidden Physics

MetaNO：如何传递学习隐藏物理知识

方法

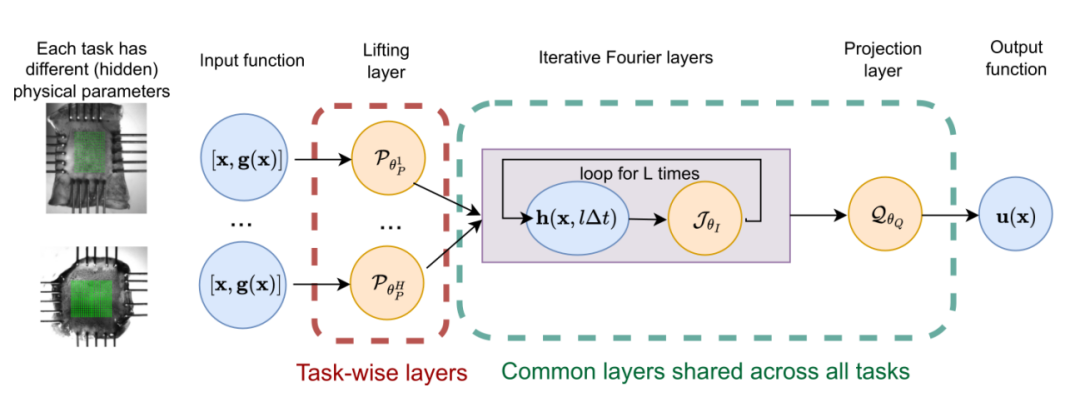
• 元学习神经算子（MetaNO）：提出了一种新颖的元学习方法，用于在不同的参数场之间传递解算子的知识。

• 参数场捕获：通过在神经算子模型的第一层中适应参数场，而不是在最后一层，来捕获底层参数场。

• 理论观察：发现参数场可以在神经算子模型的第一层中被捕获，这与传统的元学习方法不同。

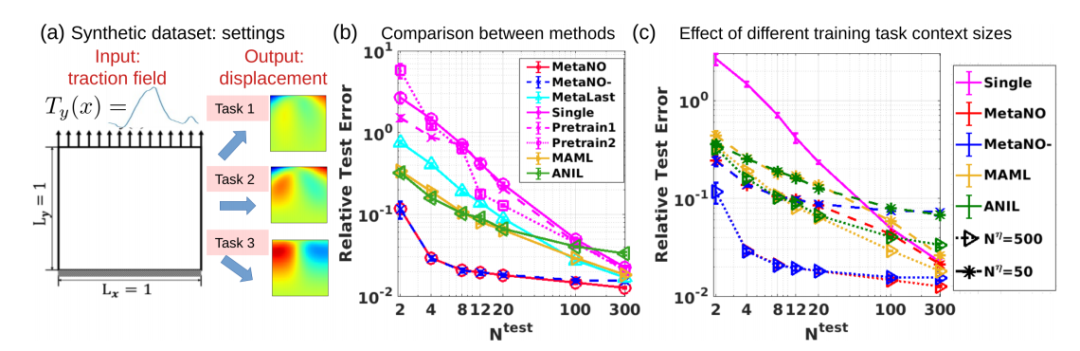
• 应用验证：在基于PDE的数据集和现实世界的材料建模问题上展示了所提方法的有效性。

创新点

• 第一层适应：与传统的元学习方法不同，MetaNO通过适应第一层而不是最后一层，更适合于PDE求解任务。

• 通用解算子：MetaNO作为一个可证明的通用解算子，能够处理多个PDE求解任务。

• 采样效率：在新任务上，MetaNO能够显著提高采样效率，与可比精度相比，节省了约90%的测量需求。

• 实际应用：在合成数据集、基准测试数据集和现实世界的生物组织数据集上，所提出的方法一致性地超越了现有的非元转移学习方法和其他基于梯度的元学习方法。

---

论文4：

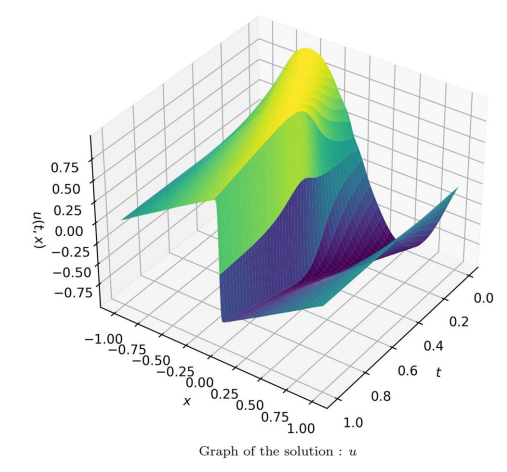
Monte Carlo Neural PDE Solver for Learning PDEs via Probabilistic Representation

通过概率表示学习PDEs的蒙特卡洛神经PDE求解器

方法

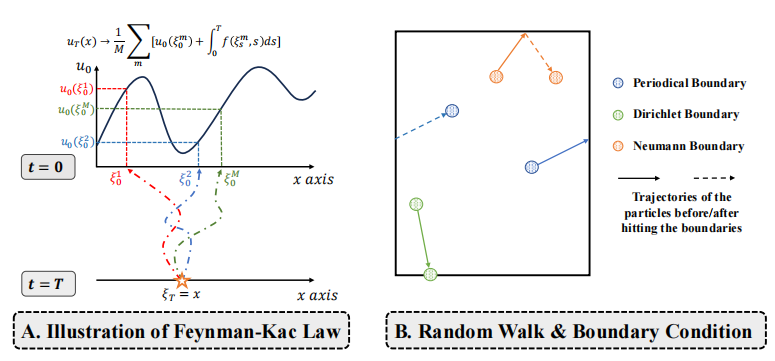
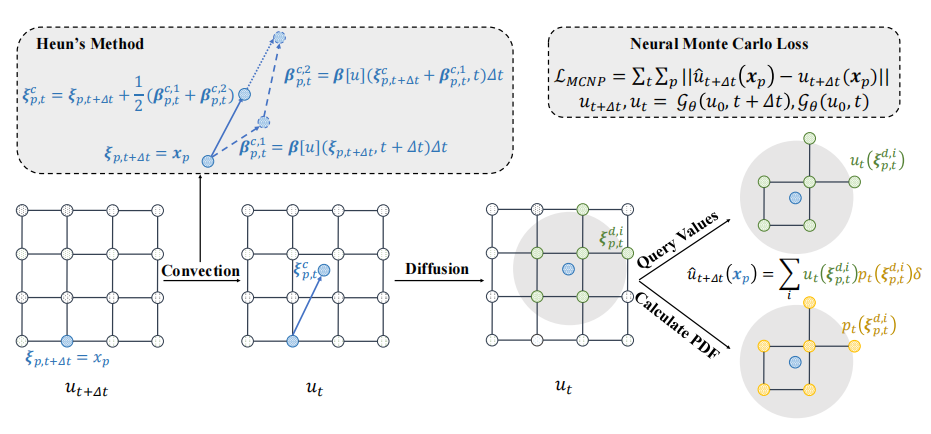
• 蒙特卡洛神经PDE求解器（MCNP求解器）：提出了一种通过PDEs的概率表示来训练无监督神经求解器的新方法。

• Heun方法：在模拟粒子轨迹的对流过程中使用Heun方法，以提高准确性。

• 概率密度函数（PDF）：在扩散过程中，通过邻近网格点的概率密度函数来计算期望值，避免了蒙特卡洛方法中大量粒子采样的需要。

创新点

• 概率表示：将宏观现象视为随机粒子的集合，为PDE系统提供了新的概率表示视角。

• 无监督学习：MCNP求解器能够在有限数据的情况下进行无监督训练，适用于数据稀缺的场景。

• 计算效率：通过避免精细的空间时间离散化，减少了计算挑战和累积误差，提高了模拟的准确性和效率。

• 处理高频率空间场：由于其无导数特性，MCNP求解器能够有效处理高频率空间场。

• 自动编码边界条件：边界条件被自然编码到粒子的随机过程中，消除了引入额外损失项以满足这些约束的需要。