素数几种方法（区间筛）

一、暴力

// 暴力
bool isprime(int n) {
	int i;
	// 对[2,sqrt(n)] 区间的数遍历判断，试除法 
	for(i = 2; i <= sqrt(n); i ++) { // i<=sqrt(n) 可以换成i*i<=n 
		if(n%i==0) return false;
	}
	return true; 
} 

二、埃式筛

缺陷是会出现重复筛选，例如 ：2*6 = 12   3*4 = 12  （质数2的六倍，和质数3的四倍，都是12）

所以只要最小最小质因子来筛选。就是下下面的欧拉筛。

// 埃式筛
//把不是素数的找出来，剩下的都是素数
//质数倍筛选
bool number[maxn+5];
void isprime() {
	int i, j;
	memset (number,true,sizeof number);
	for(i = 2; i <= maxn; j ++) {
		if(number[i]==true) { //是质数，开始质数倍筛选 
			for(j = 2; j*i<=maxn; j ++) //maxn是界内，防止j*i越界 
				number[i*j]=false; 
		}
	}
} 

三、欧拉筛

用最小质因子来筛（每个数只被最小质因子来筛去）

例如：已知质数2   那么2*2 = 4（质数2的2被筛去4） 2*3 = 6（质数2的三倍就不筛了）因为2%2==0。  6会被  3*2 给筛去（因为3%2！=0） 3*3 = 9 （3的质数被会筛去两个）

总之，6的质因子有 2 和 3，  那么，只会被2筛去， 也就是3的2倍筛去，一旦出现比3大的数，就不筛了，以免重复筛去。

代码1

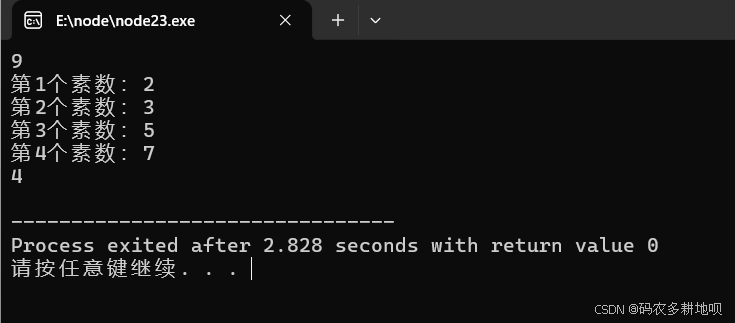
// 将 2- n 的素数按 排位 存起来 例如：2 3 5 7...... 
#include<bits/stdc++.h>
using namespace std;

const int maxn = 1e6+10;

int prime[maxn], cnt; //存素数
bool vis[maxn]; //筛选标记数组

void getprime(int n) {
	cnt = 0; // 存素数的索引 // 从0下标开始存 
	memset(vis,false,sizeof vis);//初始化为false
	memset(prime,0,sizeof prime);
	// 从2 - n
	for(int i = 2; i <= n; i ++) {
		//没有被筛掉，是素数，存起来
		if(!vis[i]) prime[cnt++] = i;
		for(int j = 0; j<cnt && i*prime[j]<=n; j ++) {
			// j指向数组里的素数，为了筛掉i的素数被的值
			// i*prime[j] <= n; 是为了防止数字i与素数prime[j] 乘积越界了
			vis[i*prime[j]] = true;
			if(i%prime[j]==0) break; // 只要最小质因子 例如 (i)3*2(prime[0]) = 6 
			//不要 （i)2*3(prime[1]) = 6, 6 只用prime[0] = 2 来筛去 
		}
	} 
} 

int main() {
	int n;
	scanf("%d",&n);
	getprime(n);
	for(int i = 0; i < cnt; i ++) {
		printf("第%i个素数：%d\n",i+1,prime[i]);
	} 
	printf("%d\n",cnt); //数组内存了cnt个素数 
	return 0;
} 

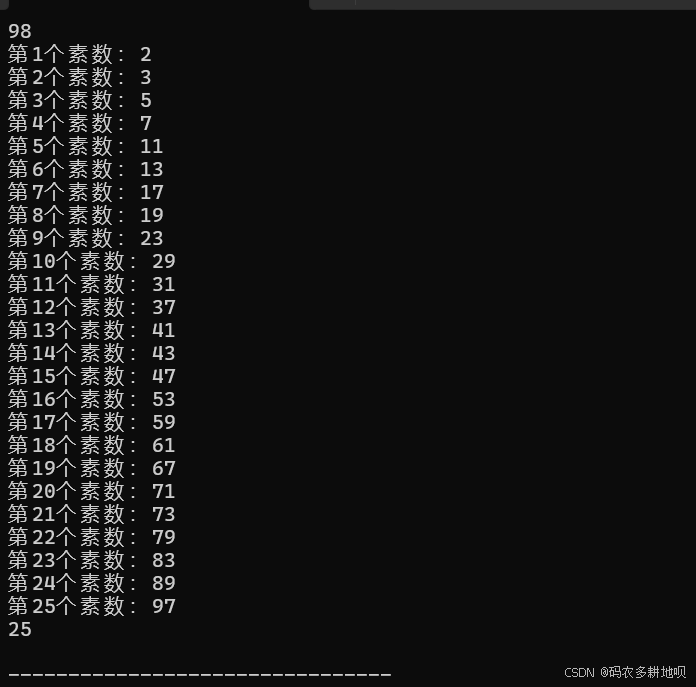
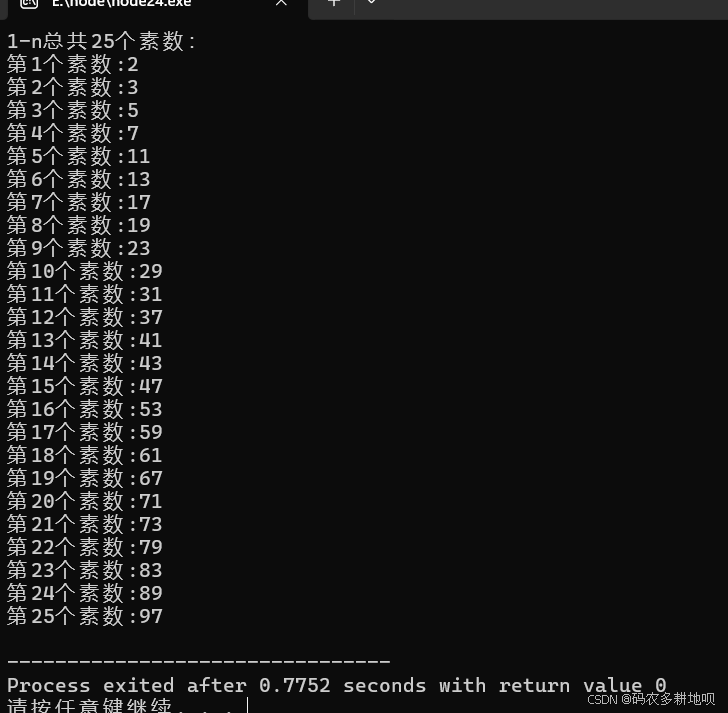
代码2（vector动态数组） 

// 2 - n的素数
#include<bits/stdc++.h>
using namespace std;

const int N = 1e6+10;
vector<int> prime;
vector<bool> vis(N); 

void get_prime(int n) {
	for(int i = 2; i <= n; i ++) {
		
		if(!vis[i]) prime.push_back(i); 
		
		for(int j = 0; j < prime.size(); j ++) {
			if(i*prime[j]>n) break; // 防越界 
			vis[i*prime[j]] = true;
			if(i%prime[j]==0) break;
		}
	}
}

int main() {
	puts("输入n:");
	int n;
	cin >> n;
	get_prime(n);
	
	printf("1-n总共%d个素数：\n",prime.size());
	 
	for(int i = 0; i < prime.size(); i ++) {
		cout << "第" << i+1 << "个素数:" << prime[i] << endl;
	}
	return 0; 
} 

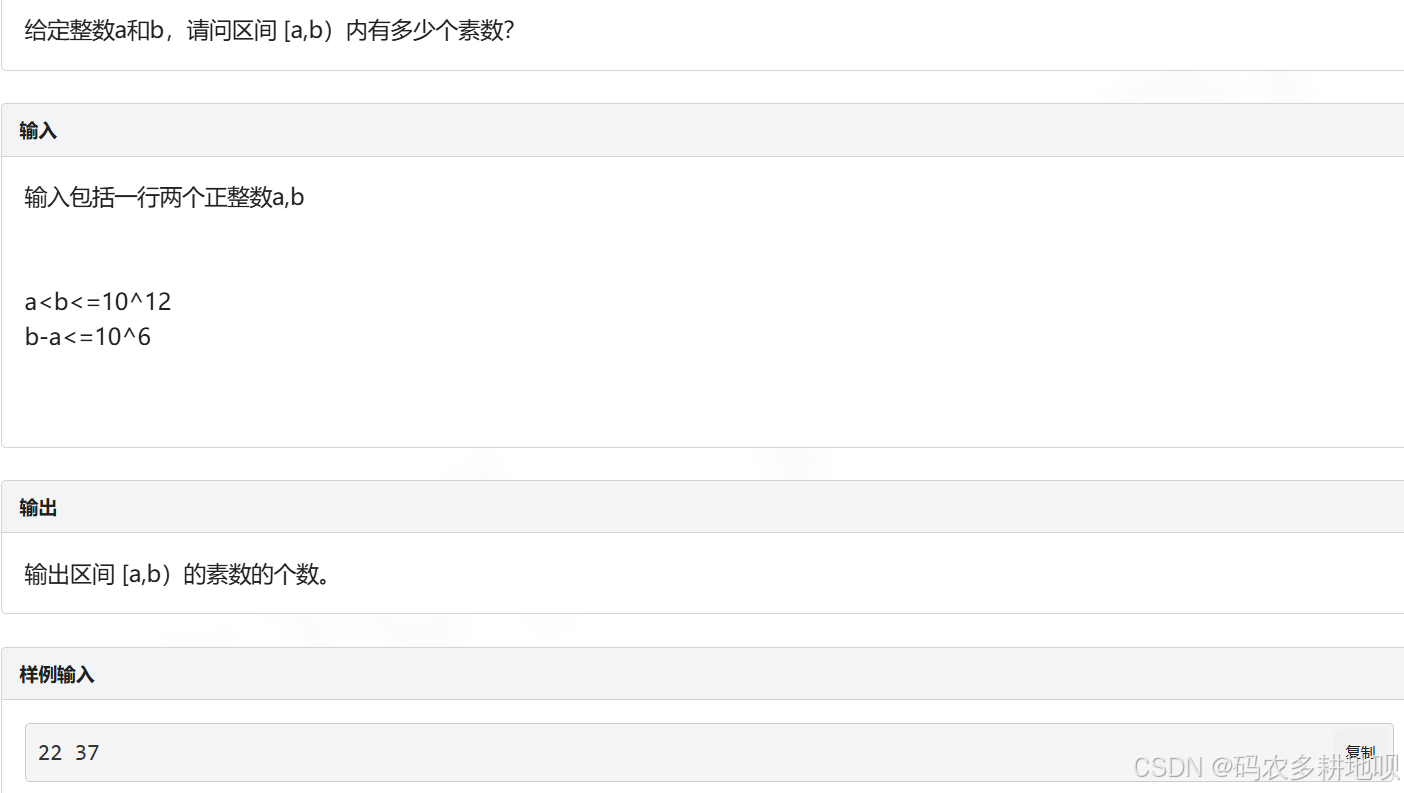
四、 区间筛（1e11内素数总数？）

代码1

 

// [a,b)内有多少素数？（a<b<=1e12, b-a<=1e6)

#include<bits/stdc++.h>
using namespace std;

typedef long long ll;
const int maxn = 1e6+7;
bool is_prime[maxn]; //【0,b-a) //偏移后区间 
bool is_prime_small[maxn]; //【2,sqrt(b)) //质因数 
ll prime[maxn]; //【a,b)  //所求区间 
ll num = 0; 

void segment_sieve(ll a, ll b) {
	for(ll i = 0; i*i < b; i ++) //【2,sqrt(b))的初始化为质数 true 
		is_prime_small[i] = true;
	for(ll i = 0; i < b-a; i ++) //下标偏移a 【a,b) 偏移a 【0,b-a)
		is_prime[i] = true;
		
	for(ll i = 2; i*i < b; i ++) { // 筛选【2,sqrt(b))
		if(is_prime_small[i]) {
			for(ll j = 2*i; j*j<b; j += i) //(筛掉i的倍数，从2*i开始到 界限前 
				is_prime_small[j] = false; //筛掉 
				
			ll maxx = 2;
			//最接近a的i的倍数，最小也是i*i倍
			for(ll j = max(maxx,(a+i-1)/i)*i; j < b; j += i) 
				is_prime[j-a] = false;
		} 
		
	} 
	for(ll i = 0; i < b-a; i ++) //统计个数
		if(is_prime[i])
			prime[num++] = i + a; 
}

int main() {
	ll a, b;
	cin >> a >> b;
	if(a==1) a=2;
	segment_sieve(a,b);
	
	//if(a==1) cout << num-1 << endl;  // a==1 会导致筛不掉 1 的位置。 
//	else
	 cout << num << endl;
	return 0;
}

例题

P1313 - 区间内素数的个数 - HAUEOJ

代码 2（四、区间筛的代码复制过去可以过）

c语言版本

#include<stdio.h>

#define N 1000007

long long max(long long a,long long b) {
	if(a>b) return a;
	else return b;
}

bool A[N]; // [2,sqrt(b) )
bool B[N]; // 【a,b)偏移后【0，b-a） 
long long prime[N]; // 存[a,b)的素数 
long long num = 0; // 【a,b)的索引，存素数的地方 

void solve(long long a, long long b) {
	// 初始化 a，b数组;
	// A筛选到 质 因子 （因子是质数） 
	for(long long i = 0; i*i<b; i ++) { // i*i<b 就是 i<sqrt(b) 
		A[i] = true; // 初始化为质数 
	} 
	// 通过A来筛选 B中质数，原理是质因子的倍数筛除法 
	for(long long i = 0; i < b-a; i ++) {
		B[i] = true;
	}
	
	//开始筛除
	for(long long i = 2; i*i < b; i ++) {
		
		if(A[i]) { // 是质数开始 筛除 A B 
			for(long long j = i*2; j*j<b; j +=i) {
				A[j] = false;
			}
			//最接近a的i的倍数 （有文字解析）
			long long maxx = 2; // 最小也是从 2*i 开始筛除 
			for(long long j = max(maxx,(a+ i-1 )/i)*i; j<b; j += i) {
				B[j-a] = false; // 下标偏移j-a 
			}
		}
		
	} 
	// 存[a,b)数组 并统计个数 
	// 通过[0,b-a) 偏移回 
	for(long long i = 0; i < b-a; i ++) {
		if(B[i]) prime[num++] = i+a;
	} 
	
}

int main() {
	long long a, b;
	// 筛选不掉 a = 1的情况，会导致 1 也是素数
	//人工操作，去掉a = 1， 因为都是从 2的倍数开始筛除
	scanf("%lld%lld",&a,&b);
	if(a==1) a =2;
	
	solve(a,b);
	
	printf("%d\n",num);
	return 0;
}