从递归到递推--入门篇

从递归到递推–入门篇

一.1.什么是递归

递归是指一种通过重复将问题分解为子问题而解决问题的方法。具体到使用上来，就是指对函数自身的调用。本文所讨论的递归，都是基于函数对自身的调用。但是，递归并非仅对函数而言，递归是种思想，例如C语言中的链表的实现同样依托递归思想，本文在此就不做展开了。

一.2.递归是如何实现的

顾名思义，递归分为“递”和“归”。递是反复调用函数的过程，归就是函数调用结束后返回的过程。下面我们举一个例子来更好地理解这一过程。

#include<stdio.h>
int sum(int n) {
    if(n==0) return n;
    else return n+sum(n-1);
}
int main() {
    int a=5;
    printf("%d",sum(a));
}

这是一个简单的求和代码，从5依次加到1

而’"递"的过程是5+sum(4)–>5+4+sum(3)–>5+4+3+sum(2)–>5+4+3+2+sum（1）–>5+4+3+2+1+sum（0）直到n=0时结束调用。

此时开始进行函数返回，返回到函数被调用的地方 5+（4+（3+（2+1）））–>5+(4+(3+3))–>5+(4+6)–>5+10–>15结束

对于初学者可能不理解“归”的过程，层层返回绕的人头大。但是搞清“递”的过程，正确判断出每次调用后“递“到哪个return后面，最后到终止条件结束，返回到调用函数的主函数中，也能初步理解递归的思想了。从这个简单的递归代码中，我们应该能找出递归三个不可或缺的要素。

1. 找出递归关系式，此例中是一个简单的求和递归，每次调用函数的参数为上一个数减一即可。

2. 递归终止条件，此例中即为n=0，当n=0时返回主函数中，终止函数调用。

3. 给出递归终止的处理办法，此例直接返回到主函数中。

   一.3.递归的优势

   上面的例子显然没有表现出递归的优势，我们下面用辗转相除法求最大公约数来简单认识一下递归的强大功能

   辗转相除法–假设两数a,b且a>b，用a/b，能除尽则b是最大公因数。否则令a=b,b=余数，循环a/b直到除尽。

   #include <stdio.h>
   int div(int a,int b) {
       if(a%b==0) return b;
       else return div(b,a%b);
   }
   int main(void)
   {
       int a=0,b=0;
       scanf("%d %d",&a,&b);
       printf("%d",div(a,b));
   }
   

用递归写辗转相除法，一方面简化代码简洁明了，另一方面减少变量使用，避免对额外内存空间的需求，提高运行速度。

对于这样一个简单的程序，递归显然占尽优势，但是递归由于对自身反复的调用，在很多问题上会导致重复计算拖慢速度，

那么自然就引出了下面的问题–

一.4.递归的缺点

来看这样一个程序（我们实验室的一面题，当时不会的那道题）

#include<stdio.h>
int **function**(int n){

if (n < 5)   return n;

else   return **function**(n-1) + **function**(n-3);

}

int main(){

int n=10;

**printf**("%d\n", function(n));

return 0;

}

下面是递归的过程

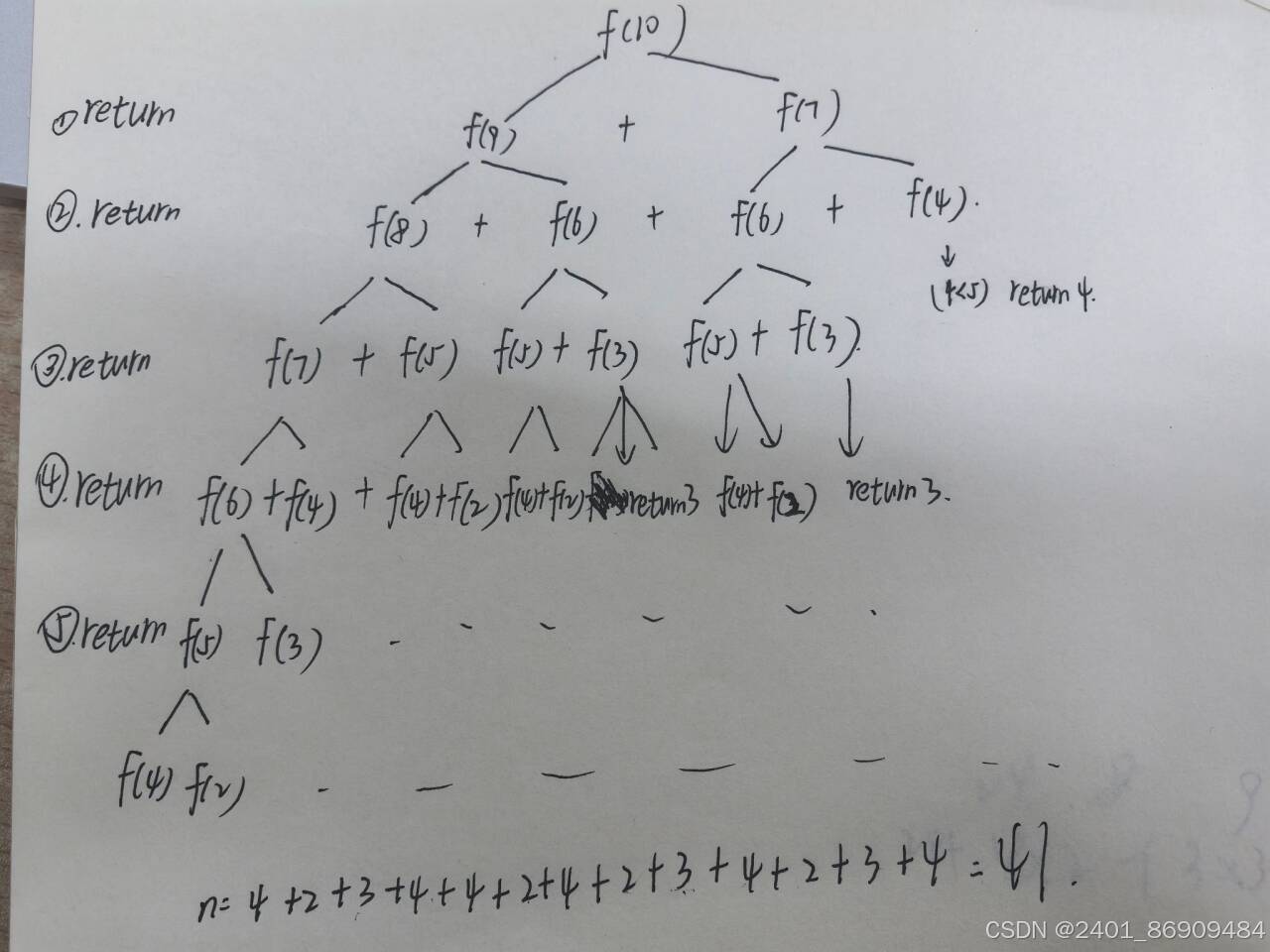
可以看到，函数反复地计算f(3)，f(4)的值。这个程序运算简单所以计算机仍能迅速得到41的结果，但是随着初始值n的增大，这样的重复计算会明显导致效率降低。例如在对于兔子数列（斐波那契数列）的问题中

一对兔子，从出生后第3个月起每个月都生一对兔子。小兔子长到第3个月后每个月又生一对兔子。假如兔子都不死，请问从第1个月起，繁衍到第n个月时兔子总数多少对

斐波那契数列，即从第三项开始，每一项都等于前两项数之和

此时如果用递归的方法，那么就会像前面一例的计算一样，越往后面计算越是繁琐，当n=40左右时程序速度已经放慢了。此时便引入另一种思想，即递推

---

---

二.递推

递推的定义是用若干步重复运算来描述复杂问题的方法，按一定规律计算数列中的每个项。

具体到C语言应用上，就是找规律，如题

月份	1	2	3	4	5	6
兔子数量	1	1	2	3	5	8

当我们发现规律，可以直接创建一个数组记录前两个月的兔子数，第三个月的数量就等于前两个数组之和，这样显然比递归的重复计算快了很多。

int a[50];
for(int i=2;i<50;i++) {
    a[i]=a[i-1]+a[i-2];
}

因此，相对于递归，递推并不难理解，只是一项一项地找规律并表示出来

---

三.递推与递归

从上述对两者的介绍，可以发现递推与递归可以相互转化。前者按一定的关系式逐步推导出解，后者反复调用自身解决问题。递归元素之间的关系是就是递推表达式。

最后，如果对于递归的理解仍然不清楚，可以在自己的编译器上将前面几个简单的递归代码进行逐步调试，自己动手丰衣足食。