cs285 lecture 6

CS285 持续更新
👉 GitHub仓库直达： https://github.com/CalebCheng819/cs285 (记得复制完整链接哦！ )可以给个🌟吗

lecture 6

part1

我们定义state-action和state函数

$Q^{\pi }\left({\mathbf{s}}_t,{\mathbf{a}}_t\right)={\sum }_{t^{\prime }=t}^T{E}_{{\pi }_{\theta }}\left[r\left({\mathbf{s}}_{t^{\prime }},{\mathbf{a}}_{t^{\prime }}\right)\mid {\mathbf{s}}_t,{\mathbf{a}}_t\right]$ : total reward from taking ${\mathbf{a}}_t$ in ${\mathbf{s}}_t$
$V^{\pi }\left({\mathbf{s}}_t\right)=E_{{\mathbf{a}}_t\sim {\pi }_{\theta }\left({\mathbf{a}}_t\mid {\mathbf{s}}_t\right)}\left[Q^{\pi }\left({\mathbf{s}}_t,{\mathbf{a}}_t\right)\right]:$ total reward from ${\mathbf{s}}_t$

在此基础上，我们在定义一个advantage function
$$A^{\pi }\left({\mathbf{s}}_t,{\mathbf{a}}_t\right)=Q^{\pi }\left({\mathbf{s}}_t,{\mathbf{a}}_t\right)-V^{\pi }\left({\mathbf{s}}_t\right)\text{ : how much better }{\mathbf{a}}_t\text{ is }$$
于是我们可以得到
$$Q^{\pi }({\mathbf{s}}_t,{\mathbf{a}}_t)=r({\mathbf{s}}_t,{\mathbf{a}}_t)+E_{{\mathbf{s}}_{t+1}\sim p({\mathbf{s}}_{t+1}|{\mathbf{s}}_t,{\mathbf{a}}_t)}[V^{\pi }({\mathbf{s}}_{t+1})]\approx r({\mathbf{s}}_t,{\mathbf{a}}_t)+V^{\pi }({\mathbf{s}}_{t+1})$$

$$A^{\pi }({\mathbf{s}}_t,{\mathbf{a}}_t)\approx r({\mathbf{s}}_t,{\mathbf{a}}_t)+V^{\pi }({\mathbf{s}}_{t+1})-V^{\pi }({\mathbf{s}}_t)$$

advantage function和state-action function都与action和state都有关系，而value function只与状态有关系

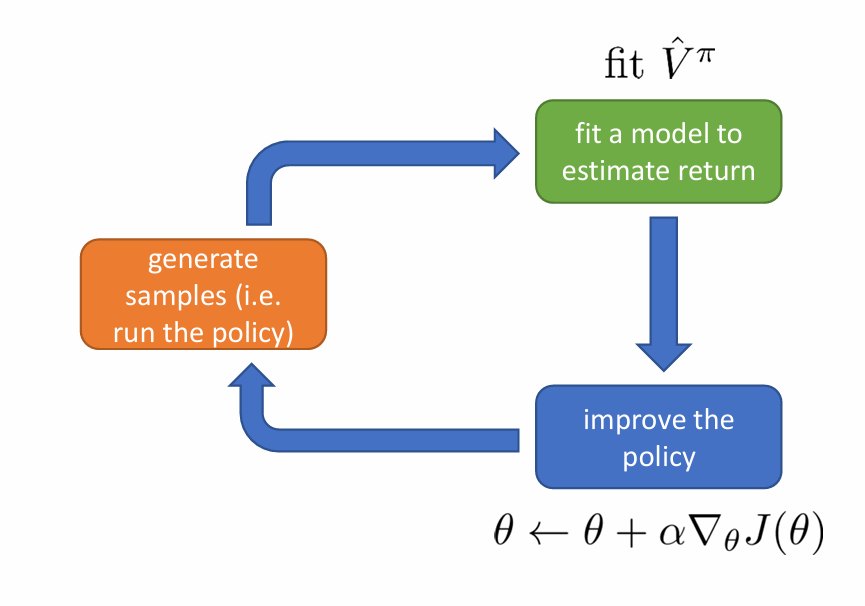
Monte Carlo policy function

对于单条轨迹来说
$$V^{\pi }({\mathbf{s}}_t)\approx \sum _{t^{\prime }=t}^{T}r({\mathbf{s}}_{t^{\prime }},{\mathbf{a}}_{t^{\prime }})$$
多轨迹采样
$$V^{\pi }({\mathbf{s}}_t)\approx \frac{1}{N}\sum _{i=1}^N\sum _{t^{\prime }=t}^{T}r({\mathbf{s}}_{t^{\prime }},{\mathbf{a}}_{t^{\prime }})$$
虽然单轨迹时候效果不如多轨迹，但仍然pretty good，在数据有限的时候仍然可以使用

bootstrapped

$$y_{i,t}=\sum _{t^{\prime }=t}^T{E}_{{\pi }_{\theta }}\left[r({\mathbf{s}}_{t^{\prime }},{\mathbf{a}}_{t^{\prime }})|{\mathbf{s}}_{i,t}\right]\approx r({\mathbf{s}}_{i,t},{\mathbf{a}}_{i,t})+V^{\pi }({\mathbf{s}}_{i,t+1})\approx r({\mathbf{s}}_{i,t},{\mathbf{a}}_{i,t})+{\hat{V}}_{\varphi }^{\pi }({\mathbf{s}}_{i,t+1})$$

这时候的训练数据就变成了
$$\left\{\left({\mathbf{s}}_{i,t},r({\mathbf{s}}_{i,t},{\mathbf{a}}_{i,t})+{\hat{V}}_{\varphi }^{\pi }({\mathbf{s}}_{i,t+1})\right)\right\}$$
相比蒙特卡洛方法，这种方法通常方差更小但可能更有偏差

part2

discount factors

对于episode length为无穷的，${\hat{V}}_{\varphi }^{\pi }$会变得非常大，所以我们这里引入一个simple trick——discount factor
$$y_{i,t}\approx r({\mathbf{s}}_{i,t},{\mathbf{a}}_{i,t})+\gamma {\hat{V}}_{\varphi }^{\pi }({\mathbf{s}}_{i,t+1})$$
其中$$\gamma \in [0,1]$$，0.99works well，$\gamma$会改变MDP的结构，对于每个时间步来说有$1-\gamma$的概率终止episode

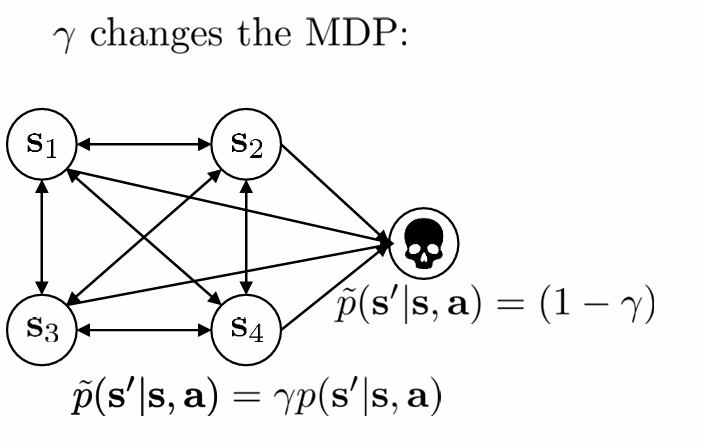
对于actor-critic来说，我们可以引入discount factor写成
$$\begin{array}{rl}& {\nabla }_{\theta }J(\theta )\approx \frac{1}{N}\sum _{i=1}^N\sum _{t=1}^T{\nabla }_{\theta }\log {\pi }_{\theta }\left({\mathbf{a}}_{i,t}\mid {\mathbf{s}}_{i,t}\right)(\overbrace{r\left({\mathbf{s}}_{i,t},{\mathbf{a}}_{i,t}\right)+\gamma {\hat{V}}_{\varphi }^{\pi }\left({\mathbf{s}}_{i,t+1}\right)-{\hat{V}}_{\varphi }^{\pi }\left({\mathbf{s}}_{i,t}\right)})\end{array}$$
那么，对于Monte Carlo来说，有以下option，只用其中两个是正确的

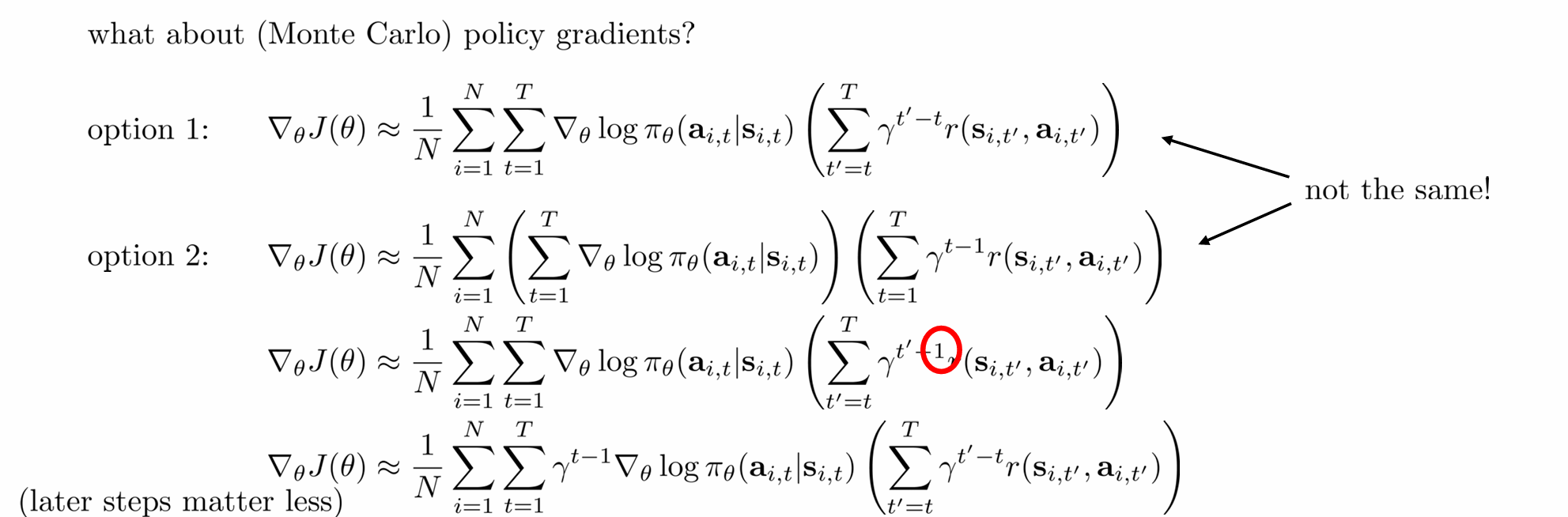
其中option2中的第一个它不是逐步计算，而是整体地计算策略对所有动作的 log-prob，再乘一个全局回报加权，这样的梯度是错误的估计

option2中的第二个，把 reward-to-go 部分的权重换成 ${\gamma }^{t-1}$，就错了！因为折扣应该是相对当前 $t$ 的未来奖励，而不是绝对时间

但是，在实际使用中我们会使用option1，因为我们需要的一个一直好下去的动作，而不是只关注早期的行为
$${\nabla }_{\theta }J(\theta )\approx \frac{1}{N}\sum _{i=1}^N\sum _{t=1}^T{\nabla }_{\theta }\log {\pi }_{\theta }({\mathbf{a}}_{i,t}|{\mathbf{s}}_{i,t})\left(\sum _{t^{\prime }=t}^T{\gamma }^{t^{\prime }-t}r({\mathbf{s}}_{i,t^{\prime }},{\mathbf{a}}_{i,t^{\prime }})\right)$$

actor-critic algorithm

actor负责策略${\pi }_{\theta }$，选择动作。critic负责评估状态价值，引入advantage function计算策略梯度

对比维度	Batch Actor-Critic	Online Actor-Critic
数据收集方式	先收集一批数据（batch），再更新策略	单步交互后立即更新
计算效率	计算开销较大（需存储整个batch）	计算开销较小（单步更新）
样本相关性	数据相关性高（同一批数据多次使用）	数据相关性低（单步数据）
训练稳定性	更稳定（梯度基于大量数据计算）	波动较大（单步数据噪声大）
适用场景	适用于离线学习、仿真环境	适用于实时学习、机器人控制
探索能力	依赖batch数据，探索可能不足	可实时调整策略，探索性更强
实现复杂度	需要存储和管理batch数据	实现更简单，无需存储历史数据

part3

architecture design

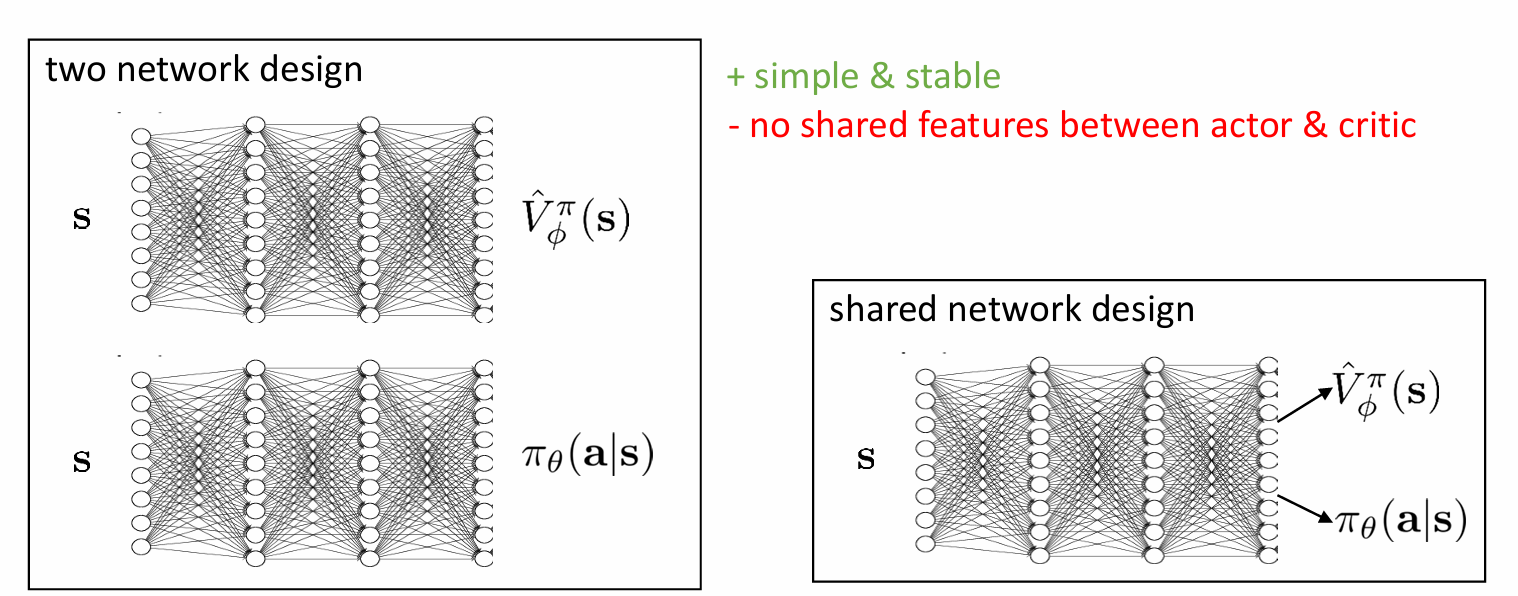
使用两个网络的优势是容易训练且稳定，缺点是没有共享feature，导致参数量增大，计算量也增大。而使用一个网络解决了两个网络的优势，但是有可能会出现两个部分冲突的问题。

并行化（Parallel Workers）

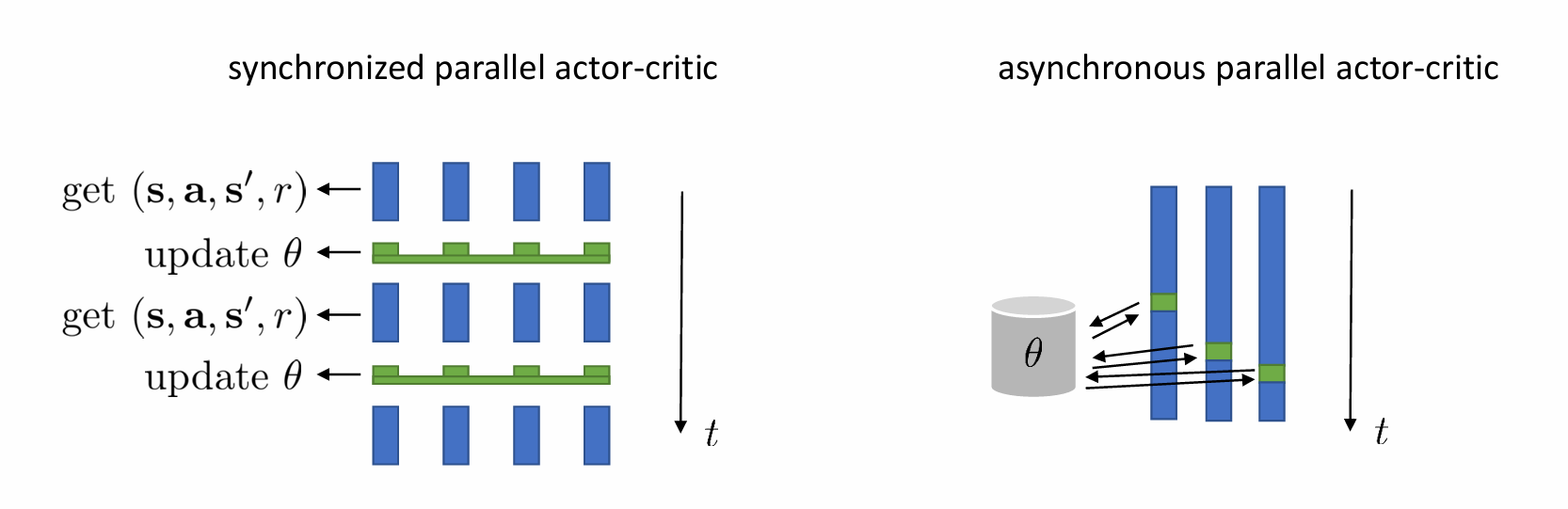
1. 同步并行 Actor-Critic（Synchronized Parallel）
   • 多个 Worker 同时与环境交互，收集数据。
   • 同步更新：所有 Worker 完成一批数据后，统一计算梯度并更新策略。
   • 优点：训练稳定，适用于分布式计算（如 A3C 的同步版本）。
   • 缺点：速度受最慢 Worker 限制。
2. 异步并行 Actor-Critic（Asynchronous Parallel, A3C）
   • 每个 Worker 独立与环境交互，并 异步更新 全局策略。
   • 优点：更快（无需等待所有 Worker），适用于多 CPU/GPU。
   • 缺点：可能因异步更新导致策略震荡（需调整学习率）。

online actor-critic

上述算法流程图中存在两个问题：

1. 这是 on-policy 算法（如 A2C、PPO），要求数据必须来自当前策略 πθ，所以针对当前动作，我们应该采取state-action function，即修改
   $$y_i=r_i+\gamma {\hat{Q}}_{\varphi }^{\pi }\left(s_i^{\prime },a_i^{\prime }\right),a_i^{\prime }\sim {\pi }_{\theta }\left(a_i^{\prime }\mid s_i^{\prime }\right)$$
   然后最小化均方误差（也是用Q function）
   $$\mathcal{L}(\varphi )=\frac{1}{2}\sum _i{\Vert {\hat{Q}}_{\varphi }^{\pi }\left(s_i,a_i\right)-y_i\Vert }^2$$

2. 回放缓冲区 RR 中的动作 $a_i$来自历史策略，但梯度计算假设它们来自当前策略 ${\pi }_{\theta }$（即 未修正策略差异）。

   当然，我么可以考虑从当前策略${\pi }_{\theta }$重新采样，但需额外采样，计算成本高。

   所以在实际操作中，可以考虑直接用Q function近似处理，依赖Q函数的准确性（具体到动作）
   $${\nabla }_{\theta }J(\theta )\approx \frac{1}{N}\sum _i{\nabla }_{\theta }\log {\pi }_{\theta }\left({\mathbf{a}}_i^{\pi }\mid {\mathbf{s}}_i\right){\hat{Q}}^{\pi }\left({\mathbf{s}}_i,{\mathbf{a}}_i^{\pi }\right)$$
   虽然这么操作会导致high variance，但是可以通过通常依赖大量采样平均。

当然除了上面两个明显的问题以外，仍然存在一定问题。

理想情况下，这个 $s_i$ 应该来自于当前策略 ${\pi }_{\theta }$ 所诱导的状态分布 $p_{\theta }(s)$。

也就是说，$p_{\theta }(s)$ 是“我们当前策略运行时会遇到的状态分布”。

但实际中，这些 $s_i$ 是从经验池 $\mathcal{R}$ 中采样的，可能来自：

• 旧版本策略 ${\pi }_{{\theta }_{old}}$；
• 各种 exploration noise；
• 甚至是 warm-up 初始策略。

这导致了一个重要的问题：

我们训练出来的策略 ${\pi }_{\theta }$ 不是在 $p_{\theta }(s)$ 上最优的，而是在一个更宽泛（broader）的状态分布上最优。

强化学习的目标是：
$$\underset{\theta }{\max }{\mathbb{E}}_{s\sim p_{\theta }(s),a\sim {\pi }_{\theta }(a|s)}[r(s,a)]$$
但我们实际优化的是：
$${\mathbb{E}}_{s\sim \mathcal{R},a\sim {\pi }_{\theta }(a|s)}[r(s,a)]$$
但，我们并无法解决，因为状态是不可控的 —— 我们不能直接从 $p_{\theta }(s)$ 中采样；实际上我们甚至都不知道 $p_{\theta }(s)$ 是什么；

在接下来的课程我们会讨论一些:

可以把随机采样 $a\sim {\pi }_{\theta }(a|s)$ 变成“可导”的形式：
$$a=f_{\theta }(ϵ;s),ϵ\sim \mathcal{N}(0,1)$$

• 这样可以直接对 $a$ 求导数，而不是用 log-derivative trick。
• 例如在 Soft Actor-Critic (SAC) 中使用了这个技巧。

也会学习用 确定性策略（如 DDPG、TD3）来替代当前的随机策略 ${\pi }_{\theta }(a|s)$，它们不需要从策略中采样动作，而是直接输出一个 deterministic action：$a={\mu }_{\theta }(s)$。

part4

critics as baseline

state dependent baseline

截至目前，我们学习了actor-critic
$${\nabla }_{\theta }J(\theta )\approx \frac{1}{N}\sum _{i=1}^N\sum _{t=1}^T{\nabla }_{\theta }\log {\pi }_{\theta }({\mathbf{a}}_{i,t}|{\mathbf{s}}_{i,t})\left(r({\mathbf{s}}_{i,t},{\mathbf{a}}_{i,t})+\gamma {\hat{V}}_{\varphi }^{\pi }({\mathbf{s}}_{i,t+1})-{\hat{V}}_{\varphi }^{\pi }({\mathbf{s}}_{i,t})\right)$$
以及policy gradient
$${\nabla }_{\theta }J(\theta )\approx \frac{1}{N}\sum _{i=1}^N\sum _{t=1}^T{\nabla }_{\theta }\log {\pi }_{\theta }({\mathbf{a}}_{i,t}|{\mathbf{s}}_{i,t})\left(\left(\sum _{t^{\prime }=t}^T{\gamma }^{t^{\prime }-t}r({\mathbf{s}}_{i,t^{\prime }},{\mathbf{a}}_{i,t^{\prime }})\right)-b\right)$$
其中actor-critic具有lower variance但可能有偏（如果critic is not perfect），policy gradient具有no bias，但是higher variance（single-sample estimate）

于是我们提出两者结合的无偏状态基线
$${\nabla }_{\theta }J(\theta )\approx \frac{1}{N}\sum _{i=1}^N\sum _{t=1}^T{\nabla }_{\theta }\log {\pi }_{\theta }({\mathbf{a}}_{i,t}|{\mathbf{s}}_{i,t})\left(\underset{\text{蒙特卡洛回报}}{\underbrace{\left(\sum _{t^{\prime }=t}^T{\gamma }^{t^{\prime }-t}{r}_{t^{\prime }}\right)}}-\underset{\text{状态相关基线}}{\underbrace{{\hat{V}}_{\varphi }^{\pi }({\mathbf{s}}_{i,t})}}\right)$$
这样子不仅无偏，且lower variance

action dependent baseline

首先引入一个控制变量的核心思想：

• 设 $X$ 是我们想要估计的随机变量（高方差）
• 设 $Y$ 是与 $X$ 相关的另一个随机变量（已知期望 $\mathbb{E}[Y]$ ）
• 构造新估计量：

$$Z=X-c(Y-\mathbb{E}[Y])$$

其中 $c$ 是待优化的系数

关键性质：

1. 无偏性： $\mathbb{E}[Z]=\mathbb{E}[X]$（因为 $\mathbb{E}[Y-\mathbb{E}[Y]]=0$ ）
2. 方差缩减：当 $X$ 和 $Y$ 高度相关时， $\mathrm{Var}(Z)<\mathrm{Var}(X)$
3. 最优系数：$c^{\ast }=\frac{\mathrm{Cov}(X,Y)}{\mathrm{Var}(Y)}$ 时方差最小

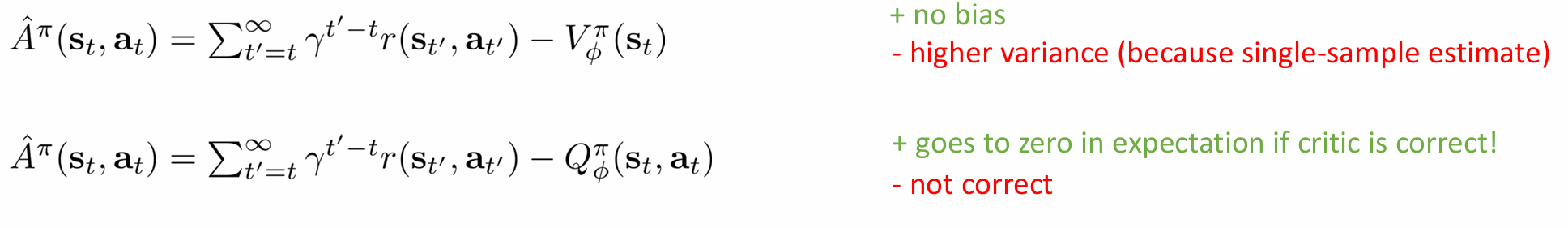
Q-Prop 提出了一种无偏的梯度估计器：
$$\begin{array}{rl}{\nabla }_{\theta }J(\theta )& \approx \underset{\text{带控制变量的蒙特卡洛估计 }}{\underbrace{\frac{1}{N}\sum _{i=1}^N\sum _{t=1}^T{\nabla }_{\theta }\log {\pi }_{\theta }\left(a_{i,t}\mid s_{i,t}\right)\left({\hat{Q}}_{i,t}-Q_{\varphi }^{\pi }\left(s_{i,t},a_{i,t}\right)\right)}}\\ & +\underset{\text{基于 Critic 的策略梯度 }}{\underbrace{\frac{1}{N}\sum _{i=1}^N\sum _{t=1}^T{\nabla }_{\theta }{\mathbb{E}}_{a_t\sim {\pi }_{\theta }}\left[Q_{\varphi }^{\pi }\left(s_{i,t},a_t\right)\right]}}\end{array}$$
其中：
$-{\hat{Q}}_{i,t}$ 是蒙特卡洛估计的动作价值（即从时刻 t 到轨迹结束的累积奖励）。
$-Q_{\varphi }^{\pi }\left(s_{i,t},a_{i,t}\right)$ 是Critic对动作价值的估计。

根据控制变量的核心思想，Q－Prop 的梯度估计器可重写为：
$${\nabla }_{\theta }J=\underset{\text{控制变量项 }}{\underbrace{\mathbb{E}\left[{\nabla }_{\theta }\log {\pi }_{\theta }\cdot \left(\hat{Q}-Q_{\varphi }^{\pi }\right)\right]}}+\underset{\text{Critic 主导项 }}{\underbrace{\mathbb{E}\left[{\nabla }_{\theta }{\mathbb{E}}_a\left[Q_{\varphi }^{\pi }\right]\right]}}$$

• 当 Critic 完美时 $\left(Q_{\varphi }^{\pi }=Q^{\pi }\right)$ ，第一项方差为零
• 当 Critic 较差时，第一项仍提供无偏的蒙特卡洛估计

eligibility traces&n-step returns

n 步优势函数估计是强化学习中平衡偏差-方差权衡的核心技术
$${\hat{A}}_n^{\pi }({\mathbf{s}}_t,{\mathbf{a}}_t)=\sum _{t^{\prime }=t}^{t+n}{\gamma }^{t^{\prime }-t}r({\mathbf{s}}_{t^{\prime }},{\mathbf{a}}_{t^{\prime }})-{\hat{V}}_{\varphi }^{\pi }({\mathbf{s}}_t)+{\gamma }^n{\hat{V}}_{\varphi }^{\pi }({\mathbf{s}}_{t+n})$$

项	数学表达式	物理意义	特性
实际奖励项	${\sum }_{k=0}^{n-1}{\gamma }^k{r}_{t+k}$	前 n 步的真实环境奖励	无偏但高方差
价值预测项	${\gamma }^n{\hat{V}}_{\varphi }^{\pi }\left(s_{t+n}\right)$	Critic 对 n 步后状态的估值	低方差但可能有偏
基线项	$-{\hat{V}}_{\varphi }^{\pi }\left(s_t\right)$	当前状态价值基准	降低方差，保持中心化

广义优势估计 (GAE) 是强化学习中用于平衡偏差-方差权衡的革命性技术它通过指数加权（可以视作discount factor）融合不同时间尺度的优势估计，解决了传统 n 步方法需要手动选择步长的痛点。

首先，我们给出state-action，state，advantage function的parameter$\gamma$形式
$$\begin{array}{rl}{V}^{\pi ,\gamma }\left(s_t\right)& :={\mathbb{E}}_{\begin{array}{c}{s}_{t+1:\infty },a_{t:\infty }\end{array}},\left[\sum _{l=0}^{\infty }{\gamma }^l{r}_{t+l}\right]Q^{\pi ,\gamma }\left(s_t,a_t\right):={\mathbb{E}}_{\begin{array}{c}{s}_{t+1:\infty },a_{t+1:\infty }\end{array}}\left[\sum _{l=0}^{\infty }{\gamma }^l{r}_{t+l}\right]\\ A^{\pi ,\gamma }\left(s_t,a_t\right)& :=Q^{\pi ,\gamma }\left(s_t,a_t\right)-V^{\pi ,\gamma }\left(s_t\right).\end{array}$$
引用原论文中的一个定义

Definition 1. The estimator ${\hat{A}}_t$ is $\gamma$-just if
$${\mathbb{E}}_{\begin{array}{c}{s}_{0:\infty }\\ a_{0:\infty }\end{array}}\left[{\hat{A}}_t\left(s_{0:\infty },a_{0:\infty }\right){\nabla }_{\theta }\log {\pi }_{\theta }\left(a_t\mid s_t\right)\right]={\mathbb{E}}_{\begin{array}{c}{s}_{0:\infty }\\ a_{0:\infty }\end{array}}\left[A^{\pi ,\gamma }\left(s_t,a_t\right){\nabla }_{\theta }\log {\pi }_{\theta }\left(a_t\mid s_t\right)\right]$$

核心任务是对折扣优势函数 $A^{\pi ,\gamma }\left(s_t,a_t\right)$ 进行准确估计，得到 ${\hat{A}}_t$ ，并将其用于构建策略梯度估计器，具体内容如下：
$$\hat{g}=\frac{1}{N}\sum _{n=1}^N\sum _{t=0}^{\infty }{\hat{A}}_t^n{\nabla }_{\theta }\log {\pi }_{\theta }\left(a_t^n\mid s_t^n\right)$$
定义 带折扣因子的TD时序差分残差（Temporal Difference Error）：
$${\delta }_t^V=r_t+\gamma {\hat{V}}_{t+1}-{\hat{V}}_t$$

TD 残差 ${\delta }_t^V$ 可被视为动作 $a_t$ 的优势估计。实际上，当价值函数 $V$ 完全准确（即 $V=V^{\pi ,\gamma }$ ，与策略 $\pi$ 和折扣 $\gamma$ 对应的真实状态值函数一致）时，${\delta }_t^V$ 是一个 $\gamma$－just 优势估计器，并且是 $A^{\pi ,\gamma }$ 的无偏估计器，证明如下：
$$\begin{array}{rl}{\mathbb{E}}_{s_{t+1}}\left[{\delta }_t^{V^{\pi ,\gamma }}\right]& ={\mathbb{E}}_{s_{t+1}}\left[r_t+\gamma V^{\pi ,\gamma }\left(s_{t+1}\right)-V^{\pi ,\gamma }\left(s_t\right)\right]\\ & ={\mathbb{E}}_{s_{t+1}}\left[Q^{\pi ,\gamma }\left(s_t,a_t\right)-V^{\pi ,\gamma }\left(s_t\right)\right]=A^{\pi ,\gamma }\left(s_t,a_t\right).\end{array}$$
接下来，我们考率将$\delta$全部相加，以此估计${\hat{A}}_t^{(k)}$
$$\begin{array}{rl}& \begin{array}{ll}{\hat{A}}_t^{(1)}:={\delta }_t^V& =-V\left(s_t\right)+r_t+\gamma V\left(s_{t+1}\right)\\ {\hat{A}}_t^{(2)}:={\delta }_t^V+\gamma {\delta }_{t+1}^V& =-V\left(s_t\right)+r_t+\gamma r_{t+1}+{\gamma }^{2}V\left(s_{t+2}\right)\\ {\hat{A}}_t^{(3)}:={\delta }_t^V+\gamma {\delta }_{t+1}^V+{\gamma }^2{\delta }_{t+2}^V& =-V\left(s_t\right)+r_t+\gamma r_{t+1}+{\gamma }^2{r}_{t+2}+{\gamma }^{3}V\left(s_{t+3}\right)\end{array}\\ & {\hat{A}}_t^{(k)}:=\sum _{l=0}^{k-1}{\gamma }^l{\delta }_{t+l}^V=-V\left(s_t\right)+r_t+\gamma r_{t+1}+\cdots +{\gamma }^{k-1}{r}_{t+k-1}+{\gamma }^{k}V\left(s_{t+k}\right)\end{array}$$
根据上述式子，我们很容易想到当k趋近于无穷时，有
$${\hat{A}}_t^{(\infty )}=\sum _{l=0}^{\infty }{\gamma }^l{\delta }_{t+l}^V=-V\left(s_t\right)+\sum _{l=0}^{\infty }{\gamma }^l{r}_{t+l}$$
于是我们接下来定义generalized advantage estimator（GAE），如下
$$\begin{array}{rl}{\hat{A}}_t^{\mathrm{GAE}(\gamma ,\lambda )}& :=(1-\lambda )\left({\hat{A}}_t^{(1)}+\lambda {\hat{A}}_t^{(2)}+{\lambda }^2{\hat{A}}_t^{(3)}+\dots \right)\\ & =(1-\lambda )\left({\delta }_t^V+\lambda \left({\delta }_t^V+\gamma {\delta }_{t+1}^V\right)+{\lambda }^2\left({\delta }_t^V+\gamma {\delta }_{t+1}^V+{\gamma }^2{\delta }_{t+2}^V\right)+\dots \right)\\ & =(1-\lambda )({\delta }_t^V\left(1+\lambda +{\lambda }^2+\dots \right)+\gamma {\delta }_{t+1}^V\left(\lambda +{\lambda }^2+{\lambda }^3+\dots \right)\\ & +{\gamma }^2{\delta }_{t+2}^V\left({\lambda }^2+{\lambda }^3+{\lambda }^4+\dots \right)+\dots )\\ & =(1-\lambda )\left({\delta }_t^V\left(\frac{1}{1-\lambda }\right)+\gamma {\delta }_{t+1}^V\left(\frac{\lambda }{1-\lambda }\right)+{\gamma }^2{\delta }_{t+2}^V\left(\frac{{\lambda }^2}{1-\lambda }\right)+\dots \right)\\ & =\sum _{l=0}^{\infty }(\gamma \lambda {)}^l{\delta }_{t+l}^V\end{array}$$
于是，我们定义the discounted policy gradient为
$$g^{\gamma }\approx \mathbb{E}\left[\sum _{t=0}^{\infty }{\nabla }_{\theta }\log {\pi }_{\theta }\left(a_t\mid s_t\right){\hat{A}}_t^{\mathrm{GAE}(\gamma ,\lambda )}\right]=\mathbb{E}\left[\sum _{t=0}^{\infty }{\nabla }_{\theta }\log {\pi }_{\theta }\left(a_t\mid s_t\right)\sum _{l=0}^{\infty }(\gamma \lambda {)}^l{\delta }_{t+l}^V\right]$$
adient为
$$g^{\gamma }\approx \mathbb{E}\left[\sum _{t=0}^{\infty }{\nabla }_{\theta }\log {\pi }_{\theta }\left(a_t\mid s_t\right){\hat{A}}_t^{\mathrm{GAE}(\gamma ,\lambda )}\right]=\mathbb{E}\left[\sum _{t=0}^{\infty }{\nabla }_{\theta }\log {\pi }_{\theta }\left(a_t\mid s_t\right)\sum _{l=0}^{\infty }(\gamma \lambda {)}^l{\delta }_{t+l}^V\right]$$