cs285 lecture9

🔗 GitHub 持续更新仓库（含代码+课件）：
👉 github.com/CalebCheng819/cs285

lecture9

part1

Policy gradient as softened policy iteration

我们可以换一种角度理解策略梯度：将其看作一种“软化版（softened）”的策略迭代（Policy Iteration）。

经典策略迭代结构（policy iteration）：

• Alternating between:
  1. 估计当前策略的值函数 $V^{\pi }$ 或 Advantage；
  2. 使用估计值更新策略（例如贪心选择最优动作）。

类比：

步骤	策略迭代	策略梯度
值估计	准确估计 $A^{\pi }(s,a)$	使用样本/网络近似 Advantage
策略更新	argmax (完全采纳最优动作)	轻微调整策略参数（通过梯度）

策略梯度不会像策略迭代那样直接跳转到贪心策略，而是根据 Advantage 的大小轻微提高动作概率。

这在 Advantage 估计不准时很有用 —— 小步更新可以避免因估计误差而“走错方向”。

理论证明

要证明的结论（最终目标）是：
$$J({\theta }^{\prime })-J(\theta )={\mathbb{E}}_{{\pi }_{{\theta }^{\prime }}}\left[\sum _{t=0}^{\infty }{\gamma }^t{A}^{{\pi }_{\theta }}(s_t,a_t)\right]$$
这一步的目的就是将策略改进的目标函数差值（LHS）转换为新策略分布下旧策略 Advantage 的期望（RHS）。

我们从标准的强化学习目标函数出发：
$$J(\theta )={\mathbb{E}}_{\tau \sim {\pi }_{\theta }}\left[\sum _{t=0}^{\infty }{\gamma }^{t}r(s_t,a_t)\right]$$
我们可以将其改写为：
$$J(\theta )={\mathbb{E}}_{s_0\sim p(s_0)}\left[V^{{\pi }_{\theta }}(s_0)\right]$$
这是因为 Value Function 就是从某状态出发的期望累计奖励。

1. 将 V(s₀) 用 telescoping sum 重写成：

$$V^{{\pi }_{\theta }}(s_0)=\sum _{t=0}^{\infty }{\gamma }^t{V}^{{\pi }_{\theta }}(s_t)-\sum _{t=1}^{\infty }{\gamma }^t{V}^{{\pi }_{\theta }}(s_t)$$

使用下面两个式子：
$$J({\theta }^{\prime })={\mathbb{E}}_{{\pi }_{{\theta }^{\prime }}}\left[\sum _{t=0}^{\infty }{\gamma }^{t}r(s_t,a_t)\right]$$
注意：这两个期望都使用 π′ 的轨迹分布，这是合法的，因为初始状态分布不依赖 θ。

从 lecture 原文中我们看到他写了一个式子：
$$J({\theta }^{\prime })-J(\theta )={\mathbb{E}}_{{\pi }_{{\theta }^{\prime }}}\left[\sum _{t=0}^{\infty }{\gamma }^{t}r(s_t,a_t)+\sum _{t=1}^{\infty }{\gamma }^t{V}^{{\pi }_{\theta }}(s_t)-\sum _{t=0}^{\infty }{\gamma }^t{V}^{{\pi }_{\theta }}(s_t)\right]$$
合并后：
$$={\mathbb{E}}_{{\pi }_{{\theta }^{\prime }}}\left[\sum _{t=0}^{\infty }{\gamma }^t\left(r(s_t,a_t)+\gamma V^{{\pi }_{\theta }}(s_{t+1})-V^{{\pi }_{\theta }}(s_t)\right)\right]$$
这个括号里的表达式，正是 Advantage Function 的定义：
$$A^{{\pi }_{\theta }}(s_t,a_t)=r(s_t,a_t)+\gamma V^{{\pi }_{\theta }}(s_{t+1})-V^{{\pi }_{\theta }}(s_t)$$
所以最终就得到了：
$$J({\theta }^{\prime })-J(\theta )={\mathbb{E}}_{{\pi }_{{\theta }^{\prime }}}\left[\sum _{t=0}^{\infty }{\gamma }^t{A}^{{\pi }_{\theta }}(s_t,a_t)\right]$$
我们希望：

• 用旧策略 π_θ 的数据采样（因为我们还没知道 π_θ’）；
• 那么需要引入 importance sampling 修正权重；

$$\begin{array}{rl}{E}_{\tau \sim p_{{\theta }^{\prime }}(\tau )}\left[\sum _t{\gamma }^t{A}^{{\pi }_{\theta }}\left({\mathbf{s}}_t,{\mathbf{a}}_t\right)\right]& =\sum _t{E}_{{\mathbf{s}}_t\sim p_{{\theta }^{\prime }}\left({\mathbf{s}}_t\right)}\left[E_{{\mathbf{a}}_t\sim {\pi }_{{\theta }^{\prime }}\left({\mathbf{a}}_t\mid {\mathbf{s}}_t\right)}\left[{\gamma }^t{A}^{{\pi }_{\theta }}\left({\mathbf{s}}_t,{\mathbf{a}}_t\right)\right]\right]\\ & =\sum _t{E}_{{\mathbf{s}}_t\sim p_{{\theta }^{\prime }}\left({\mathbf{s}}_t\right)}\left[E_{{\mathbf{a}}_t\sim {\pi }_{\theta }\left({\mathbf{a}}_t\mid {\mathbf{s}}_t\right)}\left[\frac{{\pi }_{{\theta }^{\prime }}\left({\mathbf{a}}_t\mid {\mathbf{s}}_t\right)}{{\pi }_{\theta }\left({\mathbf{a}}_t\mid {\mathbf{s}}_t\right)}{\gamma }^t{A}^{{\pi }_{\theta }}\left({\mathbf{s}}_t,{\mathbf{a}}_t\right)\right]\right]\end{array}$$

我们无法直接从 π_θ’ 采样

• 所以我们希望能近似地用 π_θ 的分布来替代；
• 如果 π_θ 和 π_θ’ 很接近，那么状态分布 d^{π_θ}(s) 和 d^{π_θ’}(s) 也近似；
• 这是 策略迭代的近似前提：改进不能跳太远。

$$\sum _t{E}_{{\mathbf{s}}_t\sim p_{{\theta }^{\prime }}\left({\mathbf{s}}_t\right)}\left[E_{{\mathbf{a}}_t\sim {\pi }_{\theta }\left({\mathbf{a}}_t\mid {\mathbf{s}}_t\right)}\left[\frac{{\pi }_{{\theta }^{\prime }}\left({\mathbf{a}}_t\mid {\mathbf{s}}_t\right)}{{\pi }_{\theta }\left({\mathbf{a}}_t\mid {\mathbf{s}}_t\right)}{\gamma }^t{A}^{{\pi }_{\theta }}\left({\mathbf{s}}_t,{\mathbf{a}}_t\right)\right]\right]\approx \sum _t{E}_{{\mathbf{s}}_t\sim p_{\theta }\left({\mathbf{s}}_t\right)}\left[E_{{\mathbf{a}}_t\sim {\pi }_{\theta }\left({\mathbf{a}}_t\mid {\mathbf{s}}_t\right)}\left[\frac{{\pi }_{{\theta }^{\prime }}\left({\mathbf{a}}_t\mid {\mathbf{s}}_t\right)}{{\pi }_{\theta }\left({\mathbf{a}}_t\mid {\mathbf{s}}_t\right)}{\gamma }^t{A}^{{\pi }_{\theta }}\left({\mathbf{s}}_t,{\mathbf{a}}_t\right)\right]\right]$$

part2

证明$p_{\theta }\left({\mathbf{s}}_t\right)$ is close to $p_{{\theta }^{\prime }}\left({\mathbf{s}}_t\right)$ when ${\pi }_{\theta }$ is close to ${\pi }_{{\theta }^{\prime }}$

假设旧策略 π_θ 是确定性的，即：
$$a_t={\pi }_{\theta }(s_t)$$
若新策略 π_θ′ 在任意状态下以概率 ε 偏离旧策略（即选择不同的动作），则：

• “没出错”的概率为 $(1-ϵ{)}^t$

  这种情况下状态分布与旧策略完全一致：$p_{{\theta }^{\prime }}(s_t)=p_{\theta }(s_t)$

• 剩下的情况则定义为错误分布 $p_{\text{mistake}}(s_t)$，我们对它不做任何假设。

于是有如下表示：
$$p_{{\theta }^{\prime }}(s_t)=(1-ϵ{)}^t{p}_{\theta }(s_t)+\left[1-(1-ϵ{)}^t\right]p_{\text{mistake}}(s_t)$$
该表达式与我们在模仿学习（Behavior Cloning）分析中非常相似。
$$\begin{array}{rl}& \left|p_{{\theta }^{\prime }}\left({\mathbf{s}}_t\right)-p_{\theta }\left({\mathbf{s}}_t\right)\right|=\left(1-(1-ϵ{)}^t\right)\left|p_{\text{mistake }}\left({\mathbf{s}}_t\right)-p_{\theta }\left({\mathbf{s}}_t\right)\right|\le 2\left(1-(1-ϵ{)}^t\right)\le 2ϵt\\ & \text{ useful identity: }(1-ϵ{)}^t\ge 1-ϵt\text{ for }ϵ\in [0,1]\end{array}$$
这意味着：只要 ε 足够小，策略间的微小差异导致的状态分布偏移也会非常小。

接下来分析更加general的情况

引入引理（来自 Trust Region Policy Optimization 论文）：

如果两个分布 π 和 π′ 的 total variation divergence 是 ε，那么存在一个联合分布 $p(x,y)$，使得：

• $p(x)=\pi (x),p(y)={\pi }^{\prime }(y)$
• $P(x=y)=1-ϵ$

${\pi }_{{\theta }^{\prime }}$ is close to ${\pi }_{\theta }$ if $\left|{\pi }_{{\theta }^{\prime }}\left({\mathbf{a}}_t\mid {\mathbf{s}}_t\right)-{\pi }_{\theta }\left({\mathbf{a}}_t\mid {\mathbf{s}}_t\right)\right|\le ϵ$ for all ${\mathbf{s}}_t$

Useful lemma: if $\left|p_X(x)-p_Y(x)\right|=ϵ$, exists $p(x,y)$ such that $p(x)=p_X(x)$ and $p(y)=p_Y(y)$ and $p(x=y)=1-ϵ$ $\Rightarrow p_X(x)$ “agrees” with $p_Y(y)$ with probability $ϵ$
$\Rightarrow {\pi }_{{\theta }^{\prime }}\left({\mathbf{a}}_t\mid {\mathbf{s}}_t\right)$ takes a different action than ${\pi }_{\theta }\left({\mathbf{a}}_t\mid {\mathbf{s}}_t\right)$ with probability at most $ϵ$

所以，我们仍然可以使用之前的分布表示：
$$p_{{\theta }^{\prime }}(s_t)=(1-ϵ{)}^t{p}_{\theta }(s_t)+\left[1-(1-ϵ{)}^t\right]p_{\text{mistake}}(s_t)$$
并同样推导出：
$$\text{TV}(p_{\theta },p_{{\theta }^{\prime }})\le 2ϵt$$

bounding the object value

我们关心的是：
$${\mathbb{E}}_{p_{{\theta }^{\prime }}}\left[f(s_t)\right]-{\mathbb{E}}_{p_{\theta }}\left[f(s_t)\right]$$
可以用以下界限表示：
$$\left|{\mathbb{E}}_{p_{{\theta }^{\prime }}}[f(s)]-{\mathbb{E}}_{p_{\theta }}[f(s)]\right|\le \text{TV}(p_{{\theta }^{\prime }},p_{\theta })\cdot \underset{s}{\max }|f(s)|$$

这是一个泛用技巧，任何两个分布下的期望值差异，都可由最大函数值与全变差距离界定。

于是我们得到：
$$\text{Error Term}\le 2\cdot ϵ\cdot t\cdot C$$
即
$$\begin{array}{rl}& \sum _t{E}_{{\mathbf{s}}_t\sim p_{{\theta }^{\prime }}\left({\mathbf{s}}_t\right)}\left[E_{{\mathbf{a}}_t\sim {\pi }_{\theta }\left({\mathbf{a}}_t\mid {\mathbf{s}}_t\right)}\left[\frac{{\pi }_{{\theta }^{\prime }}\left({\mathbf{a}}_t\mid {\mathbf{s}}_t\right)}{{\pi }_{\theta }\left({\mathbf{a}}_t\mid {\mathbf{s}}_t\right)}{\gamma }^t{A}^{{\pi }_{\theta }}\left({\mathbf{s}}_t,{\mathbf{a}}_t\right)\right]\right]\ge \\ & \sum _t{E}_{{\mathbf{s}}_t\sim p_{\theta }\left({\mathbf{s}}_t\right)}\left[E_{{\mathbf{a}}_t\sim {\pi }_{\theta }\left({\mathbf{a}}_t\mid {\mathbf{s}}_t\right)}\left[\frac{{\pi }_{{\theta }^{\prime }}\left({\mathbf{a}}_t\mid {\mathbf{s}}_t\right)}{{\pi }_{\theta }\left({\mathbf{a}}_t\mid {\mathbf{s}}_t\right)}{\gamma }^t{A}^{{\pi }_{\theta }}\left({\mathbf{s}}_t,{\mathbf{a}}_t\right)\right]\right]-\sum _{t}2ϵtC\end{array}$$
其中 $C=T\cdot R_{\max }$（或 $\frac{R_{\max }}{1-\gamma }$ 若为无限时序）

part3

我们希望：
$$p_{\theta }(s_t)\approx p_{{\theta }^{\prime }}(s_t)\text{当}{\pi }_{\theta }\approx {\pi }_{{\theta }^{\prime }}$$
其中“接近”原先是用 Total Variation Distance (TV distance) 来衡量的。

实践问题：TV Divergence 不易处理

困难点：

• TV 距离涉及绝对值，不易求导；
• 很多连续动作策略无法轻易计算 TV。

解决方案：改用 KL Divergence (相对熵)
$$\begin{array}{rl}& \left|{\pi }_{{\theta }^{\prime }}\left({\mathbf{a}}_t\mid {\mathbf{s}}_t\right)-{\pi }_{\theta }\left({\mathbf{a}}_t\mid {\mathbf{s}}_t\right)\right|\le \sqrt{\frac{1}{2}{D}_{\mathrm{KL}}\left({\pi }_{{\theta }^{\prime }}\left({\mathbf{a}}_t\mid {\mathbf{s}}_t\right)\Vert {\pi }_{\theta }\left({\mathbf{a}}_t\mid {\mathbf{s}}_t\right)\right)}\\ & \Rightarrow D_{\mathrm{KL}}\left({\pi }_{{\theta }^{\prime }}\left({\mathbf{a}}_t\mid {\mathbf{s}}_t\right)\Vert {\pi }_{\theta }\left({\mathbf{a}}_t\mid {\mathbf{s}}_t\right)\right)\text{ bounds state marginal difference }\\ & D_{\mathrm{KL}}\left(p_1(x)\Vert p_2(x)\right)=E_{x\sim p_1(x)}\left[\log \frac{p_1(x)}{p_2(x)}\right]\end{array}$$

实现方式一：拉格朗日乘子法（Lagrangian）

我们将约束问题变为无约束优化：
$$\mathcal{L}\left({\theta }^{\prime },\lambda \right)=\sum _t{E}_{{\mathbf{s}}_t\sim p_{\theta }\left({\mathbf{s}}_t\right)}\left[E_{{\mathbf{a}}_t\sim {\pi }_{\theta }\left({\mathbf{a}}_t\mid {\mathbf{s}}_t\right)}\left[\frac{{\pi }_{{\theta }^{\prime }}\left({\mathbf{a}}_t\mid {\mathbf{s}}_t\right)}{{\pi }_{\theta }\left({\mathbf{a}}_t\mid {\mathbf{s}}_t\right)}{\gamma }^t{A}^{{\pi }_{\theta }}\left({\mathbf{s}}_t,{\mathbf{a}}_t\right)\right]\right]-\lambda \left(D_{\mathrm{KL}}\left({\pi }_{{\theta }^{\prime }}\left({\mathbf{a}}_t\mid {\mathbf{s}}_t\right)\Vert {\pi }_{\theta }\left({\mathbf{a}}_t\mid {\mathbf{s}}_t\right)\right)-ϵ\right)$$

• 当 KL > ε，λ ↑ 来加强惩罚；
• 当 KL < ε，λ ↓ 放松惩罚。

算法步骤：Dual Gradient Descent

1. 固定 λ，优化 θ′（梯度上升）；
2. 固定 θ′，更新 λ（梯度下降）：

$$\lambda \leftarrow \lambda +\eta (\text{KL}-ϵ)$$

这种方式能收敛到满足约束的最优策略参数 θ′

实现方式二：正则化处理（Regularization）

一种更简单但经验有效的做法：
$$\underset{{\theta }^{\prime }}{\max }{\mathbb{E}}_{s,a}[\hat{A}(s,a)]-\lambda \cdot \text{KL}({\pi }_{{\theta }^{\prime }}||{\pi }_{\theta })$$

• 不设置严格约束；
• 将 KL 作为一个 soft penalty；
• λ 可以人为设定（调参）或动态调整。

在 PPO（Proximal Policy Optimization）和 Guided Policy Search 中就采用了这种方式。

part4——Natural Policy Gradient（自然策略梯度）

目标：
$$\underset{{\theta }^{\prime }}{\max }{\mathbb{E}}_{s\sim p_{\theta }(s)}\left[\sum _a{\pi }_{{\theta }^{\prime }}(a|s)A^{{\pi }_{\theta }}(s,a)\right]\text{s.t.}\text{KL}({\pi }_{{\theta }^{\prime }}||{\pi }_{\theta })\le ϵ$$
上一节中，我们通过拉格朗日方法或正则项实现了此约束。

使用一阶泰勒展开（First-Order Taylor Expansion）

我们将目标函数 $J({\theta }^{\prime })$ 在 θ 附近做线性化（taylor approximation）：
$$J({\theta }^{\prime })\approx J(\theta )+{\nabla }_{\theta }J(\theta {)}^T({\theta }^{\prime }-\theta )$$
即：我们只保留线性项，优化这个线性函数。

这时必须引入“信赖域”约束，避免优化发散（如往无穷大方向走）。

图示直觉（Trust Region）

• 蓝色曲线：真实目标函数
• 绿色线：一阶泰勒近似
• 红框区域：我们信赖的一小块“近似还算准确”的空间（trust region）

我们在红框中优化绿色线（近似函数），来替代优化真实目标。

回想到一般的梯度上升做法类似于此，相当于解下面的约束优化问题：
$${\theta }^{\prime }\leftarrow \arg \underset{{\theta }^{\prime }}{\max }{\nabla }_{\theta }J(\theta {)}^T({\theta }^{\prime }-\theta )\text{s.t.}\Vert {\theta }^{\prime }-\theta {\Vert }^2\le ϵ$$
这是在参数空间中以欧几里得距离为约束的最优化 —— 实质就是：

普通梯度上升是在「参数空间」的圆形信赖域里找最优点。

有封闭解（公式给出）：
$${\theta }^{\prime }=\theta +\sqrt{\frac{ϵ}{\Vert {\nabla }_{\theta }J(\theta ){\Vert }^2}}{\nabla }_{\theta }J(\theta )$$

• 方向是梯度方向；
• 步长大小由 epsilon 和梯度范数共同决定。

问题在于：这个圆在参数空间中是对称的，但我们真正关心的是策略分布（而不是参数本身）有没有大改动，所以这个圆有可能约束错了方向。

于是我们对 KL divergence 做二阶近似：
$$\text{KL}({\pi }_{{\theta }^{\prime }}||{\pi }_{\theta })\approx \frac{1}{2}({\theta }^{\prime }-\theta {)}^{T}F({\theta }^{\prime }-\theta )$$
其中 F 是 Fisher Information Matrix（Fisher 信息矩阵）：
$$F={\mathbb{E}}_{s\sim p_{\theta },a\sim {\pi }_{\theta }}\left[{\nabla }_{\theta }\log {\pi }_{\theta }(a|s){\nabla }_{\theta }\log {\pi }_{\theta }(a|s{)}^T\right]$$
它描述了：改变 θ 时，对动作分布 π(a|s) 有多大影响。

求解这个二次约束的线性优化问题，结果为：
$${\theta }^{\prime }=\theta +\alpha F^{-1}{\nabla }_{\theta }J(\theta )$$

$$\alpha =\sqrt{\frac{2ϵ}{{\nabla }_{\theta }J(\theta {)}^T\mathbf{F}{\nabla }_{\theta }J(\theta )}}$$

这就是 Natural Policy Gradient：

Natural Gradient = Fisher 信息矩阵的逆 × 普通梯度

它自动对不同参数的“灵敏度”做了调整，解决了普通梯度更新中 step size 不一致、方向不合理的问题。

方法	约束空间	对灵敏度的处理
普通 Policy Gradient	参数空间中的欧氏球体	忽略各参数对概率的影响差异
Natural Policy Gradient	分布空间中的 KL 椭球体	用 F 处理非均匀灵敏度

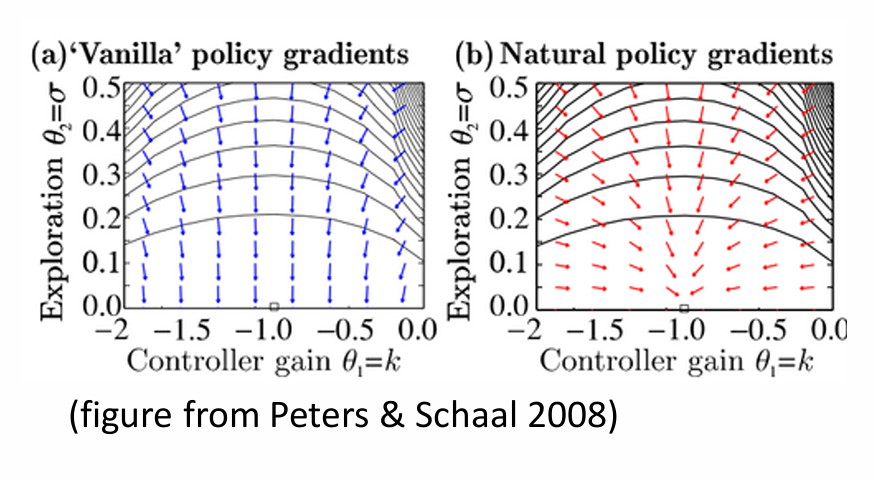
难点在于 ${\mathbf{F}}^{-1}\nabla J$ 的计算，不能直接求 $F$ 的逆，因为它是一个大矩阵；

-------------------- | ---------------------- | -------------------------- |
| 普通 Policy Gradient | 参数空间中的欧氏球体 | 忽略各参数对概率的影响差异 |
| Natural Policy Gradient | 分布空间中的 KL 椭球体 | 用 F 处理非均匀灵敏度 |

[外链图片转存中…(img-faYLDJqj-1753520265927)]

难点在于 ${\mathbf{F}}^{-1}\nabla J$ 的计算，不能直接求 $F$ 的逆，因为它是一个大矩阵；

实际中使用 Fisher-vector product + 共轭梯度法（Conjugate Gradient） 来逼近。