cs285 hw2

最新推荐文章于 2026-01-08 22:28:34 发布

原创最新推荐文章于 2026-01-08 22:28:34 发布 · 1k 阅读

20 ·

CC 4.0 BY-SA版权

文章标签：

#算法 #机器学习 #人工智能 #深度学习

cs285 专栏收录该内容

12 篇文章

订阅专栏

hw2

review

variance reduction

reward to go

为了减少式子中的causality，我们使用t到T-1的reward
$\nabla_\theta J(\theta) \approx \frac{1}{N} \sum_{i=1}^N \sum_{t=0}^{T-1} \nabla_\theta \log \pi_\theta\left(a_{i t} \mid s_{i t}\right)\left(\sum_{t^{\prime}=t}^{T-1} r\left(s_{i t^{\prime}}, a_{i t^{\prime}}\right)\right)$

discounting

我们有两种方式，一种是一种是把discount加到full trajectory
$\nabla_\theta J(\theta) \approx \frac{1}{N} \sum_{i=1}^N\left(\sum_{t=0}^{T-1} \nabla_\theta \log \pi_\theta\left(a_{i t} \mid s_{i t}\right)\right)\left(\sum_{t^{\prime}=0}^{T-1} \gamma^{t^{\prime}-1} r\left(s_{i t^{\prime}}, a_{i t^{\prime}}\right)\right)$
另一种是把discount加到reward to go（推荐）
$\nabla_\theta J(\theta) \approx \frac{1}{N} \sum_{i=1}^N \sum_{t=0}^{T-1} \nabla_\theta \log \pi_\theta\left(a_{i t} \mid s_{i t}\right)\left(\sum_{t^{\prime}=t}^{T-1} \gamma^{t^{\prime}-t} r\left(s_{i t^{\prime}}, a_{i t^{\prime}}\right)\right)$

baseline

我们考虑用一个state-independent（unbiased）的value function作为baseline
$V_\phi^\pi\left(s_t\right) \approx \sum_{t^{\prime}=t}^{T-1} \mathbb{E}_{\pi_\theta}\left[r\left(s_{t^{\prime}}, a_{t^{\prime}}\right) \mid s_t\right]$

$\nabla_\theta J(\theta) \approx \frac{1}{N} \sum_{i=1}^N \sum_{t=0}^{T-1} \nabla_\theta \log \pi_\theta\left(a_{i t} \mid s_{i t}\right)\left(\left(\sum_{t^{\prime}=t}^{T-1} \gamma^{t^{\prime}-t} r\left(s_{i t^{\prime}}, a_{i t^{\prime}}\right)\right)-V_\phi^\pi\left(s_{i t}\right)\right)$

GAE

我们可以把advantage function这么表示
$A^\pi\left(s_t, a_t\right)=Q^\pi\left(s_t, a_t\right)-V^\pi\left(s_t\right)$
其中Q是通过Monte Carlo估计的，V是通过已经学习到的 $VϕπV_\phi^\pi$ 。我们可以进一步降低方差利用 $VϕπV_\phi^\pi$ 去替代Monte Carlo估计的Q。于是得到
$A^\pi\left(s_t, a_t\right) \approx \delta_t=r\left(s_t, a_t\right)+\gamma V_\phi^\pi\left(s_{t+1}\right)-V_\phi^\pi\left(s_t\right)$
但是这样子会因为 $VϕπV_\phi^\pi$ 错误的modeling而引入新的bias，于是我么可以考虑引入n-step
$A_n^\pi\left(s_t, a_t\right)=\sum_{t^{\prime}=t}^{t+n} \gamma^{t^{\prime}-t} r\left(s_{t^{\prime}}, a_{t^{\prime}}\right)+\gamma^n V_\phi^\pi\left(s_{t+n+1}\right)-V_\phi^\pi\left(s_t\right)$
接下来，我们引入 $λ\lambda$ 引入指数加权，其中 $λ\lambda$ 属于[0,1]
$A_{G A E}^\pi\left(s_t, a_t\right)=\frac{1-\lambda^{T-t-1}}{1-\lambda} \sum_{n=1}^{T-t-1} \lambda^{n-1} A_n^\pi\left(s_t, a_t\right)$
注意求和上限是T-t-1，当T趋近于无穷时，有
$\begin{aligned} A_{G A E}^\pi\left(s_t, a_t\right) & =\frac{1}{1-\lambda} \sum_{n=1}^{\infty} \lambda^{n-1} A_n^\pi\left(s_t, a_t\right) \\ & =\sum_{t^{\prime}=t}^{\infty}(\gamma \lambda)^{t^{\prime}-t} \delta_{t^{\prime}} \end{aligned}$
最后，我们对finite的情况化简一下
$A_{G A E}^\pi\left(s_t, a_t\right)=\sum_{t^{\prime}=t}^{T-1}(\gamma \lambda)^{t^{\prime}-t} \delta_{t^{\prime}}$
于是，接下来我们可以用递归形式（便与写代码）
$A_{G A E}^\pi\left(s_t, a_t\right)=\delta_t+\gamma \lambda A_{G A E}^\pi\left(s_{t+1}, a_{t+1}\right)$

code

在配置环境前，会出现

  note: This error originates from a subprocess, and is likely not a problem with pip.
  ERROR: Failed building wheel for box2d-py
  Running setup.py clean for box2d-py
Failed to build box2d-py
ERROR: Failed to build installable wheels for some pyproject.toml based projects (box2d-py)

后尝试先pip install swig后再pip install -r requirements.txt成功解决

在进行编译的时候还出现了

RuntimeError: module compiled against ABI version 0x1000009 but this version of numpy is 0x2000000                                                                                          
RuntimeError: module compiled against ABI version 0x1000009 but this version of numpy is 0x2000000                                                                                          
Traceback (most recent call last):
  File "/home/robot/cjt_cs/cs285/cs285/code/homework_fall2023/hw2/cs285/scripts/run_hw2.py", line 14, in <module>
    from cs285.infrastructure import utils
  File "/home/robot/cjt_cs/cs285/cs285/code/homework_fall2023/hw2/cs285/infrastructure/utils.py", line 6, in <module>
    import cv2
ImportError: numpy.core.multiarray failed to import

后先手动删除旧版本pip uninstall numpy opencv-python opencv-python-headless -y,再重新安装目前最稳定的兼容版本pip install numpy==1.24.4 opencv-python==4.7.0.72得以解决

当然在安装环境依赖的时候，也可以考虑使用清华镜像源pip install -r requirements.txt -i https://pypi.tuna.tsinghua.edu.cn/simple

networks

policies.py

在MLPPolicy中我们应该写forward和get_action这些函数，update应该更新到子类中，因为不同的policy会有不同的算法

_distribution

定义了如何根据输入的观测（observation）生成一个概率分布，用于从中采样动作。

    def _distribution(self, obs: torch.FloatTensor) -> distributions.Distribution:
        """Returns a distribution over actions given an observation."""
        if self.discrete:
            logits = self.logits_net(obs)
            return distributions.Categorical(logits=logits)
        else:
            mean = self.mean_net(obs)
            std = torch.exp(self.logstd)
            return distributions.Normal(mean, std)

如果环境的动作是离散的（例如：上下左右，0/1等），我们通常使用 Categorical 分布。

self.logits_net 是一个神经网络，它接受观测 obs 并输出每个可能动作的logits（未归一化的对数概率）。
如果动作是连续的（例如：力的大小、角度等），我们使用正态分布 Normal。

self.mean_net: 神经网络，输入观测 obs，输出每个动作维度的均值。

self.logstd: 是一个可学习的张量，表示对数标准差（log std），通过 exp 还原出标准差。

update

   def update(
        self,
        obs: np.ndarray,
        actions: np.ndarray,
        advantages: np.ndarray,
    ) -> dict:
        """Implements the policy gradient actor update."""
        obs = ptu.from_numpy(obs)
        actions = ptu.from_numpy(actions)
        advantages = ptu.from_numpy(advantages)

        # TODO: implement the policy gradient actor update.
        self.optimizer.zero_grad()
        dist=self(obs)
        logp=dist.log_prob(actions)#dist的性质计算对数概率
        if logp.dim()>1:
            logp=logp.sum(-1)
        loss=-(logp*advantages).sum()#含有advantage不建议mean
        loss.backward()
        self.optimizer.step()
        return {
            "Actor Loss": ptu.to_numpy(loss),
        }

update() 是每一步 actor 更新的过程，每一次更新都需要执行：

清空上一次的梯度（zero_grad()）；
计算新一批数据的 loss（基于当前 obs, actions, advantages）；
反向传播新 loss 的梯度；
更新网络参数（step）

其中因为 MLPPolicyPG 继承自 MLPPolicy，而 MLPPolicy 又继承自 nn.Module，这是 PyTorch 的神经网络模块的基类。在 nn.Module 中，已经实现了：

pythonCopyEditdef __call__(self, *input, **kwargs):
    return self.forward(*input, **kwargs)

也就是说，当你调用 self(obs) 时，其实内部就是在调用 self.forward(obs)。

critics.py

forward

给定一个 batch 的 observation obs，返回网络预测的 $V (s)$ 值。

    def forward(self, obs: torch.Tensor) -> torch.Tensor:#
        # TODO: implement the forward pass of the critic network
        return self.network(obs).squeeze(-1)  # Remove the last dimension
        # This should return a tensor of shape (batch_size,) where each element corresponds to the
        # value of the observation in the batch.
        # If you want to keep the output as a 2D tensor with shape (batch_size, 1), you can remove the .squeeze(-1) part.

注意 squeeze(-1) 是把形状 (batch_size, 1) 转成 (batch_size,)，以匹配后续计算。

update

    def update(self, obs: np.ndarray, q_values: np.ndarray) -> dict:
        obs = ptu.from_numpy(obs)
        q_values = ptu.from_numpy(q_values)

        # TODO: update the critic using the observations and q_values
        self.optimizer.zero_grad()
        predictions = self(obs)
        loss = F.mse_loss(predictions, q_values)
        loss.backward()
        self.optimizer.step()
        # The loss is the mean squared error between the predicted values and the target q_values.
        # The target q_values are the expected returns for the given observations.
        return {
            "Baseline Loss": ptu.to_numpy(loss),
        }

loss计算也可以通过loss = torch.square(self(obs) - q_values).mean()但更加推荐F.mse_loss(predictions, q_values)这个方法

agents

pg_agent

_calculate_q_vals

计算动作价值函数，关键特性：

同时依赖状态和动作
包含即时奖励

    def _calculate_q_vals(self, rewards: Sequence[np.ndarray]) -> Sequence[np.ndarray]:#Q相对于V多包含了一个即使奖励，返回的是一个列表
        """Monte Carlo estimation of the Q function."""

        if not self.use_reward_to_go:
            # Case 1: in trajectory-based PG, we ignore the timestep and instead use the discounted return for the entire
            # trajectory at each point.
            # In other words: Q(s_t, a_t) = sum_{t'=0}^T gamma^t' r_{t'}
            # TODO: use the helper function self._discounted_return to calculate the Q-values
            q_values = [np.array(self._discounted_return(r),dtype=np.float32) for r in rewards]
        else:
            # Case 2: in reward-to-go PG, we only use the rewards after timestep t to estimate the Q-value for (s_t, a_t).
            # In other words: Q(s_t, a_t) = sum_{t'=t}^T gamma^(t'-t) * r_{t'}
            # TODO: use the helper function self._discounted_reward_to_go to calculate the Q-values
            q_values = [np.array(self._discounted_reward_to_go(r),dtype=np.float32) for r in rewards]
        return q_values

额外引入一个_calculate_q_vals便于将多条轨迹的rewards拆分后处理
对于q_values = [np.array(self._discounted_return(r),dtype=np.float32) for r in rewards]:

假设你收集了一批 n 条 trajectory，每条 trajectory 是一个长度为 T_i 的 reward 序列 r_i，我们想对每条都计算它的 discounted return

_discounted_return

$\text { Return }=\sum_{t^{\prime}=0}^T \gamma^{t^{\prime}} r_{t^{\prime}}$

返回一个具有相同total_return的列表

    def _discounted_return(self, rewards: Sequence[float]) -> Sequence[float]:
        """
        Helper function which takes a list of rewards {r_0, r_1, ..., r_t', ... r_T} and returns
        a list where each index t contains sum_{t'=0}^T gamma^t' r_{t'}

        Note that all entries of the output list should be the exact same because each sum is from 0 to T (and doesn't
        involve t)!
        """
        total_return = 0.0
        for t, r in enumerate(rewards):
            total_return += self.gamma ** t * r
        return [total_return] * len(rewards)  # Return the same value for each
        # index, since the return is the same for all timesteps in the trajectory.
        # This is because the return is calculated from the start of the trajectory to the end,
        # and does not depend on the specific timestep t.

for t, r in ...：将每一对 (index, value) 解包为 t（时间步索引）和 r（该时间步的奖励值）。

_discounted_reward_to_go

$Q\left(s_t, a_t\right)=\sum_{t^{\prime}=t}^T \gamma^{t^{\prime}-t} \cdot r_{t^{\prime}}$

计算每一个时间步 t 对应的 Reward-to-Go 值，也就是从当前时间步开始，到轨迹终止为止的累计折扣回报，返回的是一个具有不同值的列表

    def _discounted_reward_to_go(self, rewards: Sequence[float]) -> Sequence[float]:
        """
        Helper function which takes a list of rewards {r_0, r_1, ..., r_t', ... r_T} and returns a list where the entry
        in each index t' is sum_{t'=t}^T gamma^(t'-t) * r_{t'}.
        """
        # batch_size = len(rewards)
        # q_values = np.zeros(batch_size)
        # for t in range(batch_size):
        #     for t_prime in range(t, batch_size):
        #         q_values[t] += (self.gamma ** (t_prime - t)) * rewards[t_prime]
        # return q_values
        returns,current_return = [], 0.0
        for r in reversed(rewards):
            current_return = r + self.gamma * current_return
            returns.append(current_return)
        returns.reverse()
        return returns
        # This function calculates the discounted reward-to-go for each timestep in the trajectory.
        # It starts from the end of the trajectory and works backwards, accumulating the rewards while applying
        # the discount factor. The result is a list where each entry corresponds to the total discounted
        # reward from that timestep to the end of the trajectory.

在原始方式中，回报 $G_t$ 是从当前时间步 $t$ 开始，到episode结束所有奖励的加权和：
$G_t = r_t + \gamma r_{t+1} + \gamma^2 r_{t+2} + \dots + \gamma^{T-t} r_T$
这会导致一个嵌套循环。为了优化，可以使用 向后累加（reverse accumulation） 的单循环版本。

_estimate_advantage

策略梯度的目标是用：
$\nabla_\theta \log \pi_\theta(a_t | s_t) \cdot A_t$
其中 $A_t = Q(s_t, a_t) - V(s_t)$

    def _estimate_advantage(
        self,
        obs: np.ndarray,
        rewards: np.ndarray,
        q_values: np.ndarray,
        terminals: np.ndarray,
    ) -> np.ndarray:
        """Computes advantages by (possibly) subtracting a value baseline from the estimated Q-values.

        Operates on flat 1D NumPy arrays.
        """ 

        if self.critic is None:
            # TODO: if no baseline, then what are the advantages?
            advantages = q_values
        else:
            # TODO: run the critic and use it as a baseline
            with torch.no_grad():
                obs_tensor = ptu.from_numpy(obs)
                values = self.critic(obs_tensor).cpu().numpy()
            
            assert values.shape == q_values.shape

            if self.gae_lambda is None:
                # TODO: if using a baseline, but not GAE, what are the advantages?
                advantages = q_values - values
            else:
                # TODO: implement GAE
                batch_size = obs.shape[0]

                # HINT: append a dummy T+1 value for simpler recursive calculation,方便递归
                values = np.append(values, [0])
                advantages = np.zeros(batch_size + 1)
                
                for i in reversed(range(batch_size)):
                    # TODO: recursively compute advantage estimates starting from timestep T.
                    # HINT: use terminals to handle edge cases. terminals[i] is 1 if the state is the last in its
                    # trajectory, and 0 otherwise.
                    delta = rewards[i] + self.gamma * values[i + 1] * (1 - terminals[i]) - values[i]#在计算value函数时，考虑了gamma和终止状态
                    advantages[i] = delta + self.gamma * self.gae_lambda * advantages[i + 1] * (1 - terminals[i])#往回递归在外面加一个dummy

                # remove dummy advantage
                advantages = advantages[:-1]

        # TODO: normalize the advantages to have a mean of zero and a standard deviation of one within the batch
        if self.normalize_advantages:
            advantages = (advantages - np.mean(advantages)) / (np.std(advantages) + 1e-8)
        # This normalization helps stabilize training by ensuring that the advantages have a consistent scale.
        # It prevents large advantages from disproportionately influencing the policy updates, which can lead to
        # instability in the learning process.

        return advantages

如果没有 baseline（即 critic），那就用 $A_t = Q(s_t, a_t)$
有 baseline，可以减少方差，用 $A_t = Q(s_t, a_t) - V(s_t)$ ，在计算value的时候，记得with torch.no_grad():
terminals 就是一个布尔列表：

每一个元素 terminals[t] 表示第 t 步是否为终止状态（True 表示终止，False 表示还在进行中）；

如果你使用如 OpenAI Gym 或 CS285 框架，terminals 通常是由 env.step() 的 done 字段得到的。
delta（TD error） 是：
$\delta_t = r_t + \gamma V(s_{t+1}) - V(s_t)$
如果 terminals[i] == 1（即 episode 结束），那么 $δt=rt−V(st)\delta_t = r_t - V(s_t)$ 。
append dummy 值为了在循环中方便地处理 $V(s_{t+1})$ ，防止越界。
归一化 (normalize_advantages)：
- 这一步是为了提升训练稳定性。
- 处理后的 advantage 有零均值和单位标准差，有助于减小梯度爆炸/消失的风险。

update

整个函数的流程图

采样的多个 trajectory
   └── obs, actions, rewards, terminals
        └──➡ _calculate_q_vals(rewards)
              └── q_values (list)
        └──➡ flatten 成 batch
              └── obs, actions, q_values, rewards, terminals
        └──➡ _estimate_advantage()
              └── advantages
        └──➡ actor.update()
              └── info dict
        └──(optional) critic.update()
              └── 更新 info dict

    def update(
        self,
        obs: Sequence[np.ndarray],
        actions: Sequence[np.ndarray],
        rewards: Sequence[np.ndarray],
        terminals: Sequence[np.ndarray],
    ) -> dict:
        """The train step for PG involves updating its actor using the given observations/actions and the calculated
        qvals/advantages that come from the seen rewards.

        Each input is a list of NumPy arrays, where each array corresponds to a single trajectory. The batch size is the
        total number of samples across all trajectories (i.e. the sum of the lengths of all the arrays).
        """
        # obs = np.concatenate(obs, axis=0)  # shape (batch_size, ob_dim)
        # actions = np.concatenate(actions, axis=0)  # shape (batch_size, ac_dim)
        
        # terminals = np.concatenate(terminals, axis=0)  # shape (batch_size,
        # step 1: calculate Q values of each (s_t, a_t) point, using rewards (r_0, ..., r_t, ..., r_T)
        q_values: Sequence[np.ndarray] = self._calculate_q_vals(rewards)
        # q_values should be a list of NumPy arrays, where each array corresponds to a single trajectory.
        # this line flattens it into a single NumPy array.
        # q_values = np.concatenate(q_values, axis=0)  # shape (batch_size,)
        # TODO: flatten the lists of arrays into single arrays, so that the rest of the code can be written in a vectorized
        # way. obs, actions, rewards, terminals, and q_values should all be arrays with a leading dimension of `batch_size`
        # beyond this point.
        obs = self.safe_concatenate("obs", obs)  # shape (batch_size, ob_dim)
        actions = self.safe_concatenate("actions", actions)  # shape (batch_size, ac_dim)
        rewards = self.safe_concatenate("rewards", rewards)  # shape (batch_size,)
        q_values = self.safe_concatenate("q_values", q_values)  # shape (batch_size,)
        terminals = self.safe_concatenate("terminals", terminals)  # shape (batch_size,) 
        # step 2: calculate advantages from Q values
        advantages: np.ndarray = self._estimate_advantage(
            obs, rewards, q_values, terminals
        )
       
        # step 3: use all datapoints (s_t, a_t, adv_t) to update the PG actor/policy
        # TODO: update the PG actor/policy network once using the advantages
        info: dict = self.actor.update(obs, actions, advantages)

        # step 4: if needed, use all datapoints (s_t, a_t, q_t) to update the PG critic/baseline
        if self.critic is not None:
            
            # TODO: perform `self.baseline_gradient_steps` updates to the critic/baseline network
            for _ in range(self.baseline_gradient_steps):
                critic_info: dict = self.critic.update(obs, q_values)
                # critic_info should contain the loss and any other metrics you want to log.
                # You can use critic_info to log the critic's performance.
                info.update(critic_info)    
            # critic_info should contain the loss and any other metrics you want to log.
            # You can use critic_info to log the critic's performance.

            

        return info

首先计算q值，在计算q值的时候，rewards是一个含有多条轨迹的列表
然后把这些数据“打平”为一个批次（batch_size = 所有时间步总和），才能做向量化训练。

因为_estimate_advantage传入的参数是已经被打平的numpy，所以在计算advantage前需要展平

def _estimate_advantage(
        self,
        obs: np.ndarray,
        rewards: np.ndarray,
        q_values: np.ndarray,
        terminals: np.ndarray,
    ) -> np.ndarray:

如果使用了基线（baseline），就要训练一个 critic 网络去拟合 q_values。

执行若干次 critic 更新，并将 critic 的日志信息更新到 info 中。

scripts

run_hw2.py

run_training_loop

    # add action noise, if needed
    if args.action_noise_std > 0:
        assert not discrete, f"Cannot use --action_noise_std for discrete environment {args.env_name}"
        env = ActionNoiseWrapper(env, args.seed, args.action_noise_std)

在连续动作空间的环境中，添加动作噪声（action noise）以增强策略探索能力。

    for itr in range(args.n_iter):
        print(f"\n********** Iteration {itr} ************")
        # TODO: sample `args.batch_size` transitions using utils.sample_trajectories
        # make sure to use `max_ep_len`
        trajs, envsteps_this_batch = utils.sample_trajectories(env,agent.actor,args.batch_size,max_ep_len)  # TODO
        total_envsteps += envsteps_this_batch

在这里面的sample_trajectories，参数应该是agent.actor和args.batch_size
- 在 CS285 框架中，一个 agent 往往是一个类（比如 PGAgent），里面包含了多个模块，例如：
```
pythonCopyEditclass PGAgent:
    def __init__(self):
        self.actor = MLPPolicy(...)
        self.replay_buffer = ...
        self.critic = ...
```
  其中，actor 是负责给定状态 $s$ 产生动作 $a$ 的策略（policy），是我们真正要在环境中 roll out 的“智能体”。
  
  所以，agent.actor 表示从这个 agent 里 拿出策略网络（policy），用于采样轨迹（trajectory）。
- args.batch_size 在 CS285 的代码框架中，实际上是表示“每个策略更新批次中总共收集多少个时间步（timesteps）”，而不是传统意义上神经网络中的“样本个数”的 batch size。

        trajs_dict = {k: [traj[k] for traj in trajs] for k in trajs[0]}

        # TODO: train the agent using the sampled trajectories and the agent's update function
        train_info: dict = agent.update(
            obs=trajs_dict["observation"],
            actions=trajs_dict["action"],
            rewards=trajs_dict["reward"],
            terminals=trajs_dict["terminal"],
        )

外层字典推导式：{k: ... for k in trajs[0]}
- 遍历第一个 trajectory 的所有键（如 'observation', 'action', 'reward'）
- 也就是说：对于每种 key，我们要收集所有轨迹中的对应值
内层列表推导式：[traj[k] for traj in trajs]
- 对于每一条轨迹 traj，提取当前 key（例如 'reward'）对应的值
- 最终生成一个列表：这个 key 在所有 trajectory 中的值的集合

experiments

reward to go&&normalize_advantages

python cs285/scripts/run_hw2.py --env_name CartPole-v0 -n 100 -b 1000 \
--exp_name cartpole
python cs285/scripts/run_hw2.py --env_name CartPole-v0 -n 100 -b 1000 \
-rtg --exp_name cartpole_rtg
python cs285/scripts/run_hw2.py --env_name CartPole-v0 -n 100 -b 1000 \
-na --exp_name cartpole_na
python cs285/scripts/run_hw2.py --env_name CartPole-v0 -n 100 -b 1000 \
-rtg -na --exp_name cartpole_rtg_na
python cs285/scripts/run_hw2.py --env_name CartPole-v0 -n 100 -b 4000 \
--exp_name cartpole_lb
python cs285/scripts/run_hw2.py --env_name CartPole-v0 -n 100 -b 4000 \
-rtg --exp_name cartpole_lb_rtg
python cs285/scripts/run_hw2.py --env_name CartPole-v0 -n 100 -b 4000 \
-na --exp_name cartpole_lb_na
python cs285/scripts/run_hw2.py --env_name CartPole-v0 -n 100 -b 4000 \
-rtg -na --exp_name cartpole_lb_rtg_na

相应文件位置：

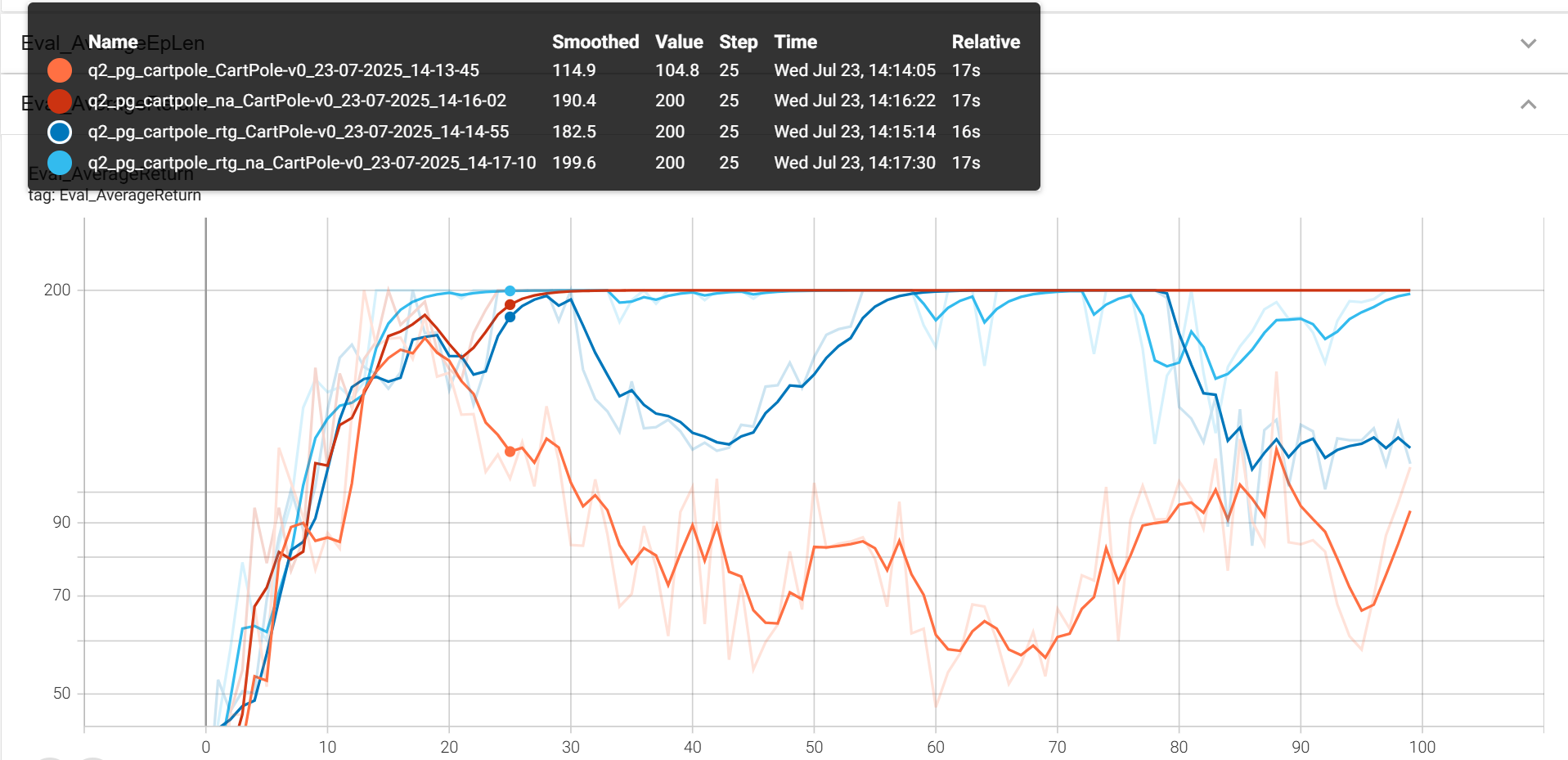
小batch_size:

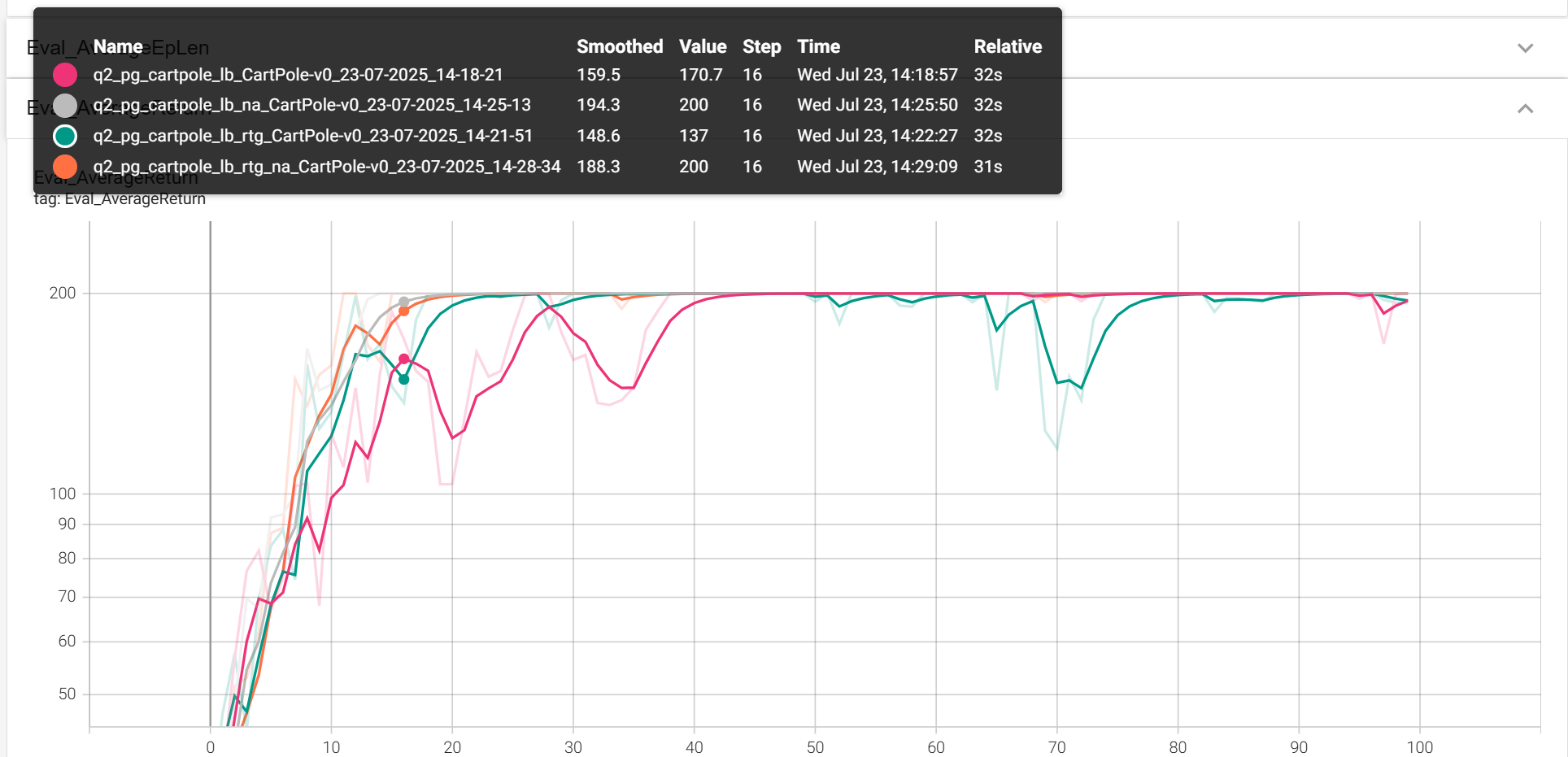
大batch_size

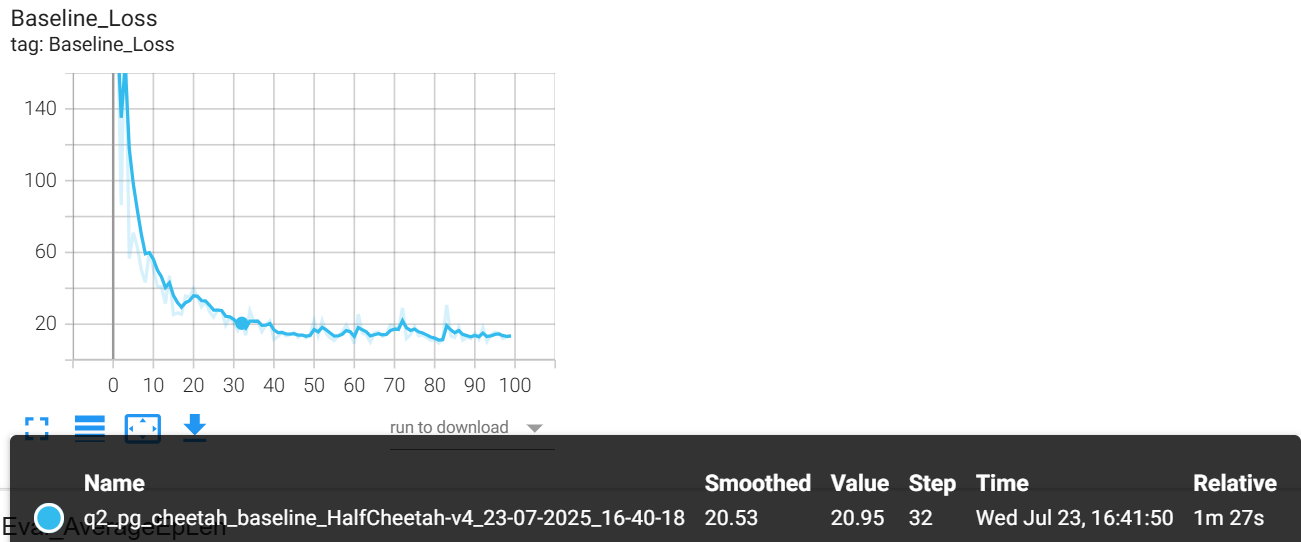
baseline

# No baseline
python cs285/scripts/run_hw2.py --env_name HalfCheetah-v4 \
-n 100 -b 5000 -rtg --discount 0.95 -lr 0.01 \
--exp_name cheetah
# Baseline
python cs285/scripts/run_hw2.py --env_name HalfCheetah-v4 \
-n 100 -b 5000 -rtg --discount 0.95 -lr 0.01 \
--use_baseline -blr 0.01 -bgs 5 --exp_name cheetah_baseline

文件存储位置

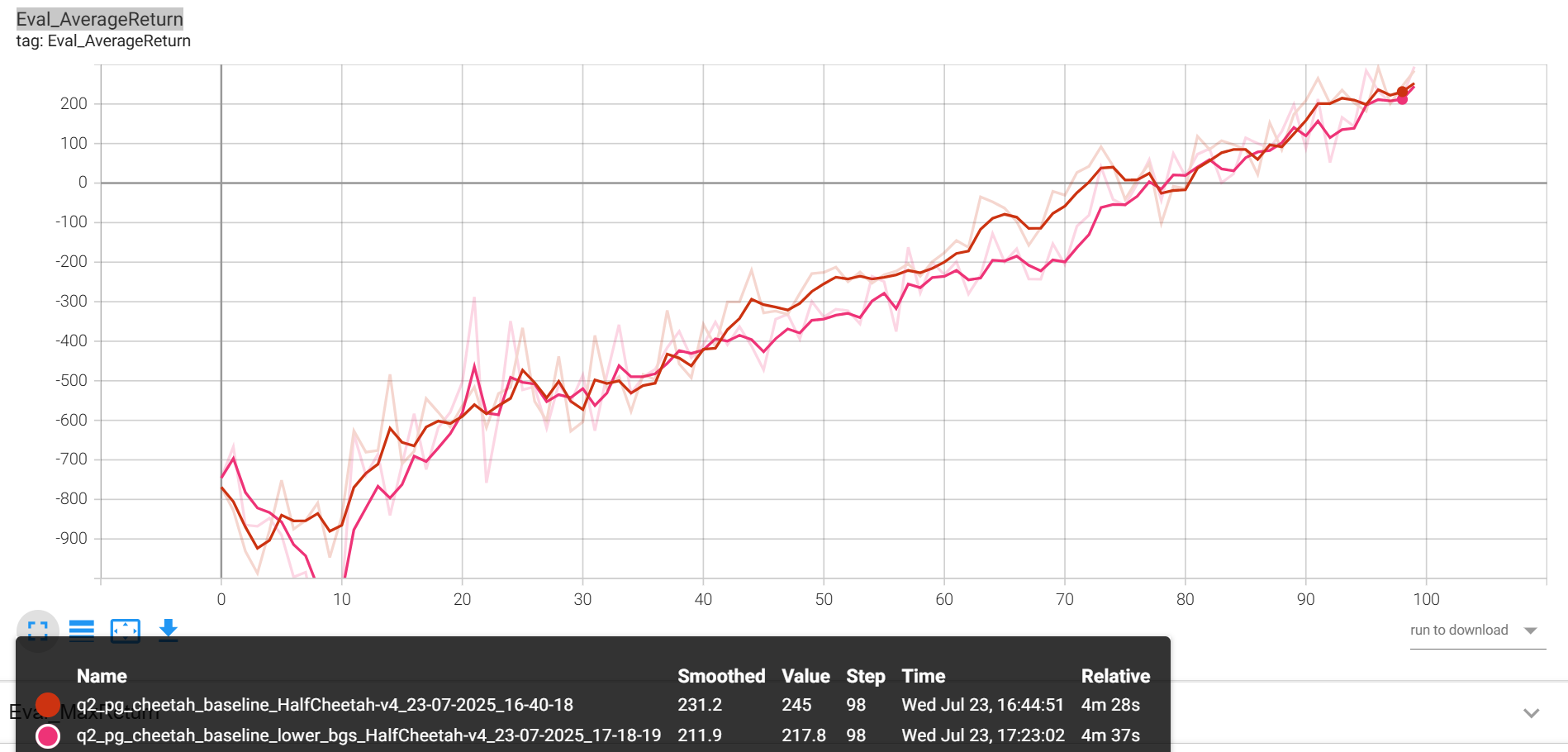
baseline loss

Eval_AverageReturn

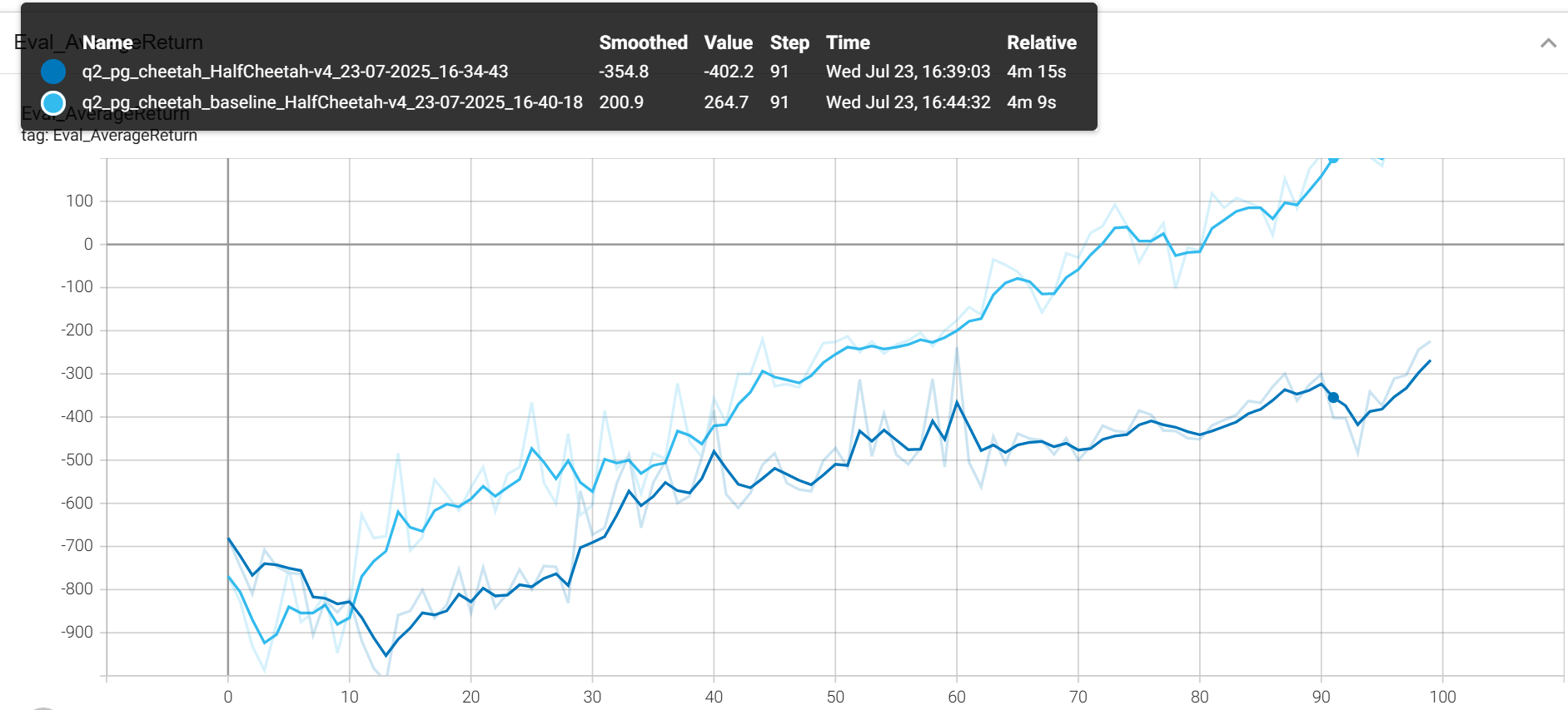
更小的blr

python cs285/scripts/run_hw2.py --env_name HalfCheetah-v4 \
-n 100 -b 5000 -rtg --discount 0.95 -lr 0.01 \
--use_baseline -blr 0.005 -bgs 5 --exp_name cheetah_baseline_lower_lr

baseline_loss:

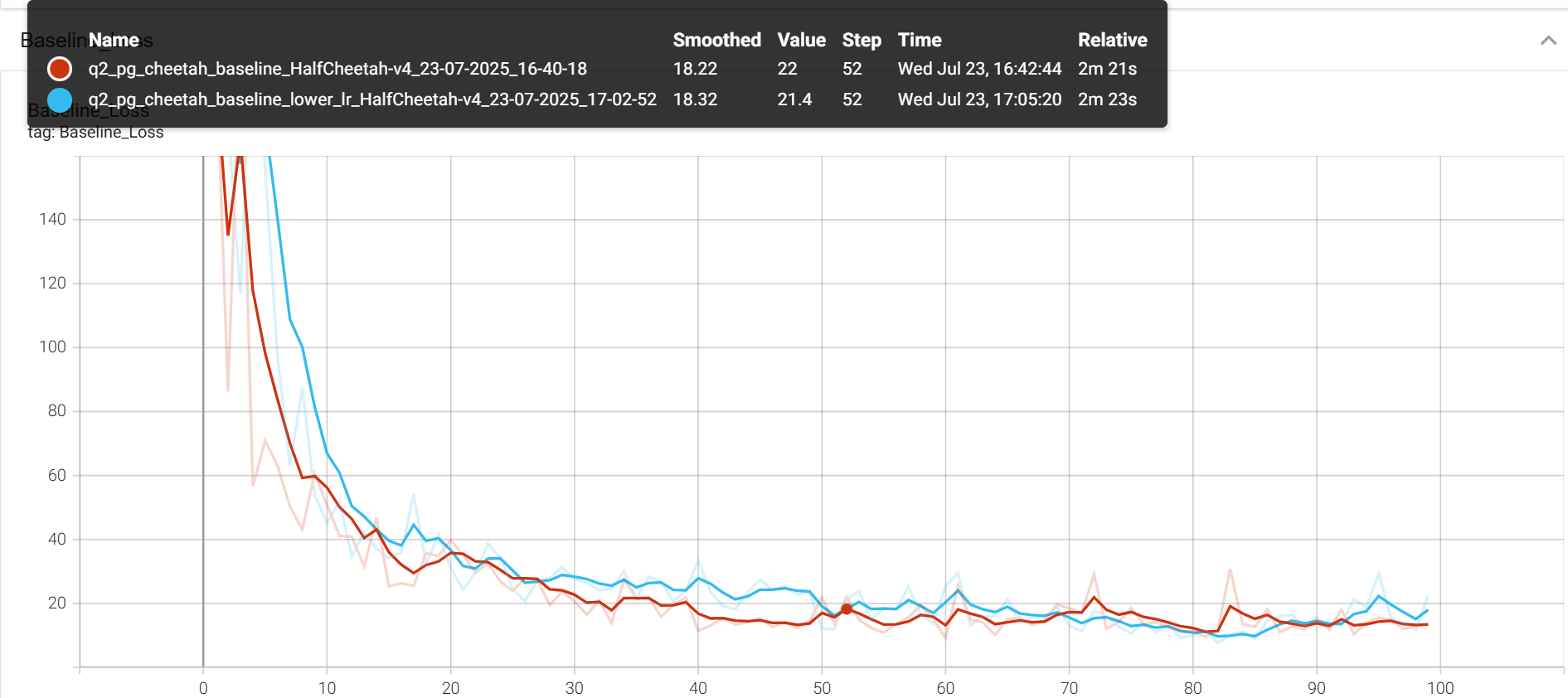
Eval_AverageReturn：

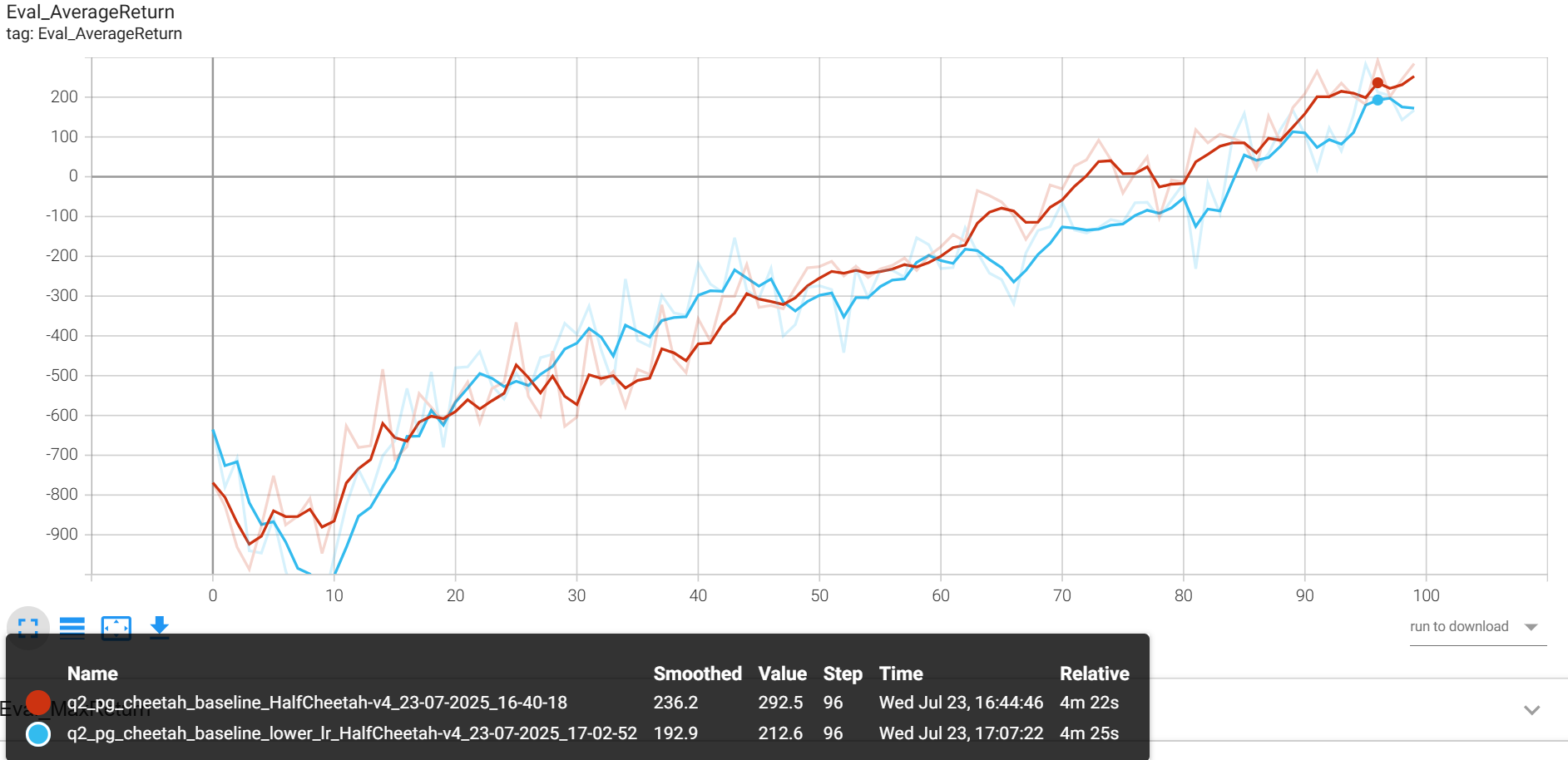
更小的bgs

python cs285/scripts/run_hw2.py --env_name HalfCheetah-v4 \
-n 100 -b 5000 -rtg --discount 0.95 -lr 0.01 \
--use_baseline -blr 0.01 -bgs 3 --exp_name cheetah_baseline_lower_lr

baseline_loss

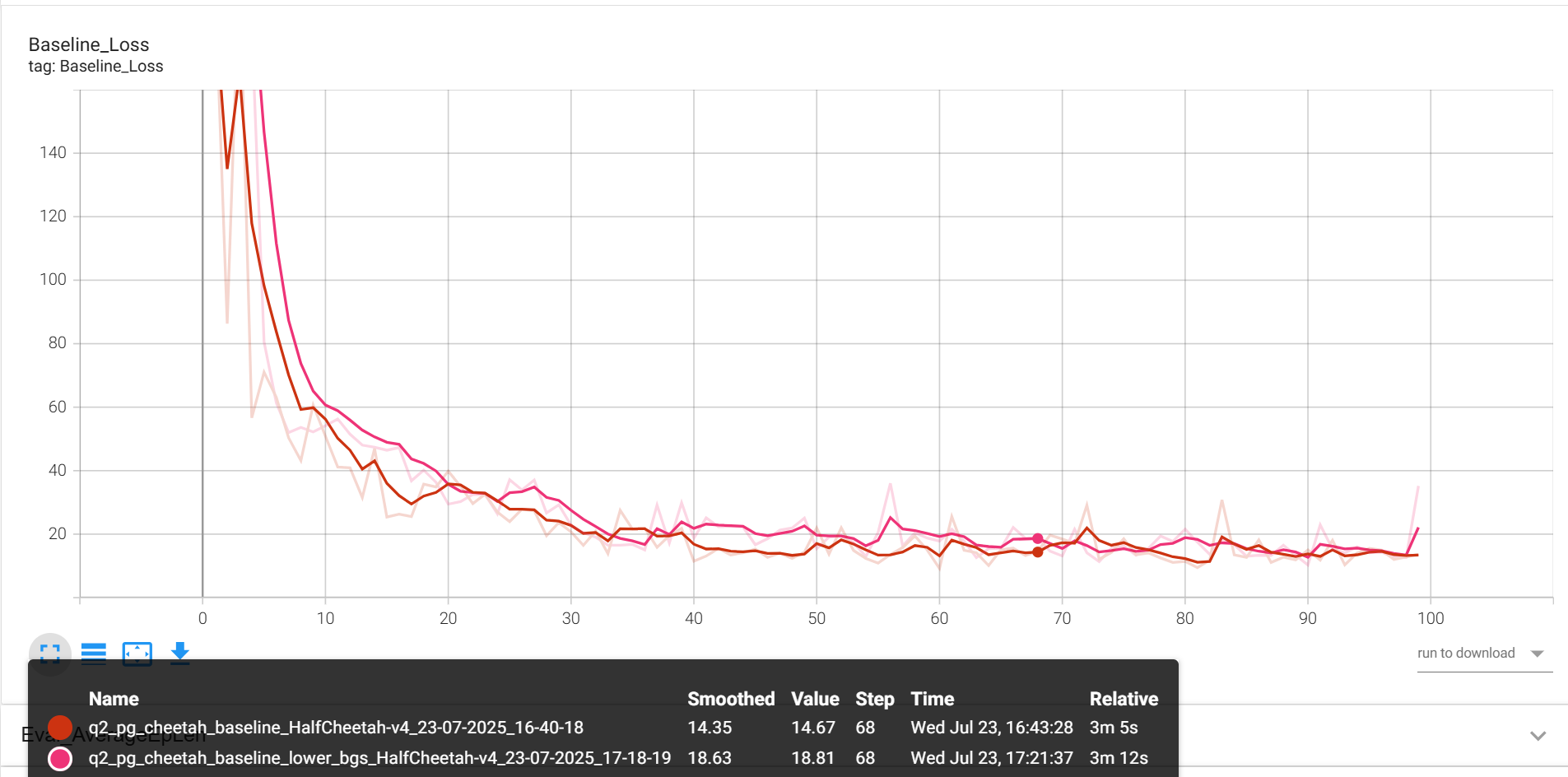
Eval_AverageReturn

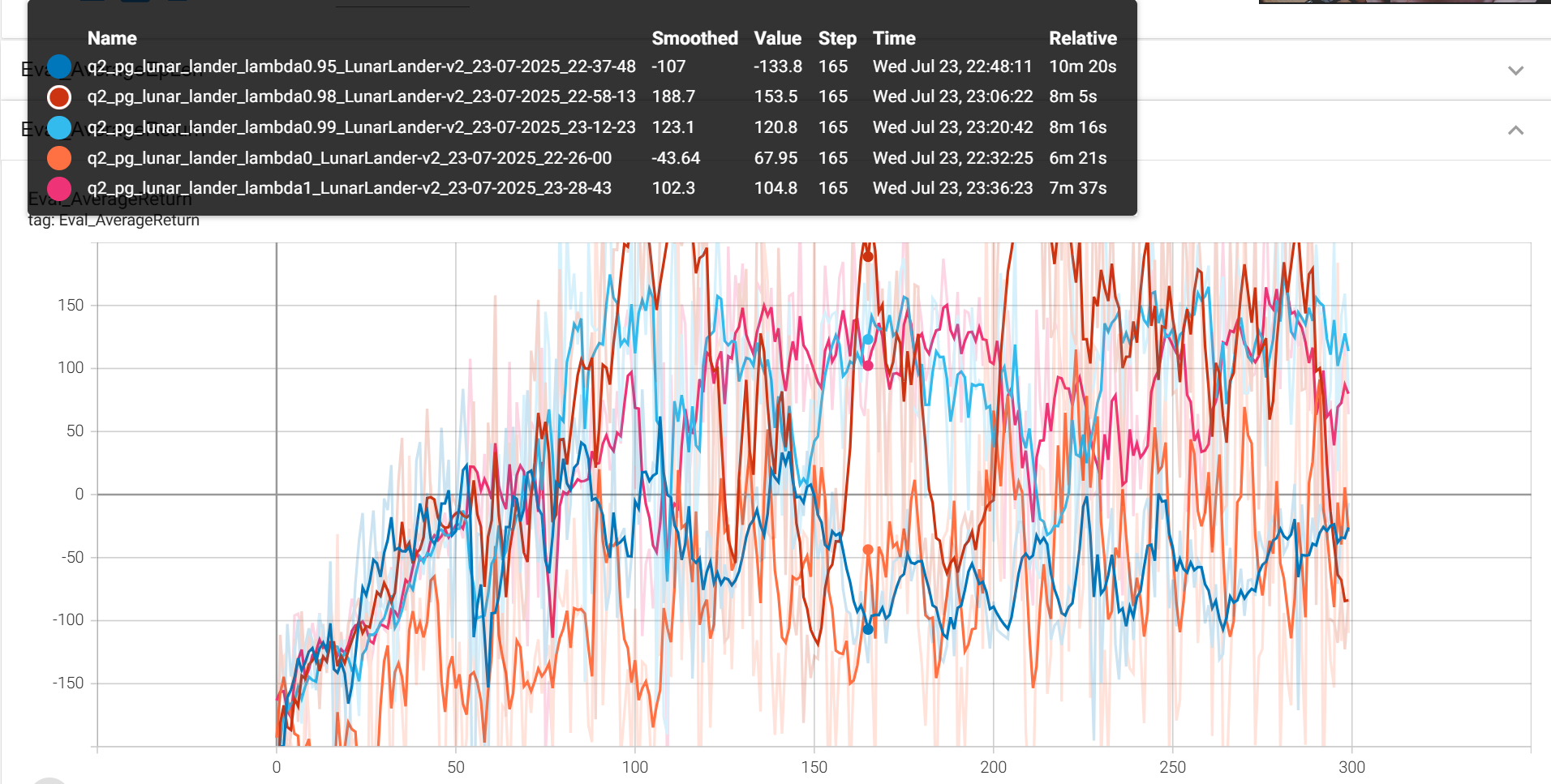
GAE的参数

python cs285/scripts/run_hw2.py \
--env_name LunarLander-v2 --ep_len 1000 \
--discount 0.99 -n 300 -l 3 -s 128 -b 2000 -lr 0.001 \
--use_reward_to_go --use_baseline --gae_lambda 0 \
--exp_name lunar_lander_lambda0
python cs285/scripts/run_hw2.py \
--env_name LunarLander-v2 --ep_len 1000 \
--discount 0.99 -n 300 -l 3 -s 128 -b 2000 -lr 0.001 \
--use_reward_to_go --use_baseline --gae_lambda 0.95 \
--exp_name lunar_lander_lambda0.95
python cs285/scripts/run_hw2.py \
--env_name LunarLander-v2 --ep_len 1000 \
--discount 0.99 -n 300 -l 3 -s 128 -b 2000 -lr 0.001 \
--use_reward_to_go --use_baseline --gae_lambda 0.98 \
--exp_name lunar_lander_lambda0.98
python cs285/scripts/run_hw2.py \
--env_name LunarLander-v2 --ep_len 1000 \
--discount 0.99 -n 300 -l 3 -s 128 -b 2000 -lr 0.001 \
--use_reward_to_go --use_baseline --gae_lambda 0.99 \
--exp_name lunar_lander_lambda0.99
python cs285/scripts/run_hw2.py \
--env_name LunarLander-v2 --ep_len 1000 \
--discount 0.99 -n 300 -l 3 -s 128 -b 2000 -lr 0.001 \
--use_reward_to_go --use_baseline --gae_lambda 1 \
--exp_name lunar_lander_lambda1

humanoid

显卡配置是A6000，在安装完以下渲染的系统依赖库（mesa依赖）

sudo apt update
sudo apt install libosmesa6-dev libgl1-mesa-glx libglfw3

仍然无法显示，尝试了使用虚拟显示，代码能正常运行，但结束后渲染出来的image为黑屏

Xvfb :99 -screen 0 1024x768x24 & 
export DISPLAY=:99

注意在使用虚拟显示结束后关闭其进程pkill -f "Xvfb :99"

后尝试关闭虚拟现实，根据installation.md里面的操作export MUJOCO_GL=egl，仍然报错

ImportError: Cannot initialize a EGL device display. This likely means that your EGL driver does not support the PLATFORM_DEVICE extension, which is required for creating a headless rendering context.

–use_reward_to_go --use_baseline --gae_lambda 1
–exp_name lunar_lander_lambda1


[外链图片转存中...(img-8TlHf299-1753346249788)]

### humanoid

显卡配置是A6000，在安装完以下渲染的系统依赖库（mesa依赖）

```python
sudo apt update
sudo apt install libosmesa6-dev libgl1-mesa-glx libglfw3

仍然无法显示，尝试了使用虚拟显示，代码能正常运行，但结束后渲染出来的image为黑屏

Xvfb :99 -screen 0 1024x768x24 & 
export DISPLAY=:99

注意在使用虚拟显示结束后关闭其进程pkill -f "Xvfb :99"

后尝试关闭虚拟现实，根据installation.md里面的操作export MUJOCO_GL=egl，仍然报错

ImportError: Cannot initialize a EGL device display. This likely means that your EGL driver does not support the PLATFORM_DEVICE extension, which is required for creating a headless rendering context.

后在run_hw2.py的前面加入os.environ["MUJOCO_GL"] = "osmesa"得以正常渲染