C C++最新力扣429 - N叉树的层序遍历【BFS+DFS】，相关资料参考

2401_84973706

于 2024-05-15 07:13:42 发布

阅读量931

点赞数 9

分类专栏：程序员文章标签： c语言 c++ 学习

本文链接：https://blog.youkuaiyun.com/2401_84973706/article/details/138887471

版权

程序员专栏收录该内容

43 篇文章

订阅专栏

网上学习资料一大堆，但如果学到的知识不成体系，遇到问题时只是浅尝辄止，不再深入研究，那么很难做到真正的技术提升。

需要这份系统化的资料的朋友，可以添加戳这里获取

一个人可以走的很快，但一群人才能走的更远！不论你是正从事IT行业的老鸟或是对IT行业感兴趣的新人，都欢迎加入我们的的圈子（技术交流、学习资源、职场吐槽、大厂内推、面试辅导），让我们一起学习成长！

最近一直在做二叉树的层次遍历相关的题，挑了一道比较经典的题给大家讲解🎓

N 叉树的层序遍历

原题描述
题型引入和分析
- 1、二叉树的层序遍历算法
  - 2、思路分析与讲解
解法一：BFS（广度优先搜索）
- 1、万能模板（！！！）
  - 2、分步详解（重要代码）
  - 3、整体代码（Java、C++）
解法二：DFS（深度优先搜索）
- 1、万能模板（！！！）
  - 2、分步详解
  - 3、整体代码（Java、C++）
总结与拓展

原题描述

给定一个 N 叉树，返回其节点值的层序遍历。（即从左到右，逐层遍历）。

树的序列化输入是用层序遍历，每组子节点都由 null 值分隔（参见示例）。

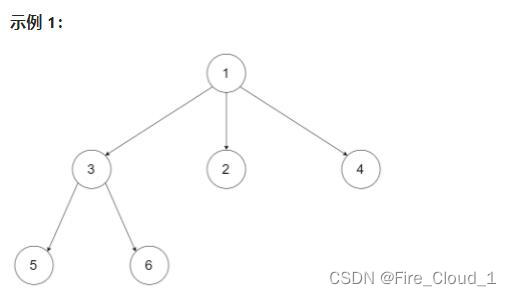
请添加图片描述

输入：root = [1,null,3,2,4,null,5,6]
输出：[[1],[3,2,4],[5,6]]

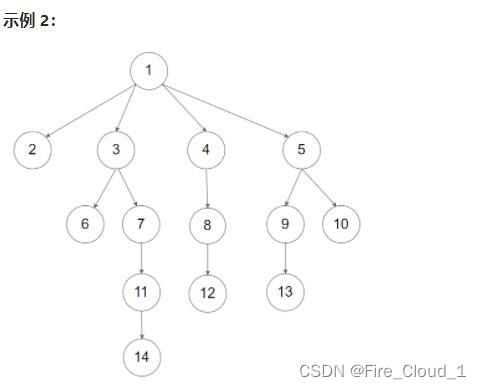
请添加图片描述

输入：root = [1,null,2,3,4,5,null,null,6,7,null,8,null,9,10,null,null,11,null,12,null,13,null,null,14]
输出：[[1],[2,3,4,5],[6,7,8,9,10],[11,12,13],[14]]

题型引入和分析

从题目背景来看，是属于层序遍历之类的题目，但是对于二叉树的层序遍历我们还是比较熟悉（鉴于可能有同学不太清楚，稍微讲一下，作为引入🎥）

1、二叉树的层序遍历算法

void LevelOrder(BTNode\* b)
{
	BTNode\* p;
	SqQueue\* qu;
	InitQueue(qu);
	
	EnQueue(qu, b);			//先将根结点入队
	while (!QueueEmpty(qu))
	{
		DeQueue(qu, p);
		printf("%c ", p->data);

		//若有左/右孩子，则将其入队
		if (p->lchild != NULL)
			EnQueue(qu, p->lchild);
		if (p->rchild != NULL)
			EnQueue(qu, p->rchild);
	}
	DestroyQueue(qu);
}

对于二叉树的层序遍历是采用环形队列的方法来，首先是先将根节点入队，在队不空时循环。在队列中出队一个结点p，访问它，若有左孩子，则将其左孩子入队；若有右孩子，则将其右孩子入队，如此操作直到队空为止，为了理解地更加形象，配了一段动画给大家理解（微信手机端看不到动画）📟

当然这只是很普通的一种算法，也是比较受大众所接受的，比较好理解，有其他高效的算法也可以层序遍历二叉树，比如下面的BFS（广度优先搜索）就不错，也是蛮高效的。看过了二叉树的层序遍历，接下来回归正题，进入本题的讲解

2、思路分析与讲解

从题目背景可以看出，无论是对于二叉树还是N叉树的层序遍历，我们优先想到的肯定是BFS（广度优先搜索），去层层遍历它的每一个结点，在其中继续寻找其有多少孩子结点，最后将遍历到的结点放入小结果集，最后放入大结果集；DFS（深度优先搜索）也是一样的套路，就是需要进行不断地递归，去寻找孩子结点，最后将结果返回

解法一：BFS（广度优先搜索）

1、万能模板（！！！）

对于BFS解决二叉树的层次遍历，有固定的模板，只要把模板记下来，遇到类似的问题拿模板去套就能慢慢出思路了，具体题目只需要在放入结果的位置稍微判断和整改即可📖

class Solution {
public:
    vector<vector<int>> levelOrder(TreeNode\* root) {
        queue<TreeNode\*> que;
        if (root != NULL) que.push(root);
        vector<vector<int>> result;
        while (!que.empty()) {
            int size = que.size();
            vector<int> vec;
            // 这里一定要使用固定大小size，不要使用que.size()，因为que.size是不断变化的
            for (int i = 0; i < size; i++) {
                TreeNode\* node = que.front();
                que.pop();
                vec.push\_back(node->val);
                if (node->left) que.push(node->left);
                if (node->right) que.push(node->right);
            }
            result.push\_back(vec);
        }
        return result;
    }
};

2、分步详解（重要代码）

首先看到🔎题目要我们返回的是一个vector<vector<>>的类型，所以定义一个结果集的容器来承装，然后对于BFS层次遍历，我们一般都会使用队列来解决，因此需要再定义一个二叉树类型的队列，然后先对根结点进行判断，若存在根结点，先将其入队

 queue<Node\*> qu;
 vector<vector<int>> result;
 if(root != NULL)    qu.push(root);

其次，就是要在队不为空时进行每层的遍历判断，一个循环便是一层，首先取到遍历当前层是队列的大小，然后去进行一个单层的遍历，取出当前队列的首元素，并将其出队，之后此结点放入小结果集，也就是为了存放一层的所有结点所定义的vec容器。
后面就是比较关键的一步，要对遍历到结点的孩子结点进行一个再次的内层遍历，去判断其是否有孩子结点，若有，则将它们全部入队

 //将遍历到的孩子结点入队
 for(int i = 0;i < node->children.size(); ++i)
     if(node->children[i])    qu.push(node->children[i]);
     //若有孩子结点，则将其入队，继而继续出队，而不是放进容器

结构顺序大致是这样

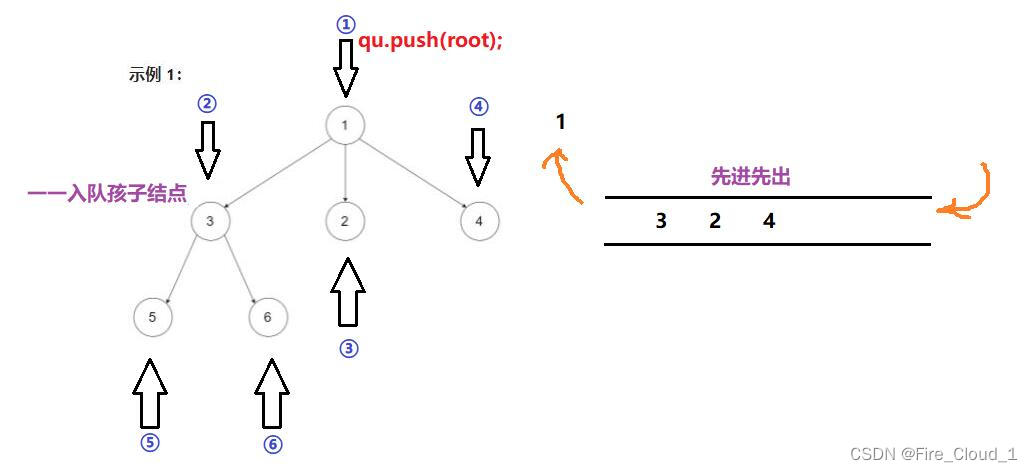
请添加图片描述

在存放完这一层的所有结点之后，因为孩子结点已入队，所以队列不为空，继续while循环的执行，这个时候就是下一层即是孩子结点所在的层的遍历，孩子结点可能又会有孩子结点，一层层遍历下去，直到碰到叶子结点为止

3、整体代码（Java、C++）

class Solution {
public:
    vector<vector<int>> levelOrder(Node\* root) {
        queue<Node\*> qu;
        vector<vector<int>> result;
        if(root != NULL)    qu.push(root);

        while(!qu.empty())
        {
            int sz = qu.size();
            vector<int> vec;

            for(int i = 0;i < sz; ++i)
            {
                Node\* node = qu.front();
                qu.pop();
                vec.push\_back(node->val);

                //将遍历到的孩子结点入队
                for(int i = 0;i < node->children.size(); ++i)
                    if(node->children[i])    qu.push(node->children[i]);
                    //若有孩子结点，则将其入队，继而继续出队，而不是放进容器
            }
            result.push\_back(vec);
        }
        return result;
    }
};

再给一种Java版本的

class Solution {
    public List<List<Integer>> levelOrder(Node root) {
        Queue<Node> qu = new LinkedList<>();
        List<List<Integer>> result = new ArrayList<>();
        if(root != null)    qu.offer(root);

        while(!qu.isEmpty())
        {
            int sz = qu.size();
            List<Integer> vec = new ArrayList<>();
            while(sz > 0)
            {
                Node node = qu.poll();
                vec.add(node.val);
                qu.addAll(node.children);
                sz--;
            }
            result.add(vec);
        }
        return result;
    }
}