c++之力扣17. 电话号码的字母组合（DFS+BFS）

题目描述：
给定一个仅包含数字 2-9 的字符串，返回所有它能表示的字母组合。
给出数字到字母的映射如下（与电话按键相同）。注意 1 不对应任何字母。

示例:
输入：“23” 输出：[“ad”, “ae”, “af”, “bd”, “be”, “bf”, “cd”, “ce”, “cf”].

看到这题目那就是遍历啊！！！，知道的遍历有二叉树的前序、中序、后序遍历和图的DFS、BFS遍历。现在想想方法就出来了，就是图的遍历。。

而深度优先遍历是基于递归，广度优先遍历则基于队列实现

一、深度优先遍历（递归回溯）
假设输入223, DFS遍历顺序则是
第一步：红色线伞种情况
第二步：蓝色线三种情况
第三步：以此类推。。。

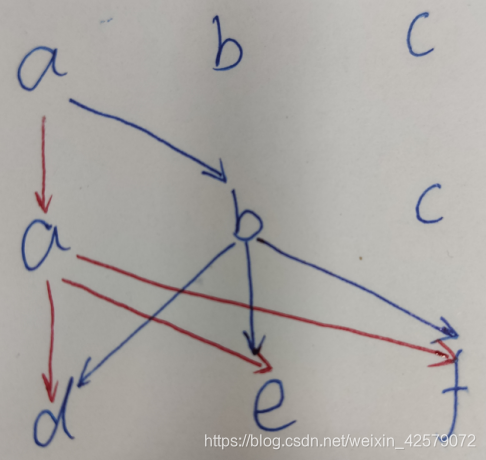
//DFS(回溯法)

#include <vector>
#include <string>
#include <iostream>
#include <unordered_map>
using namespace std;

class Solution
{
   
   
	vector<string> result;
	string digits;
	unordered_map<char, string> store= {
   
    {
   
   '2',"abc"},{
   
   '3',"def"},{
   
   '4',"ghi"},
		{
   
   '5',"jkl"},{
   
   '6',"mno"},{
   
   '7',"pqrs"},{
   
   '8',"tuv"},{
   
   '9',"wxyz"} };

public:
	vector<string> letterCombinations</