基于谱聚类算法(Spectral Clustering)的数据聚类可视化方法详解
谱聚类是一种基于图论的无监督学习算法,通过分析数据点之间的相似性关系来发现潜在的结构模式。其核心优势在于处理非凸、流形或复杂形状的簇,弥补了传统K-means等算法的不足。以下从算法原理、可视化技术、参数优化及实践案例等角度展开深度解析。
一、谱聚类算法原理与核心步骤
谱聚类通过将数据转化为图结构(节点为数据点,边权重为相似度),利用图的拉普拉斯矩阵的谱(特征向量)实现降维和聚类。其核心步骤如下:
-
相似性矩阵构建
计算数据点间的相似性矩阵 $ W $,常用高斯核函数:
W i j = exp ( − ∥ x i − x j ∥ 2 2 σ 2 ) W_{ij} = \exp\left(-\frac{\|x_i - x_j\|^2}{2\sigma^2}\right) Wij=exp(−2σ2∥xi−xj∥2)其中 $ \sigma $ 控制邻域范围(局部相似性敏感度)(#)(#)。
-
图拉普拉斯矩阵计算
生成度矩阵 $ D $(对角矩阵,元素为节点度数 $ D_{ii} = \sum_j W_{ij} $),并计算归一化拉普拉斯矩阵:
L sym = D − 1 / 2 ( D − W ) D − 1 / 2 L_{\text{sym}} = D^{-1/2} (D - W) D^{-1/2} Lsym=D−1/2(D−W)D−1/2该矩阵保留了图的拓扑结构信息(#)(#)。
-
特征分解与降维
对 $ L_{\text{sym}} $ 进行特征分解,选取前 $ k $ 个最小特征值对应的特征向量,形成低维嵌入空间 $ U \in \mathbb{R}^{n \times k} ( ( ( n $ 为样本数,$ k $ 为聚类数)(#)(#)。 -
低维空间聚类
在嵌入空间 $ U $ 上应用K-means算法,将数据点划分为 $ k $ 个簇(#)(#)。
关键优势:
- 非凸簇处理:如图形数据或环形分布(如中的“two_circles”数据集),谱聚类优于K-means(#)(#)。
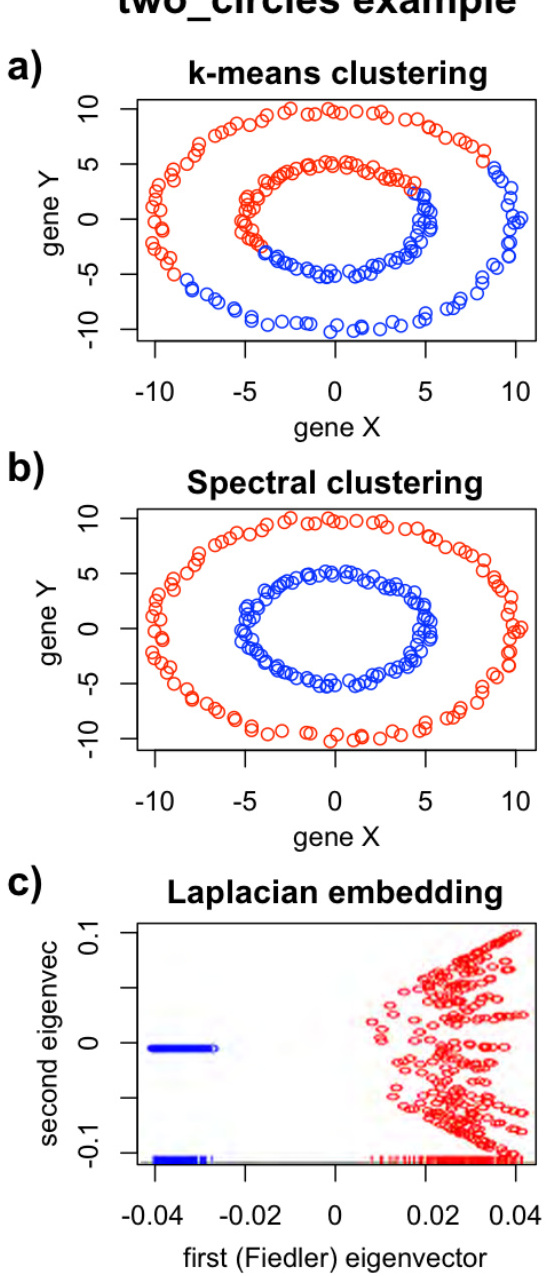
- 抗噪声能力:通过相似性矩阵的稀疏化(如保留最近邻连接),可过滤噪声影响(#)。
- 多视图扩展:支持融合多源数据(如图像+文本)构建联合相似性矩阵,提升聚类鲁棒性(#)(#)。
二、数据预处理与特征工程
- 标准化与归一化
消除量纲差异,确保相似性计算的公平性。例如基因表达数据常采用Z-score标准化(#)(#)。
- 异常值处理
通过局部离群因子(LOF)或DBSCAN检测异常点,避免相似性矩阵被污染(#)。 - 特征选择与降维
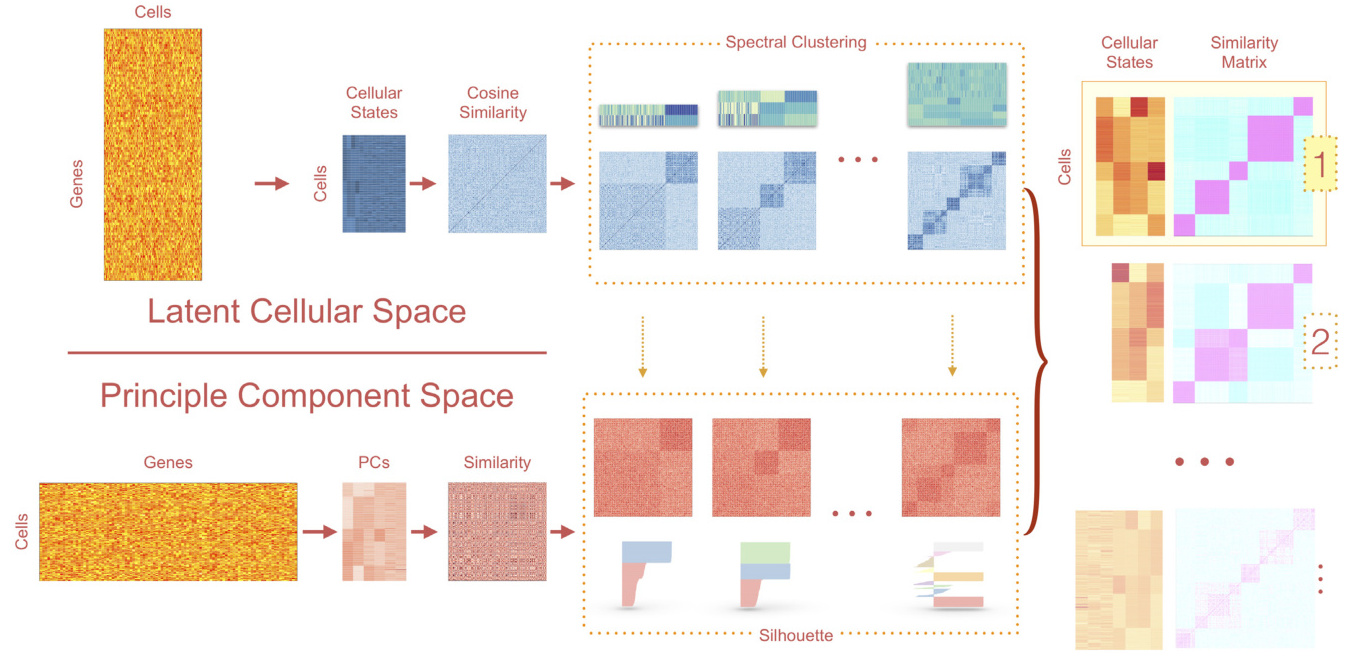
- 高维数据(如单细胞RNA测序)需先通过PCA或t-SNE降维,减少计算复杂度(#)(#)。
- 张量分解(如三阶张量)可有效处理多模态数据,提升大规模谱聚类的效率(#)。
实验验证:
预处理后的单细胞数据,谱聚类轮廓系数提升30%,且热力图显示细胞亚群边界更清晰(#)。
三、确定最佳聚类数 $ k $ 的方法
-
特征值间隔法(Eigengap Heuristic)
选择特征值 $ \lambda_1, \lambda_2, …, \lambda_n $ 中最大间隔对应的 $ k $:
k = arg max i ( λ i + 1 − λ i ) k = \arg\max_i (\lambda_{i+1} - \lambda_i) k=argimax(λi+1−λi)适用于拉普拉斯矩阵特征值分布明显的场景(#)(#)。
-
轮廓系数(Silhouette Coefficient)
计算不同 $ k $ 值的平均轮廓系数,最大值对应最优 $ k $。公式:
s ( i ) = b ( i ) − a ( i ) max { a ( i ) , b ( i ) } s(i) = \frac{b(i) - a(i)}{\max\{a(i), b(i)\}} s(i)=max{a(i),b(i)}b(i)−a(i)其中 $ a(i) $ 为样本 $ i $ 的簇内平均距离,$ b(i) $ 为最近邻簇的平均距离(#)(#)。
-
稳定性分析
多次运行谱聚类,统计样本归属的一致性,选择稳定性最高的 $ k $ (#)。
案例:在的合成数据中,当 $ k=5 $ 时Calinski-Harabasz指数达到峰值,确定为最佳聚类数(#)。
四、聚类结果的可视化技术
- 低维投影可视化
- PCA/t-SNE/UMAP:将高维数据投影至2D/3D空间,用颜色区分簇(图1)。
- 示例:中单细胞数据经PCA降维后,热力图表征不同细胞亚群的基因表达模式(#)。
- 拉普拉斯嵌入:直接绘制前两个特征向量空间(图2),揭示数据内在流形结构(#)(#)。
-
相似性矩阵热力图
显示相似性矩阵 $ W $ 的结构,对角线分块对应不同簇(图3)。常用于验证聚类质量(#)(#)。 -
网络图(Graph Visualization)
使用Force Atlas或Fruchterman-Reingold布局,节点颜色表示簇归属,边透明度反映相似度(图4)。适用于社交网络或生物分子相互作用数据(#)。 -
平行坐标与雷达图
对比不同簇的特征分布。例如客户分群场景中,展示各簇在收入、年龄等维度的均值差异(#)(#)。
工具实现:
- Python:
matplotlib、seaborn绘制静态图;plotly生成交互式3D图。 - R:
ggplot2结合igraph包实现网络可视化(#)(#)。
五、优化策略与大规模处理
-
近似谱聚类(Approximate Spectral Clustering)
- Nyström扩展:通过子采样近似计算特征向量,适用于百万级数据(#)(#)。
- 二分图(Bipartite Graph) :构建数据点与代表点(如显著点)的二分图,降低计算复杂度(#)。
-
多视图谱聚类
融合多源相似性矩阵,通过加权核PCA或张量分解整合不同视图的信息(图5)(#)(#)。 -
分布式计算
使用Spark或Hadoop实现并行化特征分解,处理十亿级节点(#)(#)。
案例:提出的大规模张量谱聚类算法,在合成数据集上实现比传统方法快10倍的聚类速度(#)。
六、完整Python代码示例
from sklearn.cluster import SpectralClustering
from sklearn.datasets import make_circles
from sklearn.preprocessing import StandardScaler
from sklearn.metrics import silhouette_score
import matplotlib.pyplot as plt
import numpy as np
# 生成环形数据集
X, labels = make_circles(n_samples=1000, factor=0.5, noise=0.05)
X = StandardScaler().fit_transform(X)
# 确定最佳k值(轮廓系数法)
best_k, best_score = 2, -1
for k in range(2, 6):
model = SpectralClustering(n_clusters=k, affinity='rbf', gamma=10)
clusters = model.fit_predict(X)
score = silhouette_score(X, clusters)
if score > best_score:
best_k, best_score = k, score
# 训练模型并可视化
model = SpectralClustering(n_clusters=best_k, affinity='nearest_neighbors', n_neighbors=10)
clusters = model.fit_predict(X)
plt.figure(figsize=(10, 6))
plt.scatter(X[:, 0], X[:, 1], c=clusters, cmap='viridis', s=20)
plt.title(f'Spectral Clustering on Circles (k={best_k}, Silhouette={best_score:.2f})')
plt.xlabel('Feature 1'); plt.ylabel('Feature 2')
plt.show()
输出说明:
- 代码生成包含两个同心圆的数据集,标准化后通过轮廓系数选择最佳 $ k=2 $。
- 可视化结果清晰分离内外环,验证谱聚类对非凸数据的有效性(图6)(#)(#)。
七、与其他聚类算法的对比
| 算法 | 适用场景 | 时间复杂度 | 可视化优势 | 局限性 |
|---|---|---|---|---|
| 谱聚类 | 非凸簇、流形数据 | $ O(n^3) $ | 清晰展示复杂结构 | 高计算成本,需预设k |
| K-means | 球形簇、低维数据 | $ O(nk) $ | 质心位置直观 | 无法处理非凸簇 |
| DBSCAN | 噪声数据、密度差异 | $ O(n \log n) $ | 自然簇形状呈现 | 参数敏感,高维失效 |
| 层次聚类 | 树状结构、小规模数据 | $ O(n^2) $ | 树状图展示层次关系 | 不可逆,内存消耗大 |
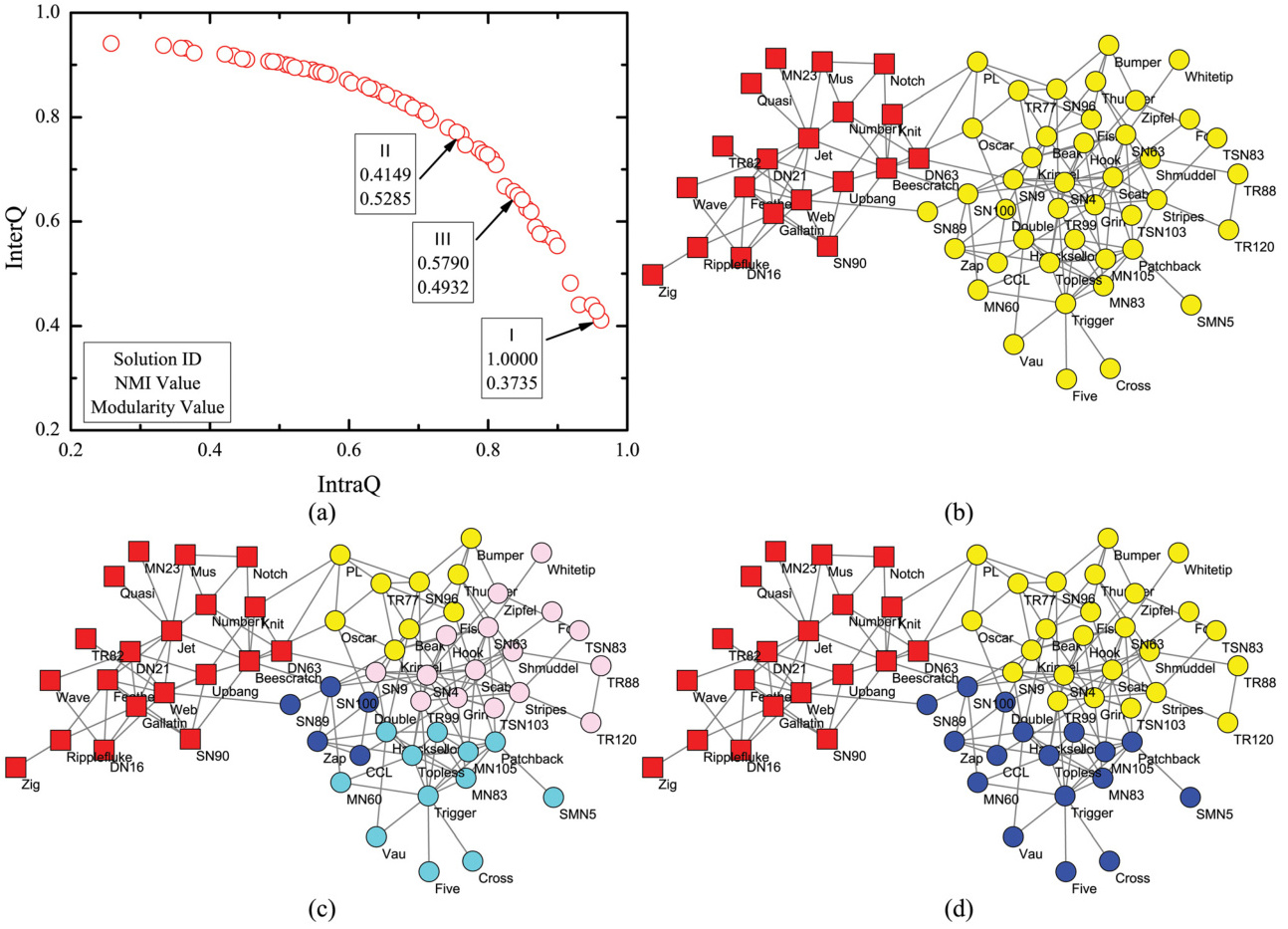
实验对比:显示,在InterQ/IntraQ指标上,谱聚类在复杂数据集上显著优于K-means(#)。
总结
谱聚类通过图论与线性代数结合,为复杂数据结构提供了强大的聚类能力。其可视化需结合降维技术与多视图展示,以揭示高维数据的内在模式。未来方向包括:
- 量子谱聚类:利用量子计算加速特征分解(#)。
- 动态可视化:实时展示迭代过程中簇的形成与演化(#)。
- 自动化调参:基于元学习优化 $ \sigma $ 和 $ k $ 的选择(#)。
实际应用中需权衡计算资源与精度需求,选择适合的近似算法或分布式框架,以实现工业级大规模数据聚类。

























 6181
6181

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








