一、数组
数组操作中用到的方法:二分,双指针(快慢指针、首尾指针),滑动窗口
1.【二分查找】
该题要注意的坑点就是开区间还是闭区间的问题。
思路:区间的定义有两种,左闭右闭或者左闭右开。先说左闭右闭,此时判断条件一定是while(left <= right),因为left==right是有意义的。
class Solution {
public:
int search(vector<int>& nums, int target) {
int n = nums.size();
int left = 0, right = n - 1;
while(left <= right){
int mid = (left + right) >> 1;
if(nums[mid] < target){
left = mid + 1;
}
else if(nums[mid] > target){
right = mid - 1;
}else{
return mid;
}
}
return -1;
}
};
//时间复杂度O(logn)
//空间复杂度O(1)再说左闭右开,首先边界条件变为while(left < right),因为left==right没有意义,其次要注意right的初值,因为是右开,所以考虑到数组只有一个元素的情况下,初值设为nums.size()即可。最后注意当nums[mid] > target 时,right = mid,因为开区间导致下一个查询区间不回去寻找nums[mid]
class Solution {
public:
int search(vector<int>& nums, int target) {
int n = nums.size();
int left = 0, right = n;
while(left < right){
int mid = (left + right) >> 1;
if(nums[mid] < target){
left = mid + 1;
}
else if(nums[mid] > target){
right = mid;
}else{
return mid;
}
}
return -1;
}
};
//时间复杂度O(logn)
//空间复杂度O(1)2.【移除元素】
第一反应是用vector.erase()方法来做,erase会删除指定位置的元素,并自动将后续元素移动填补被删除的位置,从而保持数组中元素的连续性。
顺便复习一下顺序容器,比如vector,deque,list的几个操作
push_back(val),pop_back(),insert(pos, val),erase(),该方法的缺点就是时间复杂度开销大
class Solution {
public:
int removeElement(vector<int>& nums, int val) {
for(int i = 0; i < nums.size(); i++){
if(nums[i] == val){
nums.erase(nums.begin() + i);
i--;
}
}
return nums.size();
}
};
//时间复杂度O(n^2)
//空间复杂度O(1)接下来使用双指针(快慢指针)的解法,原因:快指针去找不等于val的,慢指针更新新数组的下标
class Solution {
public:
int removeElement(vector<int>& nums, int val) {
//使用快慢指针来做
int slowIndex = 0;
for(int fastIndex = 0; fastIndex < nums.size(); fastIndex++){
if(nums[fastIndex] != val){
nums[slowIndex] = nums[fastIndex];
slowIndex++;
}
}
return slowIndex;
}
};
//时间复杂度O(n)
//空间复杂度O(1)3.【有序数组的平方】
思路:第一反应是所有元素平方之后重新排序,但是没用到“非递减数列”这条信息
class Solution {
public:
vector<int> sortedSquares(vector<int>& nums) {
for(int i = 0; i < nums.size(); i++){
nums[i] = nums[i] * nums[i];
}
sort(nums.begin(), nums.end());
return nums;
}
};
//时间复杂度O(nlogn)
//空间复杂度O(n)再说这题为什么会想到用双指针的方法呢, 原因是这个数组的特点是所有元素平方之后,最大值一定产生于两端,最小值一定是在中间,即平方之后,数组大小从两端递减到中间。
提交中遇到的一个溢出问题:
直接在原数组上进行更改,nums[k] = nums[beginIndex] * nums[beginIndex]系统判定会发生int溢出的问题。修改策略:一种是根治,修改整数类型,来存放平方后的结果,一种是由于测试用例不会给溢出范围的值,所以重新定义一个result数组,用来存放结果,而不是直接在原数组上修改。
错误代码:
//错误代码
class Solution {
public:
vector<int> sortedSquares(vector<int>& nums) {
//首尾指针,比较平方后的大小,再将新数组从尾开始赋值
int beginIndex = 0, endIndex = nums.size() - 1;
int k = nums.size() - 1;
while(beginIndex <= endIndex){
if(nums[beginIndex] * nums[beginIndex] >= nums[endIndex] * nums[endIndex]){
nums[k] = nums[beginIndex] * nums[beginIndex];
beginIndex++;
}else{
nums[k] = nums[endIndex] * nums[endIndex];
endIndex--;
}
k--;
}
return nums;
}
};修改后:
//正确代码
class Solution {
public:
vector<int> sortedSquares(vector<int>& nums) {
//首尾指针,比较平方后的大小,再将新数组从尾开始赋值
int beginIndex = 0, endIndex = nums.size() - 1;
int k = nums.size() - 1;
vector<int> result(nums.size());
while(beginIndex <= endIndex){
if(nums[beginIndex] * nums[beginIndex] >= nums[endIndex] * nums[endIndex]){
result[k] = nums[beginIndex] * nums[beginIndex];
beginIndex++;
}else{
result[k] = nums[endIndex] * nums[endIndex];
endIndex--;
}
k--;
}
return result;
}
};
//时间复杂度O(n)
//空间复杂度O(n)*4.【长度最小的子数组】
思路:没思路,本来想法是先排序,然后查找有没有target,有的话返回1,没有的话再双指针去找,但是想不出来怎么返回最小长度。。。看过解析之后,使用滑动窗口(不断的调整子数列的起始位置和终止位置从而得到想要的结果)。核心:while(sum >= target) 判断部分
class Solution {
public:
int minSubArrayLen(int target, vector<int>& nums) {
int result = INT32_MAX;
int subLength = 0;//记录滑动窗口的长度
int i = 0;//滑动窗口起始位置
int sum = 0;//滑动窗口的和
for(int j = 0; j < nums.size(); j++){
sum += nums[j];
while(sum >= target){
subLength = j - i + 1;
result = result < subLength ? result : subLength;
sum -= nums[i++];
}
}
return result == INT32_MAX ? 0 : result;
}
};
//时间复杂度O(n)
//空间复杂度O(1)*5.【螺旋矩阵】
不是很有思路,直接看解析。参照K神解析,感觉这个版本比较容易理解,尤其是迭代条件while(num <= end) 简单易懂,此外学了一手二维矩阵初始化result(n, vector<int>(n, 0))
class Solution {
public:
vector<vector<int>> generateMatrix(int n) {
int left = 0, right = n - 1, top = 0, down = n - 1;
vector<vector<int>> result(n, vector<int>(n, 0));
int num = 1, end = n * n;
while(num <= end){
//从左到右
for(int i = left; i <= right; i++){
result[top][i] = num++;
}
top++;
//从上到下
for(int i = top; i <= down; i++){
result[i][right] = num++;
}
right--;
//从右到左
for(int i = right; i >= left; i--){
result[down][i] = num++;
}
down--;
//从下到上
for(int i = down; i >= top; i--){
result[i][left] = num++;
}
left++;
}
return result;
}
};
//时间复杂度O(n^2)
//空间复杂度O(n^2)6.【无重复字符的最长子串】
思路:滑动窗口+哈希set
find()函数用于查找指定元素,如果找到返回指向该元素的迭代器,如果找不到返回set.end()
class Solution {
public:
int lengthOfLongestSubstring(string s) {
int left = 0;
unordered_set<int> set;
int maxStreak = 0;
for(int right = 0; right < s.size(); right++){
//当有重复子串出现时,移动左指针,删除最左字符
while(set.find(s[right]) != set.end()){
set.erase(s[left]);
left++;
}
//删除之后记得加入当前字符元素
set.insert(s[right]);
maxStreak = max(maxStreak, right - left + 1);
}
return maxStreak;
}
};7.【找到字符串中所有字母异位词】
class Solution {
public:
vector<int> findAnagrams(string s, string p) {
vector<int> result;
if(s.length() < p.length()) return result;
unordered_map<char, int> sCount, pCount;
int left = 0, right = 0;
//统计p的字符
for(char c : p){
pCount[c]++;
}
//滑动窗口统计s字符串
while(right < s.length()){
//先统计s字符
sCount[s[right]]++;
//如果长度相等
if(right - left + 1 == p.size()){
if(sCount == pCount){
result.push_back(left);
}
sCount[s[left]]--;
if(sCount[s[left]] == 0){
sCount.erase(s[left]);
}
left++;
}
right++;
}
return result;
}
};8.【和为k的子数组】
思路:前缀和,寻找前缀和 - k 是否存在于数组
class Solution {
public:
int subarraySum(vector<int>& nums, int k) {
int result = 0;
unordered_map<int, int> map;//存储前缀和及其出现次数
int sum = 0;
map[0] = 1;//初始化前缀和为0,出现一次
for(int i = 0; i < nums.size(); i++){
sum += nums[i];
//检查是否存在前缀和sum - k
if(map.count(sum - k)){
result += map[sum - k];
}
//记录当前前缀和出现的次数
map[sum]++;
}
return result;
}
};9.【最小覆盖子串】
class Solution {
public:
string minWindow(string s, string t) {
if(s.empty() || t.empty()) return "";
//统计t的字符个数
unordered_map<char, int> t_map;
for(char c : t){
t_map[c]++;
}
//窗口内字符的数量
unordered_map<char, int> windows_map;
int left = 0, right = 0;
int minLength = INT_MAX;
int start = 0;
int required = t_map.size();
int formed = 0;//表示当前窗口内有多少种字符达到了t的需求
//开始滑动窗口
while(right < s.size()){
char c = s[right];
windows_map[c]++;
//如果当前c出现的次数达到了t的要求
//t_map.find(c) != t_map.end()这一步是为了避免不要的windows_map统计,避免性能上的冗余计算
if(t_map.find(c) != t_map.end() && windows_map[c] == t_map[c]){
formed++;
}
//t中所有字符都满足,开始收缩窗口
while(left <= right && required == formed){
//更新最小子串
if(right - left + 1 < minLength){
minLength = right - left + 1;
start = left;
}
//收缩窗口
char left_char = s[left];
windows_map[left_char]--;
if(t_map.find(left_char) != t_map.end() && windows_map[left_char] < t_map[left_char]){
formed--;
}
left++;
}
//t中字符还未满足
right++;
}
//返回最小覆盖子串
return minLength == INT_MAX ? "" : s.substr(start, minLength);
}
};
10.【最大子数组和】
思路:比较当前值和当前值+currentSum
class Solution {
public:
int maxSubArray(vector<int>& nums) {
int currentSum = nums[0];
int sumMax = nums[0];
for(int i = 1; i < nums.size(); i++){
//如果nums[i]比currentSum + nums[i]大,说明新的子数组从当前开始更好,否则,currentSum + nums[i]
currentSum = max(nums[i], currentSum + nums[i]);
sumMax = max(sumMax, currentSum);
}
return sumMax;
}
};
11.【合并区间】
思路:这里容易产生一个误区,即每个区间只有两个值,nums[0]和nums[1]
class Solution {
public:
vector<vector<int>> merge(vector<vector<int>>& intervals) {
if(intervals.empty()) return {};
//sort只对每个数组的第一个数字进行排序
sort(intervals.begin(), intervals.end());
vector<vector<int>> result;
result.push_back(intervals[0]);
for(int i = 1; i < intervals.size(); i++){
vector<int>& last = result.back();
vector<int>& current = intervals[i];
if(current[0] <= last[1]){
last[1] = max(current[1], last[1]);
}else{
result.push_back(intervals[i]);
}
}
return result;
}
};12.【轮转数组】
//reverse用法,包含起始位置,不包含终止位置。
思路:轮转数组是一道技巧题,分三步,第一步reverse整个数组;第二步reverse(nums.begin(), nums.begin()+k);第三步reverse(nums.begin()+k, nums.end());
注意:如果不加 k = k % nums.size();,当 k 大于或等于 nums.size() 时,程序会出现 超出范围 的错误,或者导致逻辑错误。
class Solution {
public:
void rotate(vector<int>& nums, int k) {
k = k % nums.size();
reverse(nums.begin(), nums.end());
reverse(nums.begin(), nums.begin() + k);
reverse(nums.begin() + k, nums.end());
}
};排序
1.排序数组(快排)
思路:
1.首先设定一个分界值,通过该分界值将数组分为左右两部分;
2.小于等于数据集的放到左边,大于等于数据集的放到右边;
3.对于左右两部分,再次递归。
一开始是按照一个指针移动来写的,即只分为key值的左边和右边,如果遇到有多个相同key值的情况,并没有考虑设置一个中间区域,来优化时间复杂度。
partitionThreeWay() 需要 left 和 right 作为引用参数,以便 quickSort() 正确跳过等于 pivot 的区域,提高性能!
srand(time(0))初始化随机数种子,确保rand()每次运行都会产生不同的随机数。rand() % (r - l + 1)生成[l, r]范围内的随机索引,用于随机选择pivot,防止最坏情况O(n²)。
class Solution {
public:
// **三向切分快速排序**
void partitionThreeWay(vector<int>& nums, int pivot, int l, int r, int& left, int& right) {
left = l;
right = r;
int i = left;
while (i <= right) {
if (nums[i] < pivot) {
swap(nums[i], nums[left]);
left++;
i++;
} else if (nums[i] > pivot) {
swap(nums[i], nums[right]);
right--;
} else {
i++; // 如果 nums[i] == pivot,直接跳过
}
}
}
// **快速排序**
void quickSort(vector<int>& nums, int l, int r) {
if (l >= r) return;
int pivot = nums[l + rand() % (r - l + 1)]; // **随机选择 pivot**
int leftPartition, rightPartition;
partitionThreeWay(nums, pivot, l, r, leftPartition, rightPartition);
quickSort(nums, l, leftPartition - 1);
quickSort(nums, rightPartition + 1, r);
}
vector<int> sortArray(vector<int>& nums) {
srand(time(0)); // **设定随机种子**
quickSort(nums, 0, nums.size() - 1);
return nums;
}
};


矩阵
1.【矩阵置零】
思路:这题就是五个步骤,记住了就能做出来
第一二步,检查第一行、第一列是否有零,有的话就作标记,为后续整行整列清零准备。(避免错误地清零整个第一行或第一列,确保 matrix[0][0] 只是一个标记,而 firstRowZero / firstColZero 决定最终是否要清零第一行和第一列。)
第三步,遍历数组,遇到0,此时再用第一行和第一列作标记;
第四步,遍历数组,使用第一行和第一列的标记来置零;
第五步,单独处理第一行和第一列。
class Solution {
public:
void setZeroes(vector<vector<int>>& matrix) {
int m = matrix.size(), n = matrix[0].size();
bool firstRowZero = false, firstColZero = false;
//检查第一行是否有零
for(int i = 0; i < n; i++){
if(matrix[0][i] == 0){
firstRowZero = true;
break;
}
}
//检查第一列是否有零
for(int i = 0; i < m; i++){
if(matrix[i][0] == 0){
firstColZero = true;
break;
}
}
//检查剩余是否有零,用第一行第一列来标记
for(int i = 1; i < m; i++){
for(int j = 1; j < n; j++){
if(matrix[i][j] == 0){
matrix[i][0] = 0;
matrix[0][j] = 0;
}
}
}
//根据标记置零
for(int i = 1; i < m; i++){
for(int j = 1; j < n; j++){
if(matrix[i][0] == 0 || matrix[0][j] == 0){
matrix[i][j] = 0;
}
}
}
//处理第一行
if(firstRowZero){
for(int j = 0; j < n; j++){
matrix[0][j] = 0;
}
}
//检查第一列
if(firstColZero){
for(int j = 0; j < m; j++){
matrix[j][0] = 0;
}
}
}
};
2.【螺旋矩阵】
思路:绕着圈的遍历
class Solution {
public:
vector<int> spiralOrder(vector<vector<int>>& matrix) {
vector<int> result;
if(matrix.empty() || matrix[0].empty()){
return result;
}
int m = matrix.size(), n = matrix[0].size();
int top = 0, bottom = m - 1, left = 0, right = n - 1;
while(top <= bottom && left <= right){
//从左到右遍历顶部行
for(int i = left; i <= right; i++){
result.push_back(matrix[top][i]);
}
top++;
//从上到小遍历右侧列
for(int i = top; i <= bottom; i++){
result.push_back(matrix[i][right]);
}
right--;
//从右到左遍历底部行
if(top <= bottom){
for(int i = right; i >= left; i--){
result.push_back(matrix[bottom][i]);
}
bottom--;
}
//从下到上遍历左侧列
if(left <= right){
for(int i = bottom; i >= top; i--){
result.push_back(matrix[i][left]);
}
left++;
}
}
return result;
}
};
二、链表
链表理论基础
链表这部分基础不咋地,记录一些基础学习。
链表节点定义:
struct ListNode{
int val;//节点上存储的元素
ListNode *next;//指向下一节点的指针
ListNode(int x) : val(x), next(NULL) {}//节点的构造函数
};如果不定义构造函数的话,使用默认构造函数,在初始化的时候不能直接赋值。
//通过自己定义构造函数初始化节点
ListNode* head = new ListNode(5);
//通过默认构造函数初始化节点
ListNode* head = new ListNode();
head -> val = 5;
比较一下链表和数组的性能优缺点,以及分别什么时候来使用。
| 插入/删除 时间复杂度 | 查询 时间复杂度 | 适用场景 | |
| 数组 | O(n) | O(1) | 数据量固定,频繁查询,较少增删 |
| 链表 | O(1) | O(n) | 数据量不固定,频繁增删,较少查询 |
记得删除链表节点之后,及时清理内存。
1.【移除链表元素】
三种做法:1.直接使用原来的链表进行删除操作。但此时要注意如果头节点需要删除怎么办,因为移除头节点和移除其他节点是不一样的,我们删除其他节点是通过其前一个节点来进行删除操作的,而头节点是没有前一个节点的。所以移除头节点就需要将其向后移动一位,那么就要单独写一段逻辑来处理头节点,记得释放内存。
//直接使用原来的链表进行移除节点操作
class Solution {
public:
ListNode* removeElements(ListNode* head, int val) {
//删除非头节点
ListNode* cur = head;
while(cur != nullptr && cur -> next != nullptr){
if(cur -> next -> val == val){
ListNode* tmp = cur -> next;
cur -> next = cur -> next -> next;
delete tmp;
}else{
cur = cur -> next;
}
}
//删除头节点
while(head != nullptr && head -> val == val){
ListNode* tmp = head;
head = head -> next;
delete tmp;
}
return head;
}
};
//时间复杂度O(n)
//空间复杂度O(1)2.创建虚拟头节点
关键是创建之后,虚拟节点要指向头节点
class Solution {
public:
ListNode* removeElements(ListNode* head, int val) {
ListNode* dummynode = new ListNode(0);
dummynode -> next = head;
ListNode* cur = dummynode;
while(cur -> next != NULL){
if(cur -> next -> val == val){
ListNode* tmp = cur -> next;
cur -> next = cur -> next -> next;
delete tmp;
}else{
cur = cur -> next;
}
}
head = dummynode -> next;
delete dummynode;
return head;
}
};
//时间复杂度O(n)
//空间复杂度O(1)3.迭代法,逻辑主要分为三个部分:头节点为空,头节点即为val(新创建一个节点,删除原头节点,令新节点为头节点),除头节点外,其余节点为val
class Solution {
public:
ListNode* removeElements(ListNode* head, int val) {
if(head == nullptr){
return nullptr;
}
if(head -> val == val){
ListNode* newHead = removeElements(head -> next, val);
delete head;
return newHead;
}else{
head -> next = removeElements(head -> next, val);
return head;
}
}
};
//时间复杂度O(n)
//空间复杂度O(n)*2.【设计链表】
看到这道题,两眼一发黑,链表真是学不懂一点啊。。。看下解析,说是这道题的五个接口涉及了链表的常见五种操作,nice 学!
温故下链表的常见两种操作,直接在原链表上进行操作 or 创建虚拟头节点。一般建议采用创建虚拟头节点。
对这道题的一些理解写到代码注释里面了,确实搞懂这道题之后,对链表不是很畏惧了
class MyLinkedList {
public:
//定义链表节点结构体
struct listNode{
int val;
listNode* next;
listNode(int val): val(val), next(nullptr){}
};
//初始化链表
MyLinkedList() {
_dummyHead = new listNode(0);
_size = 0;//有效节点数量,即有效索引值为(0, _size - 1)
}
//获取第index个节点的数值
int get(int index) {
//index是非法数值时,返回-1
if(index < 0 || index > _size - 1){
return -1;
}
//链表的索引查询时间复杂度为O(n)
listNode* cur = _dummyHead -> next;
while(index--){
cur = cur -> next;
}
return cur -> val;
}
//在链表的前面插入一个新的节点
void addAtHead(int val) {
listNode* newHead = new listNode(val);
newHead -> next = _dummyHead -> next;
_dummyHead -> next = newHead;
_size++;
}
//在链表的末尾加入新的节点
void addAtTail(int val) {
listNode* newTail = new listNode(val);
listNode* cur = _dummyHead;
while(cur -> next != nullptr){
cur = cur -> next;
}
cur -> next = newTail;
_size++;
}
//在指定索引位置处加入新的节点
void addAtIndex(int index, int val) {
//此时要注意判断index是否为有效索引,并且如果index<0,要令index=0
if(index > _size) return;
if(index < 0) index = 0;
listNode* newNode = new listNode(val);
listNode* cur = _dummyHead;
while(index--){
cur = cur -> next;
}
newNode -> next = cur -> next;
cur -> next = newNode;
_size++;
}
//这里要注意释放内存之后,tmp指针会成为野指针,所以要指定指向空
void deleteAtIndex(int index) {
if(index >= _size || index < 0) return;
listNode* cur = _dummyHead;
while(index--){
cur = cur -> next;
}
listNode* tmp = cur -> next;
cur -> next = cur -> next -> next;
delete tmp;
tmp = nullptr;
_size--;
}
private:
int _size; // 链表中有效节点的数量
listNode* _dummyHead; // 虚拟头结点指针
};*3.【反转链表】
逻辑:反转指针方向
法一:双指针
class Solution {
public:
ListNode* reverseList(ListNode* head) {
ListNode* pre = nullptr;
ListNode* cur = head;
ListNode* tmp;
while(cur){
tmp = cur -> next;
cur -> next = pre;
pre = cur;
cur = tmp;
}
return pre;
}
};
时间复杂度:O(n)
空间复杂度:O(1)法二:递归(感觉啰嗦了 等我理解了再来写)
* 4.【两两交换链表中的的节点】
官方给的这个图就很清晰明了,我一开始不太理解为什么要有步骤三,步骤一、二就是将前两个节点交换位置,那么接下来我直接从第三个节点开始处理不就好了吗,为啥还要步骤三呢,后来想清楚,步骤二做完之后,总要指明接下来的链表方向。基本思路就是三个节点为一组。
class Solution {
public:
ListNode* swapPairs(ListNode* head) {
ListNode* dummyNode = new ListNode(0);
dummyNode -> next = head;
ListNode* cur = dummyNode;
//判断条件即为当前节点的下一个节点和下两个节点不为空
while(cur -> next != nullptr && cur -> next -> next != nullptr){
ListNode* tmp = cur -> next;
ListNode* tmp1 = cur -> next -> next -> next;
cur -> next = cur -> next -> next;//步骤1
cur -> next -> next = tmp;//步骤2
cur -> next -> next -> next = tmp1;//步骤3
cur = cur -> next -> next;//cur移动两位,准备下一轮交换
}
ListNode* result = dummyNode -> next;
delete dummyNode;//释放内存,避免内存泄漏
return result;
}
};——————————————————————————————分割线 2025.2.4
寒假回家磨磨唧唧基本没开始学习,今天俺老孙真的要开始学习啦!务必完成既定任务,2.28完成一刷代码随想录。
*5.【删除链表的倒数第n个结点】
思路:快慢指针,快指针走n+1步后,再和慢指针同时走,此时当快指针指向nullptr时,慢指针指向要删除的节点。
class Solution {
public:
ListNode* removeNthFromEnd(ListNode* head, int n) {
ListNode* dummyNode = new ListNode(0);
dummyNode -> next = head;
ListNode* fast = dummyNode;
ListNode* slow = dummyNode;
while(n-- && fast != nullptr){
fast = fast -> next;//fast走了n步
}
fast = fast -> next;//fast多走一步
while(fast != nullptr){
fast = fast -> next;
slow = slow -> next;
}
slow -> next = slow -> next ->next;//通过链表指向来删除节点
return dummyNode -> next;//不return head的原因是,有可能删除头节点
}
};
时间复杂度:O(n)
空间复杂度:O(1) 对比一下
6.【链表相交】
思路:遍历完自身之后,回到另一个链表的头节点。题目较为简单,但需注意细节
class Solution {
public:
ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) {
ListNode* PA = headA;
ListNode* PB = headB;
if(!headA || !headB){
return nullptr;
}
while(PA != PB){
PA = (PA == nullptr) ? headB : PA -> next;
PB = (PB == nullptr) ? headA : PB -> next;
}
return PA;
}
};*7.【环形链表Ⅱ】
思路:要进行两个判断,1.判断链表是否有环;2.如果有环,如何找到环的入口
对于1.可以用快慢指针来判断是否有环,快指针与慢指针相遇
class Solution {
public:
ListNode *detectCycle(ListNode *head) {
ListNode* fast = head;
ListNode* slow = head;
while(true){
if(fast == nullptr || fast -> next == nullptr) return nullptr;
fast = fast -> next -> next;
slow = slow -> next;
if(fast == slow) break;
}
fast = head;
while(slow != fast){
slow = slow -> next;
fast = fast -> next;
}
return fast;
}
};8.【两数相加】
class Solution {
public:
ListNode *addTwoNumbers(ListNode *l1, ListNode *l2) {
ListNode *head = nullptr, *tail = nullptr;//head:结果链表的头指针(最终返回),tail用于追踪当前链表的末尾,以便添加新节点
int carry = 0;//存储进位值
while(l1 || l2){ //只要l1和l2任意一个不为空
int n1 = l1 ? l1 -> val : 0; //如果l1存在,取出值
int n2 = l2 ? l2 -> val : 0;
int sum = n1 + n2 + carry;
//构建结果链表
if(!head){ //head为空说明是第一个节点
head = tail = new ListNode(sum % 10);//head和tail都指向同一个新创建的节点,后续可以正确添加新节点
}else{//否则创建新节点并连接到链表
tail -> next = new ListNode(sum % 10);
tail = tail -> next;
}
carry = sum / 10;
if(l1){
l1 = l1 -> next;
}
if(l2){
l2 = l2 -> next;
}
}
if(carry > 0){
tail -> next = new ListNode(carry);
}
return head;
}
};9.【合并两个有序链表】
思路:递归
class Solution {
public:
ListNode* mergeTwoLists(ListNode* list1, ListNode* list2) {
if(!list1) return list2;
if(!list2) return list1;
if(list1 -> val < list2 -> val){
list1 -> next = mergeTwoLists(list1 -> next, list2);
return list1;//哪个链表的头节点小,就返回哪个
}else{
list2 -> next = mergeTwoLists(list1, list2 -> next);
return list2;
}
}
};三、哈希表
1.有效的字母异位词
思路:先判断两个字符串长度是否相等,若相等再通过对哈希表的键值增减,最终如果哈希表中的所有键所对应的值都为0时,返回true。
class Solution {
public:
bool isAnagram(string s, string t) {
if(s.length() != t.length()) return false;
unordered_map<char, int> map;
for(char c : s){
map[c] += 1;
}
for(char c : t){
map[c] -= 1;
}
for(auto kv : map){ // kv 是键值对的意思
if(kv.second != 0) return false;
}
return true;
}
};2.两个数组的交集
思路:因为题目里有去重的要求,所以采用集合的方式;
在此辨析一下哈希表map、set和数组的异同

nums_set.find(num) != nums_set.end() 指find返回的迭代器不等于end(),说明num元素在nums_set中找到了。
class Solution {
public:
vector<int> intersection(vector<int>& nums1, vector<int>& nums2) {
unordered_set<int> result_set;
unordered_set<int> nums_set(nums1.begin(), nums1.end());
for(int num : nums2){
if(nums_set.find(num) != nums_set.end()){
result_set.insert(num);
}
}
return vector<int>(result_set.begin(), result_set.end());
}
};3.两数之和
思路:题目要求返回数组下标,所以不采用哈希表map、set
暴力解法,两个for循环:
class Solution {
public:
vector<int> twoSum(vector<int>& nums, int target) {
for(int i = 0; i < nums.size(); i++){
for(int j = i + 1; j < nums.size(); j++){
if(target - nums[i] == nums[j]){
return {i, j};
}
}
}
return {};
}
};采用哈希表map来解决,每遍历一个,查找一次其对应的目标值是否存在哈希表中,不存在,则加入该值,存在则返回这两个值的下标。
class Solution {
public:
vector<int> twoSum(vector<int>& nums, int target) {
unordered_map<int, int> nums_map;
for(int i = 0; i < nums.size(); i++){
if(nums_map.find(target - nums[i]) != nums_map.end()){
return {i, nums_map.find(target - nums[i])->second};
}else{
nums_map.insert(pair<int, int>(nums[i], i));
}
}
return {};
}
};*4.三数之和
思路(采用k神做法):1.先将数组排序;2.设三个指针,k为最左(最小)元素的指针,双指针i,j分别设在数组索引(k,len(nums))两端。双指针i,j交替向中间移动,记录满足题意的i,j,k组合。关键点在于,三个指针都要跳过重复值。
class Solution {
public:
vector<vector<int>> threeSum(vector<int>& nums) {
vector<vector<int>> res; //存储结果
if(nums.size() < 3) return res;
//先排序
sort(nums.begin(), nums.end());
//遍历每一个元素,作为第一个指针nums[k]
for(int k = 0; k < nums.size() - 2; k++){
//跳过重复的元素,避免重复组合
//k > 0的条件是为了避免跳过k=0这个元素
if(k > 0 && nums[k] == nums[k - 1]) continue;
int i = k + 1, j = nums.size() - 1;
while(i < j){
int sum = nums[k] + nums[i] + nums[j];
if(sum < 0){
//如果和小于0,i向右移动
i++;
//跳过重复的元素
while(i < j && nums[i] == nums[i - 1]) i++;
}else if(sum > 0){
//如果和大于0,j向左移动
j--;
//跳过重复的元素
while(i < j && nums[j] == nums[j + 1]) j--;
}else{
//sum == 0, 找到一个解
res.push_back({nums[k], nums[i], nums[j]});
i++;
j--;
//跳过重复的元素
while(i < j && nums[i] == nums[i - 1]) i++;
while(i < j && nums[j] == nums[j + 1]) j--;
}
}
}
return res;
}
};5.最长连续序列
unordered_set 会自动去重。这样,可以确保只有唯一的元素被存储。
思路:为了方便查找使用set哈希表存储数组,关键是找到连续子序列的起始位置,找到该位置之后向后寻找最长序列。
class Solution {
public:
int longestConsecutive(vector<int>& nums) {
if(nums.empty()) return 0;
unordered_set<int> numSet(nums.begin(), nums.end());
int longestStrak = 0;
for(int num : numSet){
//找到连续子序列的起点位置
if(numSet.find(num - 1) == numSet.end()){
int currentNum = num;
int streakNum = 1;
//向后寻找最长序列
while(numSet.find(currentNum + 1) != numSet.end()){
streakNum++;
currentNum++;
}
longestStrak = max(streakNum, longestStrak);
}
}
return longestStrak;
}
};四、字符串
1.反转字符串
思路:遇到反转题目,想双指针,比如之前做过的链表反转。
class Solution {
public:
void reverseString(vector<char>& s) {
int i = 0, j = s.size() - 1;
while(i < j){
char tmp = s[i];
s[i] = s[j];
s[j] = tmp;
i++;
j--;
}
}
};2.反转字符串Ⅱ
reverse(start_iterator,end_iterator)用法:start_iterator包含在内,而end_iterator不包含在内。
class Solution {
public:
string reverseStr(string s, int k) {
for(int i = 0; i < s.size(); i += 2*k){
if(i + k <= s.size()){
reverse(s.begin() + i, s.begin() + i + k);
}else{
reverse(s.begin() + i, s.end());
}
}
return s;
}
};3.替换数字
思路:很多数组填充类问题,都是先扩充数组到填充后的大小,然后再从后向前填充;这样做避免了两个问题:1.重新申请一个新数组;2.避免了从前向后填充时,需要将添加元素之后的所有元素向后移动的问题。
#include <iostream>
using namespace std;
int main() {
string s;
while (cin >> s) {
int sOldIndex = s.size() - 1;
int count = 0; // 统计数字的个数
for (int i = 0; i < s.size(); i++) {
if (s[i] >= '0' && s[i] <= '9') {
count++;
}
}
// 扩充字符串s的大小,也就是将每个数字替换成"number"之后的大小
s.resize(s.size() + count * 5);
int sNewIndex = s.size() - 1;
// 从后往前将数字替换为"number"
while (sOldIndex >= 0) {
if (s[sOldIndex] >= '0' && s[sOldIndex] <= '9') {
s[sNewIndex--] = 'r';
s[sNewIndex--] = 'e';
s[sNewIndex--] = 'b';
s[sNewIndex--] = 'm';
s[sNewIndex--] = 'u';
s[sNewIndex--] = 'n';
} else {
s[sNewIndex--] = s[sOldIndex];
}
sOldIndex--;
}
cout << s << endl;
}
}
*4.反转字符串中的单词
法一:双指针
思路(参考k神):1.倒序遍历字符串s,记录单词左右索引边界i,j;2.每确定一个单词的边界,则将其添加至单词列表res;3.最终将单词列表拼接成字符串,返回
class Solution {
public:
string reverseWords(string s) {
int n = s.size();
vector<string> res;
int i = n - 1;
while(i >= 0){
//跳过空格,寻找单词的结尾
//外层循环(i >= 0),是从右向左扫描字符串,直到遍历完整个字符串;内层循环(i >= 0)是为了防止越界。
while(i >= 0 && s[i] == ' '){
i--;
}
if(i < 0) break;
int j = i;//记录单词的结束位置
//找到单词的开始位置
while(i >= 0 && s[i] != ' '){
i--;
}
//提取单词,将其添加到结果列表
//substr的第二个参数表示字串的长度,而不是索引
res.push_back(s.substr(i+1, j-i));
}
//拼接字符串
string result;
for(int k = 0; k < res.size(); k++){
result += res[k];
if(k != res.size() - 1){
result += " ";
}
}
return result;
}
};五、栈与队列
1.理论基础
栈和队列是STL(C++标准库)里面的两个数据结构。
【相关C++八股】
1.C++中stack 是容器么?
答:不是,而是一种容器适配器。
2.我们使用的stack是属于哪个版本的STL?
答:SGI STL里面的数据结构。
3.我们使用的STL中stack是如何实现的?
答:如果没有指定底层实现的话,默认是以deque为缺省的情况下栈的底层结构。deque是一个双端队列,封住一端,开通另一端就实现栈的逻辑了。同理,队列底层实现在缺省的情况下也是deque。
【栈】
栈提供push 和 pop 等等接口,所有元素必须符合先进后出规则,所以栈不提供走访功能,也不提供迭代器(iterator)。 不像是set 或者map 提供迭代器iterator来遍历所有元素。
栈是以底层容器完成其所有的工作,对外提供统一的接口,底层容器是可插拔的(也就是说我们可以控制使用哪种容器来实现栈的功能)
所以STL中栈往往不被归类为容器,而被归类为container adapter(容器适配器)。
栈的内部结构,栈的底层实现可以是vector,deque,list 都是可以的, 主要就是数组和链表的底层实现。
我们常用的SGI STL,如果没有指定底层实现的话,默认是以deque为缺省情况下栈的底层结构。
【栈提供了以下基本操作】:
push( )-压栈;pop( )-弹栈;top( )-查看栈顶元素;empty( )-检查栈是否为空;size( )-获取栈的大小
【队列】
队列中先进先出的数据结构,同样不允许有遍历行为,不提供迭代器, SGI STL中队列一样是以deque为缺省情况下的底部结构。


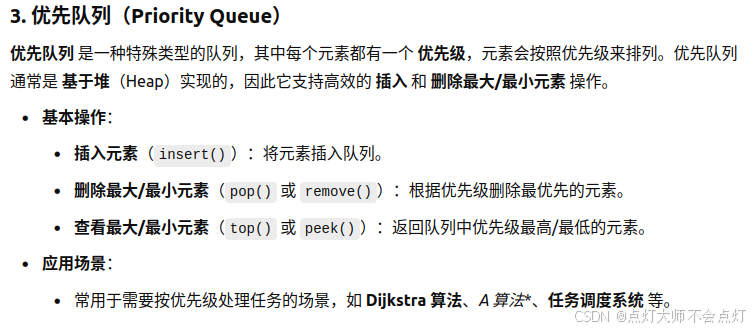
【堆】
针对上述优先级队列(披着队列外衣的堆),引出堆的概念。

三者的区别与联系:
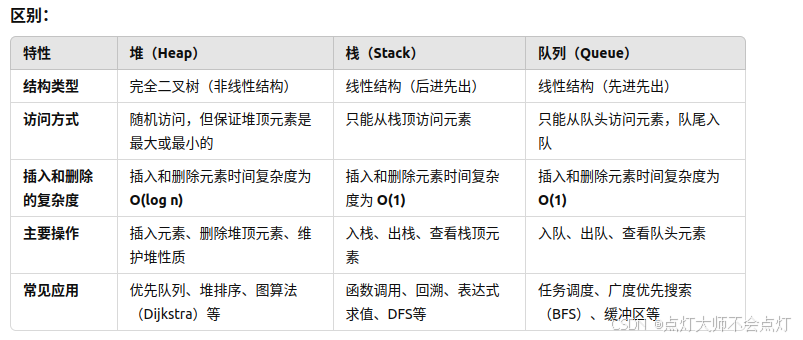

所以大家经常说的大顶堆(堆头是最大元素),小顶堆(堆头是最小元素),如果懒得自己实现的话,就直接用priority_queue(优先级队列)就可以了,底层实现都是一样的,从小到大排就是小顶堆,从大到小排就是大顶堆。
2.有效的括号
思路:1.如果s字符串个数为奇数,一定返回false;2.创建哈希表,把左右括号设为一组键值对,这里要注意哈希表赋初值,需要分号“;”结尾;3.括号匹配问题用栈来实现,所以创建栈;
class Solution {
public:
bool isValid(string s) {
int n = s.size();
if(n % 2 == 1){
return false;
}
unordered_map<char, char> pairs = {
{')', '('},
{']', '['},
{'}', '{'}
};
stack<char> stk;
for(char ch : s){
//pairs.count(ch)类似于find,只返回0或1
if(pairs.count(ch)){
if(stk.empty() || stk.top() != pairs[ch]){
return false;
}
//栈顶元素是正确的配对括号,所以出栈
stk.pop();
}else{
stk.push(ch);
}
}
return stk.empty();
}
};3.删除字符串中的所有相邻重复项
思路:和“有效的括号”本质一样,都是匹配问题,前者匹配括号,后者匹配相邻元素。
栈的目的就是来存放遍历过的元素,当遍历当前元素时,去栈里看看是否遍历过,然后再去消除。
class Solution {
public:
string removeDuplicates(string s) {
stack<char> stack;
string result = "";
for(int i = 0; i < s.length(); i++){
if(!stack.empty() && stack.top() == s[i]){
stack.pop();
}else{
stack.push(s[i]);
}
}
while(!stack.empty()){
result += stack.top();
stack.pop();
}
reverse(result.begin(), result.end());//记得翻转
return result;
}
};不使用显示的栈,直接利用字符串本身模拟栈:
class Solution {
public:
string removeDuplicates(string s) {
string result;
for(char c : s){
if(!result.empty() && result.back() == c){
result.pop_back();
}else{
result.push_back(c);
}
}
return result;
}
};*4.滑动窗口最大值
滑动窗口问题常用双端队列
算法流程(参照k神):
1.初始化:双端队列deque,结果列表res,数组长度n
2.滑动窗口:左边界范围i∈[1−k,n−k],右边界范围j∈[0,n−1];
a.若i>0且 队首元素deque[0] =被删除元素nums[i−1]:则队首元素出队;
b.删除deque内所有<nums[j]的元素,以保持deque递减;
c.将nums[j]添加至deque尾部;
d.若已形成窗口(即i≥0):将窗口最大值(即队首元素deque[0])添加至列表res;
3.返回值:返回结果列表res
class Solution {
public:
vector<int> maxSlidingWindow(vector<int>& nums, int k) {
if(nums.size() == 0 || k == 0) return{};
deque<int> deque;
vector<int> res(nums.size() - k + 1);//预先分配res数组大小
//i,j的初始值这样设置的目的是为了保证deque.back()一个一个进,从而使得队列是递减的
for(int i = 1 - k, j = 0; j < nums.size(); i++, j++){
//删除deque中对应的nums[i - 1]
if(i > 0 && deque.front() == nums[i - 1]){
deque.pop_front();
}
//保持deque递减
while(!deque.empty() && deque.back() < nums[j]){
deque.pop_back();
}
deque.push_back(nums[j]);
//记录窗口最大值
if(i >= 0){
res[i] = deque.front();
}
}
return res;
}
};5.前k个高频元素
算法流程(三步):
第一步:使用map哈希表统计频率;
*第二步:将频率进行排序
采用小顶堆,因为要统计最大前k个元素,只有小顶堆每次将最小的元素弹出,最后小顶堆里积累的才是前k个最大元素。
在 C++ 中,priority_queue 默认是 大顶堆,即堆顶元素是最大值,最小的元素会被保存在队列的底部。而在题目中,我们需要一个 小顶堆(min-heap),要求堆顶元素是 频率最小的元素,这样当堆大小超过 k 时,我们可以通过弹出堆顶元素来保证堆中始终存储的是前 k 个频率最高的元素。
为此,我们需要自定义一个 比较器,来修改 priority_queue 的默认排序方式,确保它按照频率的大小来组织堆中的元素。
class mycomparison {
public:
bool operator()(const pair<int, int>& lhs, const pair<int, int>& rhs) {
return lhs.second > rhs.second;
}
};
//定义小顶堆
priority_queue<pair<int, int>, vector<pair<int, int>>, mycomparison> pri_que;通过使用比较器来实现 小顶堆 或其他排序规则。
priority_queue 需要三个参数来指定:
元素类型(pair<int, int>)。
底层容器类型(通常是 vector<T>)。
比较器(用于指定堆中元素的排序规则)。
pair<int, int>:- 这是优先队列中元素的类型。因为我们存储的是
pair<int, int>类型的元素,其中第一个int表示数字,第二个int表示该数字的出现次数(频率)。在这个例子中,队列的每个元素是一个pair<int, int>,例如(数字, 频率)。
- 这是优先队列中元素的类型。因为我们存储的是
-
vector<pair<int, int>>:- 这是底层容器类型。
priority_queue在内部通常使用一个 动态数组(通常是vector)来存储元素。这里,vector<pair<int, int>>表示我们使用vector来存储pair<int, int>类型的元素。你也可以使用其他容器,如deque,但通常vector是最常用的选择,因为它可以高效地动态扩展大小。
- 这是底层容器类型。
-
mycomparison:- 这是一个自定义的比较器。
priority_queue默认是一个大顶堆(大元素排在堆顶),但是在这里,我们需要一个小顶堆(小元素排在堆顶)。通过传递自定义的比较器mycomparison,我们告诉priority_queue如何排序堆中的元素。mycomparison是一个类,它重载了operator()来定义元素的排序规则。在这个例子中,mycomparison会使得优先队列根据pair的第二个元素(即频率)来排序。
- 这是一个自定义的比较器。
要遍历 unordered_map 中的所有元素,我们需要使用 迭代器。iterator 是指向容器中某个元素的指针,可以通过它来访问容器中的每个元素。:: 是在声明迭代器类型时使用。
unordered_map<int, int>::iterator it = map.begin();
这个部分是用来定义一个迭代器(iterator),并将它初始化为 unordered_map 的开始位置。
for (unordered_map<int, int>::iterator it = map.begin(); it != map.end(); it++) {
pri_que.push(*it); // 将每个元素(数字和频率)插入到优先队列中
if (pri_que.size() > k) { // 如果堆的大小超过了k
pri_que.pop(); // 弹出堆顶元素(频率最小的元素)
}
}
插入时,mycomparison 比较器 会被调用。这个比较器会根据 频率 排序,因此优先队列会保持一个 小顶堆(堆顶元素是频率最小的元素)。
第三步:找出前k个高频元素
构建小堆顶,将所有频率入堆,如果堆的大小大于k了,将元素从堆顶弹出
class Solution {
public:
// 小顶堆
class mycomparison {
public:
bool operator()(const pair<int, int>& lhs, const pair<int, int>& rhs) {
return lhs.second > rhs.second;
}
};
vector<int> topKFrequent(vector<int>& nums, int k) {
// 要统计元素出现频率
unordered_map<int, int> map; // map<nums[i],对应出现的次数>
for (int i = 0; i < nums.size(); i++) {
map[nums[i]]++;
}
// 对频率排序
// 定义一个小顶堆,大小为k
priority_queue<pair<int, int>, vector<pair<int, int>>, mycomparison> pri_que;
// 用固定大小为k的小顶堆,扫面所有频率的数值
for (unordered_map<int, int>::iterator it = map.begin(); it != map.end(); it++) {
pri_que.push(*it);
if (pri_que.size() > k) { // 如果堆的大小大于了K,则队列弹出,保证堆的大小一直为k
pri_que.pop();
}
}
// 找出前K个高频元素,因为小顶堆先弹出的是最小的,所以倒序来输出到数组
vector<int> result(k);
for (int i = k - 1; i >= 0; i--) {
result[i] = pri_que.top().first;
pri_que.pop();
}
return result;
}
};
6.用栈实现队列
思路:需要两个栈,一个输入、一个输出。
六、二叉树
1.理论基础
二叉树题目分类

【二叉树的种类】
- 满二叉树:一颗二叉树只有度为0的节点和度为2的节点,并且度为0的节点在同一层。深度为k,有2^k-1个节点的二叉树。
- 完全二叉树:除了最底层节点可能没被填满,其余每层节点数都达到最大值,并且最下面一层的节点都集中在该层最左边的若干位置。
- 二叉搜索树:一个有序数。左子树小于根节点值,右子数大于根节点值。
- 平衡二叉搜索树:是一颗空树或者它的左右两个子树的高度差的绝对值不超过1,并且左右两个子树都是一颗平衡二叉树。
【二叉树的存储方式】
链式存储:指针。通过指针把分布在各个地址的节点串连在一起。
顺序存储:数组。内存连续分布。
【二叉树的遍历方式】
1.深度优先遍历:先往深走,遇到叶子节点再往回走。
借助栈使用递归的方式来实现。
- 前序遍历(递归法,迭代法)
- 中序遍历(递归法,迭代法)
- 后序遍历(递归法,迭代法) 这里的“前中后”指的是中间节点的位置
2.广度优先遍历:一层一层的去遍历。
借助队列先进先出的特点来实现。
- 层次遍历(迭代法)
【二叉树的定义】
顺序存储即是用数组来存,这里主要讨论链式存储的二叉树节点的定义方式。
struct TreeNode {
int val;
TreeNode *left;
TreeNode *right;
TreeNode(int x) : val(x), left(NULL), right(NULL) {}
};
在此,对比一下链表定义,相对于链表,二叉树节点里多了一个指针
struct ListNode{
int val;//节点上存储的元素
ListNode *next;//指向下一节点的指针
ListNode(int x) : val(x), next(NULL) {}//节点的构造函数
};2.二叉树的递归遍历
递归三要素:
1>确定递归函数的参数和返回值;
2>确定终止条件;操作系统用一个栈的结构来保存每一层递归的信息,如果递归没有终止,操作系统的内存栈必然会溢出。
3>确定单层递归的逻辑
例:前序遍历
class Solution {
public:
void travelsal(TreeNode* cur, vector<int>& vec){
if(cur == NULL) return;
vec.push_back(cur -> val);
travelsal(cur -> left, vec);
travelsal(cur -> right, vec);
}
vector<int> preorderTraversal(TreeNode* root) {
vector<int> res;
travelsal(root, res);
return res;
}
};3.二叉树的层序遍历
广度优先搜索(BFS)通常借助队列的先入先出特性来实现。
算法流程:
1.特例处理:当根节点为空,返回空列表[ ];
2.初始化:打印结果列表res = [ ],包含根节点的队列 queue = [root]。
3.BFS循环:queue为空时跳出
a.临时列表tmp,存储当前层打印结果
b.当前层打印循环:循环次数为当前节点数(queue长度)
c.将当前层结果tmp添加入res。
4.返回值:返回打印结果res
class Solution {
public:
vector<vector<int>> levelOrder(TreeNode* root) {
queue<TreeNode*> que;
vector<vector<int>> res;
if(root != nullptr) que.push(root);//先把根节点入队
while(!que.empty()){
vector<int> tmp;//存储当前层的节点值
for (int i = que.size(); i > 0; i--) {//遍历当前层的所有节点
Treenode* node = que.front();// 获取队列的第一个节点
que.pop(); // 弹出队列的第一个节点
tmp.push_back(node->val); // 将当前节点的值添加到当前层的结果中
if (node->left != nullptr) que.push(node->left); // 如果有左子树,入队
if (node->right != nullptr) que.push(node->right);// 如果有右子树,入队
}
res.push_back(tmp);
}
return res;
}
};【二叉树的最大深度】
vector 可以临时存储当前层节点,在每一层遍历结束后,可以直接更新 que。它不需要像 queue 那样每次进行 pop() 操作,这样代码更加简洁和直接。
class Solution {
public:
int maxDepth(TreeNode* root) {
if(root == nullptr) return 0;
vector<TreeNode*> que;
que.push_back(root);
int res = 0;
while(!que.empty()){
vector<TreeNode*> tmp;
for(TreeNode* node : que){
if(node -> left != nullptr) tmp.push_back(node -> left);
if(node -> right != nullptr) tmp.push_back(node -> right);
}
que = tmp;//由tmp更新que
res++;
}
return res;
}
};【二叉树的右视图】
思路:和层序遍历的逻辑类似,只需要判断当前指针是否是该层的最后一个元素,是的话放进result数组。
class Solution {
public:
vector<int> rightSideView(TreeNode* root) {
queue<TreeNode*> que;
if(root != nullptr) que.push(root);
vector<int> result;
while(!que.empty()){
int size = que.size();
for(int i = 0; i < size; i++){
TreeNode* node = que.front();
que.pop();
if(i == (size - 1)) result.push_back(node -> val);
if(node -> left) que.push(node -> left);
if(node -> right) que.push(node -> right);
}
}
return result;
}
};4.【翻转二叉树】
思路:交换每一个节点的左右孩子。
class Solution {
public:
TreeNode* invertTree(TreeNode* root) {
if(root == nullptr) return root;
swap(root -> left, root -> right);
invertTree(root -> left);
invertTree(root -> right);
return root;
}
};5.【对称二叉树】
递归法
递归三要素:1.递归函数的参数和返回值
因为要判断的是这个数是否是对称的,所以参数是左子树和右子树节点,返回值是bool类型
bool compare(Treenode* left, Treenode* right)2.确定终止条件
if (left == NULL && right != NULL) return false;
else if (left != NULL && right == NULL) return false;
else if (left == NULL && right == NULL) return true;
else if (left->val != right->val) return false; // 注意这里我没有使用else
3.确定单层递归的逻辑
单层递归的逻辑就是处理左右节点都不为空,且数值相同的情况。
- 比较二叉树外侧是否对称:传入的是左节点的左孩子,右节点的右孩子。
- 比较内侧是否对称,传入左节点的右孩子,右节点的左孩子。
- 如果左右都对称就返回true ,有一侧不对称就返回false 。
bool outside = compare(left->left, right->right); // 左子树:左、 右子树:右
bool inside = compare(left->right, right->left); // 左子树:右、 右子树:左
bool isSame = outside && inside; // 左子树:中、 右子树:中(逻辑处理)
return isSame;
最终代码:
class Solution {
public:
bool compare(TreeNode* left, TreeNode* right) {
// 首先排除空节点的情况
if (left == NULL && right != NULL) return false;
else if (left != NULL && right == NULL) return false;
else if (left == NULL && right == NULL) return true;
// 排除了空节点,再排除数值不相同的情况
else if (left->val != right->val) return false;
// 此时就是:左右节点都不为空,且数值相同的情况
// 此时才做递归,做下一层的判断
bool outside = compare(left->left, right->right); // 左子树:左、 右子树:右
bool inside = compare(left->right, right->left); // 左子树:右、 右子树:左
bool isSame = outside && inside; // 左子树:中、 右子树:中 (逻辑处理)
return isSame;
}
bool isSymmetric(TreeNode* root) {
if (root == NULL) return true;
return compare(root->left, root->right);
}
};
6.【完全二叉树节点个数】
方法一:对层序遍历的模板稍作修改,统计节点个数。
class Solution {
public:
int countNodes(TreeNode* root) {
queue<TreeNode*> que;
if(root != nullptr) que.push(root);
int count = 0;
while(!que.empty()){
int size = que.size();
for(int i = 0; i < size; i++){
TreeNode* node = que.front();
que.pop();
count++;
if(node -> left) que.push(node -> left);
if(node -> right) que.push(node -> right);
}
}
return count;
}
};方法二:递归
确定返回参数和终止条件,确定递归逻辑,最终代码:
class Solution {
public:
int getCount(TreeNode* cur){
if(cur == nullptr) return 0;
int leftNum = getCount(cur -> left);
int rightNum = getCount(cur -> right);
int count = leftNum + rightNum + 1;
return count;
}
int countNodes(TreeNode* root) {
if(root == nullptr) return 0;
return getCount(root);
}
};7.平衡二叉树
class Solution {
public:
//如果返回-1 则说明该节点不是平衡二叉树
int balanced(TreeNode* cur){
//如果当前根节点为空,则表示当前根节点的树高度为0
if(cur == nullptr) return 0;
int leftHeight = balanced(cur -> left);
if(leftHeight == -1) return -1;
int rightHeight = balanced(cur -> right);
if(rightHeight == -1) return -1;
//+1的原因是加上当前根节点
return abs(leftHeight - rightHeight) > 1 ? -1 : 1 + max(leftHeight, rightHeight);
}
bool isBalanced(TreeNode* root) {
return balanced(root) == -1 ? false : true;
}
};8.二叉树的所有路径
思路:递归+回溯,回溯的原因:返回上一步根节点,继续遍历。
递归参数:节点值、遍历过的路径、存放结果集的result
返回类型:此处递归,不需要返回值
递归终止条件:
if(cur == nullptr){
//处理递归逻辑
}通用递归结束条件可以这么写,但是本题递归条件应为,判断是否为叶子节点,为啥不用判断当前节点是否为空,因为后续逻辑能够使得空节点不入循环。
这里介绍一个函数to_string(),它是C++ 标准库中的一个函数,定义在 <string> 头文件中。它是从 C++11 标准开始引入的,用于将数值类型(如 int、double、long 等)转换为string 类型。
开始动手写递归逻辑:
1.利用vector<int>的path容器,记录路径,则终止处理逻辑如下:
void versal(TreeNode* cur, vector<int>& path, vector<string>& result){
path.push_back(cur -> val);
if(cur -> left == nullptr && cur -> right == nullptr){
string spath;
//这里减1的原因是,最后一个path不需要箭头连接,所以单独处理
for(int i = 0; i < path.size() - 1; i++){
spath += to_string(path[i]);
spath += "->";
}
spath += to_string(path[path.size() - 1]);//记录最后一个节点(叶子节点)
result.push_back(spath);
return;
}
}处理完叶子节点之后,回溯到上一个节点,这里明确一点,一个递归对应一个回溯。
if(cur -> left){
versal(cur -> left, path, result);
path.pop_back();
}
if(cur -> right){
versal(cur -> right, path, result);
path.pop_back();
}整体代码:
class Solution {
public:
void versal(TreeNode* cur, vector<int>& path, vector<string>& result){
path.push_back(cur -> val);
if(cur -> left == nullptr && cur -> right == nullptr){
string spath;
//这里减1的原因是,最后一个path不需要箭头连接,所以单独处理
for(int i = 0; i < path.size() - 1; i++){
spath += to_string(path[i]);
spath += "->";
}
spath += to_string(path[path.size() - 1]);//记录最后一个节点(叶子节点)
result.push_back(spath);
return;
}
if(cur -> left){
versal(cur -> left, path, result);
path.pop_back();
}
if(cur -> right){
versal(cur -> right, path, result);
path.pop_back();
}
}
vector<string> binaryTreePaths(TreeNode* root) {
vector<string> result;
vector<int> path;
if(root == nullptr) return result;
versal(root, path, result);
return result;
}
};9.左叶子之和
class Solution {
public:
int traversal(TreeNode* cur){
if(cur == nullptr) return 0;
//递归终止条件,递归逻辑
if(cur -> left && !cur -> left -> left && !cur -> left -> right){
return cur -> left -> val + traversal(cur -> right);
}
int leftVal = traversal(cur -> left);
int rightVal = traversal(cur -> right);
return leftVal + rightVal;
}
int sumOfLeftLeaves(TreeNode* root) {
return traversal(root);
}
};10.找树左下角的值
思路:层序遍历,输出最后一层第一个元素。此外,做了很多关于层序遍历的题目后,发现根据输出的值不同,往往做变化的都是que.pop()这一句之后。
class Solution {
public:
int findBottomLeftValue(TreeNode* root) {
queue<TreeNode*> que;
if(root) que.push(root);
int res = 0;
while(!que.empty()){
int size = que.size();
vector<int> tmp;
for(int i = 0; i < size; i++){
TreeNode* node = que.front();
que.pop();
if(i == 0) res = node -> val;
if(node -> left) que.push(node -> left);
if(node -> right) que.push(node -> right);
}
}
return res;
}
};七、回溯
递归和回溯的区别:
递归即是自己调用自己,回溯是枚举所有的可能,不满足条件的时候,撤销选择。
回溯是一个算法思想,递归是一种实现方式
回溯三部曲:
1.回溯返回值以及参数,返回值一般是void,参数很难一次性确定,所以一般先写逻辑,然后需要什么参数写什么。
2.回溯函数终止条件。
3.回溯搜索的遍历过程:回溯法一般是在集合中递归搜索,集合的大小构成了树的宽度,递归的深度构成树的深度。
回溯算法模板框架
void backtracking(参数) {
if (终止条件) {
存放结果;
return;
}
for (选择:本层集合中元素(树中节点孩子的数量就是集合的大小)) {
处理节点;
backtracking(路径,选择列表); // 递归
回溯,撤销处理结果
}
}
1.组合问题
思路:组合问题可抽象为树形结构

可以看出,这棵树一开始集合是1,2,3,4,从左向右取数,取过的数,不再重复取。
n相当于树的宽度,k相当于树的深度。
因此在这棵树上遍历从而收集我们要的结果:每次搜索到了叶子节点,就找到了一个结果。
class Solution {
private:
vector<vector<int>> result;//用来存放结果
vector<int> tmp;//用来存放符合条件的结果
void backTracking(int n, int k, int startIndex){
//for循环每次从startIndex开始
//回溯终止条件
if(tmp.size() == k){
result.push_back(tmp);
return;
}
for(int i = startIndex; i <= n; i++){
tmp.push_back(i);//处理结点
backTracking(n, k, i + 1);//递归
tmp.pop_back();//撤销处理的节点
}
}
public:
vector<vector<int>> combine(int n, int k) {
backTracking(n, k, 1);
return result;
}
};2.组合总和三
class Solution {
private:
vector<vector<int>> result;
vector<int> tmp;
void backTracking(int k, int targetSum, int startIndex, int curSum){
if(tmp.size() == k){
if(curSum == targetSum) result.push_back(tmp);
if(tmp.size() == k) 但是curSum != targetSum 直接返回
return;
}
for(int i = startIndex; i <= 9; i++){
curSum += i;
tmp.push_back(i);
backTracking(k, targetSum, i + 1, curSum);
curSum -= i;
tmp.pop_back();
}
}
public:
vector<vector<int>> combinationSum3(int k, int n) {
backTracking(k, n, 1, 0);
return result;
}
};3.子集
思路:

class Solution {
//基于数组的索引,因而startIndex是从0开始的
private:
vector<vector<int>> result;
vector<int> tmp;
void backTracking(vector<int>& nums, int startIndex){
result.push_back(tmp);
//终止条件为,startIndex的长度已经大于数组了,所以不用写,因为此时本层for循环,本来也结束了
for(int i = startIndex; i < nums.size(); i++){
tmp.push_back(nums[i]);
backTracking(nums, i + 1);
tmp.pop_back();
}
}
public:
vector<vector<int>> subsets(vector<int>& nums) {
backTracking(nums, 0);
return result;
}
};4.全排列
class Solution {
public:
vector<vector<int>> result;
vector<vector<int>> permute(vector<int>& nums) {
dfs(nums, 0);
return result;
}
void dfs(vector<int>& nums, int x){
if(x == nums.size() - 1){//递归终止条件
result.push_back(nums);//存储排列结果
return;
}
for(int i = x; i < nums.size(); i++){
swap(nums[i], nums[x]);//选择:交换元素
dfs(nums, x + 1);//递归:固定当前元素,排列剩下的
swap(nums[i], nums[x]);//回溯:撤销选择,恢复数组
}
}
};八、贪心算法
1.贪心算法理论基础
贪心算法一般分为如下四步:
1.将问题分解为若干个子问题;
2.找出适合的贪心策略;
3.求解每一个问题的最优解;
4.将局部最优解堆叠成全局最优解。
实际做题,只要能够由局部最优推导出全局最优,就够用。
2.分发饼干
思路:该题局部最优就是大饼干喂给胃口大的,全局最优就是喂饱尽可能多的小孩。尝试使用贪心策略,先将饼干数组和小孩数组进行排序,然后从后向前遍历小孩数组,用大饼干优先满足胃口大的,并统计满足小孩数量。
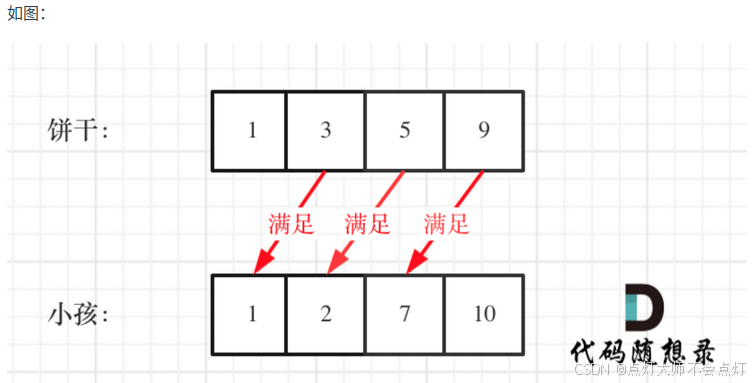
class Solution {
public:
int findContentChildren(vector<int>& g, vector<int>& s) {
sort(g.begin(), g.end());
sort(s.begin(), s.end());
int result = 0;
int sIndex = s.size() - 1;//饼干数组下标
//遍历小孩数组
for(int i = g.size() - 1; i >= 0; i--){
if(sIndex >= 0 && s[sIndex] >= g[i] ){
result++;
sIndex--;
}
}
return result;
}
};3.摆动序列
思路:看完答案感觉还挺简单,逻辑就是,当数组长度小于等于1的时候直接返回数组长度,其余条件就是判断是否前向差值和后向差值相反。
class Solution {
public:
int wiggleMaxLength(vector<int>& nums) {
if (nums.size() <= 1) return nums.size();
int curDiff = 0; // 当前一对差值
int preDiff = 0; // 前一对差值
int result = 1; // 记录峰值个数,序列默认序列最右边有一个峰值
for (int i = 0; i < nums.size() - 1; i++) {
curDiff = nums[i + 1] - nums[i];
// 出现峰值
if ((preDiff <= 0 && curDiff > 0) || (preDiff >= 0 && curDiff < 0)) {
result++;
preDiff = curDiff; // 注意这里,只在摆动变化的时候更新prediff
}
}
return result;
}
};4.买卖股票的最佳时机 2
注意:想要获得利润,至少两天为一个交易单元。
思路:看完解析,这题真的又好简单,我又懂了。
就是统计所有正利润之和。即,局部最优:收集每天的正利润;全局最优:求得最大利润。
class Solution {
public:
int maxProfit(vector<int>& prices) {
int result = 0;
for(int i = 1; i < prices.size(); i++){
if(prices[i] - prices[i - 1] > 0){
result += prices[i] - prices[i - 1];
}
}
return result;
}
};5.跳跃游戏
思路:局部最优解:每次取最大跳跃步数;整体最优解:是否能到达终点。
class Solution {
public:
bool canJump(vector<int>& nums) {
if(nums.size() <= 1) return true;
int cover = 0;
for(int i = 0; i <= cover; i++){
cover = max(nums[i] + i, cover);
if(cover >= nums.size() - 1) return true;
}
return false;
}
};6.跳跃游戏2
没看答案,自己的思路:从后向前遍历,先找到能跳跃到最后一个元素的下标,在该下标的基础上再去寻找能跳跃到此下标的下标。
发现自己的思路有问题,从后向前遍历的话,可能先遇到了一个能跳到最后一个元素的下标,但是该下标没有元素能跳过来。
class Solution {
public:
int jump(vector<int>& nums) {
int curDistance = 0; // 当前覆盖的最远距离下标
int ans = 0; // 记录走的最大步数
int nextDistance = 0; // 下一步覆盖的最远距离下标
for (int i = 0; i < nums.size() - 1; i++) { // 注意这里是小于nums.size() - 1,这是关键所在
nextDistance = max(nums[i] + i, nextDistance); // 更新下一步覆盖的最远距离下标
if (i == curDistance) { // 遇到当前覆盖的最远距离下标
curDistance = nextDistance; // 更新当前覆盖的最远距离下标
ans++;
}
}
return ans;
}
};7.K次取反后最大化的数组和
思路:局部最优:让绝对值大的负数变为正数;整体最优:整个数组和达到最大。
特殊情况:负数都转变为正数了,k依然大于0,此时的问题是一个有序正整数序列,如何转变k次正负,让数组和达到最大
算法步骤:1.将数组按照绝对值大小从大到小进行排序;
2.从前向后遍历,遇到负数将其变为正数,同时k--;
3.如果k依旧大于0, 反复转变数值最小的元素,将k用完;
4.求和
class Solution {
static bool cmp(int a, int b){
return abs(a) > abs(b);
}
public:
int largestSumAfterKNegations(vector<int>& nums, int k) {
int sum = 0;
//1.按照绝对值大小排序,从大到小
sort(nums.begin(), nums.end(), cmp);
//2.从前向后遍历,遇到负数则将其变为正数,同时k--
for(int i = 0; i < nums.size(); i++){
if(nums[i] < 0 && k > 0){
nums[i] = -nums[i];
k--;
}
}
//3.如果k依旧大于0
if(k > 0){
int n = nums.size() - 1;
if(k % 2 == 1){
nums[n] = -nums[n];
}
}
//4.求和
for(int i = 0; i < nums.size(); i++){
sum += nums[i];
}
return sum;
}
};九、动态规划
1.动态规划理论基础
动态规划(Dynamic Programming,简称DP),如果某一问题有很多重叠子问题,使用动态规划是最有效的。
动态规划中每一个状态一定是由上一个状态推导出来的。有别于贪心:局部直接选最优。
动态规划解题步骤(五步):
1.确定dp数组(dp table)以及下标的含义
2.确定递推公式
3.dp数组如何初始化
4.确定遍历顺序
5.举例推导dp数组
debug过程:
1.模拟状态转移在dp数组上的情况;
2.如果代码没通过,打印dp数组,看看和自己预先推导的哪里不一样;
3.如果预先模拟一样,就是递归公式、初始化、遍历顺序的问题。否则,代码实现细节问题。
2.斐波那契数
暴力解法
class Solution {
public:
int fib(int n) {
vector<int> nums(n+1);
if(n <= 1) return n;
nums[0] = 0, nums[1] = 1;
for(int i = 2; i <= n; i++){
nums[i] = nums[i - 1] + nums[i - 2];
}
return nums[n];
}
};























 1746
1746

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








