数字图像处理—7频域增强-优快云博客

本文链接：https://blog.youkuaiyun.com/2401_83669361/article/details/147439472

7.1 平滑滤波

平滑滤波使用的都是低通滤波器，包括理想低通滤波器、巴特沃斯低通滤波器、指数低通滤波器和梯形低通滤波器。在这里我们讲解理想低通滤波。对于理想低通滤波，我们需要了解以下代码：

①D0 = 30：

定义理想低通滤波器的截止频率 D0 为 30。截止频率决定了滤波器允许通过的频率范围，低于这个频率的成分将被保留，高于这个频率的成分将被衰减或去除。

②H = np.zeros(img.shape)：

创建一个与原图像 img 大小相同的全零数组 H，用于存储理想低通滤波器的传递函数。传递函数描述了滤波器对不同频率成分的响应。

③w, h = img.shape[0] // 2, img.shape[1] // 2：

img.shape[0]代表图像的高度，即图像垂直方向上的像素行数。img.shape[1]表示宽度。这行代码用于计算图像的中心坐标 w 和 h。这是为了在后续构建滤波器时，以图像中心为基准来确定每个像素点的频率。

④for i in range(img.shape[0]):

for j in range(img.shape[1]):

用于遍历图像的每个像素点。

⑤if (np.sqrt((i - w) ** 2 + (j - h) ** 2)) <= D0:

H[i, j] = 1

else:

H[i, j] = 0

因为我们已经对频谱进行了中心化，低频部分全部在图像中心。对于每个像素点 (i, j)，我们只需要计算其到图像中心的距离，便可以大致判断该点为低频还是高频。如果距离小于等于截止频率D0，则将滤波器传递函数H中对应位置的值设为1，表示该频率成分可以通过滤波器；否则设为0，表示该频率成分将被滤波器阻挡，不可通过。这样就构建了一个理想低通滤波器的传递函数H。

⑥img_f[:, :, 0] = img_f[:, :, 0] * H

img_f[:, :, 1] = img_f[:, :, 1] * H

分别将频域图像 img_f 的实部和虚部（第三个参数索引0对应实部，索引1对应虚部）与滤波器传递函数H相乘，以实现对频域图像的滤波操作，保留低频部分，去除高频部分。

⑦img_n = cv2.magnitude(img_n[:, :, 0], img_n[:, :, 1])：

cv2.magnitude 函数用于计算复数的幅值。由于逆离散傅里叶变换的结果是复数，通过这个函数计算实部和虚部的幅值，得到最终的滤波后图像 img_n。

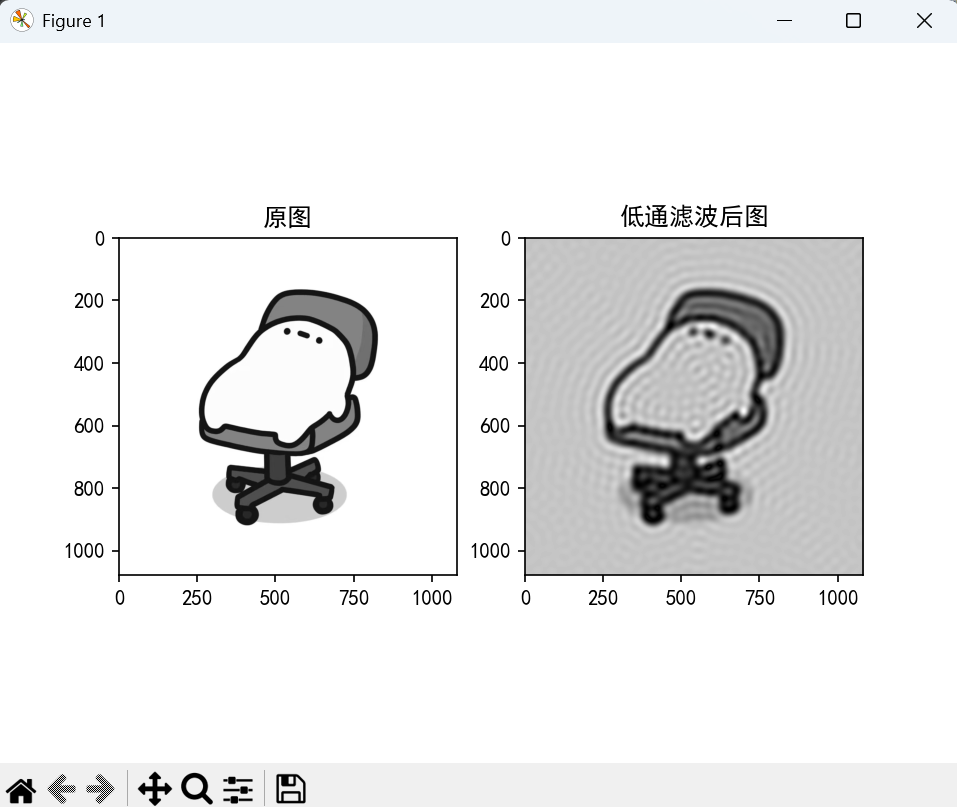
代码如下及运行结果如图3.27。

import cv2
import numpy as np
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
img = cv2.imread('001.bmp', 0)
img_f = cv2.dft(img / 255, flags=cv2.DFT_COMPLEX_OUTPUT)
img_f = np.fft.fftshift(img_f)
D0 = 30
H = np.zeros(img.shape)
w, h = img.shape[0] // 2, img.shape[1] // 2
for i in range(img.shape[0]):
    for j in range(img.shape[1]):
        if (np.sqrt((i - w) ** 2 + (j - h) ** 2)) <= D0:
            H[i, j] = 1
        else:
            H[i, j] = 0
img_f[:, :, 0] = img_f[:, :, 0] * H
img_f[:, :, 1] = img_f[:, :, 1] * H
img_f = np.fft.ifftshift(img_f)
img_n = cv2.idft(img_f)
img_n = cv2.magnitude(img_n[:, :, 0], img_n[:, :, 1])
plt.subplot(121)
plt.imshow(img, 'gray')
plt.title('原图')
plt.subplot(122)
plt.imshow(img_n, 'gray')
plt.title('低通滤波后图')
plt.show()

7.2 锐化滤波

锐化滤波使用的都是高通滤波器，包括理想高通滤波器、巴特沃斯高通滤波器、指数高通滤波器和梯形高通滤波器。在这里我们讲解理想高通滤波。

对于理想高通滤波器的代码，和理想低通滤波类似，只需要增大截止频率，并且保留大于截止频率的部分即可。

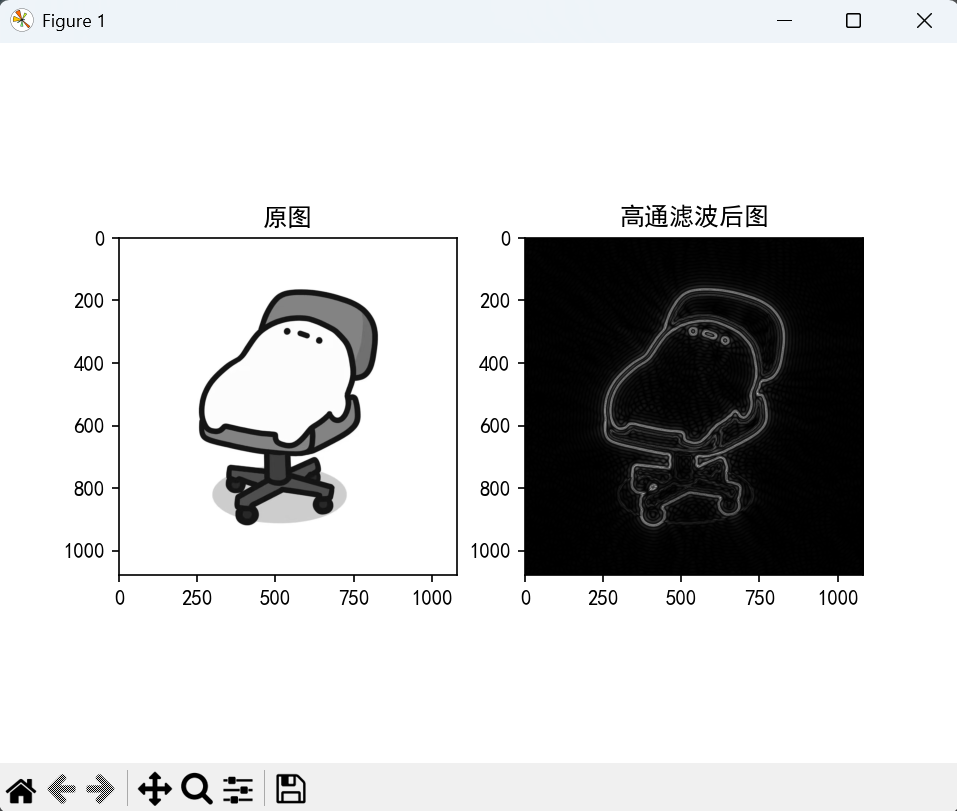
代码如下及运行结果如图3.28。

import cv2
import numpy as np
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
img = cv2.imread('001.bmp', 0)
img_f = cv2.dft(img / 255, flags=cv2.DFT_COMPLEX_OUTPUT)
img_f = np.fft.fftshift(img_f)
D0 = 50
H = np.zeros(img.shape)
w, h = img.shape[0] // 2, img.shape[1] // 2
for i in range(img.shape[0]):
    for j in range(img.shape[1]):
        if (np.sqrt((i - w) ** 2 + (j - h) ** 2)) <= D0:
            H[i, j] = 0
        else:
            H[i, j] = 1
img_f[:, :, 0] = img_f[:, :, 0] * H
img_f[:, :, 1] = img_f[:, :, 1] * H
img_f = np.fft.ifftshift(img_f)
img_n = cv2.idft(img_f)
img_n = cv2.magnitude(img_n[:, :, 0], img_n[:, :, 1])
plt.subplot(121)
plt.imshow(img, 'gray')
plt.title('原图')
plt.subplot(122)
plt.imshow(img_n, 'gray')
plt.title('高通滤波后图')
plt.show()