2025-11-20[归并排序、快乐数]

题目链接

归并排序

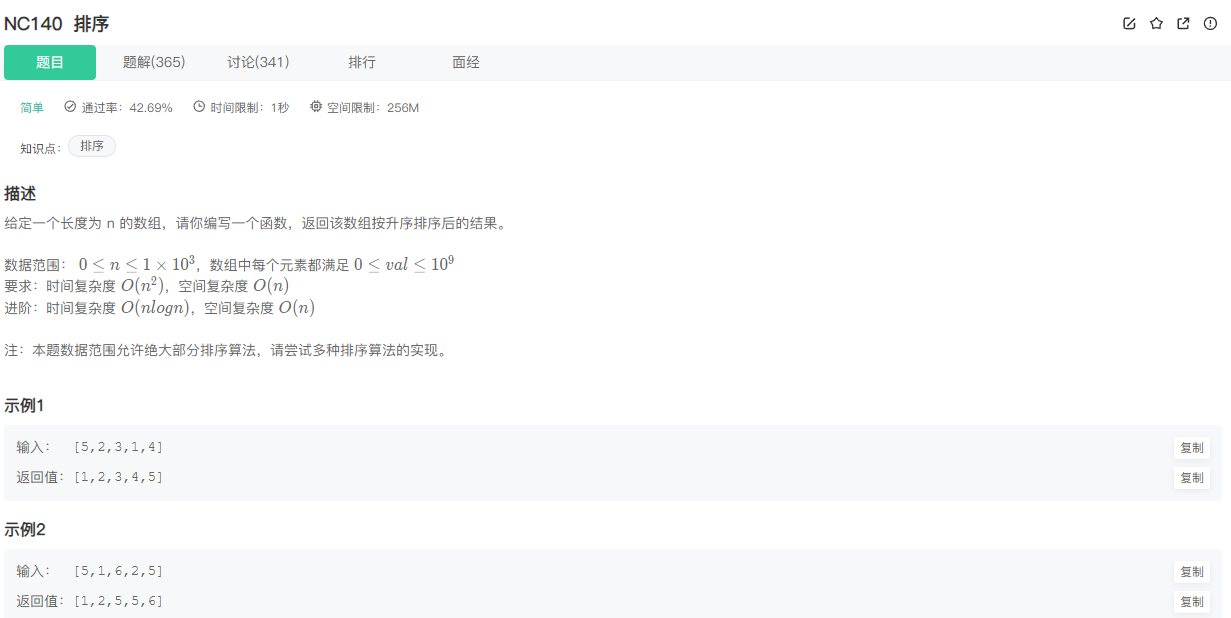
题目描述

题目解析

总体功能概述

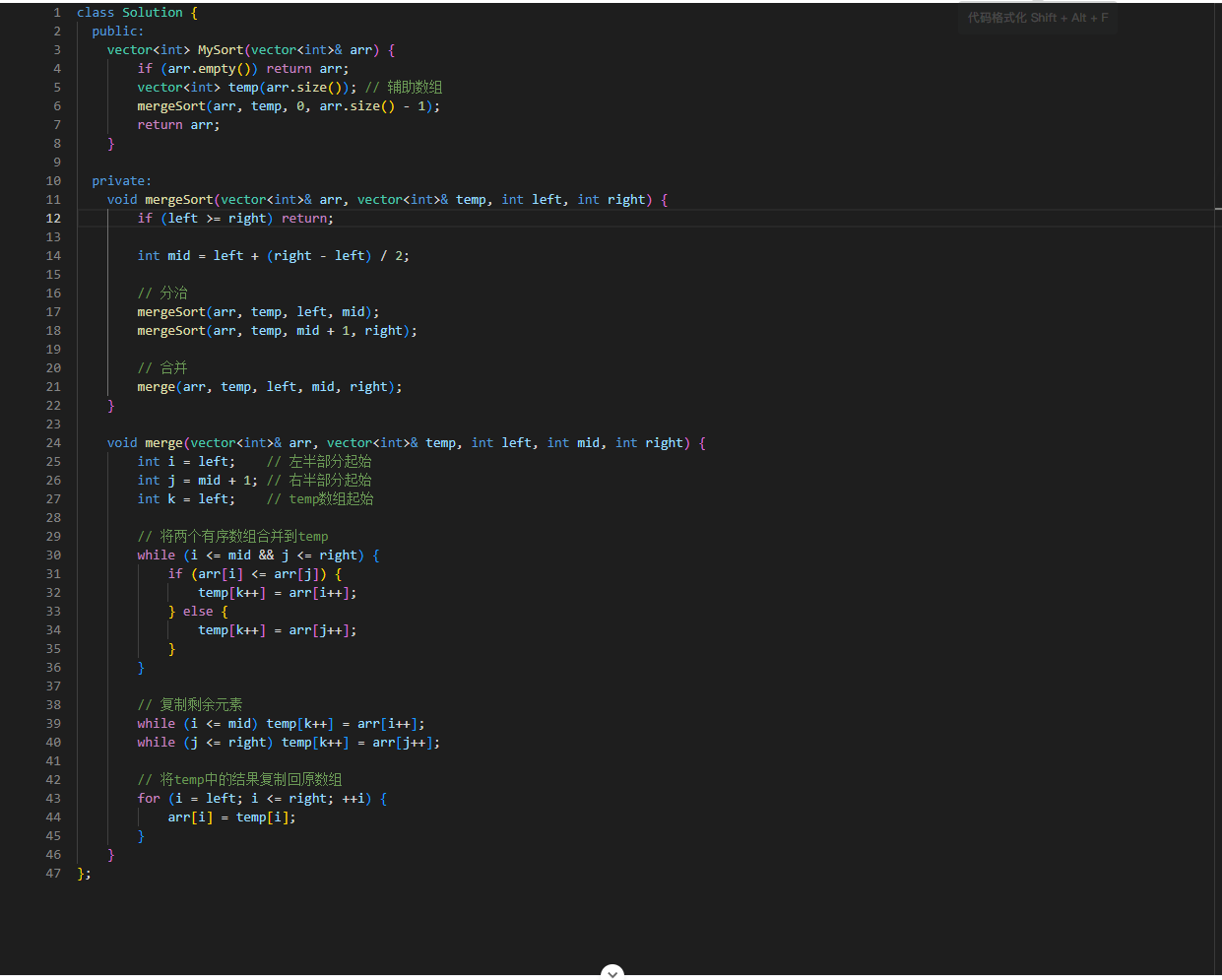
这段代码实现了一个归并排序 (Merge Sort) 算法，用于对整数数组进行升序排序。归并排序是一种基于分治思想的高效排序算法，时间复杂度为 O (n log n)。

逐段逻辑解析

1. 主函数 MySort

vector<int> MySort(vector<int>& arr) {
    if (arr.empty()) return arr;  // 边界条件：空数组直接返回
    vector<int> temp(arr.size()); // 创建辅助数组，避免频繁创建销毁
    mergeSort(arr, temp, 0, arr.size() - 1); // 调用递归排序函数
    return arr;
}

• 作用：作为排序的入口函数，处理边界情况并初始化必要资源。
• 关键点：提前创建一个与原数组大小相同的辅助数组 temp，避免在递归过程中反复创建和销毁数组，优化性能。

2. 递归分治函数 mergeSort

void mergeSort(vector<int>& arr, vector<int>& temp, int left, int right) {
    if (left >= right) return; // 递归终止条件：子数组长度为1时已排序

    int mid = left + (right - left) / 2; // 计算中点，避免溢出

    // 分：递归排序左半部分和右半部分
    mergeSort(arr, temp, left, mid);
    mergeSort(arr, temp, mid + 1, right);

    // 治：合并两个已排序的子数组
    merge(arr, temp, left, mid, right);
}

• 作用：实现 “分治” 中的分步骤。
• 递归终止条件：当子数组的左右边界重合（left >= right）时，说明子数组只有一个元素，天然有序，直接返回。
• 分治策略：将数组从中间一分为二，分别递归排序左半部分和右半部分，然后调用 merge 函数将它们合并。
• 中点计算：mid = left + (right - left) / 2 比 (left + right) / 2 更安全，可以避免整数溢出。

3. 合并函数 merge

void merge(vector<int>& arr, vector<int>& temp, int left, int mid, int right) {
    int i = left;    // 左半部分起始指针
    int j = mid + 1; // 右半部分起始指针
    int k = left;    // temp数组的写入指针

    // 比较两个有序子数组的元素，按升序写入temp
    while (i <= mid && j <= right) {
        if (arr[i] <= arr[j]) {
            temp[k++] = arr[i++];
        } else {
            temp[k++] = arr[j++];
        }
    }

    // 复制左半部分剩余元素
    while (i <= mid) temp[k++] = arr[i++];
    // 复制右半部分剩余元素
    while (j <= right) temp[k++] = arr[j++];

    // 将temp中排好序的部分复制回原数组arr
    for (i = left; i <= right; ++i) {
        arr[i] = temp[i];
    }
}

• 作用：实现 “分治” 中的治步骤，将两个已排序的子数组合并成一个有序数组。
• 合并过程：
  1. 用两个指针 i 和 j 分别指向左右两个子数组的起始位置。
  2. 比较指针指向的元素，将较小的元素放入辅助数组 temp，并移动对应指针。
  3. 当其中一个子数组遍历完后，将另一个子数组的剩余元素直接追加到 temp。
  4. 最后将 temp 中合并好的有序数据复制回原数组 arr 的对应位置。

输入与输出分析

• 输入：一个整数类型的 vector<int>& 引用，可以是无序的整数数组。
• 输出：返回排序后的同一个 vector<int>（原地排序，但也返回了结果）。

使用与扩展指南

• 使用方法：创建 Solution 类的实例，调用 MySort 方法并传入待排序的数组即可。
• 扩展性：
  • 可以轻松修改为降序排序，只需将 merge 函数中的比较条件 arr[i] <= arr[j] 改为 arr[i] >= arr[j]。
  • 可以通过模板编程使其支持更多数据类型（如 float, double）。

总结

1. 核心思想：归并排序采用分治策略，先递归地将数组拆分为最小单元，再自底向上合并有序子数组。
2. 关键步骤：mergeSort 负责拆分，merge 负责合并，辅助数组 temp 用于暂存合并结果。
3. 算法特性：稳定排序（相等元素的相对位置不变），时间复杂度稳定为 O (n log n)，空间复杂度为 O (n)（需要辅助数组）。

---

题目链接

快乐数

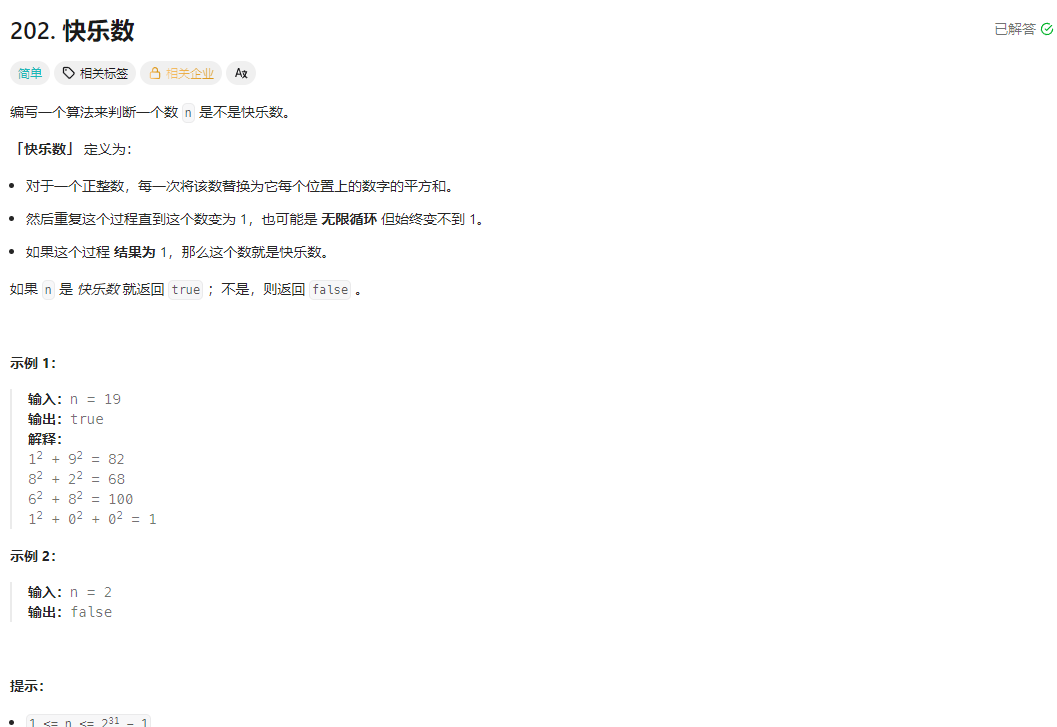
题目描述

题目解析

总体功能概述

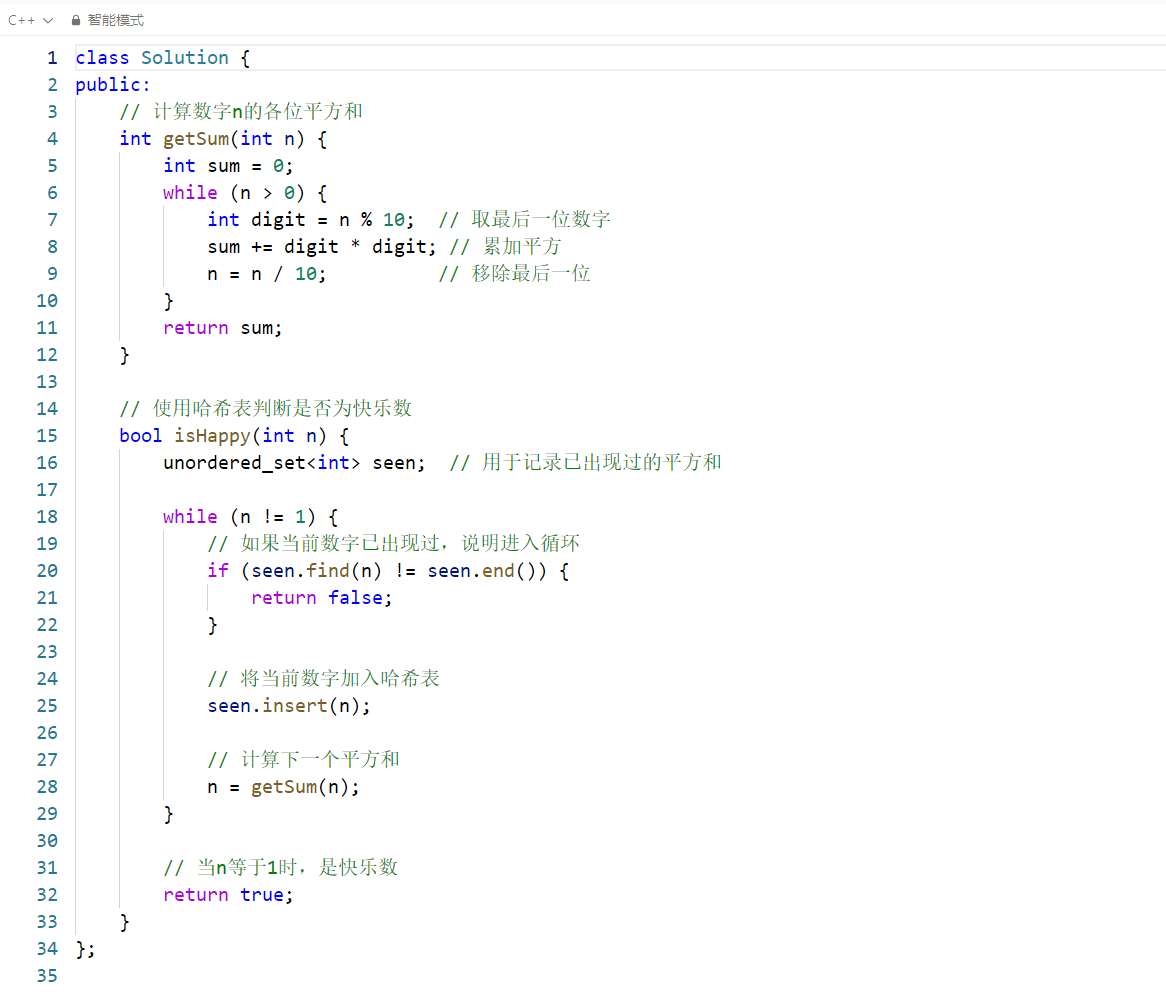
这段代码实现了判断一个整数是否为快乐数 (Happy Number) 的功能。快乐数的定义是：从任意正整数开始，将其各位数字的平方和替换原数，重复此过程，最终如果结果收敛到 1，则为快乐数；如果进入不包含 1 的循环，则不是快乐数。

逐段逻辑解析

1. 辅助函数 getSum

int getSum(int n) {
    int sum = 0;
    while (n > 0) {
        int digit = n % 10;  // 取最后一位数字
        sum += digit * digit; // 累加平方
        n = n / 10;          // 移除最后一位
    }
    return sum;
}

• 作用：计算一个整数 n 的各位数字的平方和。
• 实现逻辑：
  • 使用 n % 10 提取当前数字的最后一位。
  • 将该位数字的平方累加到 sum 中。
  • 使用 n = n / 10 去掉最后一位数字，继续处理剩余部分。
  • 当 n 变为 0 时，返回累加的平方和。

2. 主函数 isHappy

bool isHappy(int n) {
    unordered_set<int> seen;  // 用于记录已出现过的平方和
    
    while (n != 1) {
        // 如果当前数字已出现过，说明进入循环
        if (seen.find(n) != seen.end()) {
            return false;
        }
        
        // 将当前数字加入哈希表
        seen.insert(n);
        
        // 计算下一个平方和
        n = getSum(n);
    }
    
    // 当n等于1时，是快乐数
    return true;
}

• 核心思想：使用哈希集合（unordered_set）来检测循环。如果一个数字重复出现，说明计算过程进入了无限循环，永远无法得到 1。
• 执行流程：
  1. 初始化一个空集合 seen，用于存储已经出现过的数字。
  2. 进入循环，直到 n 变为 1：
     • 检查当前 n 是否在 seen 中：如果在，说明进入循环，返回 false。
     • 如果不在，将 n 加入集合，避免后续重复检测。
     • 调用 getSum(n) 计算下一个平方和，更新 n。
  3. 当 n 等于 1 时，跳出循环，返回 true。

输入与输出分析

• 输入：一个正整数 n。
• 输出：布尔值 true（是快乐数）或 false（不是快乐数）。

示例：

• 输入 19：
  • 1² + 9² = 82
  • 8² + 2² = 68
  • 6² + 8² = 100
  • 1² + 0² + 0² = 1 → 返回 true
• 输入 2：
  • 2² = 4 → 4² = 16 → 1² + 6² = 37 → ... → 最终进入循环，返回 false

使用与扩展指南

• 使用方法：创建 Solution 类的实例，调用 isHappy 方法并传入待判断的整数即可。
• 算法优化：这段代码使用哈希集合的空间复杂度为 O (log n)，也可以用快慢指针法（Floyd 判圈算法）将空间复杂度优化到 O (1)，通过两个指针一快一慢遍历，若相遇则说明存在循环。

总结

1. 快乐数判断逻辑：核心是通过计算各位平方和迭代，直到结果为 1（快乐数）或出现重复数字（进入循环，非快乐数）。
2. 循环检测手段：使用哈希集合记录已出现的数字，是检测循环的直观方法；也可通过快慢指针法优化空间。
3. 关键函数分工：getSum 负责计算平方和，isHappy 负责逻辑控制和循环检测，职责清晰。