目录
2)Acwing --- 242 - 一个简单的整数问题(区间修改+单点查询)
3)Acwing --- 243 - 一个简单的整数问题2(区间修改+区间查询)
1) Acwing --- 243 - 一个简单的整数问题2(区间修改+区间查询)
引入知识:
lowbit操作,原理:

代码实现:
int lowbit(int x){
return x&-x;
}一、树状数组
1. 可以解决的操作
1) 快速求前缀和 -O(logn)
2) 修改某一个数 -O(logn)
一般情况下,是否用树状数组做某个题,就是看是不是只有这两种操作,否则做不了。
注意:树状数组只能解决区间求和问题,解决不了最值问题。
2. 基本原理
可以参考: 树状数组 - OI Wiki
基于二进制实现:
假设 x=2 ^ i [k] + 2 ^ i [k - 1] + 2 ^ i [k - 2] + ... + 2 ^ i [1] , i [k] >= i [k - 1] >= i [k - 2] >= ... >=i[1]
我们可以将 x 划分为以下 k 个区间:
( 1 ) : [ x - 2 ^ i [1] , x ] 包含2 ^ i [1]个数
( 2 ) : [ x - 2 ^ i [2] - 2 ^ i [1] , x - 2 ^ i [1] ] 包含2 ^ i [2]个数
........
( k ) : [ x , x - 2 ^ i [k - 1] - 2 ^ i [k - 2] - ... - 2 ^ i [1] ] 包含2 ^ i [k]个数
观察右端点,我们可以发现区间( L,R ]长度一定是R的二进制最后一位表示的最后一位1所对应的次幂,所以区间可以表示为 [ R-lowbit(R)+1 , R ] ;
令C[x] =a [ x-lowbit(x)+1 , x ]
接下来,观察C[ x ]( 表示区间[ x-lowbit(x)+1 , x ]中所有数的和 ),不难看出1~x所有数的和最多可以划分为log(x)个区间,因此算总和可以用log(x)的时间复杂度。
假设原数组a:1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9 , 10 , 11 , 12 , 13 , 14 , 15 , 16
则c[ 1 ]=1 , c[ 3 ]=3 , c[ 5 ]=5 , c[ 7 ]=7 , c[ 9 ]=9 , c[ 11 ]=11 , c[ 13 ]=13 , c[ 15 ]=15 ,
c[ 2 ]=sum{ 1 , 2} , c[ 4 ]=sum{ 1 , 2 , 3 , 4 } , c[ 6 ]=sum{ 5 , 6 },
c[ 8 ]=sum{ 1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 } , c[ 10 ]=sum{ 9 , 10 },c[ 12 ]=sum{9 , 10 , 11 , 12}
c[ 14 ]=sum{ 13 , 14 }
c[ 16 ]=sum{ 1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9 , 10 , 11 , 12 , 13 , 14 , 15 , 16 }
如下图所示:

初始化:for(int i=1;i<=n;i++)add(i,a[i]); //O(logn)
假设x=......10000 ,则C[ x ]=以x结尾,长度为2^4的区间和,求[ x-2^4+1,x ] 区间和,则 第一段区间:( ......01110 , ......01111 ] ,
第二段区间:( ......01100 , ......01110 ] ,
第三段区间:( ......01000 , ......01100 ] ,
第四段区间:( ......00000 , ......01000 ] ,
即 C[ x ]=a[ x ]+C[ 15 ]+C[ 14 ]+C[ 12 ]+C[ 8 ]。
C [ i ]:表示已 i 结尾的长度为lowbit(i)的区间和。
修改操作:修改的过程是每次在二进制的最后的1加上1。
假设修改a[ 7 ] , 则C[ 7 ]、C[ 8 ]、C[ 16 ]都会改变。
因此,假设a[ x ]+= y , 则for(int i=x;i <= n;i += lowbit(i)) C[ i ] += y ;
查询操作(求1~x的和):查询的过程是每次去掉二进制的最后1位1(lowbit 操作)。
for(int i=x; i ;i -= lowbit(i)) C[ i ] += y;
3. 基本应用
--- 区间修改+单点查询
--- 区间修改+区间查询
--- 二维区间修改+区间查询
--- 偏序问题(逆序对+离散化)
---区间最值
1)Acwing --- 241 - 楼兰图腾
题目来源:https://www.acwing.com/problem/content/243/
问题描述:

代码如下:
#include<bits/stdc++.h>
using namespace std;
typedef unsigned long long ull;
typedef long long ll;
const int N=2e5+10;
int n;
int a[N],tr[N];//a表示原数组,tr表示树状数组
int Greater[N],lower[N];//Greater[k]:1~k-1中比a[k]大的数的个数,lower[k]1~k-1中比a[k]小的数的个数
int lowbit(int x){
return x&-x;
}
void add(int x,int c){//修改
for(int i=x;i<=n;i+=lowbit(i))tr[i]+=c;
}
int sum(int x){//查询前缀和
int res=0;
for(int i=x;i>0;i-=lowbit(i))res+=tr[i];
return res;
}
void solve(){
scanf("%d",&n);
for(int i=1;i<=n;i++)scanf("%d",&a[i]);
for(int i=1;i<=n;i++){
int y=a[i];
Greater[i]=sum(n)-sum(y);//1~y-1中有多少个大于y的数
lower[i]=sum(y-1);//1~y-1中有多少个小于y的数
add(y,1);//把这个数加进树状数组中,表示数字y出现次数多1
}
memset(tr,0,sizeof tr);
ll res1=0,res2=0;
for(int i=n;i>0;i--){
int y=a[i];
res1+=Greater[i]*(ll)(sum(n)-sum(y));//左边比y大的数*y+1~n中比y大的数
res2+=lower[i]*(ll)sum(y-1);//
add(y,1);//把这个数加进树状数组中,表示数字y出现次数多1
}
cout<<res1<<" "<<res2<<endl;
}
int main(){
int t;
t=1;
//cin>>t;
while(t--){
solve();
}
return 0;
}2)Acwing --- 242 - 一个简单的整数问题(区间修改+单点查询)
原题链接:https://www.acwing.com/problem/content/248/
题目描述:

代码如下:
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=1e5+10;
int n,m;
int a[N];
ll tr[N];
int lowbit(int x){
return x&-x;
}
void add(int x,int c){
for(int i=x;i<=n;i+=lowbit(i))tr[i]+=c;
}
ll sum(int x){
ll res=0;
for(int i=x;i;i-=lowbit(i))res+=tr[i];
return res;
}
void solve(){
cin>>n>>m;
for(int i=1;i<=n;i++)cin>>a[i],add(i,a[i]-a[i-1]);
while(m--){
char op[2];
int l,r,d;
cin>>op>>l;
if(op[0]=='C'){
cin>>r>>d;
add(l,d),add(r+1,-d); //差分
}else{
cout<<sum(l)<<endl;
}
}
}
int main(){
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
int t;
t=1;
//cin>>t;
while(t--){
solve();
}
return 0;
}3)Acwing --- 243 - 一个简单的整数问题2(区间修改+区间查询)
原题链接:https://acwing.com/problem/content/244/
问题描述:

思路:
1. 原数组a变成差分数组b---求a[l~r]+c ---> b[ l ] += c ; b[ r + 1 ] -= c ;
2. 求S=a[1]+...+a[x]
for(int i=1;i<=x;i++)
for(int j=1;j<=i;j++)
S += b[j];

代码如下:
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=1e5+10;
ll n,m;
ll a[N];
ll tr1[N],tr2[N];//tr[1]:维护差分数组b[i]的前缀和,tr2[i]维护b[i]*i的前缀和
ll lowbit(ll x){
return x&-x;
}
void add(ll tr[],ll x,ll c){
for(int i=x;i<=n;i+=lowbit(i))tr[i]+=c;
}
ll sum(ll tr[],ll x){
ll res=0;
for(int i=x;i;i-=lowbit(i))res+=tr[i];
return res;
}
ll prefix_sum(ll x){
return sum(tr1,x)*(x+1)-sum(tr2,x);
}
int main(){
cin>>n>>m;
for(int i=1;i<=n;i++)cin>>a[i];
for(int i=1;i<=n;i++){
ll b=a[i]-a[i-1];
add(tr1,i,b);
add(tr2,i,(ll)b*i);
}
while(m--){
char op[2];
ll l,r,d;
cin>>op>>l>>r;
if(op[0]=='Q'){
cout<<prefix_sum(r)-prefix_sum(l-1)<<endl;
}else{
cin>>d;;
add(tr1,l,d),add(tr2,l,l*d);
add(tr1,r+1,-d),add(tr2,r+1,-(r+1)*d);
}
}
}4)Acwing --- 244 - 谜一样的牛
原题链接:https://www.acwing.com/problem/content/245/
题目描述:

思路:
假设有n头牛,第 i 头牛前面有a[ i ]头牛比第 i 头牛矮的牛,则第 i 头牛应该是剩下的牛中排行第a[ i ]+1的牛
1.从剩余的数中,找出第 k 小的数 <--->找到最小的一个x,使得sum(x)=k(sum(x)表示1~x中剩余多少个数) 2. 删除某个数
首先,a[1]~a[n]=1,表示每个身高可以用一次,然后用树状数组维护a[1]~a[n]的前缀和。
代码如下:
#include<bits/stdc++.h>
using namespace std;
const int N=1e5+10;
int n;
int h[N],ans[N],tr[N];
int lowbit(int x){
return x&-x;
}
void add(int x,int c){
for(int i=x;i<=n;i+=lowbit(i))tr[i]+=c;
}
int sum(int x){
int res=0;
for(int i=x;i;i-=lowbit(i))res+=tr[i];
return res;
}
int main(){
cin>>n;
h[1]=0;
for(int i=2;i<=n;i++)cin>>h[i];
for(int i=1;i<=n;i++)tr[i]=lowbit(i);
for(int i=n;i;i--){
int k=h[i]+1;
int l=1,r=n;
while(l<r){
int mid=l+r>>1;
if(sum(mid)>=k)r=mid;
else l=mid+1;
}
ans[i]=r;
add(r,-1);
}
for(int i=1;i<=n;i++)cout<<ans[i]<<endl;
}二、线段树(一)
1.最简单的线段树的四种基本操作
1)push up(u):由子节点算父节点的信息
2)build ():将一段区间初始化成线段树
3)modify():修改某个点或者区间---1. 修改单点 2. 修改区间 push down(又称懒标记或延迟标记):把当前父节点的修改信息更新到子节点
4)query()
2.原理

除最后一层外,是满二叉树 ---> 用一维数组存储
编号是x的点:父节点编号是 x/2(x>>1) 下取整,左儿子编号是 2x(x<<1),右儿子编号是 2x+1(x<<1|1)。
整棵树有n个叶子结点,除了最后一层一共2n-1个点,最坏情况下,最后一层是倒数第二层的两倍,因此最坏情况下,整棵树有4n-1个结点。
build(int u,int l,int r){
tr[n].l=l,tr[n.r=r;
if(l==r)return ;
int mid=l+r>>1;
build(u<<1,l,mid),build(u<<1|1,mid+1,r);
}
3. 应用
1)Acwing --- 1275 - 最大数
问题描述:
给定一个正整数数列 a1,a2,…,an,每一个数都在 0∼p−1 之间。
可以对这列数进行两种操作:
1. 添加操作:向序列后添加一个数,序列长度变成 n+1;
2. 询问操作:询问这个序列中最后 L 个数中最大的数是多少。
程序运行的最开始,整数序列为空。
写一个程序,读入操作的序列,并输出询问操作的答案。
输入格式
第一行有两个正整数 m,p,意义如题目描述;
接下来 m 行,每一行表示一个操作。
如果该行的内容是 Q L,则表示这个操作是询问序列中最后 L 个数的最大数是多少;
如果是 A t,则表示向序列后面加一个数,加入的数是 (t+a) mod p。其中,t 是输入的参数,a 是在这个添加操作之前最后一个询问操作的答案(如果之前没有询问操作,则 a=0)。
第一个操作一定是添加操作。对于询问操作,L>0 且不超过当前序列的长度。
输出格式
对于每一个询问操作,输出一行。该行只有一个数,即序列中最后 L 个数的最大数。
数据范围
1≤m≤2×105,
1≤p≤2×109,
0≤t<p
输入样例
10 100
A 97
Q 1
Q 1
A 17
Q 2
A 63
Q 1
Q 1
Q 3
A 99
输出样例
97
97
97
60
60
97
思路:
1. 在某个位置修改一个数
2. 在某一个区间内的最大值

struct Node{
int l,r; //左右端点
int v; //记录区间内的最大值 //一般存某个区间的某种属性(看这个属性能不能由两个子区间的属性算出来,不能的话,再存一些其他属性)
}
代码如下:
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=2e5+5;
int m,p;
struct Node{
int l,r;
int v;//区间l~r的最大值
}tr[N*4];
void pushup(int u){//由子节点的信息,来计算父节点的信息
tr[u].v=max(tr[u<<1].v,tr[u<<1|1].v);
}
void build(int u,int l,int r){
tr[u]={l,r};
if(l==r)return ;
int mid=(l+r)>>1;
build(u<<1,l,mid),build(u<<1|1,mid+1,r);
}
int query(int u,int l,int r){
if(tr[u].l>=l&&tr[u].r<=r)return tr[u].v;//树中节点已经被完全包含在[l,r]中了
int mid=tr[u].l+tr[u].r>>1;
int v=0;
if(l<=mid)v=query(u<<1,l,r);
if(r>mid)v=max(v,query(u<<1|1,l,r));
return v;
}
void modify(int u,int x,int v){
if(tr[u].l==x&&tr[u].r==x)tr[u].v=v;
else{
int mid=tr[u].l+tr[u].r>>1;
if(x<=mid)modify(u<<1,x,v);
else modify(u<<1|1,x,v);
pushup(u);
}
}
void solve(){
int n=0,a=0;//n表示当前数据的个数
cin>>m>>p;
build(1,1,m);
char op[2];
int x;
while(m--){
cin>>op>>x;
if(op[0]=='Q'){
a=query(1,n-x+1,n);
cout<<a<<endl;
}else{
modify(1,n+1,(a+x)%p);
n++;
}
}
}
int main(){
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
int t;
t=1;
//cin>>t;
while(t--){
solve();
}
return 0;
}2)Acwing --- 245 - 你能回答这些问题吗
原题链接:https://www.acwing.com/problem/content/246/
问题描述:

思路:
1. 单点修改
2. 查询区间内的最大字段和
struct Node{
int l,r; //区间左右端点
int tmax; //最大连续字段和
int lmax; //最大前缀和
int rmax; //最大后缀和
int sum; //区间和
}
tmax=max(左儿子的tamx,右儿子的tmax,左儿子的rmax+右儿子的lmax);


代码如下:
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=5e5+10;
int n,m;
int w[N];
struct Node{
int l,r;
int sum,lmax,rmax,tmax;
}tr[N*4];
void pushup(Node &u,Node &l,Node &r){//u是l和r的父节点
u.sum=l.sum+r.sum;
u.lmax=max(l.lmax,l.sum+r.lmax);
u.rmax=max(r.rmax,r.sum+l.rmax);
u.tmax=max(max(l.tmax,r.tmax),l.rmax+r.lmax);
}
void pushup(int u){
pushup(tr[u],tr[u<<1],tr[u<<1|1]);
}
void build(int u,int l,int r){
if(l==r)tr[u]={l,r,w[r],w[r],w[r],w[r]};
else{
tr[u]={l,r};
int mid=l+r>>1;
build(u<<1,l,mid),build(u<<1|1,mid+1,r);
pushup(u);
}
}
int modify(int u,int x,int v){
if(tr[u].l==x&&tr[u].r==x)tr[u]={x,x,v,v,v,v};
else{
int mid=tr[u].l+tr[u].r>>1;
if(x<=mid)modify(u<<1,x,v);
else modify(u<<1|1,x,v);
pushup(u);
}
}
Node query(int u,int l,int r){
if(tr[u].l>=l&&tr[u].r<=r)return tr[u];
else{
int mid=tr[u].l+tr[u].r>>1;
if(r<=mid)return query(u<<1,l,r);
else if(l>mid)return query(u<<1|1,l,r);
else{
auto left=query(u<<1,l,r);
auto right=query(u<<1|1,l,r);
Node res;
pushup(res,left,right);
return res;
}
}
}
void solve(){
cin>>n>>m;
for(int i=1;i<=n;i++)cin>>w[i];
build(1,1,n);
int k,x,y;
while(m--){
cin>>k>>x>>y;
if(k==1){
if(x>y)swap(x,y);
cout<<query(1,x,y).tmax<<endl;
}else modify(1,x,y);
}
}
int main(){
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
int t;
t=1;
//cin>>t;
while(t--){
solve();
}
return 0;
}3)Acwing --- 246 - 区间最大公约数
原题链接:https://www.acwing.com/problem/content/247/
问题描述:

代码如下:
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=5e5+10;
int n,m;
ll w[N];
struct Node{
int l,r;
ll sum,d;
}tr[N*4];
ll gcd(ll a,ll b){
return b?gcd(b,a%b):a;
}
void pushup(Node &u,Node &l,Node &r){
u.sum=l.sum+r.sum;
u.d=gcd(l.d,r.d);
}
void pushup(int u){
pushup(tr[u],tr[u<<1],tr[u<<1|1]);
}
void build(int u,int l,int r){
if(l==r){
ll b=w[r]-w[r-1];
tr[u]={l,r,b,b};
}else{
tr[u]={l,r};
int mid=l+r>>1;
build(u<<1,l,mid),build(u<<1|1,mid+1,r);
pushup(u);
}
}
void modify(int u,int x,ll v){
if(tr[u].l==x&&tr[u].r==x){
ll b=tr[u].sum+v;
tr[u]={x,x,b,b};
}else{
int mid=tr[u].l+tr[u].r>>1;
if(x<=mid)modify(u<<1,x,v);
else modify(u<<1|1,x,v);
pushup(u);
}
}
Node query(int u,int l,int r){
//if(l>r)return {0};
if(tr[u].l>=l&&tr[u].r<=r)return tr[u];
else{
int mid=tr[u].l+tr[u].r>>1;
if(r<=mid)return query(u<<1,l,r);
else if(l>mid)return query(u<<1|1,l,r);
else{
auto left=query(u<<1,l,r),right=query(u<<1|1,l,r);
Node res;
pushup(res,left,right);
return res;
}
}
}
void solve(){
cin>>n>>m;
for(int i=1;i<=n;i++)cin>>w[i];
build(1,1,n);
int l,r;
char op[2];
ll d;
while(m--){
cin>>op>>l>>r;
if(op[0]=='Q'){
auto left=query(1,1,l);
Node right={0,0,0,0};
if(l+1<=r)right=query(1,l+1,r);
cout<<abs(gcd(left.sum,right.d))<<endl;
}else{
cin>>d;
modify(1,l,d);
if(r+1<=n)modify(1,r+1,-d);
}
}
}
int main(){
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
int t;
t=1;
//cin>>t;
while(t--){
solve();
}
return 0;
}三、线段树(二)
懒标记
add表示:给以当前结点为根的子树中的每一个结点加上add(不包含根结点)
pushdown操作:
left.add+=root.add;left.sum+(left.r-left.l)*root.add;
right.add+=root.add;right.sum+(right.r-right.l)*root.add;
root.add=0;
1) Acwing --- 243 - 一个简单的整数问题2(区间修改+区间查询)
原题链接:https://acwing.com/problem/content/244/
问题描述:

代码如下:
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=1e5+10;
int n,m;
int w[N];
struct Node{
int l,r;
ll sum,add;
}tr[N*4];
void pushup(int u){
tr[u].sum=tr[u<<1].sum+tr[u<<1|1].sum;
}
void pushdown(int u){
auto &root=tr[u],&left=tr[u<<1],&right=tr[u<<1|1];
if(root.add){
left.add+=root.add,left.sum+=(ll)(left.r-left.l+1)*root.add;
right.add+=root.add,right.sum+=(ll)(right.r-right.l+1)*root.add;
root.add=0;
}
}
void build(int u,int l,int r){
if(l==r)tr[u]={l,r,w[r],0};
else{
tr[u]={l,r};
int mid=l+r>>1;
build(u<<1,l,mid),build(u<<1|1,mid+1,r);
pushup(u);
}
}
void modify(int u,int l,int r,int d){
if(tr[u].l>=l&&tr[u].r<=r){
tr[u].sum+=(ll)(tr[u].r-tr[u].l+1)*d;
tr[u].add+=d;
}else{
pushdown(u);
int mid=tr[u].l+tr[u].r>>1;
if(l<=mid)modify(u<<1,l,r,d);
if(r>mid)modify(u<<1|1,l,r,d);
pushup(u);
}
}
ll query(int u,int l,int r){
if(tr[u].l>=l&&tr[u].r<=r)return tr[u].sum;
pushdown(u);
int mid=tr[u].l+tr[u].r>>1;
ll sum=0;
if(l<=mid)sum+=query(u<<1,l,r);
if(r>mid)sum+=query(u<<1|1,l,r);
pushup(u);
return sum;
}
void solve(){
cin>>n>>m;
for(int i=1;i<=n;i++)cin>>w[i];
build(1,1,n);
char op[2];
int l,r,d;
while(m--){
cin>>op>>l>>r;
if(op[0]=='C'){
cin>>d;
modify(1,l,r,d);
}else{
cout<<query(1,l,r)<<endl;
}
}
}
int main(){
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
int t=1;
//cin>>t;
while(t--)solve();
return 0;
}2)Acwing --- 247 - 亚特兰蒂斯
问题描述:

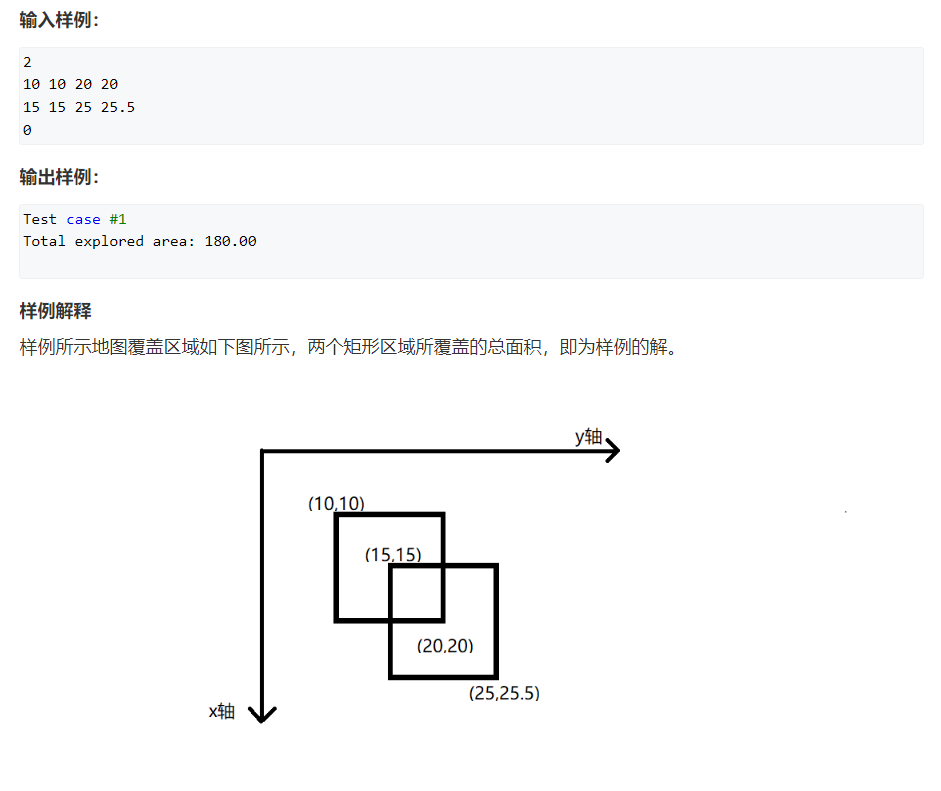
思路:
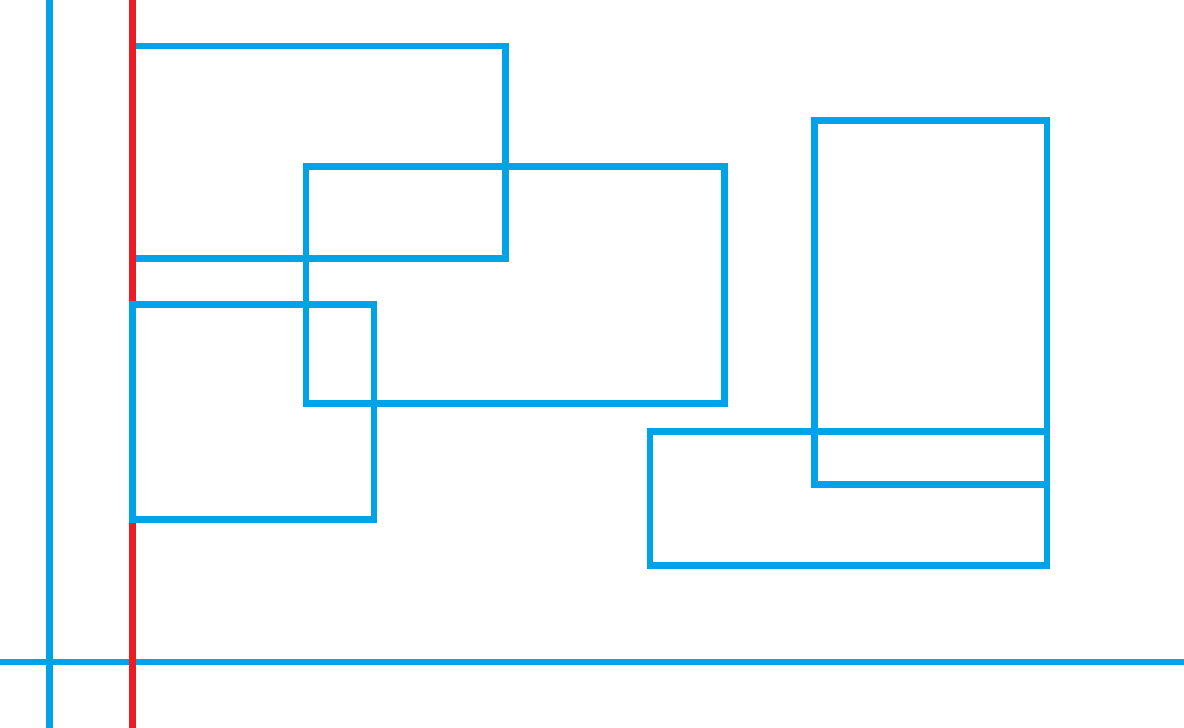
将垂直x轴的边画一条直线,如下图:
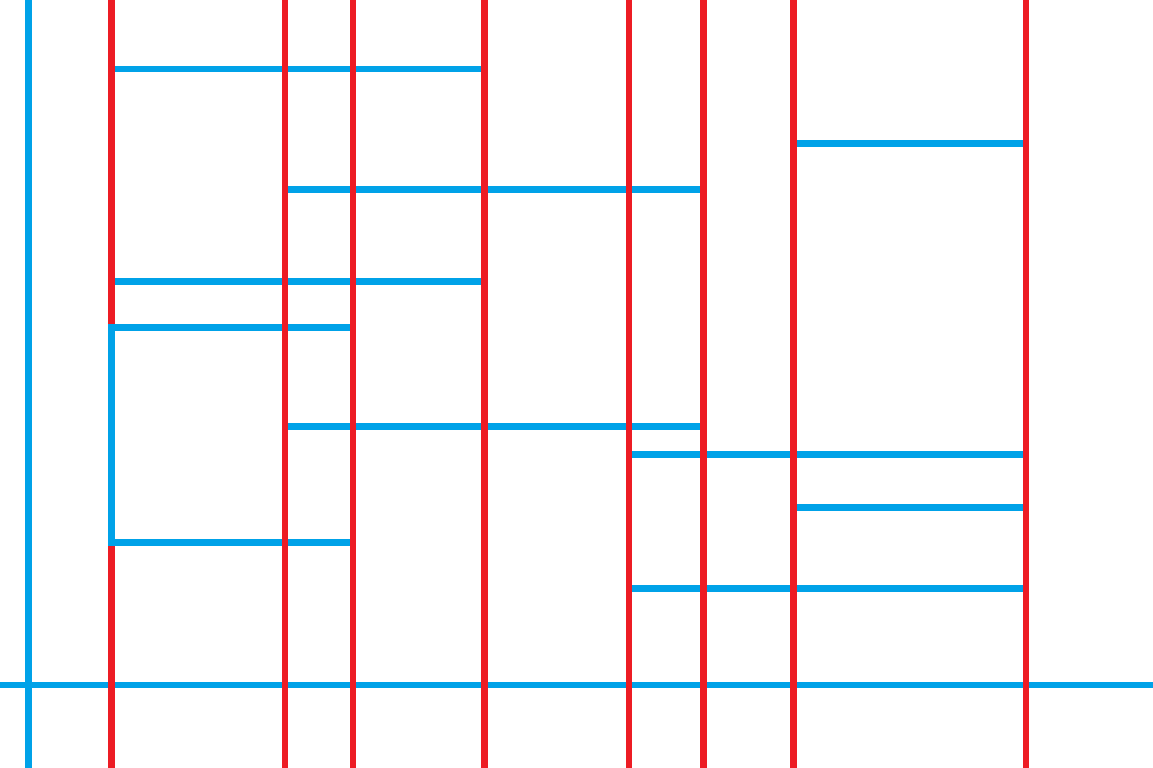
面积为:
S=h[1]*(x[2]-x[1]) + h[2]*(x[3]-x[2]) + ... +h[i]*(x[i+1]-x[i])
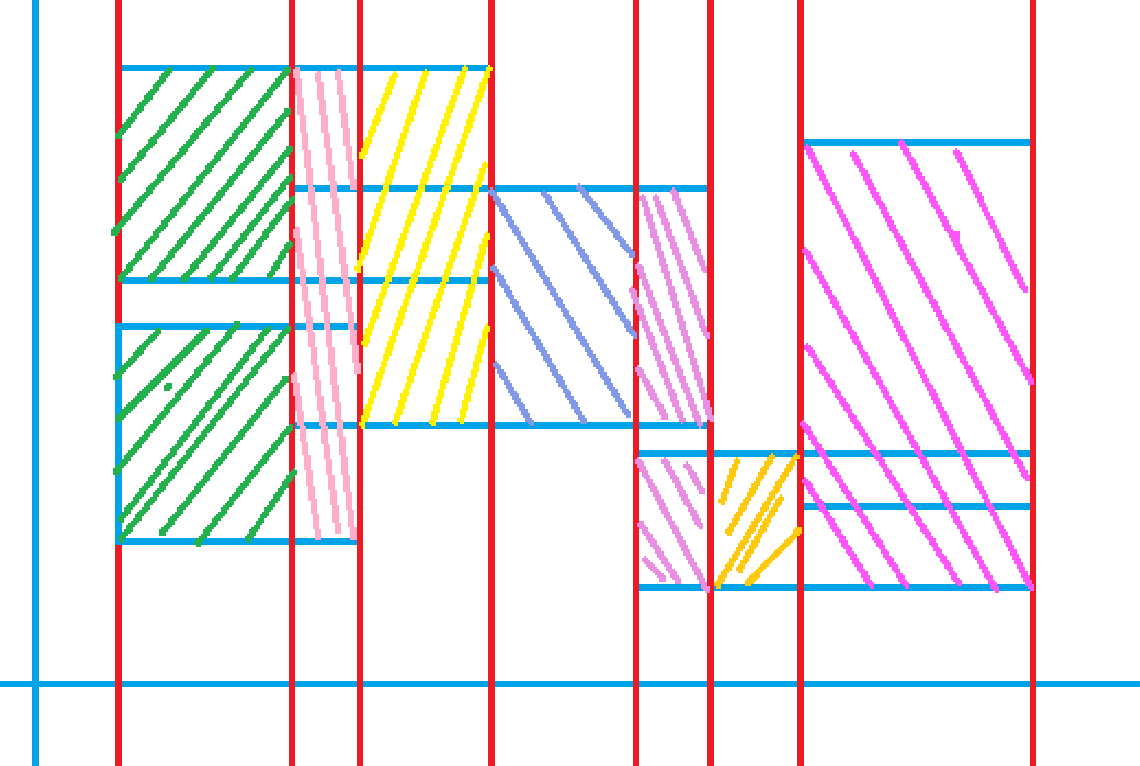
将每个矩形的左右两条边做成带权值的边,如图:
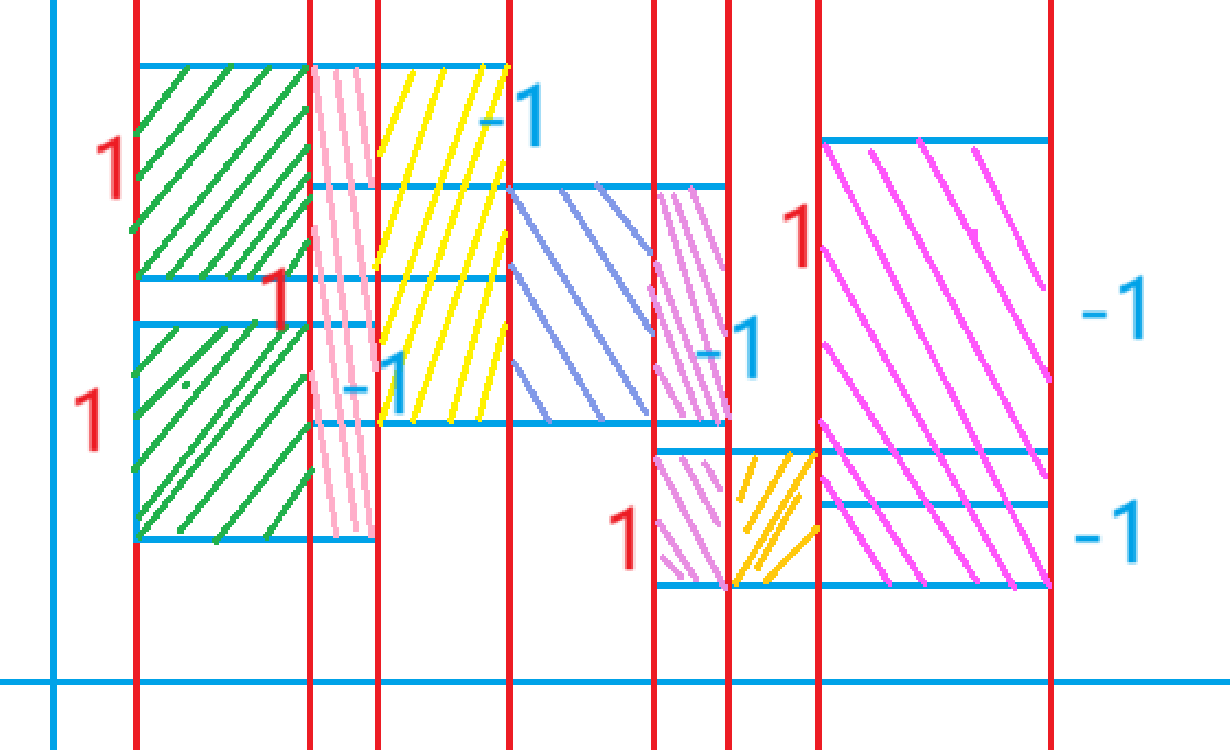
将y轴做成线段树,将每个带权值的线段所对应y轴的区间+对应边的权值
操作一:将某个区间[ l , r ] + k 操作二:整个区间中长度大于0的区间总长是多少
cnt:表示当前区间整个被覆盖的次数
len:不考虑祖先结点cnt的前提下(永远只往下看),cnt>0的区间总长
扫描线性质:
1. 永远只考虑根节点信息 ---说明query时,不会用到pushdown
2. 所有的操作均是成对出现且先加后减 ---modify时,也不会用到pushdown
代码如下:
#include <iostream>
#include <cstring>
#include <algorithm>
#include <vector>
using namespace std;
const int N = 100010;
struct segment// 用来存线段信息
{
double x, y1,y2;
int d; // 区分它是该矩阵前面的线段还是后面的线段
bool operator < (const segment&t)const
{
return x < t.x;
}
}seg[N * 2];//每个矩阵需要存两个线段
struct node
{
int l,r;
int cnt;// 记录这段区间出现了几次
double len;// 记录这段区间的长度;即线段长度
}tr[N * 8];//由于线段二倍,所以8倍空间
vector<double>ys;//用于离散化
int n;
int find(double y)
{
// 需要返回vector 中第一个 >= y 的数的下标
return lower_bound(ys.begin(), ys.end(), y) - ys.begin();
}
void pushup(int u)
{
if(tr[u].cnt)tr[u].len = ys[tr[u].r + 1] - ys[tr[u].l];//表示整个区间都被覆盖,该段长度就为右端点 + 1后在ys中的值 - 左端点在ys中的值
else if(tr[u].l != tr[u].r)tr[u].len = tr[u << 1].len + tr[u << 1 | 1].len;
else tr[u].len = 0;//表示为叶子节点且该线段没被覆盖,为无用线段,长度变为0
}
void modify(int u,int l,int r,int d)//表示从线段树中l点到r点的出现次数 + d
{
if(tr[u].l >= l && tr[u].r <= r)//该区间被完全覆盖
{
tr[u].cnt += d;//该区间出现次数 + d
pushup(u);//更新该节点的len
}
else
{
int mid = tr[u].r + tr[u].l >> 1;
if (l <= mid)modify(u << 1,l,r,d);//左边存在点
if (r > mid)modify(u << 1 | 1,l,r,d);//右边存在点
pushup(u);//进行更新
}
}
void build(int u,int l,int r)
{
tr[u] = {l,r,0,0};
if (l != r)
{
int mid = l + r >> 1;
build(u << 1,l,mid),build(u << 1 | 1,mid + 1,r);
//后面都为0,不需更新len
}
}
int main()
{
int T = 1;
while (cin>>n,n)
{
ys.clear();
int j = 0;//一共j个线段
for (int i = 0 ; i < n ; i ++)//处理输入
{
double x1,y1,x2,y2;
cin>>x1>>y1>>x2>>y2;
seg[j ++] = {x1,y1,y2,1};//前面的线段
seg[j ++] = {x2,y1,y2,-1};//后面的线段
ys.push_back(y1),ys.push_back(y2);//y轴出现过那些点
}
sort(seg,seg + j);//线段按x排序
sort(ys.begin(),ys.end());//先排序
ys.erase(unique(ys.begin(),ys.end()),ys.end());//离散化去重
build(1,0,ys.size() - 2);
double res = 0;
for (int i = 0 ; i < j ; i ++)
{
//根节点的长度即为此时有效线段长度 ,再 * x轴长度即为面积
if (i)res += tr[1].len * (seg[i].x - seg[i - 1].x);
//处理一下该线段的信息,是加上该线段还是消去
modify(1,find(seg[i].y1), find(seg[i].y2) - 1,seg[i].d);
}
printf("Test case #%d\n", T ++ );
printf("Total explored area: %.2lf\n\n", res);
}
return 0;
} 2)Acwing --- 1277 - 维护序列

代码如下:
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 1e5 + 5;
int t;
int m, n, p;
int w[N];
struct node
{
int l, r;
ll sum, add, mul;
}tr[N*4];
void pushup(int u)
{
tr[u].sum = (tr[u << 1].sum + tr[u << 1 | 1].sum) % p;
}
void change(node &now,ll add,ll mul)
{
now.sum = (now.sum*mul + (ll)(now.r - now.l + 1)*add) % p;
now.mul = now.mul*mul%p;
now.add = (now.add*mul + add) % p;
}
void pushdown(int u)//向下更新
{
change(tr[u << 1], tr[u].add, tr[u].mul);
change(tr[u << 1 | 1], tr[u].add, tr[u].mul);
tr[u].add = 0, tr[u].mul = 1;//往下传后,当前层清空懒标记
}
void build(int u, int l, int r)
{
if (l == r)tr[u] = { l,l,w[l],0,1 };
else
{
tr[u] = { l,r,0,0,1 };
int mid = l + r >> 1;
build(u << 1, l, mid), build(u << 1 | 1, mid + 1, r);
pushup(u);
}
}
void modify(int u, int l, int r, int add, int mul)
{
if (tr[u].l >= l && tr[u].r <= r)change(tr[u], add, mul);
//树中结点,打上懒标记,查询时会更新
else//继续往下走
{
pushdown(u);
int mid = tr[u].l + tr[u].r >> 1;
if (l <= mid)modify(u << 1, l, r, add, mul);
if (r > mid)modify(u << 1 | 1, l, r, add, mul);
pushup(u);
}
}
ll query(int u, int l, int r)
{
if (tr[u].l >= l && tr[u].r <= r)return tr[u].sum;
pushdown(u);//往下走时通过懒标记,更新子节点
int mid = tr[u].l + tr[u].r >> 1;
ll sum = 0;
if (l <= mid)sum = sum+query(u << 1, l, r)%p;
if (r > mid)sum += query(u << 1 | 1, l, r);
return sum%p;
}
int main()
{
scanf("%d%d", &n, &p);
f(int i=1, i<=n, i++)scanf("%d", &w[i]);
build(1, 1, n);
scanf("%d", &m);
int a, b,c,d;
while (m--)
{
scanf("%d%d%d", &a, &b, &c);
if (a == 1)
{
scanf("%d", &d);
modify(1, b, c, 0, d);
}
else if (a == 2)
{
scanf("%d", &d);
modify(1, b, c, d, 1);
}
else printf("%lld\n", query(1, b, c));
}
return 0;
}



















 2922
2922

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








