线段树 & 树状数组

理解了线段树和树状数组我觉得，这两有必要记录一下。在写力扣第307题的时候我看了一眼，这还算中等难度啊？可能是最优解算中等难度吧，暴力法我觉得效率都挺高的啊，先写出来再思考一下最优解吧。两分钟写完提交，超时？？？更新时间复杂度为O(1)，求和时间复杂度为O(n)这都能超时？？？

我开始怀疑人生，思考了一下，应该是需要记录求和的状态减少求和次数，想到了前缀和，但是前缀和在更新了一个数之后也需要O(n)来更新前缀和，不妥。想了想应该是需要分区间计算总和，但分几个区间呢，如果跨区间还得特殊处理好麻烦，而且效率也高不到哪去，算了看看答案吧。好吧，第一个方法还真是分区间。姑且看一看吧：

一、分块处理

首先解决了我提的问题，分多少区间合适？答案是开根号，块数和块内元素都是一样的，同为n^(1/2)（打不出根号，跟我念：根号n）记作size，举例n=8，size=sqrt(n)=2

既然分出了块数size，那么需要记录每个块数之和，记作vector<int> sum

分析一下三个函数：

（1）构造函数：需要额外创建sum并遍历填值，时间复杂度和空间复杂度额外添加了O(根号n)，但整体复杂度仍为O(n)

（2）更新函数：只需要将对应的sum中去掉原值再加上新值就好了(加上差值)，更改num对应值，时间复杂度仍为O(1)

（3）区间求和：左右边缘区间需要一个个增加，中间直接用sum解决复杂度由O(n)降为O(根号n)，详细看下文：

需要特殊处理跨区间问题，存在几种情况：

（1）同一区间内：sum没用了，老老实实一个个加吧，同一区间内证明数最多也就size个，复杂度也就是O(根号n)

比如：[1,2,3][4,5,6][7,8,9]，我找4到6的和，直接4,5,6相加即可

（2）跨相邻区间：左区间的右边占一点，右区间的左边占一点，操作同上，需要两次相加而已，sum无用

比如：[1,2,3][4,5,6][7,8,9]，我找2到5的和，2,3相加，4,5相加，再相加即可

（3）跨多区间：sum终于派上用场了，边缘两区间仍需要进行逐个相加，中间的直接使用sum就好了

比如：[1,2,3][4,5,6][7,8,9][10,11,12][13,14,15]，我找2到14的和，2,3相加，13,14相加，中间再加上三个sum

上官方解答：

class NumArray {
private:
    vector<int> sum; // sum[i] 表示第 i 个块的元素和
    int size; // 块的大小
    vector<int> &nums;
public:
    NumArray(vector<int>& nums) : nums(nums) {
        int n = nums.size();
        size = sqrt(n);
        sum.resize((n + size - 1) / size); // n/size 向上取整
        for (int i = 0; i < n; i++) {
            sum[i / size] += nums[i];
        }
    }

    void update(int index, int val) {
        sum[index / size] += val - nums[index];
        nums[index] = val;
    }

    int sumRange(int left, int right) {
        int b1 = left / size, i1 = left % size, b2 = right / size, i2 = right % size;
        if (b1 == b2) { // 区间 [left, right] 在同一块中
            return accumulate(nums.begin() + b1 * size + i1, nums.begin() + b1 * size + i2 + 1, 0);
        }
        //左边缘区间
        int sum1 = accumulate(nums.begin() + b1 * size + i1, nums.begin() + b1 * size + size, 0);
        //右边缘区间
        int sum2 = accumulate(nums.begin() + b2 * size, nums.begin() + b2 * size + i2 + 1, 0);
        //中间区间直接用sum优化计算
        int sum3 = accumulate(sum.begin() + b1 + 1, sum.begin() + b2, 0);
        return sum1 + sum2 + sum3;
    }
};

构造函数时间复杂度为O(n)，更新操作为O(1)，求和操作为O(根号n)（原为O(n)）

空间复杂度从O(1)到O(根号n)

二、线段树

线段树理解起来倒不是很难，写起来也不难只是比较繁琐。上图（百度百科的图）：

线段树每一个节点的值等于左节点和右节点之和，每一个输入元素都在叶节点上。查找的时间复杂度为O(logN)。而未优化的空间复杂度为2N，实际应用时一般还要开4N的数组以免越界，因此有时需要离散化让空间压缩。当然，我们这里就不进行离散化了。

同样分析三个函数：

（1）构造函数：需要额外创建segmentTree的数组（堆型存储）并自下而上遍历填值（后序遍历），毕竟要求和，肯定得从下往上建树，时间复杂度和空间复杂度额外添加了O(n)，但整体复杂度仍为O(n)

（2）更新函数：需要更改叶子节点的对应值，并将所有的祖先节点全部更改，同样是自下而上，时间复杂度仍为O(logn)

（3）区间求和：每个节点的值为子节点的和，那么，刚好为此区间我直接获取该节点的值即可，不再则向下遍历。时间复杂度为O(logn)。同样涉及到跨边界问题，但是不难，举个例子即可：

如上图，若我要获取1到5的和，直接获取[1,5]的节点值即可，

若是1到4的和，则获取[1,3]+[4,4]即可。

上官方代码：

class NumArray {
private:
    vector<int> segmentTree;
    int n;

    void build(int node, int s, int e, vector<int> &nums) {
        if (s == e) {
            segmentTree[node] = nums[s];
            return;
        }
        int m = s + (e - s) / 2;
        build(node * 2 + 1, s, m, nums);
        build(node * 2 + 2, m + 1, e, nums);
        segmentTree[node] = segmentTree[node * 2 + 1] + segmentTree[node * 2 + 2];
    }

    void change(int index, int val, int node, int s, int e) {
        if (s == e) {
            segmentTree[node] = val;
            return;
        }
        int m = s + (e - s) / 2;
        if (index <= m) {
            change(index, val, node * 2 + 1, s, m);
        } else {
            change(index, val, node * 2 + 2, m + 1, e);
        }
        segmentTree[node] = segmentTree[node * 2 + 1] + segmentTree[node * 2 + 2];
    }

    int range(int left, int right, int node, int s, int e) {
        if (left == s && right == e) {
            return segmentTree[node];
        }
        int m = s + (e - s) / 2;
        if (right <= m) {
            return range(left, right, node * 2 + 1, s, m);
        } else if (left > m) {
            return range(left, right, node * 2 + 2, m + 1, e);
        } else {
            return range(left, m, node * 2 + 1, s, m) + range(m + 1, right, node * 2 + 2, m + 1, e);
        }
    }

public:
    NumArray(vector<int>& nums) : n(nums.size()), segmentTree(nums.size() * 4) {
        build(0, 0, n - 1, nums);
    }

    void update(int index, int val) {
        change(index, val, 0, 0, n - 1);
    }

    int sumRange(int left, int right) {
        return range(left, right, 0, 0, n - 1);
    }
};

构造时间复杂度为O(n)，区间求和时间复杂度为O(logn),更新时间复杂度为O(logn)

关于为什么要4N的节点数，我们举个最好情况和最坏情况的例子即可：

最好情况（2N-1）（完全二叉树）：

 这个时候叶子节点为N=8，总结点数，也就是总占有空间为2N-1=15。

同样的如果新增节点在最左边也满足完全二叉树，同样也是2N-1。

最坏情况（新增节点在最底层右边，左边都为空）：

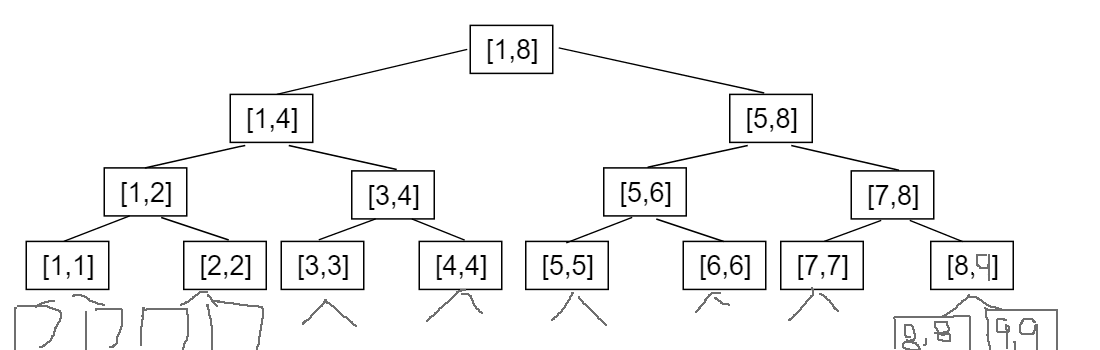
 最底层的右边有新增节点，而最底层其它节点全部为空，也就是实际元素为N=9，但需要31个节点空间，即4N是确保最坏情况下都能保证不越界的范围。

三、树状数组

树状数组第一次接触的时候我以为是堆型数组的别称，但其实差别挺大。

树状数组或二叉索引树（英语：Binary Indexed Tree），又以其发明者命名为Fenwick树，其初衷是解决数据压缩里的累积频率（Cumulative Frequency）的计算问题，现多用于高效计算数列的前缀和， 区间和。

原本的二叉树是像上图那种，而树形数组的二叉树如下图所示：

有点抽象，我们举个例子看看，用了树状数组（尽量详细了）_浪漫毁灭者的博客-优快云博客_树状数组的图：

输入数组记为C[N]，节点数组记为A[N]

举个例子：输入的常规数组C[N]={0,1,2,3,4,5,6,7,8}                //方便理解，第一个节点不用

则树状数组为A[N]={0,1,3,3,10,5,11,7,36}                                //方便理解，第一个节点不用

解释：

A[1] = C[1] = 1;

A[2] = A[1] + C[2] = 1 + 2 = 3;

A[3] = C[3] = 3;

A[4] = A[2] + A[3] + C[4] = 3 + 3 + 4 = 10;

A[4]节点记录了A[2]和A[3]节点的值加上本身C[4]的值，而A[2]又包含了A[1]节点，也就是A[4]节点包含了C[1]，C[2]，C[3]节点的值再加上C[4]本身的值。

知道了何为树状数组，我们来看看是如何实现的

（1）更新函数：假设要改动C[3],在所有包含A[3]的节点中加上差值（新值-旧值）即可，包括了A[4],A[8],A[16]，重复直至全部完成,时间复杂度为O(logn)。如何判断哪些节点包含呢，这就涉及到lowBit()函数了，见下文

（2）构造函数：创建A[N]初始化为0，然后对每个C[i]都进行一次更新函数即可完成，时间复杂度为O(nlogn)

（3）区间求和：这个问题可以先转换为求右边界的前缀和，然后再减去左边界的前缀和，则为区间和。

（4）前缀和：初始和为0，加上上一个找到比自己节点数多的节点值，直至全部包含。举例，我要求15的前缀和，找到14（包含了2个节点），找到12（包含了4个节点），找到8（包含8个），前缀和则为sum = A[15] + A[14] + A[12] + A[8]。那么问题来了，如何找到上一个节点呢，也是通过lowBit()函数。

（5）lowBit()：树状数组的精华函数，lowBit(int x){return x&(-x)}，我们可以换个图来考虑，将十进制转换为二进制来考虑：

 更新过程需要找到包含该节点的节点，也就是5(101) -> 6(110) -> 8(1000)，通过x += x & (-x)实现

x & (-x)这块可得好好讲一讲，我们都知道负数以补码的形式表示，以-5举例应该010+001=011

5 & (-5) = (101) & (011) = 001，也就是说下一个包含的节点应该是5+1=6

同样再看看6，6 & (-6) = (110) & (010) = 010，下一个节点应该是6+2=8

8同理，8&-8=1000,下一个节点应该是8+8=16

这样x += lowBit(x)的意思是包含自己的下一个节点，那么x -= lowBit(x)呢？

x=5的话，上一个节点为4，再上一个为0

x=6，上一个同样为4

x=15呢？lowBit(15) = 1 ，lowBit(14) = 2，lowBit(12) = 4 ，lowBit(8) = 8，也就是图中的蓝色路径

x -= lowBit(x)就是找到自己的上一个最高位，1010上一个最高位就是去掉0010变成1000

x+= lowBit(x)就是找到自己的下一个最高位，1010下一个最高位就是1100

位运算真是个好东西

上官方代码：

class NumArray {
private:
    vector<int> tree;            //A[N]
    vector<int> &nums;           //C[N]

    int lowBit(int x) {
        return x & -x;
    }

    void add(int index, int val) {
        while (index < tree.size()) {
            tree[index] += val;
            index += lowBit(index);
        }
    }

    int prefixSum(int index) {
        int sum = 0;
        while (index > 0) {
            sum += tree[index];
            index -= lowBit(index);
        }
        return sum;
    }

public:
    NumArray(vector<int>& nums) : tree(nums.size() + 1), nums(nums) {
        for (int i = 0; i < nums.size(); i++) {
            add(i + 1, nums[i]);
            // for (int i = 0; i < nums.size()+1; i++) {
            //     cout<<tree[i]<<" ";
            // }cout<<endl;
            //这里是观看建树的步骤，方便理解
        }
    }

    void update(int index, int val) {
        add(index + 1, val - nums[index]);
        nums[index] = val;
    }

    int sumRange(int left, int right) {
        return prefixSum(right + 1) - prefixSum(left);
    }
};