【数据结构进阶】手撕红黑树

🔥个人主页： Forcible Bug Maker
🔥专栏： C++ || 数据结构

🌈前言

本篇博客主要内容：红黑树的介绍，以及底层代码逻辑和实现。

刚刚接触编程的时候就听说有的大厂HR会让手撕红黑树。心中一直对这个数据结构保持着敬畏和向往，今天在将其撕出来后，用本篇博客加以记录，望周知。

🔥红黑树的概念

红黑树，也是一种二叉搜索树，但再每个结点上增加一个存储位置表示结点的颜色，可以是RED（红）或BLACK（黑）。通过对任何一条根到叶子的路径上各个结点的着色方式的限制，红黑树确保没有一条路径会比其他路径长出两倍，因而是接近平衡的。

一颗红黑树，是具有如下性质的二叉搜索树：

1. 每个结点不是红色就是黑色
2. 根结点是黑色的
3. 如果一个结点是红色，则它的两个孩子结点是黑色（即不会有连续的红结点）
4. 对于每个结点，从该结点到其所有后代叶结点的简单路径上，均包含相同数目的黑色结点
5. 每个叶子结点都是黑色的（此处的叶子结点指的是空结点NIL）

其中，3和4是最重要的两点。

🔥手撕红黑树

红黑树结点的定义

红黑树的结点包含四个成员变量，模板类型T：可以存储K或者pair<K,V>类型，便于后期封装；三个指针：分别为指向左孩子结点的指针，指向右孩子结点的指针，指向父结点的指针；最后变量_col：枚举类型，可以存RED和BLACK。

enum Color
{
   
	RED,
	BLACK
};

template<class T>
struct RBTreeNode
{
   
	RBTreeNode<T>(const T& t)
		: _data(t)
		, _left(nullptr)
		, _right(nullptr)
		, _parent(nullptr)
		, _col(RED)
	{
   }
	T _data;
	RBTreeNode<T>* _left;
	RBTreeNode<T>* _right;
	RBTreeNode<T>* _parent;
	Color _col;
};

红黑树主体需要实现的成员函数

// T: 可能是键值对<key,value>
//    可能是一个key
// 不论节点中存储的是<key, value> || key, 都是按照key来进行比较的
// KeyOfValue: 提取data中的Key
template<class K, class T, class KeyOfValue>
class RBTree
{
   
	typedef RBTreeNode<T> Node;
public:
	typedef RBTreeIterator<T, T&, T*> iterator;
	typedef RBTreeIterator<T, const T&, const T*> const_iterator;
public:
	RBTree() = default;

	RBTree(const RBTree<K, T, KeyOfValue>& t);

	// 插入值为data的节点
	// 返回值含义：iterator代表新插入节点   bool：代表释放插入成功
	std::pair<iterator, bool> Insert(const T& data);
	
	// Begin和End迭代器
	iterator Begin();
	iterator End();

	// 红黑树是否为空，是返回true，否则返回false
	bool Empty()const;
	
	// 返回红黑树中有效节点的个数
	size_t Size()const;
	
	// 将红黑树中的有效节点删除
	void Clear();

	// 检测红黑树是否为有效的红黑树，注意：其内部主要依靠_IsValidRBTRee函数检测
	bool IsValidRBTRee()
	
	// 在红黑树中查找data，存在赶回该节点对应的迭代器，否则返回End()
	iterator Find(const T& data);

	~RBTree();
private:
	Node* _root;
};

红黑树的插入

红黑树是在二叉搜索树的基础上加上其平衡限制条件，因此红黑树的插入可分为两步：

1. 首先是按照二叉搜索树的方式插入结点
2. 检测插入结点后，红黑树的性质是否遭到破坏
   因为新结点的默认颜色是红色，因此：如果父结点的颜色是黑色，就没有违反性质，不需调整；担当插入结点的父节点也是红色时，就违反了性质3（不能有连在一起的红结点），此时需要对红黑树分情况讨论调整：

约定：cur为当前结点，p为父节点，g为祖父结点，u为叔叔结点。

• 情况一：cur为红，p为红，g为黑，u存在且为红

解决方式：将p，u变成黑色，g变成红色，然后把g改成cur，继续向上调整。

• 情况二：cur为红，p为红，g为黑，u不存在/u存在且为黑（这里需要做的其实就和AVL树中的单旋很像了，我们需要把u结点旋转下来，以维持平衡）

p为g的左孩子，cur为p的左孩子，进行右单旋；相反，p为g的右孩子，cur为p的右孩子，则进行左单旋。p变黑色，g变红色。

• 情况三（情况二的变体）：cur为红，p为红，g为黑，u不存在/u存在且为黑（其实就是双旋，除了不用调整平衡因子，其他的和AVL树的双旋并无差别）

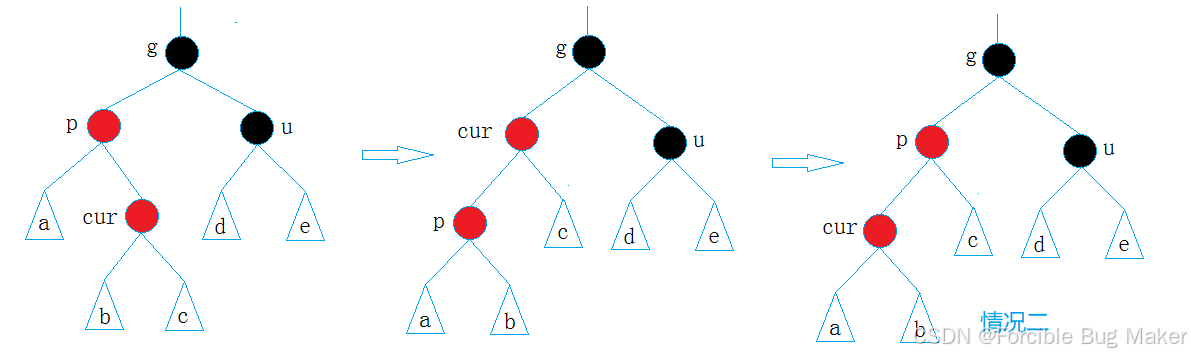
p为g的左孩子，cur为p的右孩子，则针对p做左单旋转；相反，p为g的右孩子，cur为p的左孩子，则针对p做右单旋转。然后就转换成了情况2。

针对每种情况进行相应的处理即可：

// 插入值为data的节点
// 返回值含义：iterator代表新插入节点   bool：代表释放插入成功
std::pair<iterator, bool> Insert(const T& data)
{
   
	if (_root == nullptr) {
   
		_root = new Node(data);
		_root->_col = BLACK;
		return std::make_pair(iterator(_root, _root), true);
	}

	KeyOfValue kov;

	Node* parent = nullptr;
	Node* cur = _root;
	while (cur) {
   
		if (kov(cur->_data) < kov(data)) {
   
			parent = cur;
			cur = cur