【C++进阶】带你手撕红黑树（红与黑的爱恨厮杀）

🪐🪐🪐欢迎来到程序员餐厅💫💫💫

          主厨：邪王真眼

主厨的主页：Chef‘s blog  

 所属专栏：c++大冒险
 

 总有光环在陨落，总有新星在闪烁

---

引言：

        之前我们学习了 AVL树，不得不惊叹于他那近乎绝对的平衡，然而也惋惜于插入删除效率的低下，今天要讲的红黑树则是以相对的平衡换来了插入删除效率的大幅提高，可谓是各有千秋

ps：建议先看过AVL树后再来学习红黑树：

带你手撕AVL树 

---

一. 红黑树的概念

         红黑树是一种二叉搜索树，但在每个结点上增加一个存储位表示结点的颜色，可以是Red或 Black。 通过对任何一条从根到叶子的路径上各个结点着色方式的限制，红黑树确保没有一条路径会比其他路径长出俩倍，因而是接近平衡的。

二 红黑树的性质

• 1. 每个结点不是红色就是黑色
• 2. 根节点是黑色的 
• 3. 如果一个节点是红色的，则它的两个孩子结点是黑色的 
• 4. 对于每个结点，从该结点到其所有后代叶结点的简单路径上，均包含相同数目的黑色结点 
• 5. 每个叶子结点都是黑色的(此处的叶子结点指的是空结点)

思考：

为什么满足以上性质，红黑树就能保证：最长路径中节点个数不会超过最短路径节点 个数的2倍？

推导：

• 性质1不必多说
• 性质2与后面的旋转有关
• 性质3表明不能有连续的红色结点
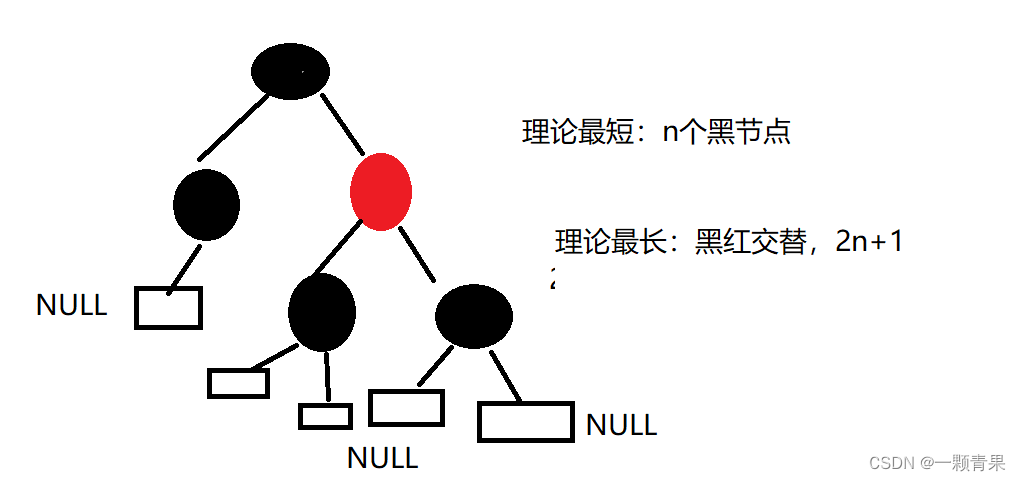
• 性质4表明理论最短路径就是纯黑节点路径

综上：

            我们可以认为事先建造好一颗纯黑节点的满二叉树，再在两个黑节点之间插入红节点，则理论最长路径就是一黑一红交替，不超过最短路径的二倍。

 三.红黑树的节点讲解及模拟

enum Color
{
	RED,
	BLACK
};
template<class K, class V>
struct RBTreeNode
{
	RBTreeNode<K, V>* _left;
	RBTreeNode<K, V>* _right;
	RBTreeNode<K, V>* _parent;
	pair<K, V> _kv;
	Color _col;
	RBTreeNode(pair<K, V>& kv = pair<K, V>())
		:_left(nullptr)
		, _right(nullptr)
		, _parent(nul