蒙特卡洛方法与 MCMC 采样

一、蒙特卡洛方法

1. 蒙特卡洛方法Monte Carlo 可以通过采用随机投点法来求解不规则图形的面积。

   求解结果并不是一个精确值，而是一个近似值。当投点的数量越来越大时，该近似值也越接近真实值。

2. 蒙特卡洛方法也可以用于根据概率分布来随机采样的任务。

1.1 布丰投针问题

1. 布丰投针问题是1777年法国科学家布丰提出的一种计算圆周率的方法：随机投针法。其步骤为：

   • 首先取一张白纸，在上面绘制许多条间距为  的平行线。

   • 取一根长度为  的针，随机地向纸上投掷  次，观测针与直线相交的次数，记做  。

   • 计算针与直线相交的概率  。可以证明这个概率  。因此有：

2. 由于向纸上投针是完全随机的，因此用二维随机变量  来确定针在纸上的具体位置。其中：

   • 表示针的中点到平行线的距离，它是 之间的均匀分布。
   • 表示针与平行线的夹角，它是 之间的均匀分布。

   

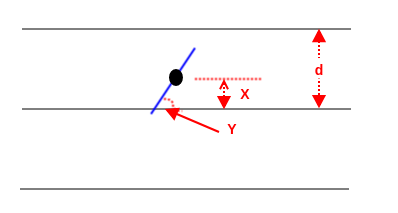
   当  时，针与直线相交。

   由于  相互独立，因此有概率密度函数：

   因此，针与直线相交的概率为：

   根据  即可得证。

3. 布丰投针问题中，蒙特卡洛方法是利用随机投点法来求解面积  。因为曲线的积分就是面积，这里的曲线就是概率密度函数  。

1.2 蒙特卡洛积分

1. 对于函数 ，其在区间  上的积分  可以采用两种方法来求解：投点法、期望法。

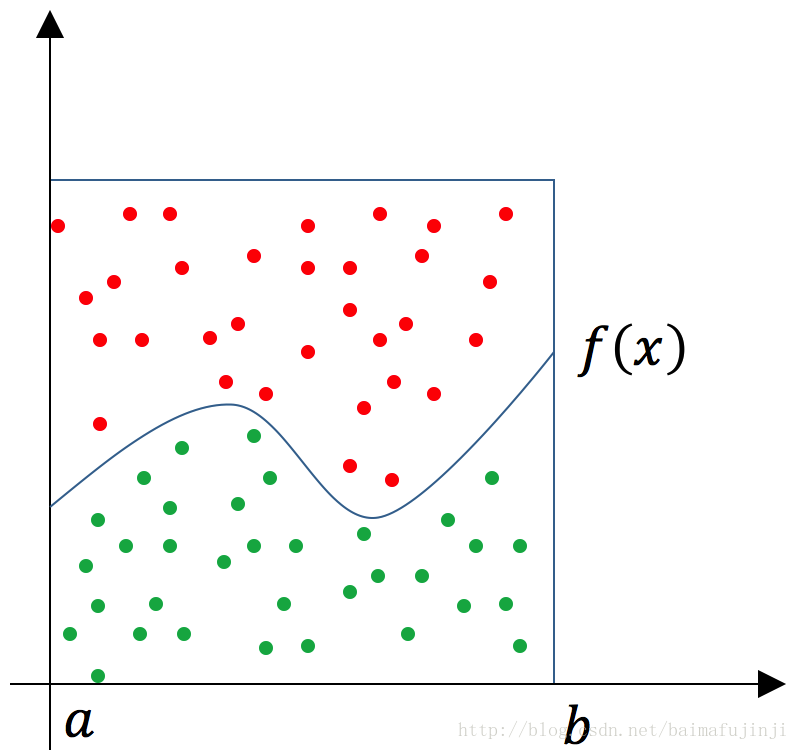
2. 投点法求积分：对函数 ，对其求积分等价于求它的曲线下方的面积。

   此时定义一个常数 ，使得  ，该常数在区间  上的面积就是矩形面积  。

   随机向矩形框中随机的、均匀的投点，设落在函数  下方的点为绿色，落在  和  之间的点为红色。则有：落在  下方的点的概率等于  的面积比上矩形框的面积 。

   具体做法是：从  之间的均匀分布中采样  ，从  之见的均匀分布中采样  ，  构成一个随机点。

   • 若 ，则说明该随机点在函数 下方，染成绿色。
   • 若 ，则说明该随机点在函数 上方，染成红色。

   假设绿色点有  个，红色点有  个，总的点数为  ，因此有： 。

   

3. 期望法求积分：假设需要求解积分  ，则任意选择一个概率密度函数 ，其中  满足条件：

   令：

   则有： ，它刚好是一个期望：设随机变量  服从分布 ，则  。

   则期望法求积分的步骤是：

   • 任选一个满足条件的概率分布 。
   • 根据 ，生成一组服从分布 的随机数 。
   • 计算均值 ，并将 作为 的近似。

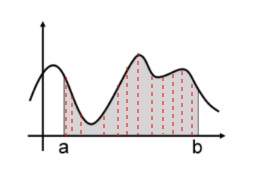
4. 在期望法求积分中，如果  均为有限值，则  可以取均匀分布的概率密度函数：

   此时 ，  。

   其物理意义为： 为在区间  上函数的平均高度，乘以区间宽度  就是平均面积。

   

5. 对于期望 ，如果  或者  的表达式比较复杂，则也可以转化为另一个期望的计算。

   选择一个比较简单的概率密度函数 ，根据：

   令 ，则原始期望转换为求另一个期望  。此时可以使用期望法求积分的策略计算。

1.3 蒙特卡洛采样

1. 采样问题的主要任务是：根据概率分布  ，生成一组服从分布  的随机数  。

   • 如果  就是均匀分布，则均匀分布的采样非常简单。

   • 如果  是非均匀分布，则可以通过均匀分布的采样来实现。其步骤是：

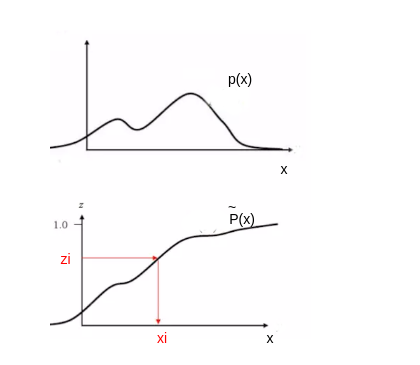
     • 首先根据均匀分布  随机生成一个样本  。

     • 设  为概率分布  的累计分布函数： 。

       令  ，计算得到  ，其中  为反函数，则  为对  的采样。

     

2. 通过均匀分布的采样的原理：假设随机变量  满足 ，则  的概率分布为：

   因为  是  上面的均匀分布，因此  ；  为概率分布  的累计分布函数，因此  。因此上式刚好等于  ，即： 服从概率分布  。

   这其中有两个关键计算：

   • 根据 ，计算累计分布函数 。
   • 根据 计算反函数 。

   如果累计分布函数无法计算，或者反函数难以求解，则该方法无法进行。

3. 对于复杂的概率分布  ，难以通过均匀分布来实现采样。此时可以使用接受-拒绝采样 策略。

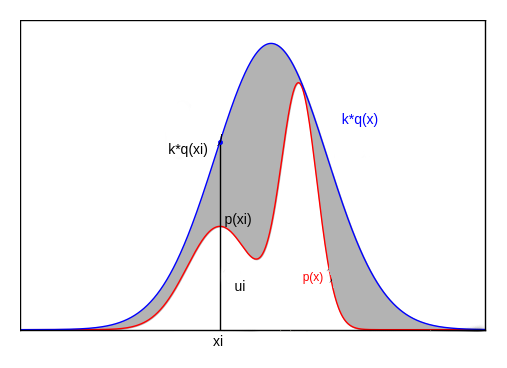
   • 首先选定一个容易采样的概率分布  ，选择一个常数  ，使得在定义域的所有位置都满足  。

   • 然后根据概率分布  随机生成一个样本  。

   • 计算  ，以概率  接受该样本。

     具体做法是：根据均匀分布  随机生成一个点  。如果  ，则接受该样本；否则拒绝该样本。

     或者换一个做法：根据均匀分布  生成一个随机点，如果该点落在灰色区间（）则拒绝该样本；如果该点落在白色区间（）则接受该样本。

   

4. 接受-拒绝采样 在高维的情况下会出现两个问题：

   • 合适的 分布比较难以找到。
   • 难以确定一个合理的 值。

   这两个问题会导致拒绝率很高，无效计算太多。

二、马尔可夫链

1. 马尔可夫链是满足马尔可夫性质的随机过程。

   马尔可夫链  描述了一个状态序列，其中每个状态值取决于前一个状态。 为随机变量，称为时刻  的状态，其取值范围称作状态空间。

   马尔可夫链的数学定义为：  。

2.1 马尔可夫链示例

1. 社会学家把人按照经济状况分成三类：下层、中层、上层。用状态 1,2,3 代表着三个阶层。社会学家发现：决定一个人的收入阶层的最重要因素就是其父母的收入阶层。

   • 如果一个人的收入属于下层，则他的孩子属于下层的概率是 0.65，属于中层的概率是 0.28，属于上层的概率是 0.07 。
   • 如果一个人的收入属于中层，则他的孩子属于下层的概率是 0.15，属于中层的概率是 0.67，属于上层的概率是 0.18 。
   • 如果一个人的收入属于上层，则他的孩子属于下层的概率是 0.12，属于中层的概率是 0.36，属于上层的概率是 0.52 。

   从父代到子代，收入阶层的变化的转移概率如下：

   	子代阶层1	子代阶层2	子代阶层3
   父代阶层1	0.65	0.28	0.07
   父代阶层2	0.15	0.67	0.18
   父代阶层3	0.12	0.36	0.52

2. 使用矩阵的表示方式，转移概率矩阵记作：

   假设当前这一代人在下层、中层、上层的人的比例是概率分布  ，则：

   • 他们的子女在下层、中层、上层的人的概率分布是
   • 他们的孙子代的分布比例将是
   • ....
   • 第 代子孙在下层、中层、上层的人的比例是

3. 假设初始概率分布为  ，给出前 14 代人的分布状况：

     0 0.72 0.19 0.09

     1 0.5073 0.3613 0.1314

     2 0.399708 0.431419 0.168873

     3 0.34478781 0.46176325 0.19344894

     4 0.3165904368 0.4755635827 0.2078459805

     5 0.302059838985 0.482097475693 0.215842685322

     6 0.294554638933 0.485285430346 0.220159930721

     7 0.290672521545 0.486874112293 0.222453366163

     8 0.288662659788 0.487677173087 0.223660167125

     9 0.28762152488 0.488086910874 0.224291564246

     10 0.287082015513 0.488297220381 0.224620764107

     11 0.286802384833 0.488405577077 0.22479203809

     12 0.286657431274 0.488461538107 0.224881030619

     13 0.286582284718 0.488490482311 0.22492723297

     14 0.28654332537 0.488505466739 0.224951207891

   可以看到从第 9 代开始，阶层分布就趋向于稳定不变。

4. 如果换一个初始概率分布为  ，给出前 14 代人的分布状况：

     0 0.51 0.34 0.15

     1 0.4005 0.4246 0.1749

     2 0.345003 0.459586 0.195411

     3 0.31663917 0.47487142 0.20848941

     4 0.3020649027 0.4818790066 0.2160560907

     5 0.294550768629 0.48521729983 0.220231931541

     6 0.290668426368 0.486853301457 0.222478272175

     7 0.288659865019 0.487671049342 0.223669085639

     8 0.28761985994 0.488085236095 0.224294903965

     9 0.287081082851 0.488296834394 0.224622082755

     10 0.286801878943 0.488405532034 0.224792589023

     11 0.286657161801 0.488461564615 0.224881273584

     12 0.286582142693 0.488490512087 0.224927345221

     13 0.28654325099 0.488505487331 0.224951261679

     14 0.286523087645 0.488513240994 0.224963671362

   可以发现到第 8 代又收敛了。

5. 两次不同的初始概率分布，最终都收敛到概率分布  。 这说明收敛的行为和初始概率分布  无关，而是由概率转移矩阵  决定的。

   计算 ：

     0 [[ 0.65  0.28  0.07]

        [ 0.15  0.67  0.18]

        [ 0.12  0.36  0.52]]

     1 [ [ 0.4729  0.3948  0.1323]

         [ 0.2196  0.5557  0.2247]

         [ 0.1944  0.462   0.3436]]

     ...

     18 [[ 0.28650397  0.48852059  0.22497545]

         [ 0.28650052  0.48852191  0.22497757]

         [ 0.28649994  0.48852213  0.22497793]]

     19 [[ 0.28650272  0.48852106  0.22497622]

         [ 0.28650093  0.48852175  0.22497732]

         [ 0.28650063  0.48852187  0.2249775 ]]

     20 [[ 0.28650207  0.48852131  0.22497661]

         [ 0.28650115  0.48852167  0.22497719]

         [ 0.28650099  0.48852173  0.22497728]]

     21 [[ 0.28650174  0.48852144  0.22497682]

         [ 0.28650126  0.48852163  0.22497712]

         [ 0.28650118  0.48852166  0.22497717]]

     ...

   可以看到 ：

   发现当  足够大的时候， 矩阵  收敛且每一行都稳定收敛到  。

2.2 平稳分布

1. 马尔可夫链定理：如果一个非周期马尔可夫链具有转移概率矩阵 ，且它的任何两个状态是联通的，则有：

   其中：

   •  为所有可能的状态。

   •  是转移概率矩阵  的第  行第  列的元素，表示状态  转移到状态  的概率。

   • 概率分布  是方程  的唯一解，其中  。

     称概率分布  为马尔可夫链的平稳分布。

2. 注意，在马尔可夫链定理中：

   • 马尔可夫链的状态不要求有限，可以是无穷多个。

   • 非周期性在实际任务中都是满足的。

   • 两个状态的连通指的是：状态  可以通过有限的  步转移到达  (并不要求从状态  可以直接一步转移到状态  ）。

     马尔可夫链的任何两个状态是联通的含义是：存在一个  ，使得矩阵  中的任何一个元素的数值都大于零。

3. 从初始概率分布  出发，在马尔可夫链上做状态转移，记时刻  的状态  服从的概率分布为 ， 记作  ，则有：

   假设到达第  步时，马尔可夫链收敛，则有：

   所以  都是同分布的随机变量（当然它们并不独立）。

   如果从一个具体的初始状态  开始，然后沿着马尔可夫链按照概率转移矩阵做调整，则得到一个转移序列  。

   根据马尔可夫链的收敛行为，当  较大时，  将是平稳分布  的样本。

4. 定理：如果非周期马尔可夫链的转移矩阵  和某个分布  满足： ，则  是马尔可夫链的平稳分布。

   这被称作马尔可夫链的细致平稳条件detailed balance condition ，其证明如下：

   .

三、MCMC 采样

1. 概率图模型中最常用的采样技术是马尔可夫链蒙特卡罗方法Markov Chain Monte Carlo:MCMC。

   给定连续随机变量  的概率密度函数  ，则  在区间  中的概率可以计算为：

   如果函数 ， 则可以计算  的期望： 。

   • 如果  不是一个单变量，而是一个高维的多元变量  ，且服从一个非常复杂的分布，则对于上式的求积分非常困难。为此，MCMC先构造出服从  分布的独立同分布随机变量  ， 再得到  的无偏估计：

   • 如果概率密度函数  也很复杂，则构造服从  分布的独立同分布随机变量也很困难。MCMC 方法就是通过构造平稳分布为  的马尔可夫链来产生样本。

3.1 MCMC 算法

1. MCMC 算法的基本思想是：先设法构造一条马尔可夫链，使其收敛到平稳分布恰好为  。然后通过这条马尔可夫链来产生符合  分布的样本。最后通过这些样本来进行估计。

   这里马尔可夫链的构造至关重要，不同的构造方法将产生不同的MCMC算法。Metropolis-Hastings:MH算法是MCMC的重要代表。

2. 假设已经提供了一条马尔可夫链，其转移矩阵为  。目标是另一个马尔科夫链，使转移矩阵为  、平稳分布是  。

   通常  ，即  并不满足细致平稳条件不成立。但是可以改造已有的马尔可夫链，使得细致平稳条件成立。

   引入一个函数  ，使其满足： 。如：取  ，则有：

   令：  ，则有  。其中  构成了转移矩阵  。而  恰好满足细致平稳条件，因此它对应的马尔可夫链的平稳分布就是  。

3. 在改造  的过程中引入的  称作接受率。其物理意义为：在原来的马尔可夫链上，从状态  以  的概率跳转到状态  的时候，以  的概率接受这个转移。

   • 如果接受率  太小，则改造马尔可夫链过程中非常容易原地踏步，拒绝大量的跳转。这样使得马尔可夫链遍历所有的状态空间需要花费太长的时间，收敛到平稳分布  的速度太慢。

   • 根据推导  ，如果将系数从 1 提高到  ，则有：

     于是：  。因此，即使提高了接受率，细致平稳条件仍然成立。

4. 将  同比例放大，取： 。

   • 当 时： ，此时满足细致平稳条件。
   • 当 时： ，此时满足细致平稳条件。
   • 当 时： ，此时满足细致平稳条件。

5. MH 算法：

   • 输入：

     • 先验转移概率矩阵
     • 目标分布

   • 输出： 采样出的一个状态序列 

   • 算法：

     • 初始化 

     • 对  执行迭代。迭代步骤如下：

       • 根据  采样出候选样本  ，其中  为转移概率函数。

       • 计算  ：

       • 根据均匀分布从  内采样出阈值 ，如果  ，则接受 ， 即  。否则拒绝  ， 即  。

     • 返回采样得到的序列 

   注意：返回的序列中，只有充分大的  之后的序列  才是服从  分布的采样序列。

3.2 Gibbs 算法

1. MH算法不仅可以应用于一维空间的采样，也适合高维空间的采样。

   对于高维的情况，由于接受率  的存在（通常 ），MH算法的效率通常不够高，此时一般使用 Gibbs 采样算法。

2. 考虑二维的情形：假设有概率分布  ，考察状态空间上  坐标相同的两个点  ，可以证明有：

   于是  。则在  这条平行于  轴的直线上，如果使用条件分布  作为直线上任意两点之间的转移概率，则这两点之间的转移满足细致平稳条件。

   同理：考察  坐标相同的两个点  ， 有  。在  这条平行于  轴的直线上，如果使用条件分布  作为直线上任意两点之间的转移概率，则这两点之间的转移满足细致平稳条件。

   可以构造状态空间上任意两点之间的转移概率矩阵 ： 对于任意两点 ， 令从  转移到  的概率为 ：

   • 如果 ，则 。
   • 如果 ，则 。
   • 否则 。

   采用该转移矩阵  ，可以证明：对于状态空间中任意两点 ，都满足细致平稳条件：

   于是这个二维状态空间上的马尔可夫链将收敛到平稳分布  ，这就是吉布斯采样的原理。

3. Gibbs 算法：

   • 输入：目标分布  ，其中 

   • 输出： 采样出的一个状态序列 

   • 算法步骤：

     • 初始化：随机初始化  。

     • 执行迭代，迭代步骤如下：

       • 随机或者以一定次序遍历索引  。遍历过程为（设当前索引为  ）：

         • 将  保持不变，计算条件概率：  。

           该条件概率就是状态转移概率 

         • 根据条件概率  对分量  进行采样，假设采样结果为  ，则获得新样本  。

         • 令 ，继续遍历。

     • 最终返回一个状态序列  。

4. 吉布斯采样Gibbs sampling 有时被视作MH算法的特例，它也使用马尔可夫链获取样本。