概率论与随机过程

一、概率与分布

1.1 条件概率与独立事件

1. 条件概率：已知 事件发生的条件下 发生的概率，记作 ，它等于事件 的概率相对于事件 的概率，即： 。其中必须有 。

1. 条件概率分布的链式法则：对于  个随机变量 ，有：

2. 两个随机变量  相互独立的数学描述： 。记作：  。

3. 两个随机变量  关于随机变量  条件独立的数学描述： 。

   记作：  。

1.2 联合概率分布

1. 定义 和  的联合分布为： 。

   •  的分布可以从联合分布中得到：

   •  的分布可以从联合分布中得到：

2. 当  和  都是离散随机变量时， 定义  和  的联合概率质量函数为： 

   则  和  的概率质量函数分布为：

3. 当  和  联合地连续时，即存在函数  ，使得对于所有的实数集合  和  满足：

   则函数  称为  和  的概率密度函数。

   • 联合分布为： 。

   •  和  的分布函数以及概率密度函数分别为：

     .

二、期望和方差

2.1 期望

1. 期望描述了随机变量的平均情况，衡量了随机变量  的均值。它是概率分布的泛函（函数的函数）。

   • 离散型随机变量  的期望： 。

     若右侧级数不收敛，则期望不存在。

   • 连续性随机变量  的期望：  。

     若右侧极限不收敛，则期望不存在。

2. 定理：对于随机变量  ，设  也为随机变量， 是连续函数。

   • 若  为离散型随机变量，若  的期望存在，则： 。

     也记做： 。

   • 若  为连续型随机变量，若  的期望存在，则 ： 。

     也记做： 。

   该定理的意义在于：当求  时，不必计算出  的分布，只需要利用  的分布即可。

   该定理可以推广至两个或两个以上随机变量的情况。对于随机变量，假设  也是随机变量，  为连续函数，则有： 。也记做： 。

1. 期望性质：

   • 常数的期望就是常数本身。

   • 对常数  有 ： 。

   • 对两个随机变量 ，有： 。

     该结论可以推广到任意有限个随机变量之和的情况。

   • 对两个相互独立的随机变量，有： 。

     该结论可以推广到任意有限个相互独立的随机变量之积的情况。

2.2 方差

1. 对随机变量  ，若  存在，则称它为  的方差，记作  。

    的标准差为方差的开平方。即：

   • 方差度量了随机变量  与期望值偏离的程度，衡量了  取值分散程度的一个尺度。

   • 由于绝对值  带有绝对值，不方便运算，因此采用平方来计算。

     又因为  是一个随机变量，因此对它取期望，即得  与期望值偏离的均值。

2. 根据定义可知：

3. 对于一个期望为 ， 方差为  的随机变量 ，随机变量  的数学期望为0，方差为1。 称  为  的标准化变量。

4. 方差的性质：

   • 常数的方差恒为 0 。

   • 对常数  ，有  。

   • 对两个随机变量 ，有： 

     当  和  相互独立时，有  。这可以推广至任意有限多个相互独立的随机变量之和的情况。

   •  的充要条件是  以概率1取常数。

2.3 协方差与相关系数

1. 对于二维随机变量  ，可以讨论描述  与  之间相互关系的数字特征。

   • 定义 为随机变量 与 的协方差，记作 。
   • 定义 为随机变量 与的相关系数，它是协方差的归一化。

2. 由定义可知：

3. 协方差的性质：

   • ， 为常数。

4. 协方差的物理意义：

   • 协方差的绝对值越大，说明两个随机变量都远离它们的均值。

   • 协方差如果为正，则说明两个随机变量同时趋向于取较大的值或者同时趋向于取较小的值；如果为负，则说明一个随变量趋向于取较大的值，另一个随机变量趋向于取较小的值。

   • 两个随机变量的独立性可以导出协方差为零。但是两个随机变量的协方差为零无法导出独立性。

     因为独立性也包括：没有非线性关系。有可能两个随机变量是非独立的，但是协方差为零。如：假设随机变量  。定义随机变量  的概率分布函数为：

     定义随机变量 ，则随机变量  是非独立的，但是有：  。

5. 相关系数的物理意义：考虑以随机变量  的线性函数  来近似表示 。以均方误差

   来衡量以  近似表达  的好坏程度。  越小表示近似程度越高。

   为求得最好的近似，则对  分别取偏导数，得到：

   因此有以下定理：

   • （ 是绝对值）。
   • 的充要条件是：存在常数 使得 。

6. 当 较大时，  较小，意味着随机变量  和  联系较紧密。于是  是一个表征 、 之间线性关系紧密程度的量。

7. 当  时，称  和  不相关。

   • 不相关是就线性关系来讲的，而相互独立是一般关系而言的。
   • 相互独立一定不相关；不相关则未必独立。

2.4 协方差矩阵

1. 设  和  是随机变量。

   • 若 存在，则称它为 的 阶原点矩，简称 阶矩。
   • 若 存在，则称它为 的 阶中心矩。
   • 若 存在，则称它为 和 的 阶混合矩。
   • 若 存在，则称它为 和 的 阶混合中心矩。

   因此：期望是一阶原点矩，方差是二阶中心矩，协方差是二阶混合中心矩。

2. 协方差矩阵：

   • 二维随机变量 有四个二阶中心矩（假设他们都存在），记作：

     称矩阵

     为随机变量  的协方差矩阵。

   • 设  维随机变量  的二阶混合中心矩  都存在，则称矩阵

     为  维随机变量  的协方差矩阵。

     由于  因此协方差矩阵是个对称阵。

3. 通常  维随机变量的分布是不知道的，或者太复杂以致数学上不容易处理。因此实际中协方差矩阵非常重要。

三、大数定律及中心极限定理

3.1 切比雪夫不等式

1. 切比雪夫不等式：假设随机变量  具有期望 ， 方差  ，则对于任意正数  ，下面的不等式成立：

   • 其意义是：对于距离  足够远的地方 （距离大于等于  ），事件出现的概率是小于等于 。即事件出现在区间  的概率大于  。

     该不等式给出了随机变量  在分布未知的情况下， 事件  的下限估计。如：  。

   • 证明：

2. 切比雪夫不等式的特殊情况：设随机变量  相互独立，且具有相同的数学期望和方差： 。 作前  个随机变量的算术平均： ， 则对于任意正数  有：

   证明：根据期望和方差的性质有：，  。根据切比雪夫不等式有：

   则有  ，因此有： 。

3.2 大数定理

1. 依概率收敛：设  是一个随机变量序列，  是一个常数。

   若对于任意正数  有 ：  ，则称序列  依概率收敛于  。记作： 

2. 依概率收敛的两个含义：

   • 收敛：表明这是一个随机变量序列，而不是某个随机变量；且序列是无限长，而不是有限长。
   • 依概率：表明序列无穷远处的随机变量 的分布规律为：绝大部分分布于点 ，极少数位于 之外。且分布于 之外的事件发生的概率之和为0。

3. 大数定理一： 设随机变量  相互独立，且具有相同的数学期望和方差： 。 则序列：  依概率收敛于  ， 即  。

   注意：这里并没有要求随机变量  同分布。

4. 伯努利大数定理： 设  为  次独立重复实验中事件  发生的次数，  是事件  在每次试验中发生的概率。则对于任意正数  有：

   即：当独立重复实验执行非常大的次数时，事件  发生的频率逼近于它的概率。

5. 辛钦定理：设随机变量  相互独立，服从同一分布，且具有相同的数学期望： 。 则对于任意正数  有：

   • 注意：这里并没有要求随机变量 的方差存在。
   • 伯努利大数定理是亲钦定理的特殊情况。

3.3 中心极限定理

1. 独立同分布的中心极限定理：设随机变量  独立同分布，且具有数学期望和方差： ， 则随机变量之和  的标准变化量：

   的概率分布函数  对于任意  满足：

   • 其物理意义为：均值方差为  的独立同分布的随机变量  之和  的标准变化量 ，当  充分大时，其分布近似于标准正态分布。

     即： 在  充分大时，其分布近似于  。

   • 一般情况下，很难求出  个随机变量之和的分布函数。因此当  充分大时，可以通过正态分布来做理论上的分析或者计算。

2. Liapunov 定理：设随机变量  相互独立，具有数学期望和方差： 。记：。 若存在正数 ，使得当  时， 。则随机变量之和  的标准变化量:

   的概率分布函数  对于任意  满足：

   • 其物理意义为：相互独立的随机变量 之和 的衍生随机变量序列，当 充分大时，其分布近似与标准正态分布。
   • 这里并不要求 同分布。

1. Demoiver-Laplace定理：设随机变量序列  服从参数为  的二项分布，其中  。则对于任意  , 有：

   该定理表明，正态分布是二项分布的极限分布。当  充分大时，可以利用正态分布来计算二项分布的概率。

五、常见概率分布

5.1 均匀分布

1. 离散随机变量的均匀分布：假设  有  个取值： ，则均匀分布的概率密度函数(probability mass function:PMF)为：

2. 连续随机变量的均匀分布： 假设  在 [a,b]上均匀分布，则其概率密度函数(probability density function：PDF)为：

   .

5.2 伯努利分布

1. 伯努利分布：参数为 。随机变量  。

   • 概率分布函数为： 。
   • 期望： 。方差： 。

2. categorical 分布：它是二项分布的推广，也称作multinoulli分布。假设随机变量 ，其概率分布函数为：

   其中  为参数，它满足 ，且  。

5.3 二项分布

1. 假设试验只有两种结果：成功的概率为 ，失败的概率为 。 则二项分布描述了：独立重复地进行  次试验中，成功  次的概率。

   • 概率质量函数：

   • 期望： 。 方差：  。

5.4 高斯分布

1. 正态分布是很多应用中的合理选择。如果某个随机变量取值范围是实数，且对它的概率分布一无所知，通常会假设它服从正态分布。有两个原因支持这一选择：

   • 建模的任务的真实分布通常都确实接近正态分布。中心极限定理表明，多个独立随机变量的和近似正态分布。
   • 在具有相同方差的所有可能的概率分布中，正态分布的熵最大（即不确定性最大）。

5.4.1 一维正态分布

1. 正态分布的概率密度函数为 :

   其中  为常数。

   • 若随机变量 的概率密度函数如上所述，则称 服从参数为 的正态分布或者高斯分布，记作 。
   • 特别的，当 时，称为标准正态分布，其概率密度函数记作 ，分布函数记作 。
   • 为了计算方便，有时也记作： ，其中 。

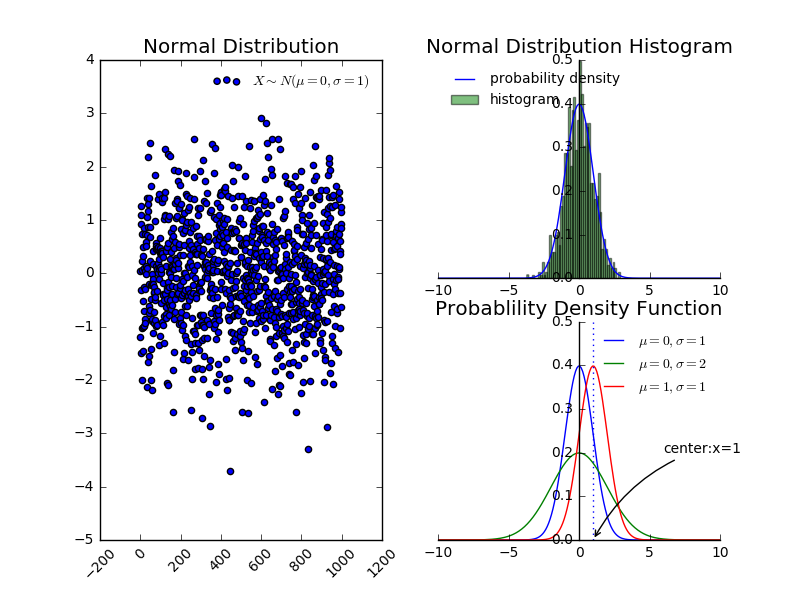
2. 正态分布的概率密度函数性质：

   • 曲线关于 对称。
   • 曲线在 时取最大值。
   • 曲线在 处有拐点。
   • 参数 决定曲线的位置； 决定图形的胖瘦。

   

3. 若  则：

   • 期望： 。方差： 。

4. 有限个相互独立的正态随机变量的线性组合仍然服从正态分布：若随机变量  且它们相互独立，则它们的线性组合： 仍然服从正态分布（其中 不全是为 0 的常数），且： 。