目录
一、引言
二叉树是一种常见的数据结构,它由节点组成,每个节点最多有两个子节点。二叉树在计算机科学中有广泛的应用,如搜索、排序、树状结构的表示等。
关于二叉树的知识点和代码都比较多,因此我会分几个篇幅介绍,本章将介绍普通二叉树的基本操作,包括结构体,遍历二叉树,创建二叉树,数据查找,判断树的深度等,代码的逻辑以递归为主。🥰
二、二叉树中的一些名词
-
树的深度:空树深度为0,树的根节点深度为1,每往下一层深度加一;
-
叶子节点:左右子树为0的节点称为叶子节点,很多情况下只有叶子节点存放有效数据
-
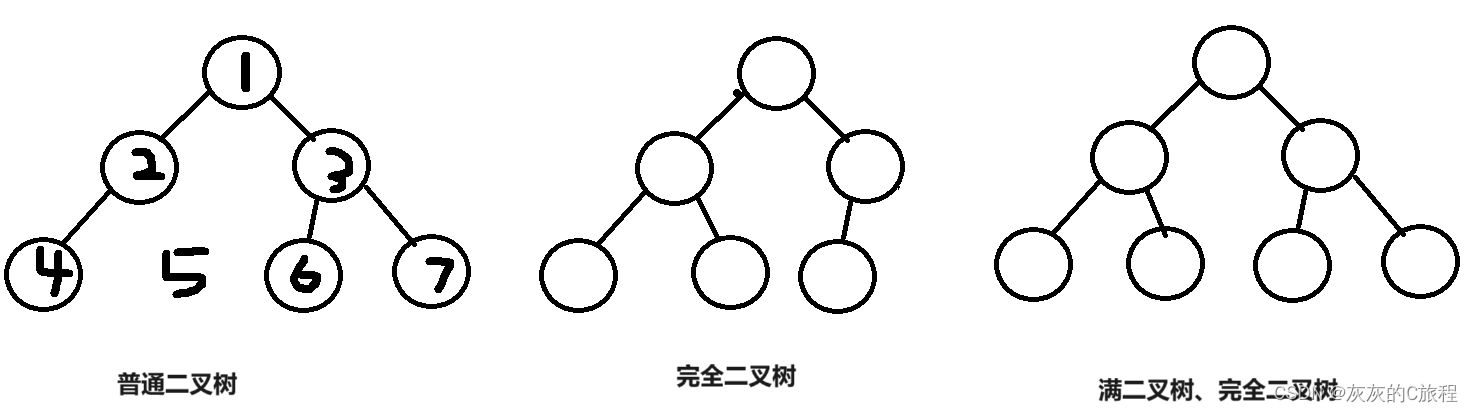
满二叉树:只有最深的一层有叶子节点;
-
完全二叉树:可以理解为从上到下,从左到右依次给节点编号,节点之间的编号必须是连续的,不能中断
三、二叉树的作用
树作为我们新学习的数据结构,我们首先要知道它有什么优势,在什么情况下使用,而不能像无头苍蝇一样只学会了怎么用,但是又从来没有使用过,到最后忘得一干二净。要合理使用二叉树,我们应该先了解一下它的优点有哪些:
二叉树的优点:
1、搜索效率高:对于有序的二叉树,搜索操作的时间复杂度为,比顺序搜索快得多(因为我们只需要朝左节点或右节点访问,选择一次数据就少一半)。
2、插入和删除操作相对简单:在某些情况下,二叉树的插入和删除操作比其他数据结构更容易实现。
✨二叉树的应用场景:
最常见的是海量数据并发查询,二叉树复杂度是。二叉排序树就既有链表的好处,也有数组的好处, 在处理大批量的动态的数据是比较有用。
此外还有哈夫曼编码,用于压缩存储,提高数据传输的效率、红黑树等等都需要使用到二叉树,以后有机会再进行分享~
四、C代码实现
1、结构体定义
typedef struct BinTree{
ElemType data; //数据域
struct BinTree *lchile; //左右子树
struct BinTree *rchile;
char* flag; //Huffman编码,这个暂时用不上
}BinTree;
2、✨树的遍历方式✨
树有四种遍历方式,分别是前序遍历,中序遍历,后序遍历和层序遍历,其遍历顺序入下图:
前序遍历:

前序遍历是从根节点开始一直朝左子树访问到底,若左子树为空则返回访问右子树
中序遍历:

节点左边的节点一定在左子树,节点右边的节点一定在右子树
后序遍历:

层序遍历(使用队列)

㊙️截图来自b站up主:鱼C-小甲鱼,小污龟的数据结构的视频讲的还是挺好的,推荐大家去康康
1)使用递归实现:
用递归实现遍历其代码基本相同,根据需要的顺序改变递归函数的顺序即可。
//二叉树先序遍历算法 - 根 左 右
int PreOrderTraverse(BinTree* T) {
if (T == NULL) { //结束递归的条件
return 1;
}
else {
visit(T); //访问该节点
PreOrderTraverse(T->lchile); //遍历递归左子树
PreOrderTraverse(T->rchile); //遍历递归右子树
}
}
//二叉树中序遍历算法 - 左 根 右
int InOrderTraverse(BinTree* T) {
if (T == NULL) {
return 1;
}
else {
InOrderTraverse(T->lchile); //遍历递归左子树
visit(T); //访问该节点
InOrderTraverse(T->rchile); //遍历递归右子树
}
}
//二叉树后序遍历算法 - 左 右 根
int PostOrderTraverse(BinTree* T) {
if (T == NULL) {
return 1;
}
else {
PostOrderTraverse(T->lchile); //遍历递归左子树
PostOrderTraverse(T->rchile); //遍历递归右子树
visit(T); //访问根节点
}
}
当然还有很多方法实现树的遍历,比如借用队列,栈来遍历也是很好的方法(这就成功把前面的知识应用起来了)但是篇幅有限,我们会在下一篇文章中讲解。
2)使用栈先序遍历
3)使用队列层序遍历
3、✨树的创建✨
/*
* @brief 通过字符数组递归创建一棵树
* @param 节点地址,节点字符串
* @return None
*/
void Tree_Creative_ARR(BinTree** root,char* str,int* i)
{
if (*root == NULL) return;
char c;
c = str[*i];
if (c == ' ')
{
*root = NULL;
}
else
{
*root = (BinTree*)malloc(sizeof(BinTree));
(*root)->data = c;
memset((*root)->flag, 0, 5);
(*i)++;
Tree_Creative_ARR(&(*root)->lchile, str, i);
(*i)++;
Tree_Creative_ARR(&(*root)->rchile, str, i);
}
return;
}
//调用:需要一个值为0的int指针
int i = 0;
Tree_Creative_ARR(&T,str,&i);
-
这里使用前序遍历的方法输入二叉树的数据;
-
空格表示空子树,因此在遇到叶子节点时后面要跟上两个空格,比如上面先序遍历的图其字符串应该为abdh()()i()()e()j()()cf()k()()g()() ;
-
通过这种方法创建的二叉树是一个普通(无序)二叉树;(有序二叉树后面也会讲到)
4、✨数据的查找
对于普通二叉树,其数据存放是无序的,需要使用遍历的方法查找
/*
* @brief 在二叉树中查找
* @param 根节点,要查找的数据
* @return 该节点的指针
*/
BinTree* Tree_Find(BinTree* root, ElemType x)
{
if (root == NULL) return NULL;
if (root->data == x)return root;
BinTree* t;
t = Tree_Find(root->lchile, x);
if (t != NULL)return t;
t = Tree_Find(root->rchile, x);
if (t != NULL)return t;
return NULL;
}
5、求二叉树的深度
//输出树的深度(根的深度为1)
int Tree_Depth(BinTree* T)
{
int n, m;
if (T == NULL)
return 0; //如果是空树,深度为0,递归结束
else
{
n = Tree_Depth(T->lchile); //递归计算左子树的深度记为n
m = Tree_Depth(T->rchile); //递归计算右子树的深度记为m
if (m > n)
return (m + 1);
else
return (n + 1);
}
}
由于树特殊的结构类型,在配合栈或队列时食用效果更佳!这将会在下一篇文章中介绍🥰
最后感谢你观看完我的文章,如果文章对你有帮助,可以点赞收藏评论,这是对作者最好的鼓励!不胜感激🥰

























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








