Java实现数据结构---红黑树_java 红黑树-优快云博客

本文深入解析红黑树的定义、特性、节点与类定义、旋转操作、插入与删除算法及其实现细节。通过代码示例展示红黑树的平衡调整过程，包括插入后的旋转调整和删除后的平衡恢复。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

文章目录

红黑树的定义
节点类定义
红黑树类定义
左旋与右旋
红黑树的插入
红黑树删除
红黑树遍历
测试
完成代码

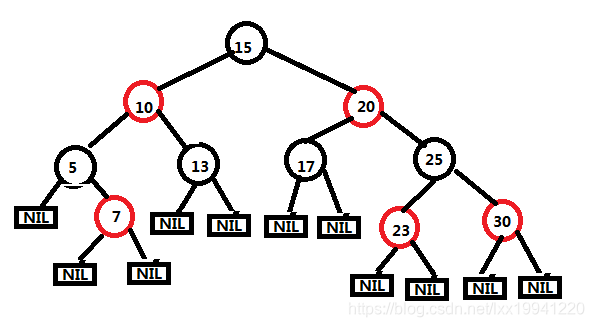
红黑树的定义

红黑树是一种自平衡树，它也是一颗二叉树。它和AVL树比较类似，在插入、删除过程中不平衡的话，也会进行旋转操作，红黑树主要有以下五个特性：

节点的颜色为红色或者黑色；
根节点为黑色；
所有的叶子节点为黑色，叶子是NIL节点，也就是NULL节点；
如果一个节点是红色节点，那么他的左右子节点必须为黑色；
从根节点到任意叶子节点的所有简单路径都包含数量相同的黑色节点。

根据红黑树的五大特点可以看出，红黑树虽然还是平衡树（由特点5可以看出红黑树的平衡条件是：任意节点的左右子树高度差不能超过2倍减一，例如：相同4个黑色节点，那么最小路径就是4个黑色节点，最多就是4个黑色节点之间交叉着3个红色节点一共7个节点），但并不像AVL树那样绝对平衡（任意节点的左右子树高度差不能大于1），相比于AVL树，红黑树减少了树旋转调整的次数，插入删除效率比AVL树更高，查找效率略低于AVL树，达到了插入查找效率的平衡点，这也是红黑树应用十分广泛的原因。
在这里插入图片描述

节点类定义

红黑树节点中，除了像AVL树有左子节点、右子节点、数据项、父节点外，还有一个颜色属性，设置为Boolean类型，True代表红色，False代表黑色。代码如下：

package com.xxliao.datastructure.tree.read_black_tree;

/**
 * @author xxliao
 * @description: 红黑树节点类实现
 * @date 2024/5/29 0:42
 */
public class Node {
    //存储数据,int方便实现
    public int data;
    //左子节点
    public Node left;
    //右子节点
    public Node right;
    //父节点
    public Node parent;
    //红色,color为true
    public static final boolean RED = true;
    //黑色,color为true
    public static final boolean BLACK = false;
    //颜色初始为黑色,红黑树新增时改为红色
    public boolean color = BLACK;

    //构造方法
    Node(int data, Node parent) {
        this.data = data;
        this.parent = parent;
        left = null;
        right = null;
        color = RED;
    }
}

红黑树类定义

红黑树类中跟AVL树一样，记录根节点，以及元素个数属性。代码如下：

package com.xxliao.datastructure.tree.read_black_tree;
/**
 * @author xxliao
 * @description: 红黑树实现类
 * @date 2024/5/29 0:43
 */
public class RedBlackTree {

    // 根节点
    public Node root;
    // 元素个数
    public int size;

    // 构造方法
    public RedBlackTree() {
        root = null;
        size = 0;
    }

    // 判断是否为空
    public boolean isEmpty() {
        return (root == null);
    }
    // 获取元素个数
    public int size() {
        return size;
    }
    // 获取根节点
    public Node getRoot() {
        return root;
    }
    // 获取节点颜色
    private static boolean colorOf(Node p) {
        return (p == null ? Node.BLACK : p.color);
    }
    // 获取节点父节点
    private static Node parentOf(Node p) {
        return (p == null ? null : p.parent);
    }
    // 设置节点颜色
    private static void setColor(Node p, boolean c) {
        if (p != null)
            p.color = c;
    }
    // 获取节点左子节点
    private static Node leftOf(Node p) {
        return (p == null) ? null : p.left;
    }
    // 获取节点右子节点
    private static Node rightOf(Node p) {
        return (p == null) ? null : p.right;
    }
}

左旋与右旋

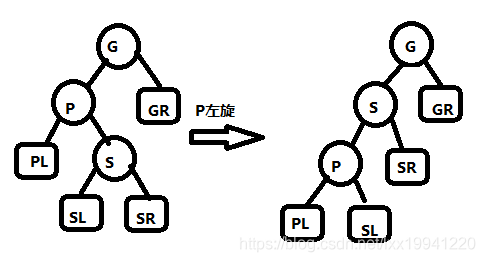
左旋
节点左旋,旋转节点的右子节点会作为旋转节点的父节点,旋转节点的右子节点变为原右子节点的左子节点。变化过程如图所示：

左旋代码实现:

// 节点左旋：以节点的右子节点为轴，进行左旋
private void rotateLeft(Node p) {
    if (p != null) {
        // 记录节点的右子节点
        Node s = p.right;
        // 右子节点的左节点 换到 旋转节点的 右子节点
        p.right = s.left;
        
        if (s.left != null)// 右子节点有左子节点（不为空，上面已经成p的右子节点了），指定父节点为p节点
            s.left.parent = p;
        // 替换节点 顶替 旋转节点，指定替换节点的新父类
        s.parent = p.parent;
        if (p.parent == null)
            // 旋转节点是否为根节点判断
            root = s;
        else if (p.parent.left == p)
            // 旋转节点为父节点的左子节点,父节点的左子节点绑定为旋转节点的原右子节点
            p.parent.left = s;
        else
            // 旋转节点为父节点的右子节点,父节点的右子节点绑定为旋转节点的原右子节点
            p.parent.right = s;
        // r与P绑定
        s.left = p;
        p.parent = s;
    }
}

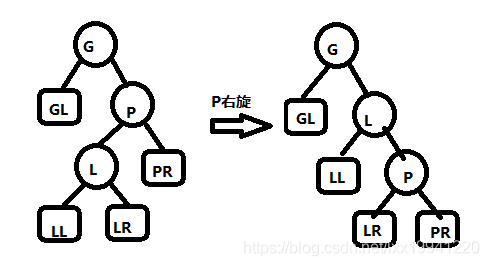
右旋
节点右旋,旋转节点的左子节点会作为旋转节点的父节点,旋转节点的左子节点变为旋转原左子节点的右子节点。变化过程如图所示：

右旋代码实现：

// 节点右旋 ,以节点的左子节点为轴，进行右旋
private void rotateRight(Node p) {
    if (p != null) {
        // 记录旋转节点的左子节点，替换节点
        Node l = p.left;
        // 左子节点的右子节点 换到 旋转节点的左子节点
        p.left = l.right;
        if (l.right != null)
            // 旋转节点原左子节点的右子节点存在，与旋转节点绑定
            l.right.parent = p;
        // 旋转节点原左子节点替换旋转节点
        l.parent = p.parent;
        if (p.parent == null)
            // 旋转节点是为根节点判断
            root = l;
        else if (p.parent.right == p)
            // 旋转节点为父节点的右子节点，父节点右子节点指向新的l节点
            p.parent.right = l;
        else
            // 旋转节点为父节点的左子节点，父节点左子节点指向新的l节点
            p.parent.left = l;
        // l和p相互绑定
        l.right = p;
        p.parent = l;
    }
}

红黑树的插入

红黑树因为特性5的原因，一个平衡状态的红黑树新插入黑色节点一定会造成树不平衡，因此红黑树的插入节点默认为红色节点，红黑树的插入主要分为5种情况：

红黑树为空，新插入节点
（1）插入节点直接作为根节点，因为违反特性2，所以插入节点颜色变为黑色，插入完毕。
插入节点的父节点为黑色
（1）不违反任何特性，直接插入即可；
N为红、P（N的父节点）为红、U（N的叔叔节点）为红、G（祖父节点）一定为黑
（1）这里不需要考虑N是P的左子节点还是右子节点，也不需要考虑P节点是G节点的左子节点还是右子节点。将P、U节点改为黑色，G节点改为红色，如果G的父节点为黑色，插入结束；如果G的父节点为红，就继续以G节点作为起始点继续向上回溯，直到回溯中途变换后满足红黑树特性或者回溯到根节点，根节点满足为黑色结束。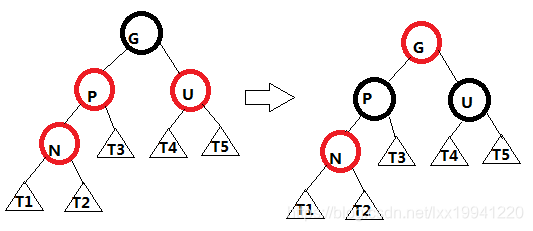
N为红、P（N的父节点）为红、U（N的叔叔节点）为黑、G（祖父节点）为一定为黑色节点，LL情况以及RR情况。
（1） P为G的左子节点，N为P的左子节点，P和G交换颜色，再将G节点右旋。
（2） P为G的右子节点，N为P的右子节点，P和G交换颜色，再将G节点左旋。
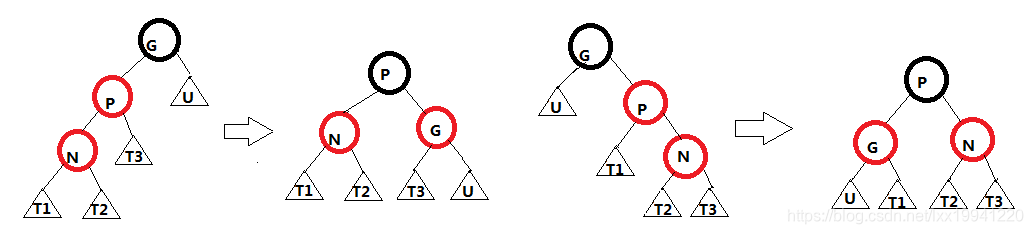
N为红、P（N的父节点）为红、U（N的叔叔节点）为黑、G（祖父节点）为一定为黑色节点,LR情况以及RL情况。
（1） P为G的左子节点，N为P的右子节点，将P节点左旋，形成LL情况，然后N和G交换颜色，再将G节点右旋。
（2） P为G的右子节点，N为P的左子节点，将P节点右旋，形成RR情况，然后N和G交换颜色，再将G节点左旋。

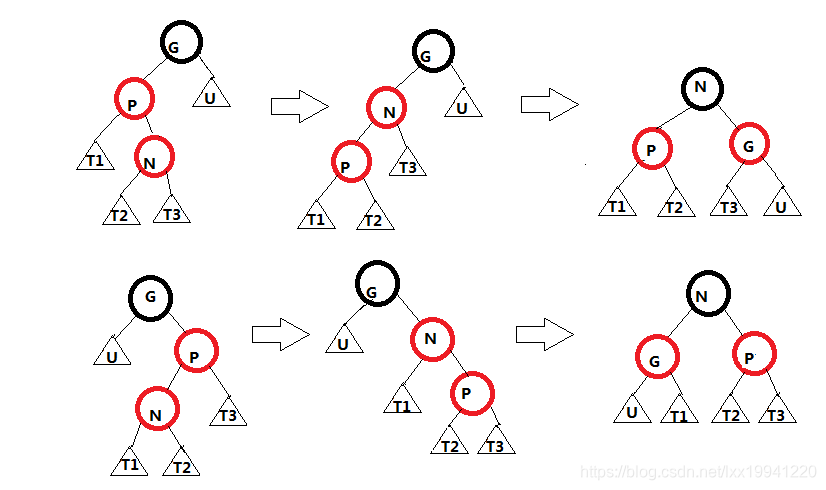
插入代码如下：

// 新增后调整红黑树平衡
private void fixAfterInsertion(Node newNode) {
    // 新增节点颜色默认为红色
    // 新增时,只有新增节点的父节点为红色,才需要调整,并且新增节点不是根节点
    while (newNode != null && newNode != root && colorOf(parentOf(newNode)) == Node.RED) {
        if (parentOf(newNode) == leftOf(parentOf(parentOf(newNode)))) {
            // 新增节点的父节点是祖父节点的左子节点
            // 获取叔叔节点
            Node s = rightOf(parentOf(parentOf(newNode)));
            if (colorOf(s) == Node.RED) {
                // 叔叔节点为红色,满足父节点红色,叔叔节点红色,祖父节点黑色情况,
                // 将父节点以及兄弟节点变为黑色,祖父节点变为红色
                setColor(parentOf(newNode), Node.BLACK);
                setColor(s, Node.BLACK);
                setColor(parentOf(parentOf(newNode)), Node.RED);
                // 祖父节点作为新增节点,继续向上回溯
                newNode = parentOf(parentOf(newNode));
            } else {
                // 叔叔节点为黑色
                if (newNode == rightOf(parentOf(newNode))) {
                    // 新增节点是父节点的右子节点,也就是LR情况,需要先旋转为LL情况
                    newNode = parentOf(newNode);
                    // 注意这里是新增节点的父节点左旋,然后newNode变量就会变成LL情况下的新增节点
                    rotateLeft(newNode);
                }
                // 新增节点是父节点的左子节点,也就是LL情况,右旋祖父节点,父节点和祖父节点颜色交换
                setColor(parentOf(newNode), Node.BLACK);
                setColor(parentOf(parentOf(newNode)), Node.RED);
                rotateRight(parentOf(parentOf(newNode)));
            }
        } else {
            // 新增节点的父节点是祖父节点的右子节点
            // 获取叔叔节点
            Node s = rightOf(parentOf(parentOf(newNode)));
            if (colorOf(s) == Node.RED) {
                // 叔叔节点是红色,父节点是红色,新增节点是红色
                setColor(parentOf(newNode), Node.BLACK);
                setColor(s, Node.BLACK);
                setColor(parentOf(parentOf(newNode)), Node.RED);
                // 祖父节点作为新增节点,继续向上回溯
                newNode = parentOf(parentOf(newNode));
            } else {
                // 叔叔节点是黑色
                if (newNode == leftOf(parentOf(newNode))) {
                    // 新增节点为父节点的左子节点.满足RL情况,先旋转为RR情况
                    newNode = parentOf(newNode);
                    // 注意这里是新增节点的父节点左旋,然后newNode变量就会变成RR情况下的新增节点
                    rotateRight(newNode);
                }
                // 满足RR情况,将父节点设置为黑色,祖父节点设置为红色,然后祖父节点左旋
                setColor(parentOf(newNode), Node.BLACK);
                setColor(parentOf(parentOf(newNode)), Node.RED);
                rotateLeft(parentOf(parentOf(newNode)));
            }
        }
    }
    root.color = Node.BLACK;
}

红黑树删除

红黑树的5大特性：

节点的颜色为红色或者黑色；
根节点为黑色；
所有的叶子节点为黑色，叶子是NIL节点，也就是NULL节点；
如果一个节点是红色节点，那么他的左右子节点必须为黑色；
从根节点到任意叶子节点的所有简单路径都包含数量相同的黑色节点。

红黑树的删除，用一般二叉树的删除角度来看，可能分为3种情况：

情况一：删除节点为叶子节点（非NIL或者NULL节点）
1. 叶子节点为红色
  当删除叶子节点（D）为红色，其父节点（P）根据特性4必然为黑色，这种情况下直接删除红色叶子节点，符合特性5（红节点不计入黑高度），也不违背红黑树其他特性，删除完毕。
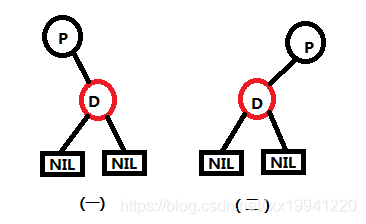
2. 叶子节点为黑色：
  我们约定 D为待删除的结点，P 为 D 的父结点，S 为 D 的兄弟节点，SL、SR 分别为S的左子节点以及右子节点；当D为P的左子节点时，SL为近侄子节点，SR为远侄子节点；当D为P的右子节点时，SR为近侄子节点，SL为远侄子节点。
  
  (1) 父节点P为红色
  
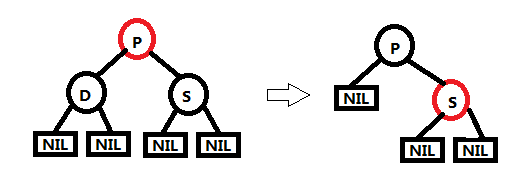
  删除节点D为黑色，父节点P为红色，根据红黑树的特性，兄弟节点S必然为黑色，SL、SR必然为NIL节点。
  操作：这种情况下删除节点D后，只需要将父节点P颜色变为黑色，然后兄弟节点S颜色变为红色，图中D节点删除前P树的黑高度为2，删除后P树的黑高度仍为2，删除完毕。
  
  (2) 父节点P为黑色，兄弟节点S为黑色，兄弟节点S没有子节点
  
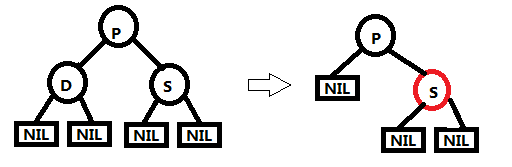
  删除节点D为黑色，父节点P以及兄弟节点S为黑色，SL、SR为NIL节点。
  操作：这种情况下删除节点D后，先将兄弟节点S变为黑色，因为图中D节点删除前P树的黑高度为3、删除后P树的黑高度为2，所以要从P节点继续向上回溯调整树节点，直至树平衡。
  
  (3) 父节点P为黑色，兄弟节点S为红色
  
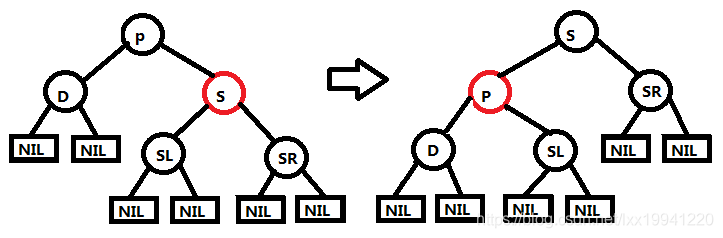
  当删除节点D为父节点P的左子节点时，树如上图所示。
  操作：将父节点P与兄弟节点S颜色互换，然后P节点左旋，即可得到图右树，也就形成了情况（1），删除节点父节点为红色的情况，根据情况（1）修改方法修改即可。
  
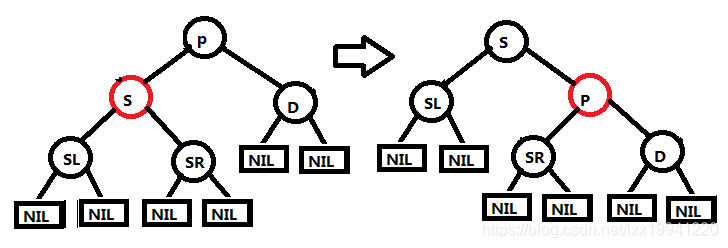
  当删除节点D为父节点P的右子节点时，树如上图所示。
  操作：将父节点P与兄弟节点S颜色互换，然后P节点右旋，即可得到图右树，也就形成了情况1（删除节点父节点为红色的情况），根据情况1修改方法修改即可。
  
  (4) 兄弟节点S为黑色，远侄子节点为红色
  
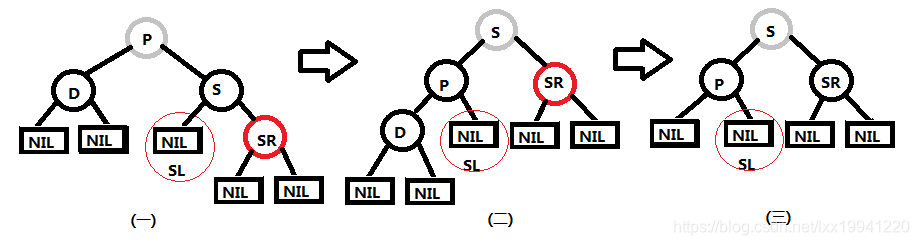
  当删除节点D为父节点P的左子节点，那么节点D的远侄子节点为SR，根据红黑树特性，节点D的近侄子节点SL为NIL节点，具体如上图(一)所示。
  操作：将父节点P与兄弟节点S互换颜色，然后将父节点P左旋，形成图(二)，然后删除节点D，将原节点D的远侄子节点SR颜色变为黑色，形成图(三)，删除完毕。
  注：图(一)中节点P的颜色与图(三)中的S节点颜色相同，并且图(一)中节点P的黑高度与图(三)中节点S的黑高度相等，相当于变换是在树中进行。
  
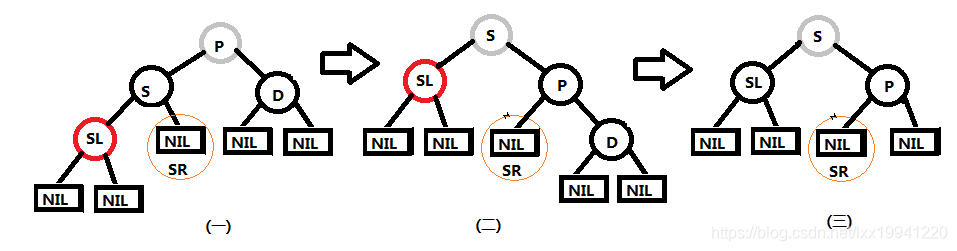
  当删除节点D为父节点P的右子节点，那么节点D的远侄子节点为SL，根据红黑树特性，节点D的近侄子节点SR为NIL节点，具体如上图(一)所示。
  操作：将父节点P与兄弟节点S互换颜色，然后将父节点P右旋，形成图(二)，然后删除节点D，将原节点D的远侄子节点SR颜色变为黑色，形成图(三)，删除完毕。
  
  (5) 兄弟节点S为黑色，近侄子节点为红色
  
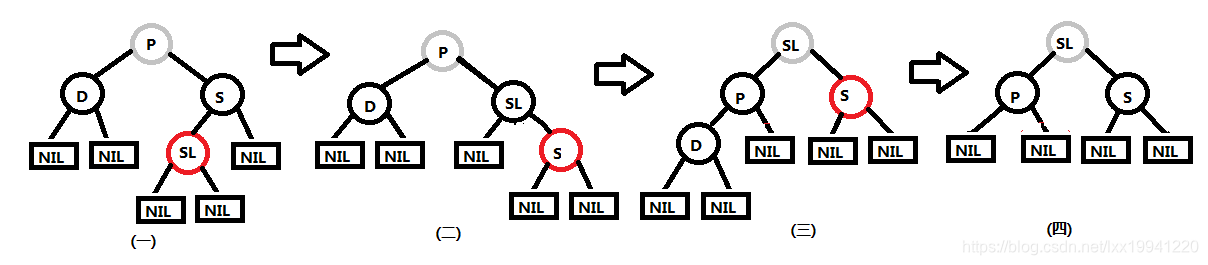
  当删除节点D为父节点P的左子节点时，那么节点D的近子节点为SL，根据红黑树特性，节点D的远子节点SR为NIL节点，具体如图(一)所示。
  操作：将节点D的兄弟节点S与近子节点SL颜色互换，然后对兄弟节点进行右旋，形成图(二)，然后该红黑树就会变成情况(4)的情况，然后按照情况(4)的解决办法，依次形成图(三)、图(四)。
  
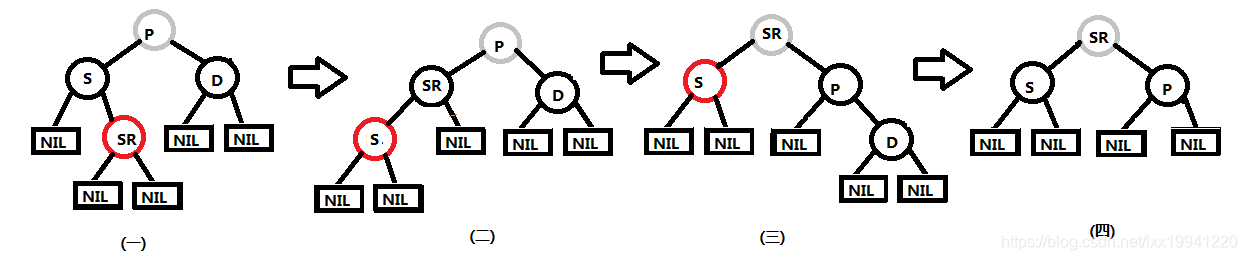
  当删除节点D为父节点P的右子节点时，那么节点D的近子节点为SR，根据红黑树特性，节点D的远子节点SL为NIL节点，具体如图(一)所示。
  操作：将节点D的兄弟节点S与近子节点SR颜色互换，然后对兄弟节点进行左旋，形成图(二)，然后该红黑树就会变成情况(4)的情况，然后按照情况(4)的解决办法，依次形成图(三)、图(四)。
  
  (6) 兄弟节点S为黑色，远、近侄子节点均为红色。
  
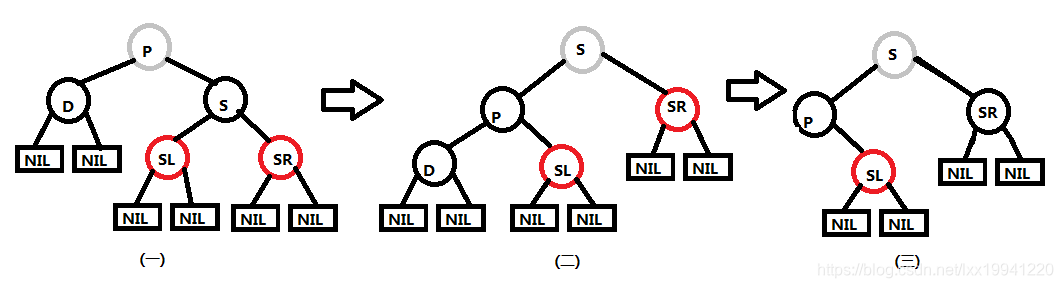
  当删除节点D为父节点P的左子节点时，情形如图(一)。
  操作：先将父节点P与兄弟节点S颜色互换，然后父节点P左旋形成图(二)，然后删除节点D，将删除节点D的原远子节点SR颜色变为黑色，删除完毕。
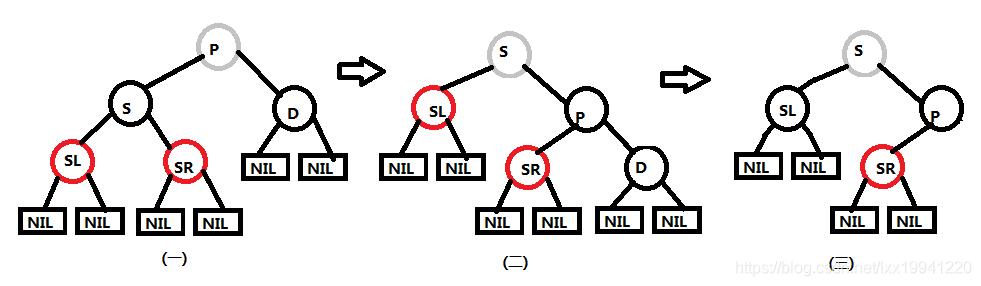  当删除节点D为父节点P的右子节点时，情形如图(一)。
  操作：先将父节点P与兄弟节点S颜色互换，然后父节点P右旋形成图(二)，然后删除节点D，将删除节点D的原远子节点SL颜色变为黑色，删除完毕。
情况二：删除节点(D)只有左子树(DL)或者右子树(DR)
1. 黑+黑、红+黑不存在
  
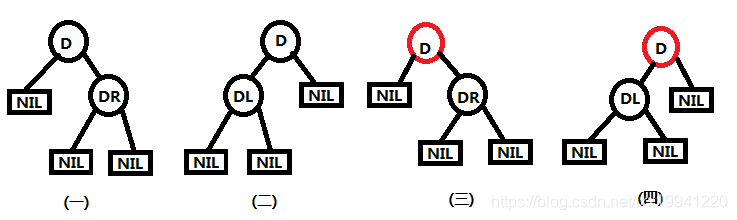
  上面图一到图四中，对于删除节点D来说，左右子树的黑高度明显不一致，根节点到删除节点的黑高度是固定的，根据红黑树特性5规定，所以“黑+黑”、“红+黑”情况不存在。
2. 黑+红存在
  
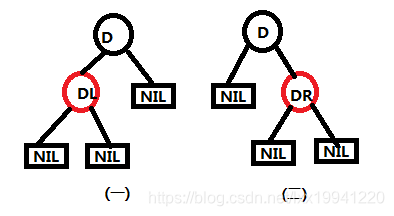
  上面图一以及图二就是“黑+红”存在的两种情况，只需要直接删除D节点，然后用DL、DR替换原D位置，颜色变为黑色即可，删除完毕。
情况三：删除节点既有左子树又有右子树
- 删除既有左子树又有右子树的节点，首先要找到删除节点的替代节点，然后用替换节点的数据替换删除节点的数据，颜色保持原删除节点的颜色，然后真正需要删除的是替换节点（根据替换原理，要么替换节点为叶子节点，要么替换节点只有一个子树），于是情况三变成了情况一或者情况二。
删除代码如下：

// 删除操作
 public boolean remove(int data) {
     if (root == null) {
         // 空树
         return false;
     }
     // 查找删除数据节点
     Node deleteNode = root;
     while (deleteNode.data != data) {
         if (data < deleteNode.data) {
             // 小于,继续左子树查找
             deleteNode = deleteNode.left;
         } else if (data > deleteNode.data) {
             // 大于,继续右子树查找
             deleteNode = deleteNode.right;
         }
         if (deleteNode == null) {
             // 不存在删除数据的节点
             return false;
         }
     }
     // 找到节点,开始删除，后面删除的结构就变成了 叶子节点了
     if (deleteNode.left != null && deleteNode.right != null) {
         // 删除节点存在左右子节点,找出替代节点,数据替换,然后删除节点为替换节点
         Node temp = successor(deleteNode);
         deleteNode.data = temp.data;
         deleteNode = temp;
     }
     // 到达这里的删除节点要么为叶子节点,要么为只有一个子节点的节点，两个节点都有的上面if已经替换过了
     if (deleteNode == root) {
         // 删除节点为根节点
         root = null;
         return true;
     }
     // 定义删除后,上移位置的子节点
     Node replaceNode = (deleteNode.left != null ? deleteNode.left : deleteNode.right);
     if (replaceNode == null) {
         // 删除节点为叶子节点
         if (deleteNode.color == Node.BLACK) {
             // 叶子节点为黑色,旋转变换
             fixAfterDeletion(deleteNode);
         }
         if (deleteNode.parent != null) {
             // 删除叶子节点，存在父节点
             if (deleteNode == deleteNode.parent.left) {
                 // 删除节点为父节点的左子节点
                 deleteNode.parent.left = null;
             } else {
                 // 删除节点为父节点的右子节点
                 deleteNode.parent.right = null;
             }
         }
     } else {
         // 删除节点为只有一个子节点的节点，黑+黑，红+黑不存在，只有黑+红存在（因为这里删除的是替换后的叶子节点，根据红黑树特性，只有黑+红），
         // 直接删除黑色节点，然后红色节点上移补充黑色节点位置，然后将颜色变为黑色
         replaceNode.parent = deleteNode.parent;
         if (deleteNode.parent == null) {
             // 是否为根节点判断
             root = replaceNode;
         } else if (deleteNode == deleteNode.parent.left) {
             // 删除节点为父节点的左子节点
             deleteNode.parent.left = replaceNode;
         } else {
             // 删除节点为父节点的右子节点
             deleteNode.parent.right = replaceNode;
         }
         deleteNode.left = deleteNode.right = deleteNode.parent = null;

         /*
          * if (deleteNode.color == Node.BLACK) //黑+
          * 红，红色节点替换黑色节点后，颜色变换,在执行fixAfterDeletion时不会进入while循环，只是设置颜色
          * fixAfterDeletion(replaceNode);
          */
         replaceNode.color = Node.BLACK;
     }
     return true;
 }

 // 删除前调整红黑树
 private void fixAfterDeletion(Node deleteNode) {
     // 删除节点为红色节点时,直接删除,不需要调整平衡
     while (deleteNode != root && deleteNode.color == Node.BLACK) {
         if (deleteNode == leftOf(leftOf(parentOf(deleteNode)))) {
             // 删除节点为父节点的左子节点
             // 获取兄弟节点
             Node s = rightOf(parentOf(deleteNode));
             if (colorOf(s) == Node.RED) {
                 // 兄弟节点是红色，那么父亲节点为黑色，远近侄子节点均为黑色，兄弟节点颜色互换，父节点左旋
                 setColor(s, Node.BLACK);
                 setColor(parentOf(deleteNode), Node.RED);
                 rotateLeft(deleteNode.parent);
                 // 新的兄弟节点变为新父节点的柚子节点
                 s = rightOf(parentOf(deleteNode));
             }
             // 执行到这里代表，删除节点为黑色，兄弟节点为黑色

             if (colorOf(leftOf(s)) == Node.BLACK && colorOf(rightOf(s)) == Node.BLACK) {
                 // 删除节点的两个子节点均为黑色，将兄弟节点设置为红色
                 setColor(s, Node.RED);
                 deleteNode = parentOf(deleteNode);
             } else {
                 if (colorOf(leftOf(s)) == Node.RED) {
                     // 近侄子节点为红色，先将近侄子节点与兄弟节点颜色互换，然后兄弟节点右旋，转化为远子节点为红色情况。
                     setColor(leftOf(s), Node.BLACK);
                     setColor(s, Node.RED);
                     rotateRight(s);
                     // 记录新的兄弟节点
                     s = rightOf(parentOf(deleteNode));
                 }
                 // 执行到这里为远侄子节点为红色情况，父节点颜色与星弟节点互换，远侄子节点变为黑色，然后父节点左旋
                 setColor(s, colorOf(parentOf(deleteNode)));
                 setColor(parentOf(deleteNode), Node.BLACK);
                 setColor(rightOf(s), Node.BLACK);
                 rotateLeft(deleteNode.parent);
                 // 树已经平衡，这里等于root是为了保证root的颜色，因为近远侄子节点为红色时，不为父节点的颜色
                 deleteNode = root;
             }
         } else {
             // 删除节点为父节点的右子节点
             // 获取兄弟节点
             Node s = leftOf(parentOf(deleteNode));
             if (colorOf(s) == Node.RED) {
                 // 兄弟节点为红色，父结点与兄弟节点颜色互换，然后父结点右旋
                 setColor(s, Node.BLACK);
                 setColor(parentOf(deleteNode), Node.RED);
                 rotateRight(deleteNode.parent);
                 // 记录新的兄弟节点
                 s = leftOf(parentOf(deleteNode));
             }

             // 到达这里代表兄弟节点为黑色
             if (colorOf(leftOf(s)) == Node.BLACK && colorOf(rightOf(s)) == Node.BLACK) {
                 // 删除节点的两个子节点均为黑色，将兄弟节点设置为红色
                 setColor(s, Node.RED);
                 deleteNode = parentOf(deleteNode);
             } else {
                 if (colorOf(rightOf(s)) == Node.RED) {
                     // 近侄子节点为红色，兄弟节点与近侄子节点颜色互换，然后兄弟节点左旋，变成远侄子节点为红色情况
                     setColor(s, Node.RED);
                     setColor(rightOf(s), Node.BLACK);
                     rotateLeft(s);
                     // 记录新的兄弟节点
                     s = leftOf(parentOf(deleteNode));
                 }
                 // 到达这里为远侄子节点为红色情况
                 // 父节点与兄弟节点颜色互换，然后远侄子节点变为红色，父节点右旋
                 setColor(s, colorOf(parentOf(deleteNode)));
                 setColor(parentOf(deleteNode), Node.BLACK);
                 setColor(leftOf(s), Node.BLACK);
                 rotateRight(deleteNode.parent);
                 // 树已经平衡，这里等于root是为了保证root的颜色，因为近远侄子节点为红色时，不为父节点的颜色
                 deleteNode = root;
             }
         }
     }
     deleteNode.color = Node.BLACK;
 }

 // 找出删除节点的替代节点
 private Node successor(Node d) {
     if (d == null) {
         return null;
     } else if (d.right != null) {
         // 删除节点存在右子节点,找出右子树中最左侧节点(最小值)代替
         Node p = d.right;
         while (p.left != null)
             p = p.left;
         return p;
     } else {
         // 删除节点只有左子节点,找出左子树中最右侧节点(最大值)代替
         Node p = d.parent;
         Node ch = d;
         while (p != null && ch == p.right) {
             ch = p;
             p = p.parent;
         }
         return p;
     }
 }

红黑树遍历

		// 前序遍历
		public void preOrder(Node node) {
			if (node != null) {
				// 根节点
				System.out.print(node.data + " ");
				// 左子树遍历
				preOrder(node.left);
				// 右子树遍历
				preOrder(node.right);
			}
		}
	
		// 中序遍历
		public void infixOrder(Node node) {
			if (node != null) {
				// 左子树遍历
				infixOrder(node.left);
				// 根节点
				System.out.print(node.data + " ");
				// 右子树遍历
				infixOrder(node.right);
			}
		}
	
		// 后序遍历
		public void postOrder(Node node) {
			if (node != null) {
				// 左子树遍历
				postOrder(node.left);
				// 右子树遍历
				postOrder(node.right);
				// 根节点
				System.out.print(node.data + " ");
			}
		}

测试

测试代码如下：

	package com.xxliao.datastructure.tree.read_black_tree;

import java.util.TreeMap;

/**
 * @author xxliao
 * @description: 红黑树 测试客户端
 * @date 2024/5/29 0:44
 */

public class RedBlackTreeTestClient {

    public static void main(String[] args) {
        // 创建树
        RedBlackTree avlTree = new RedBlackTree();
        // 数据源,无序的1~10
        int[] array = { 4, 6, 1, 3, 2, 7, 8, 9, 5, 10 };
        // 添加数据
        for (int i = 0; i < array.length; i++) {
            avlTree.put(array[i]);
        }
        // 前序遍历
        System.out.print("前序遍历");
        avlTree.preOrder(avlTree.getRoot());
        System.out.println();
        // 中序遍历
        System.out.print("中序遍历");
        avlTree.infixOrder(avlTree.getRoot());
        System.out.println();
        // 后序遍历
        System.out.print("后序遍历");
        avlTree.postOrder(avlTree.getRoot());
        System.out.println();
        // 删除5
        System.out.println("删除5");
        avlTree.remove(5);
        // 前序遍历
        System.out.print("前序遍历");
        avlTree.preOrder(avlTree.getRoot());
        System.out.println();
        // 中序遍历
        System.out.print("中序遍历");
        avlTree.infixOrder(avlTree.getRoot());
        System.out.println();
        // 后序遍历
        System.out.print("后序遍历");
        avlTree.postOrder(avlTree.getRoot());
        System.out.println();
    }
}

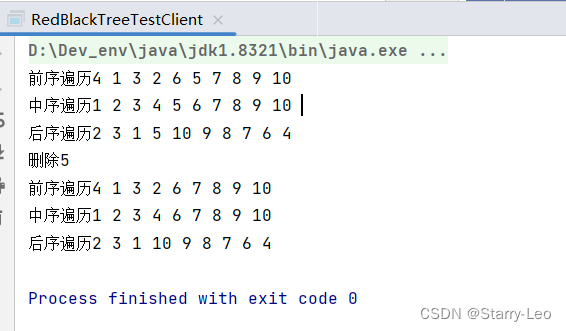
测试结果：
在这里插入图片描述