曲线插值法
进行路径的曲线拟合,常见的曲线插值有:
| 多项式曲线 | 双圆弧段曲线 | 贝塞尔曲线 |
| B样条曲线 | 正弦函数曲线 |
核心思想:基于预先构造的曲线类型,根据车辆期望达到的状态
(比如:要求车辆达到某点的速度和加速度为期望值),将此期望值作为边界条件带入曲线类型进行方程式求解
| 项数 | 期望点维度 |
|---|---|
| 三次多项式 | 位置和速度 |
| 五次多项式 | 位置、速度、加速度 |
| 七次多项式 | 位置、速度、加速度、加加速度(冲击度) |
下述是三、五、七次多项式曲线的公式 以及 在模拟环境下的示意


小车图MATLAB代码
clc
clear
close all
d=3.5;
len_line=30;
W=1.75;
L=4.7;
x1=20;
t0=0;
t1=3;
state_t0=[0,-d/2;5,0;0,0];
state_t1=[20,d/2;5,0;0,0];
x2=state_t0(1);
%%画场景示意图
figure(1)
%画灰色路面图
GreyZone=[-5,-d-0.5;-5,d+0.5;len_line,d+0.5;len_line,-d-0.5];
fill(GreyZone(:,1),GreyZone(:,2),[0.5 0.5 0.5]);
hold on
%画小车
fill([x1,x1,x1+L,x1+L],[-d/2-W/2,-d/2+W/2,-d/2+W/2,-d/2-W/2],'b')
fill([x2,x2,x2-L,x2-L],[-d/2-W/2,-d/2+W/2,-d/2+W/2,-d/2-W/2],'y')
%分界线
plot([-5,len_line],[0,0],'w--','LineWidth',2);%分界线
plot([-5,len_line],[d,d],'w','LineWidth',2);%左边界线
plot([-5,len_line],[-d,-d],'w','LineWidth',2);%右边界线
%设置坐标轴显示图
axis equal
set(gca,'XLim',[-5 len_line]);
set(gca,'YLim',[-4 4]);
%%五次多项式轨迹生成
%计算A和B两个系数矩阵
X=[state_t0(:,1);state_t1(:,1)];
Y=[state_t0(:,2);state_t1(:,2)];
T=[t0^5 t0^4 t0^3 t0^2 t0 1;
5*t0^4 4*t0^3 3*t0^2 2*t0 1 0;
20*t0^3 12*t0^2 6*t0 1 0 0;
t1^5 t1^4 t1^3 t1^2 t1 1;
5*t1^4 4*t1^3 3*t1^2 2*t1 1 0;
20*t1^3 12*t1^2 6*t1 1 0 0];
A= T \ X;
B= T \ Y;
%将实践从t0到t1离散化,获得离散时刻的轨迹坐标
t=(t0:0.05:t1)';
path=zeros(length(t),4);
for i=1:length(t)
%纵向位置坐标
path(i,1)=[t(i)^5,t(i)^4,t(i)^3,t(i)^2,t(i),1]*A;
%横向位置坐标
path(i,2)=[t(i)^5,t(i)^4,t(i)^3,t(i)^2,t(i),1]*B;
%纵向速度
path(i,3)=[5*t(i)^4,4*t(i)^3,3*t(i)^2,2*t(i),1,0]*A;
end
%画换道轨迹
plot(path(:,1),path(:,2),'r--','LineWidth',1.5);
%%分析速度
%横向速度
figure
plot(t,path(:,4),'k');
xlabel('时间/s');
ylabel('横向速度/m/s');
%纵向速度
figure
plot(t,path(:,3),'k');
xlabel('时间/s');
ylabel('纵向速度/m/s');
人工势场法
基本思想:在障碍物周围构建障碍物斥力势场,在目标点周围构建引力势场

引力势场主要与汽车和目标点间的距离有关,
距离越大,汽车所受的势能值就越大:
距离越小,汽车所受的势能值则越小,
引力势场的函数:

决定障碍物斥力势场的因素是汽车与障碍物间的距离,当汽车未进入障碍物的影响范围时,其受到的势能值为零
在汽车进入障碍物的影响范围后
两者之间的距离越大,汽车受到的势能值就越小
距离越小,汽车受到的势能值就越大
斥力势场的势场函数为:

其中k为正比例系数,p(g,9)为一矢量,方向为从障碍物指向汽车,大小为汽车与障碍物问的距离
![]()
为一常数,表示障碍物对汽车产生作用的最大距离
相应的斥力为斥力场的负梯度:

存在问题
- 目标不可到达,障碍物和目标点距离太近:引力为0时,斥力不为0,所以无法“停车”
- 陷入局部最优问题:车辆在某个位置时,如果若干个障碍无得合斥力与目标点的引力大小相等,方向相反,则合力为0,无法向前搜索避障路径。
改进1:改进障碍物斥力势场函数来解决以上两个问题

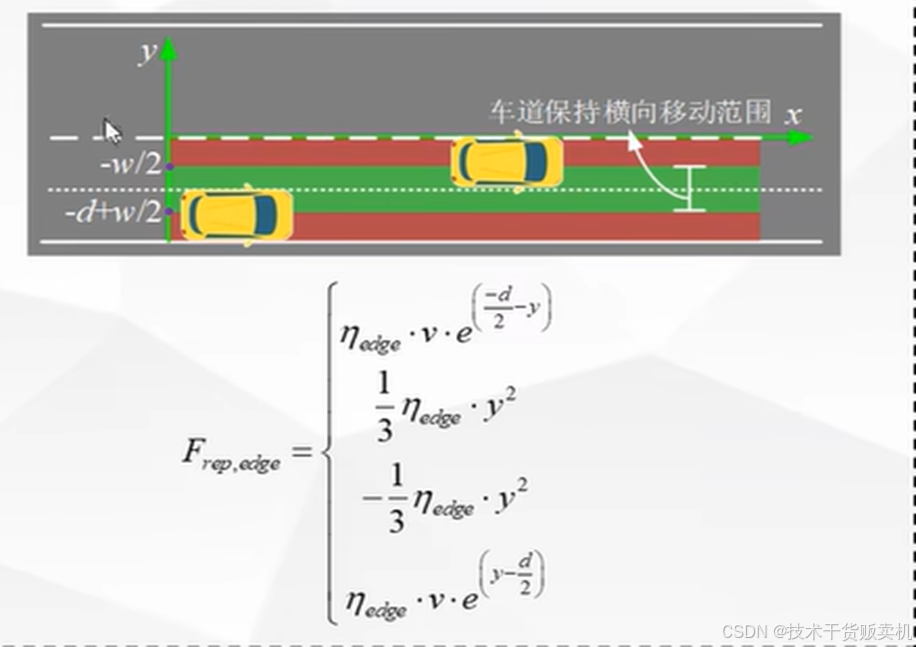
改进2:建立道路边界斥力势场,以限制汽车的行驶区域
























 1352
1352

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








