1.给定一个区间的集合,找到需要移除区间的最小数量,使剩余区间互不重叠。
注意: 可以认为区间的终点总是大于它的起点。 区间 [1,2] 和 [2,3] 的边界相互“接触”,但没有相互重叠。
#include <bits/stdc++.h>
using namespace std;
bool cmp(const vector<int>&a,const vector<int>&b)
{
return a[0]<b[0];
}
int find(vector<vector<int>>& num)
{
if(num.size()==0)
return 0;
sort(num.begin(),num.end(),cmp);
int count=0;
for(int i=1;i<num.size();i++)
{
if(num[i][0]<num[i-1][1])
{
count++;
num[i][1]=min(num[i-1][1],num[i][1]);
}
}
return count;
}
int main()
{
vector<vector<int>> num={{1,2},{3,6},{7,12},{4,8},{10,16}};
int t=find(num);
cout<<t;
return 0;
}
思路:首先我们要进行排序,按照右边界排序,从左向右记录非交叉区间的个数。最后用区间总数减去非交叉区间的个数就是需要移除的区间个数了。
此时问题就是要求非交叉区间的最大个数。
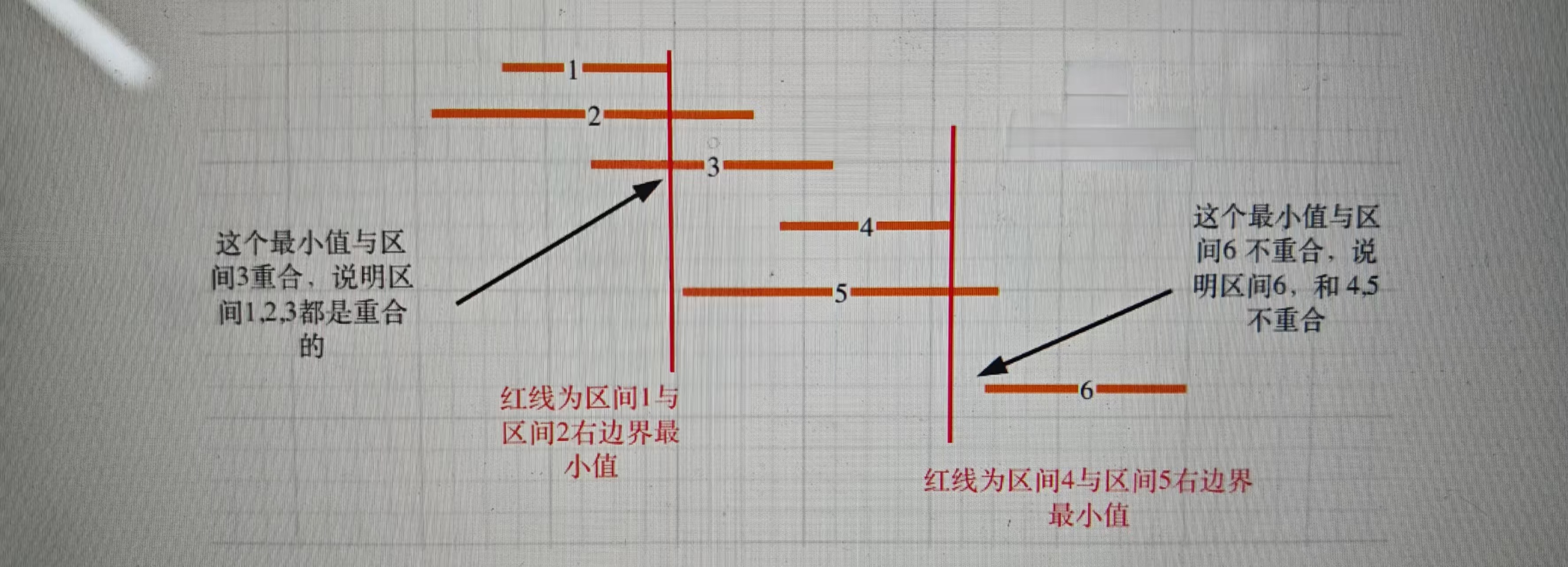
区间,1,2,3,4,5,6都按照右边界排好序。
当确定区间 1 和 区间2 重叠后,如何确定是否与 区间3 也重贴呢?
就是取 区间1 和 区间2 右边界的最小值,因为这个最小值之前的部分一定是 区间1 和区间2 的重合部分,如果这个最小值也触达到区间3,那么说明 区间 1,2,3都是重合的。接下来就是找大于区间1结束位置的区间,是从区间4开始。
区间4结束之后,再找到区间6,所以一共记录非交叉区间的个数是三个。
总共区间个数为6,减去非交叉区间的个数3。移除区间的最小数量就是3。
2.字符串 S 由小写字母组成。我们要把这个字符串划分为尽可能多的片段,同一字母最多出现在一个片段中。返回一个表示每个字符串片段的长度的列表。
#include <bits/stdc++.h>
using namespace std;
vector<int> find(string s)
{
int hash[27]={0};
for(int i=0;i<s.size();i++)
{
hash[s[i]-'a']=i;
}
int left=0;
int right=0;
vector<int> result;
for(int i=0;i<s.size();i++)
{
right=max(hash[s[i]-'a'],right);
if(i==right)
{
result.push_back(right-left+1);
left=i+1;
}
}
return result;
}
int main()
{
string s="ababcbacadefegdehijhklij";
vector<int> result=find(s);
for(int n:result)
{
cout<<n<<" ";
}
return 0;
}
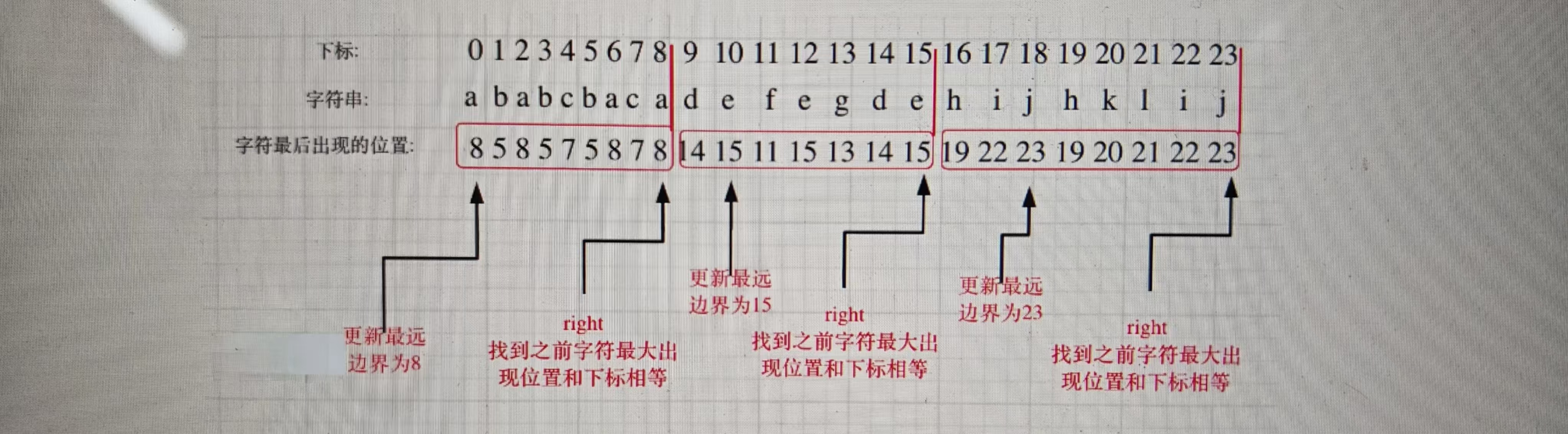
思路:这道题在遍历的过程中相当于是要找每一个字母的边界,如果找到之前遍历过的所有字母的最远边界,说明这个边界就是分割点了。此时前面出现过所有字母,最远也就到这个边界了。
可以分为如下两步:
1.统计每一个字符最后出现的位置。
2.从头遍历字符,并更新字符的最远出现下标,如果找到字符最远出现位置下标和当前下标相等了,则找到了分割点。
3.给出一个区间的集合,请合并所有重叠的区间。
#include <bits/stdc++.h>
using namespace std;
bool cmp(const vector<int>& a,const vector<int>& b)
{
return a[0]<b[0];
}
vector<vector<int>> find(vector<vector<int>>& num)
{
vector<vector<int>> result;
if(num.size()==0)
return result;
sort(num.begin(),num.end(),cmp);
result.push_back(num[0]);
for(int i=1;i<num.size();i++)
{
if(num[i][0]<=num[i-1][1])
{
result.back()[1]=max(num[i][1],result.back()[1]);
}
else{
result.push_back(num[i]);
}
}
return result;
}
int main()
{
vector<vector<int>> num={{1,3},{8,10},{2,6},{15,18}};
vector<vector<int>> t=find(num);
for(const auto& n:t)
{
for(int m:n)
{
cout<<m<<" ";
}
cout<<endl;
}
return 0;
}
思路:本题的本质是判断重叠区间问题。先排序,让所有的相邻区间尽可能的重叠在一起,按左边界,或者右边界排序都可以,处理逻辑稍有不同。按照左边界从小到大排序之后,如果 intervals[i][0] <= intervals[i - 1][1] 即intervals[i]的左边界 <= intervals[i - 1]的右边界,则一定有重叠。(本题相邻区间也算重贴,所以是<=)。
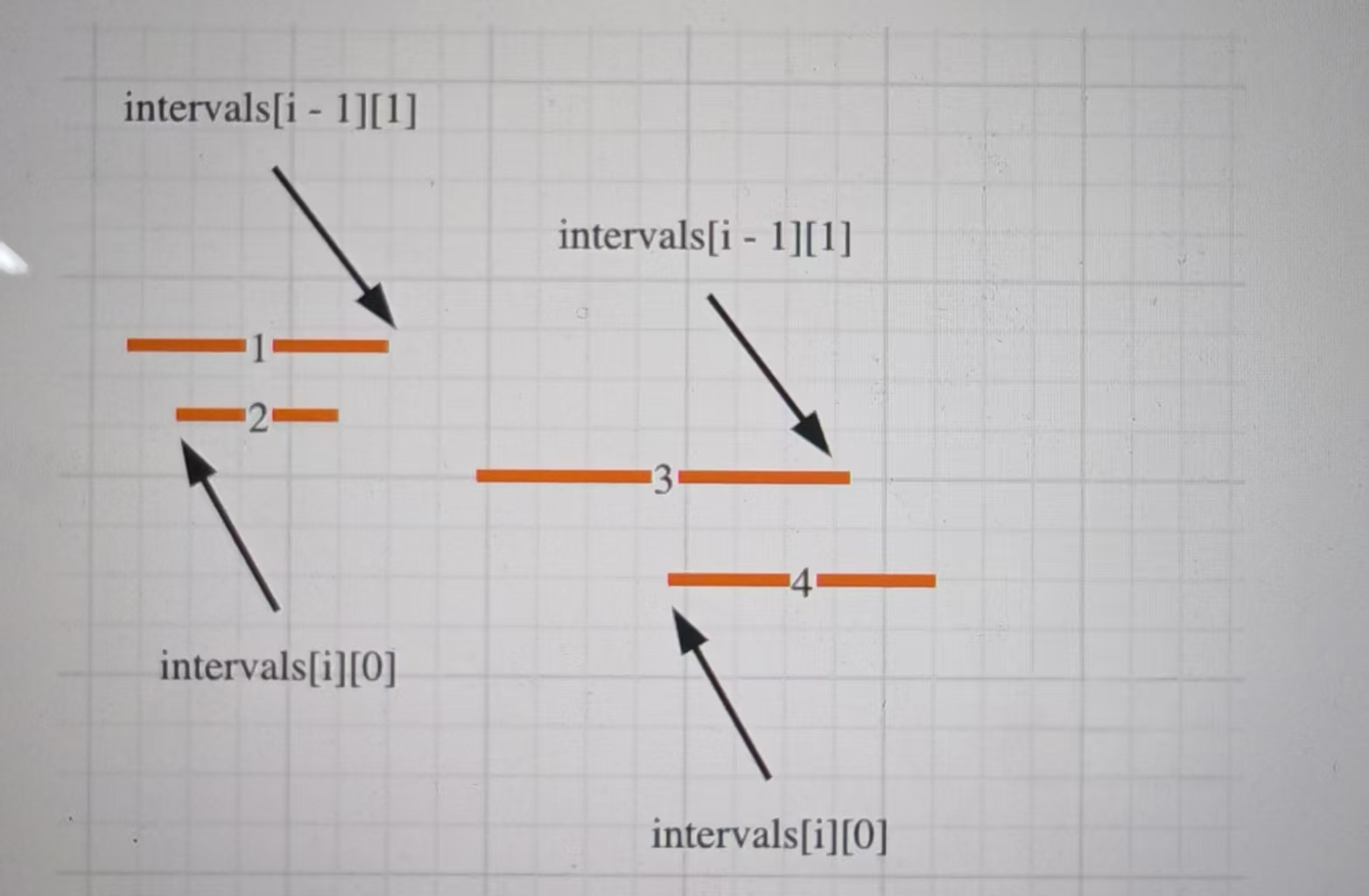
知道如何判断重复之后,剩下的就是合并了,如何去模拟合并区间呢?
其实就是用合并区间后左边界和右边界,作为一个新的区间,加入到result数组里就可以了。如果没有合并就把原区间加入到result数组。























 488
488

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








