加油站分发糖果

最新推荐文章于 2025-05-30 23:54:13 发布

默默修炼的小趴菜

最新推荐文章于 2025-05-30 23:54:13 发布

阅读量1.2k

点赞数 33

文章标签：算法

本文链接：https://blog.youkuaiyun.com/2301_82195117/article/details/146699545

版权

1.在一条环路上有 N 个加油站，其中第 i 个加油站有汽油 gas[i] 升。

你有一辆油箱容量无限的的汽车，从第 i 个加油站开往第 i+1 个加油站需要消耗汽油 cost[i] 升。你从其中的一个加油站出发，开始时油箱为空。

如果你可以绕环路行驶一周，则返回出发时加油站的编号，否则返回 -1

#include <bits/stdc++.h>
using namespace std;
int find(vector<int>& gas,vector<int>& cos)
{
   int curSum=0;
   int totalSum=0;
   int start=0;
   for(int i=0;i<gas.size();i++)
   {
       curSum+=(gas[i]-cos[i]);
       totalSum+=(gas[i]-cos[i]);
       if(curSum<0)
       {
           start=i+1;
           curSum=0;
       }
   }
   if(totalSum<0)
   return -1;
   return start;

}
int main()
{
   vector<int> gas={1,2,3,4,5};
   vector<int> cos={3,4,5,1,2};
   int t=find(gas,cos);
   cout<<t;
   return 0;
}
思路：首先如果总油量减去总消耗大于等于零那么一定可以跑完一圈，说明各个站点的加油站剩油量rest[i]相加一定是大于等于零的。每个加油站的剩余量rest[i]为gas[i] - cost[i]。

i从0开始累加rest[i]，和记为curSum，一旦curSum小于零，说明[0, i]区间都不能作为起始位置，因为这个区间选择任何一个位置作为起点，到i这里都会断油，那么起始位置从i+1算起，再从0计算curSum。

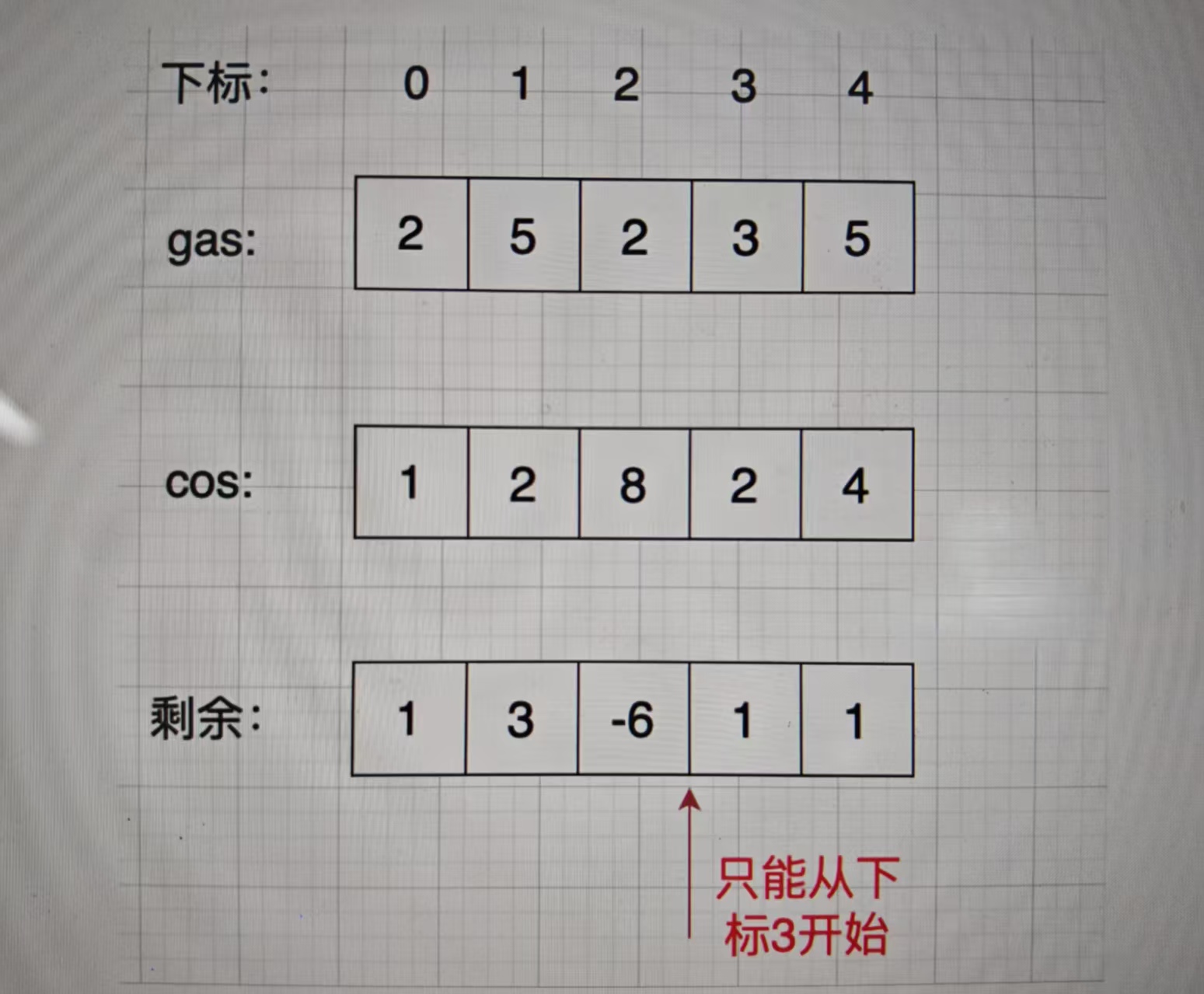
那么为什么一旦[0，i] 区间和为负数，起始位置就可以是i+1呢，i+1后面就不会出现更大的负数？

如果出现更大的负数，就是更新i，那么起始位置又变成新的i+1了。

那有没有可能 [0，i] 区间选某一个作为起点，累加到 i这里 curSum是不会小于零呢？

如果 curSum<0 说明区间和1 + 区间和2 < 0，那么假设从上图中的位置开始计数curSum不会小于0的话，就是区间和2>0。

区间和1 + 区间和2 < 0 同时区间和2>0，只能说明区间和1 < 0，那么就会从假设的箭头初就开始从新选择起始位置了。

那么局部最优：当前累加rest[i]的和curSum一旦小于0，起始位置至少要是i+1，因为从i之前开始一定不行。全局最优：找到可以跑一圈的起始位置。

2.老师想给孩子们分发糖果，有 N 个孩子站成了一条直线，老师会根据每个孩子的表现，预先给他们评分。

你需要按照以下要求，帮助老师给这些孩子分发糖果：

每个孩子至少分配到 1 个糖果。

相邻的孩子中，评分高的孩子必须获得更多的糖果。

那么这样下来，老师至少需要准备多少颗糖果呢？

#include <bits/stdc++.h>
using namespace std;
int find(vector<int>& num)
{
   vector<int> candy(num.size(),1);
   for(int i=1;i<num.size();i++)
   {
       if(num[i]>num[i-1])
       {
           candy[i]=candy[i-1]+1;
       }
   }
   for(int i=num.size()-2;i>=0;i--)
   {
       if(num[i]>num[i+1])
       {
           candy[i]=max(candy[i+1]+1,candy[i]);
       }
   }
   int result=0;
   for(int i=0;i<candy.size();i++)
   {
   result+=candy[i];
   }
   return result;
}
int main()
{
   vector<int> num={1,2,2,5,4,3,2};
   int t=find(num);
   cout<<t;
   return 0;
}