子集|| 递增子序列 全排列

1.给定一个可能包含重复元素的整数数组 nums，返回该数组所有可能的子集（幂集）。

说明：解集不能包含重复的子集。

示例:

输入: [1,2,2]

输出: [ [2], [1], [1,2,2], [2,2], [1,2], [] ]

#include <bits/stdc++.h>
using namespace std;
vector<vector<int>> result;
vector<int> path;
void backtracking(vector<int>& num,int startIndex,vector<bool>& used)
{
    result.push_back(path);
    for(int i=startIndex;i<num.size();i++)
    {
        if(i>0&&num[i]==num[i-1]&&used[i-1]==false)
        continue;
        path.push_back(num[i]);
        used[i]=true;
        backtracking(num,i+1,used);
        path.pop_back();
        used[i]=false;
    }
    
 } 
vector<vector<int>> combine(vector<int>& num)
{
    result.clear();
    path.clear();
    vector<bool> used(num.size(),false);
    sort(num.begin(),num.end());
    backtracking(num,0,used);
    return result;
}
int main()
{
    vector<int> num={1,2,2};
    vector<vector<int>> t=combine(num);
    for(const auto& m:t)
    {
        for(int n:m)
        {
            cout<<n<<" ";
        }
        cout<<endl;
    }
    return 0;
}
 

思路：这道题主要难点在于求取的子集要去重，用示例中的[1, 2, 2] 来举例，如图所示： （注意去重需要先对集合排序）

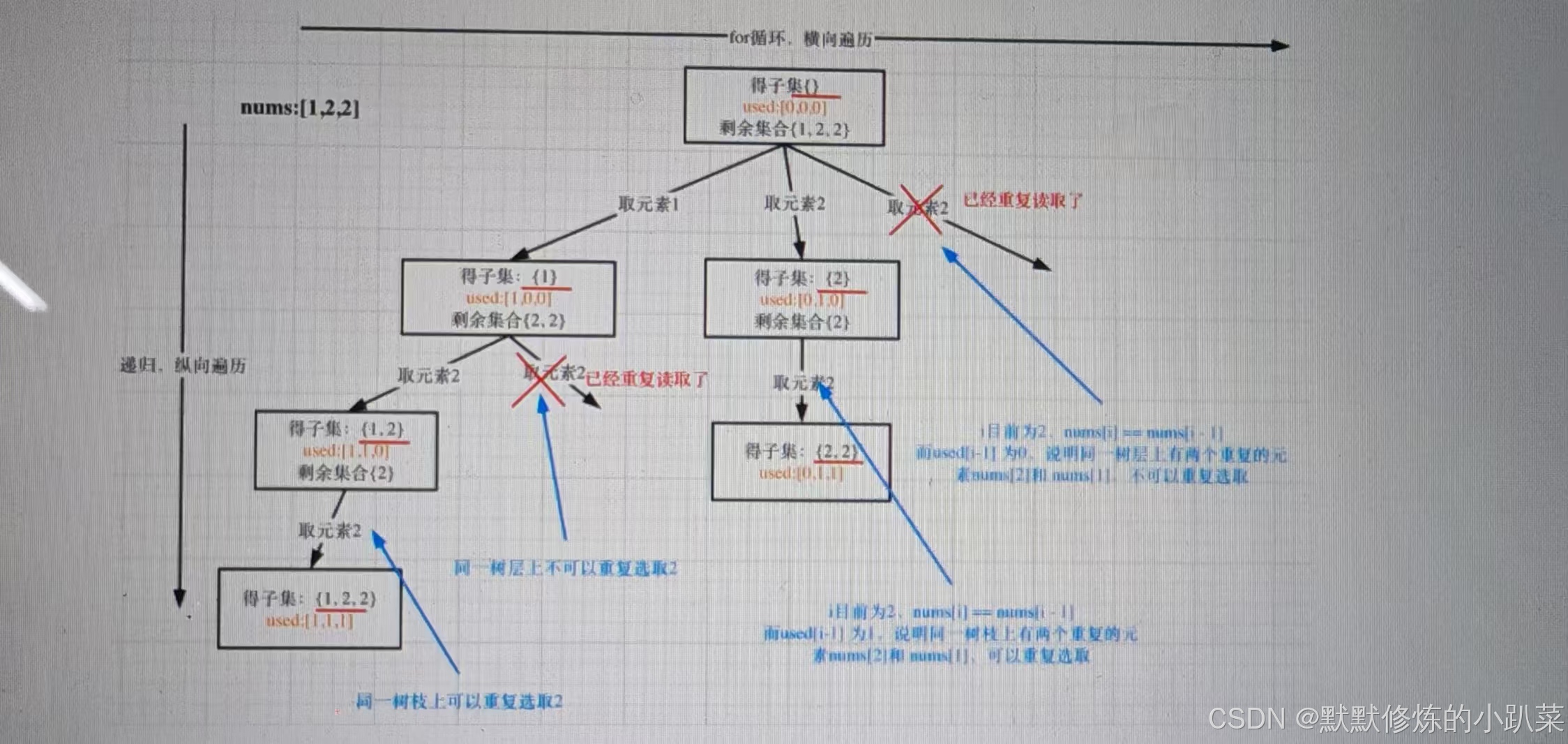
从图中可以看出，同一树层上重复取2 就要过滤掉，同一树枝上就可以重复取2，因为同一树枝上元素的集合才是唯一子集！

2.给定一个整型数组, 你的任务是找到所有该数组的递增子序列，递增子序列的长度至少是2。

示例:

输入: [4, 6, 7, 7]

输出: [[4, 6], [4, 7], [4, 6, 7], [4, 6, 7, 7], [6, 7], [6, 7, 7], [7,7], [4,7,7]]

说明:

给定数组的长度不会超过15。

数组中的整数范围是 [-100,100]。

给定数组中可能包含重复数字，相等的数字应该被视为递增的一种情况。

#include <bits/stdc++.h>
using namespace std;
vector<vector<int>> result;
vector<int> path;
void backtracking(vector<int>& num,int startIndex)
{
    if(path.size()>1)
    result.push_back(path);
    unordered_set<int> uset;
    for(int i=startIndex;i<num.size();i++)
    {
        if((!path.empty()&&num[i]<path.back())||uset.find(num[i])!=uset.end())
        continue;
        uset.insert(num[i]);
        path.push_back(num[i]);
        backtracking(num,i+1);
        path.pop_back();
     } 
}
vector<vector<int>> combine(vector<int>& num)
{
    result.clear();
    path.clear();
    backtracking(num,0);
    return result;
}
int main()
{
    vector<int> num={4,7,6,7};
    vector<vector<int>> t=combine(num);
    for(const auto& m:t)
    {
        for(int n:m)
        {
            cout<<n<<" ";
        }
        cout<<endl;
    }
    return 0;
}

思路：先用[4, 7, 6, 7]这个数组来举例，抽象为树形结构如图：

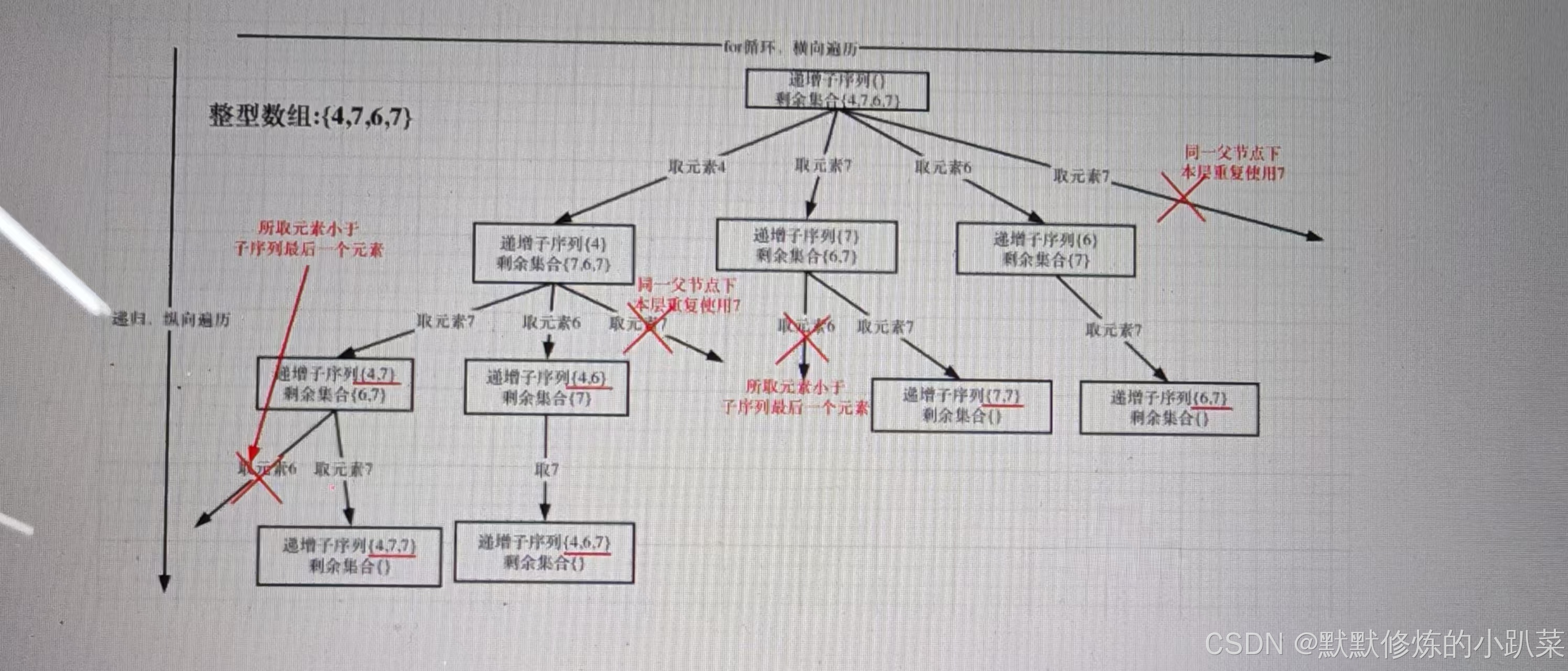
本题求子序列，很明显一个元素不能重复使用，所以需要startIndex，调整下一层递归的起始位置。本题其实类似求子集问题，也是要遍历树形结构找每一个节点，可以不加终止条件，startIndex每次都会加1，并不会无限递归。本题收集结果有所不同，题目要求递增子序列大小至少为2。在图中可以看出，同一父节点下的同层上使用过的元素就不能再使用了。unordered_set<int> uset; 是记录本层元素是否重复使用，新的一层uset都会重新定义（清空），所以要知道uset只负责本层！

3给定一个 没有重复 数字的序列，返回其所有可能的全排列。

示例:

输入: [1,2,3]

输出: [ [1,2,3], [1,3,2], [2,1,3], [2,3,1], [3,1,2], [3,2,1] ]

#include <bits/stdc++.h>
using namespace std;
vector<vector<int>> result;
vector<int> path;
void backtracking(vector<int>& num,vector<bool>& used)
{
    if(path.size()==num.size())
    {
        result.push_back(path);
        return ;
    }
    for(int i=0;i<num.size();i++)
    {
        if(used[i]==true)
        continue;
        used[i]=true;
        path.push_back(num[i]);
        backtracking(num,used);
        used[i]=false;
        path.pop_back();        
        
    }
    
 } 
vector<vector<int>> combine(vector<int>& num)
{
    result.clear();
    path.clear();
    vector<bool> used(num.size(),false);
    backtracking(num,used);
    return result;
}
int main()
{
    vector<int> num={1,2,3};
    vector<vector<int>> t=combine(num);
    for(const auto& m:t)
    {
        for(int n:m)
        {
            cout<<n<<" ";
        }
        cout<<endl;
    }
    return 0;
}
 

思路：先以[1,2,3]为例，抽象成树形结构如下：

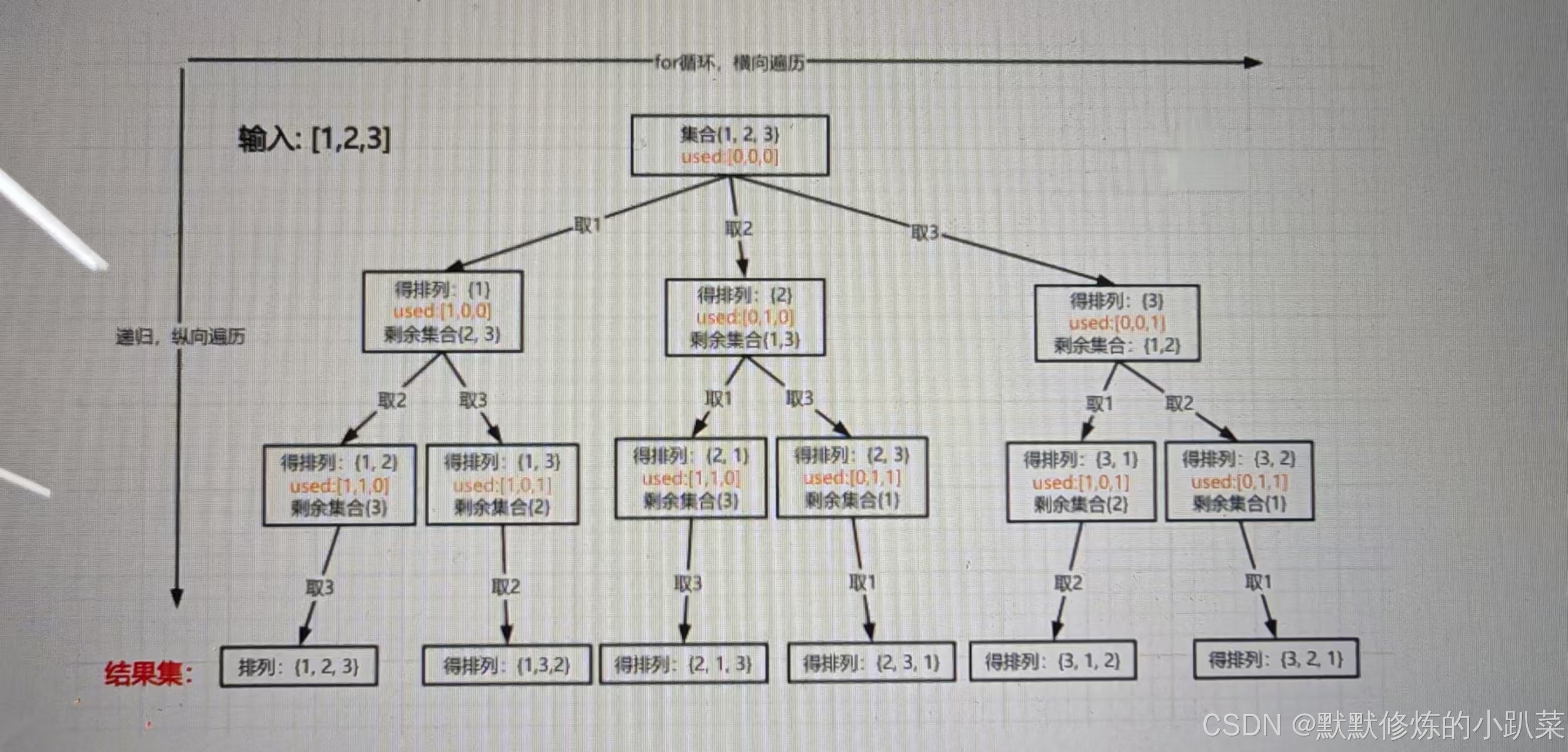
首先排列是有序的，也就是说 [1,2] 和 [2,1] 是两个集合，这和之前分析的子集以及组合所不同的地方，可以看出元素1在[1,2]中已经使用过了，但是在[2,1]中还要在使用一次1，所以处理排列问题就不用使用startIndex了。但排列问题需要一个used数组，标记已经选择的元素。

可以看出叶子节点，就是收割结果的地方。当收集元素的数组path的大小达到和nums数组一样大的时候，说明找到了一个全排列，也表示到达了叶子节点。

used数组，其实就是记录此时path里都有哪些元素使用了，一个排列里一个元素只能使用一次