一.基于用户的协同过滤算法(UserCF)
1.基本原理
UserCF基于用户行为数据,找到与目标用户兴趣相似的用户群体,然后将这些相似用户喜欢的物品推荐给目标用户。核心是计算用户之间的相似度,即相似性度量方法。
2.相似性度量方法
杰卡德(Jaccard)相似系数

值在0到1之间,越接近1表示两个集合越相似,0表示无相似元素。常用于文本分类、计算用户购物相似度等。
余弦相似度
从向量的角度进行描述,令矩阵 A 为用户-物品交互矩阵,矩阵的行表示用户,列表示物品。
设用户和物品数量分别为 m,n,交互矩阵A就是一个 m 行 n 列的矩阵。
矩阵中的元素均为 0/1。若用户 i对物品 j存在交互,那么 Ai,j=1,否则为 0 。
那么,用户之间的相似度可以表示为:向量u 点乘 向量v的积 除以 向量u和向量v的绝对值
下面是展示结果

根据公式可算出
符合用户i和用户j之间的余弦相似度
皮尔逊相关系数
皮尔逊相关系数与余弦相似度的计算公式非常的类似

根据计算公式

满足结果
3.计算相似度
计算 Alice 与其他用户的余弦相似度,用户向量Alice(5,3,4,4) user1(3,1,2,3) user2(4,3,4,3) user3(3,3,1,5) user4(1,5,5,2)

sim(Alice,user1) = 0.975,sim(Alice,user2) = 0.992,sim(Alice,user3) = 0.890,sim(Alice,user4) = 0.796
显而易见,根据余弦相似度,相似度最高的是user2,其次是user1。根据相似度用户计算 Alice对物品5的最终得分,用户1对物品5的评分是3,用户2对物品5的打分是5, 那么根据上面的计算公式, 可以计算出 Alice 对物品5的最终得分是4.87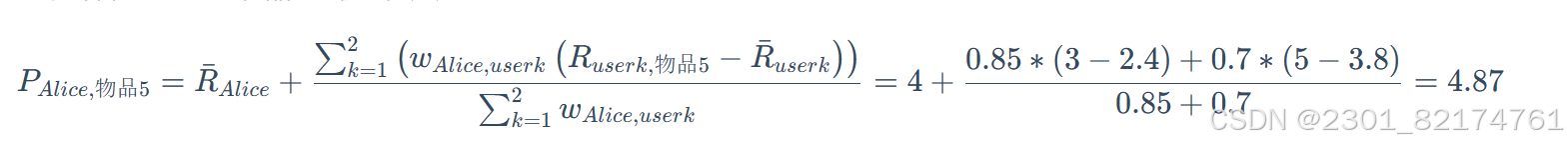
可知对Alice来说物品1和物品5更有推荐性。
二.基于物品的协同过滤算法(ItemCF)
1.基本原理
首先计算物品之间的相似度,通常通过共同被用户喜欢的情况来衡量。然后,对于一个目标用户,根据其历史行为中喜欢的物品,找出与之相似的其他物品并推荐给该用户。
2.计算相似度

物品1(3,4,3,1) 物品2(1,3,3,5) 物品3(2,4,1,5) 物品4(3,3,5,2) 物品5(3,5,4,1)
sim(物品1,物品5) = 0.994
sim(物品2,物品5)= 0.738
sim(物品3,物品5)= 0.722
sim(物品4,物品5)= 0.939
可知与物品5最相似的2个物品是 item1 和 item4


由上面公式算出最终得分为4.6分
3.协调过滤算法的问题分析
泛化能力弱
即协同过滤无法将两个物品相似的信息推广到其他物品的相似性上。
导致的问题是热门物品具有很强的头部效应, 容易跟大量物品产生相似, 而尾部物品由于特征向量稀疏, 导致很少被推荐。
冷启动问题
新用户或新物品缺乏交互数据,无法有效计算相似性,影响推荐质量。
难以适应动态数据
传统方法需要批量更新模型
4.协同过滤算法的改进
矩阵分解降低维度,混合推荐系统改善冷启动,增量学习支持实时更新
三.矩阵分解
1.隐语义模型
它的核心思想是从数据出发,进行个性化推荐是用户和物品之间隐含的联系,将用户和物品通过中介隐含因子联系起来。
2.矩阵分解算法
计算原理
通过分解协同过滤的共现矩阵(评分矩阵)来得到用户和物品的隐向量

k是隐向量维度, 也就是隐含特征个数,一般而言, k越大隐向量能承载的信息内容越多,表达能力也会更强,但相应的学习难度也会增加.
Funk-SVD算法
Funk-SVD的思想很简单:把求解上面两个矩阵的参数问题转换成一个最优化问题, 可以通过训练集里面的观察值利用最小化来学习用户矩阵和物品矩阵。

向量 表示用户 u 的隐向量,向量
表示物品 i的隐向量。
用户和物品的向量内积 , 作为用户对物品的预测评分

为方便后续求解,给 SSE 增加系数 1/2

模型预测越准确等价于预测误差越小,那么优化的目标函数变为

为了控制模型的复杂度。在原有模型的基础上加入l2正则化来防止过拟合。

BiassSVD算法
在FunkSVD的基础上,增加了全局平均偏差、用户偏差和物品偏差,模型复杂度相对较高,能够更细致地捕捉数据中的各种偏差因素对评分的影响。

μ: 该参数反映的是推荐模型整体的平均评分,一般使用所有样本评分的均值。
:用户偏差系数。可以使用用户 uu 给出的所有评分的均值, 也可以当做训练参数。
:物品偏差系数。可以使用物品 ii 收到的所有评分的均值, 也可以当做训练参数。
在加入正则项的FunkSVD的基础上,BiasSVD 的目标函数如下:
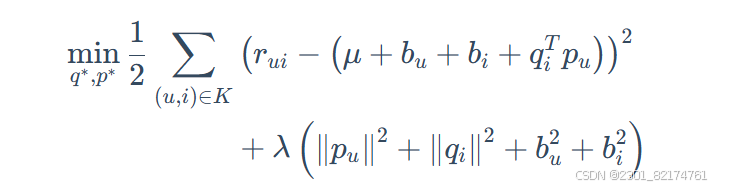
























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








