目录
一、PPPH软件论文
PPPH:一款基于MATLAB的多GNSS精密单点定位分析软件
1、摘要
不同GNSS星座的融合为提高精密单点定位( precise point positioning,PPP )性能提供了巨大的机遇。考虑到利用多星座和多频GNSS的潜在优势的备选方案数量有限,我们开发了基于MATLAB的GNSS分析软件,命名为PPPH。PPPH能够处理GPS、GLONASS、Galileo和BeiDou数据,并根据用户的偏好形成它们的不同组合。得益于其友好的图形界面,PPPH允许用户确定各种处理选项和参数。PPPH除了包括每个历元的估计参数的输出文件外,还提供了一些用于评估结果的分析和绘图工具,如定位误差、对流层天顶总延迟、接收机钟差估计、卫星数、Dilution of Precision (DOP)等。另一方面,我们进行了实验测试,既验证了PPPH的性能,又评估了多GNSS对PPP的潜在好处。结果表明,PPPH提供了可与通用标准相媲美的PPP解决方案,并有助于提高多GNSS融合的PPP性能。因此,我们介绍了一个简单易用、性能稳定、具有模块化结构和开放性的GNSS分析软件。
Keywords:Precise point positioning (PPP) · Multi-GNSS · MATLAB software · PPPH
2、引言
精密单点定位(PPP)是一种在全球范围内仅使用一个接收器即可实现厘米或分米级定位精度的技术(Zumberge等人,1997年;Kouba和Héroux 2001年)。在过去十年中,PPP由于其独特的优点,如操作简单、成本效益高、消除了对基站的要求,在GNSS(全球导航卫星系统)界引起了相当大的关注。PPP已被广泛应用于许多对定位精度要求较高的GNSS应用中。虽然PPP能够满足大多数GNSS应用对定位精度的要求,但要达到特定的定位精度还需要相当长的观测周期。这段时间通常称为收敛时间,通常需要50分钟才能达到10 cm或更高的水平精度(Choy等人,2017年)。相对较长的收敛时间仍然是PPP的主要缺点,这限制了PPP的广泛应用。除了用户环境和接收机的地理位置外,收敛时间达到特定精度水平主要取决于可见卫星的数量和几何形状。近年来,GLONASS全轨道星座的恢复以及Galileo、BeiDou ( BDS )等新卫星系统的出现,为PPP提供了额外的频率和卫星资源。因此,不同GNSS星座的组合,即多GNSS,加强了可见卫星的数量和几何形状,因此,在定位精度和收敛时间( Cai和Gao 2013 ;伊格尔特等, 2014 ; Togedor et al 2014 ; Cai et al . 2015)方面提供了改善PPP性能的机会。
随着全球导航卫星系统PPP在定位导航应用中的重要性,对能够进行多个全球导航卫星系统PPP分析的GNSS分析软件的需求也在不断增加。然而,与仅包含GPS观测的传统PPP方法相比,多GNSS观测组合需要更复杂的模型和算法。因此,多模GNSS PPP处理需要更先进的软件解决方案来利用新的卫星和频率。GNSS用户经常使用的GNSS数据处理软件包有瑞士伯尔尼大学研发的精密定位与定轨软件Bernese、GAMIT / GLOBK、GIPSY / OASIS等,虽然这些软件包本质上并不是专门用于精密单点定位,但它们仍然提供了PPP解决方案以及其他功能。然而,由于其复杂的结构和综合的处理功能,对于一个正在寻求PPP分析的标准用户来说,它们可能并不是一个最优的解决方案。此外,近年来,一些大学和研究机构开发了PPP处理服务,并通过互联网( APPS、GAPS、CSRS - PPP、Magic - PPP)在线发布( Guo 2015 )。这些在线服务通常用于PPP处理。然而,能够处理多GNSS数据的极少。另一方面,一些研究人员最近开始开发用于多GNSS PPP分析的开源软件包。例如,一个开源软件( GAMP )是RTKLIB的改进版,已被开发用于执行基于非差非组合观测值( Zhou et al 2018)的多GNSS PPP。然而,可以说,对于一个标准用户来说,软件的安装和使用并不容易。考虑到这一点,可以认为需要一个易于在每个用户级别使用,提供可靠解决方案,并在每个处理步骤中对用户的偏好开放的多GNSS PPP分析软件。
为了更好地利用多星座多频GNSS,我们开发了一个用户友好的GNSS分析软件PPPH。PPPH通过对GPS、GLONASS、BeiDou和Galileo数据进行后处理,可实现多GNSS PPP分析。得益于其图形用户界面( GUI ),PPPH允许用户加载GNSS数据源,确定多种处理选项和参数,并从多个角度对结果进行评估。MATLAB环境由于其基于矩阵的结构和内置的图形非常适合技术计算、编程和数据可视化,因此成为开发PPPH的首选环境。此外,MATLAB是全球科学家和工程师经常使用的编程环境之一,这意味着许多人可以很容易地访问该软件并扩展其功能。除MATLAB核心文件外,PPPH不使用任何与MATLAB分布的工具箱或函数。然而,由于该软件的图形用户界面( GUI )是使用MATLAB App Designer这一特殊环境来设计和开发用户界面的可视化组件的,因此需要MATLAB 2016a或更新版本。
下文首先阐述了多GNSS PPP的数学模型。随后,给出了PPPH的简要介绍。然后,给出了用于评估和验证PPPH性能的实验测试和结果。最后,提供了研究得出的结论。
3、多GNSS PPP建模
由于每个导航系统都利用自己的空间坐标系、时间尺度和信号结构,因此在进行多GNSS PPP处理时应考虑导航系统之间的差异。通常,通过坐标和/或时间变换来确保导航系统的互操作性。然而,当在同一参考系统和时间尺度内生成的精密轨道和钟差产品,如国际GNSS服务组织( IGS )产品,用于PPP数据处理时,系统间无需进行任何参考转换。虽然使用精密产品消除了坐标和时间基准的差异,但仍然需要处理接收机和卫星的硬件偏差( Cai和Gao 2013 )。
对于多GNSS PPP,码伪距( P )和载波相位( L )观测方程可以写成如下形式:

其中:

传统PPP依赖于从IGS网络获取的精密产品来消除卫星轨道和钟差。IGS精密卫星钟差产品是利用无电离层( IF )伪距观测值的线性组合生成的。相关的时钟偏差包括硬件码偏差(Kouba 和 Héroux 2001)。因此,卫星的硬件码偏差可以被纳入卫星时钟偏差中,并通过在IF线性组合中应用精密产品来去除。同样地,由于非差观测方程与接收机时钟高度相关,接收机硬件码偏差不能被估计,因此可以将其整合到接收机时钟偏差中。另一方面,无法利用IGS产品对接收机和卫星硬件相位偏差进行改正。因此,当对定位精度要求较低或可将其同化到模糊度参数中时,它们通常被忽略。对于第二种方案,模糊度参数不再是整数,因为它包含了硬件偏差(德弗雷涅和Baire 2011)。综合考虑,双频( i = 1 , 2)码伪距和相位观测值的IF组合可由( 3 )和( 4 )式形成:

与GPS、Galileo和BeiDou不同,GLONASS使用频分多址(FDMA)信号,这意味着每颗GLONASS卫星都有不同的频率通道和硬件偏差(Wanninger 2012)。因此,对于GLONASS,硬件偏差被表示为一个平均值和一个频率相关项的总和。频率相关项也称为频间偏差(IFBs)。
这里,由于卫星硬件码偏差由精密产品消除,卫星和接收机相位偏差与模糊度参数一起估计,因此只需考虑接收机硬件码偏差的IFB。码IFB项在PPP处理中可以被估计为额外的未知量,从而引起未知参数数量的显著增加。由于过多的参数削弱了模型结构,因此在处理过程中通常优先不估计码IFB。取而代之的是码伪距观测值相对于载波相位观测值要小得多的权重。因此,码IFB项可以忽略不计,其影响体现在码伪距残差( Cai和Gao 2013)上。
在(3)和(4)中,每个导航系统分别分配了一个接收机时钟偏差参数。为了简化处理,可以引入与GPS时钟偏差相关的GLONASS、Galileo和BeiDou系统时差参数,而不是估计不同的接收机时钟偏差。考虑到改正后的时钟偏差也包含硬件偏差,因此系统时差参数为相关导航系统与GPS的实际系统时差与硬件偏差( Cai和Gao 2013 ; Li et al . 2015)之和。应用精密产品并引入各系统关于GPS接收机钟差的系统时差参数后,GPS、GLONASS、Galileo和BeiDou的中频观测方程可写成如下形式:



4、PPPH:一款多GNSS PPP软件
PPPH是在MATLAB环境下开发的,用于集成多GNSS ( GPS、GLONASS、Galileo、北斗)数据进行PPP处理。从根本上说,PPPH旨在成为一个易用、健壮、高效的软件包。相应地,PPPH提供了一个用户友好的GUI来辅助用户选择导航文件、确定处理选项和分析结果。PPPH由5个主要组件组成,每个组件及其相关选项在GUI中用单独的选项卡表示。图1(与二、PPPH软件使用手册图一相同)展示了PPPH的操作流程图,包括主要组件及其功能。前4个组件利用相关模型和理论提供多GNSS PPP解决方案,最后一个组件用于评估和可视化结果。PPPH要求在进行后续操作之前,将执行PPP过程所必需的全部数据适当地导入到软件格式中。因此,在PPPH中,首先要定义包含标准导航数据的相关文件,如观测值、卫星轨道、钟差等。PPPH能够很好地处理标准的交换格式,包括RINEX、SP3、CLK和ATX,这些交换格式都应该在GUI的数据导入表中定义。
从导航文件中获得的原始数据在预处理步骤中进行处理,以防止可能出现的粗差和不一致。PPPH的预处理步骤包括异常值检测、周跳探测和钟差不一致性(钟跳)的确定。周跳采用两种不同的方法进行探测和修复,根据用户的偏好,可以单独使用,也可以组合使用。第一种方法根据Liu ( 2011 )使用Hatch - Melbourne - W ü bbena组合( Hatch 1982 ),第二种方法基于Deo和El - Mowafy ( 2015 )描述的无几何组合法。对于接收机钟差不一致性的判定,PPPH采用了Guo和Zhang ( 2014a )提出的方法。此外,根据用户的选择,相位平滑伪距和确定卫星截止高度角可以应用在这一步中。
PPPH中的建模部分用于减轻GNSS误差源对观测值的影响。在建模阶段,利用IGS机构提供的精密产品去除卫星轨道和钟差误差。利用无电离层线性组合消除了一阶电离层对GNSS观测值的影响。对流层延迟的干分量采用萨斯塔莫伊宁模型(萨斯塔莫伊宁1972 )进行改正,气象数据来源于Global Pressure and Temperature Model 2 ( Lagler et al 2013),湿分量在参数估计步骤中采用随机游走过程进行估计。全球映射函数( Boehm et al.2006)用于将天顶方向上模拟的对流层改正数投影到卫星高度角上,用于对流层延迟的干分量和湿分量。
对于GPS和GLONASS卫星,利用IGS绝对天线模型(例如, igs08 . atx或igs14 . atx)得到的值对天线相位中心偏差( PCO )及其变化量( PCV )进行改正;对于Galileo和BeiDou卫星,利用传统的PCO值对( Rizos et al 2013)进行改正。在接收机天线方面,GPS和GLONASS信号采用IGS绝对天线模型获取的PCO和PCV值。然而,由于相关模型中缺乏伽利略和北斗信号的PCO和PCV值,因此采用GPS值来修正这些系统的PCO和PCV。此外,相对论效应(Kouba 2015)、相位缠绕效应(Wu et al. 1993)以及包括固体地球潮汐和海洋负荷在内的站点位移效应(Petit 和 Luzum 2010)都根据标准方法进行修正。
关于估计过程,卡尔曼滤波器常被应用于导航问题的数据处理,它不仅提供了有关状态(即包含未知参数的向量)随时间变化的额外信息,还能够在使用的测量数量少于未知参数的情况下更新状态向量(Mohinder et al. 2007)。PPPH采用自适应抗差卡尔曼滤波方法,通过引入等效权矩阵补偿观测值中异常值的影响,同时引入自适应因子平衡量测和估计参数的权重,估计状态空间向量(郭庆旺、张军2014b)。卡尔曼滤波器需要对未知参数和测量进行统计定义,因为良好定义的统计特性为实现最优解铺奠定了基础。定义了未知参数的初始不确定度和谱密度以及测量噪声的默认值。然而,它们也可以由用户在PPPH GUI的Filtering Options选项卡中指定。
如前所述,由于FDMA信号的存在,GLONASS码观测值中含有IFB。优选对GLONASS码观测值赋予较小的权重,而不是在滤波过程中分别估计每个IFB。另一方面,由于Galileo和BeiDou的轨道和钟差产品相对于GPS产品( Montenbruck et al 2017 ; Guo et al 2017)质量较差,因此在滤波器中假定Galileo和BeiDou观测值精度较低。因此,在PPPH滤波过程中,GPS、GLONASS、Galileo和BeiDou观测值之间的标准差比设置如下:

在完成所有过程步骤后,PPPH为每个历元提供一个包含估计参数的结果文件。此外,通过GUI的Analysis选项卡,可以根据用户自定义的地面真值计算定位误差、均方根误差和收敛时间等过程统计量。为了评估估计参数及其统计量的单历元变化,PPPH能够产生若干曲线,例如定位误差、对流层天顶总延迟、接收机钟差估计、卫星数和DOP值。
5、实验测试和结果
为了验证和评估PPPH软件的性能,本文进行了两个实验测试。第1个试验旨在验证PPPH得到的结果与外部源的PPP估计值相比,第2个试验是评估多GNSS组合对PPP性能的影响。在这一部分中,描述了实验测试中使用的数据收集过程,并对结果进行了详细的展示。
从BKG (德国联邦地图局和大地测量局)数据中心获取了8个IGS站2017年7月9 - 15日1周的24 h观测数据集。观测数据的采样间隔为30 s。图2给出了8个IGS站的地理分布,8个IGS站为MGEX站,配备多GNSS接收机跟踪GPS、GLONASS、Galileo和BeiDou卫星。作为第一步,在仅包含GPS卫星的静态模式下,使用PPPH处理24 h数据集。同时,在GAPS ( GPS分析和定位软件http://gaps.gge.unb.ca/),是新布伦瑞克大学( UNB )开发的在线PPP服务) (莱安德罗等2011)中处理相同的数据集以验证PPPH结果。PPPH和GAPS所采用的处理策略见表1。(GPT2全球气压和温度2个数据,ECMWF欧洲中期天气预报中心数据,GMF全球映射函数,VMF维也纳映射函数)

图2 本研究使用的IGS站地理分布
表1 PPPH和GAPS中应用的处理策略

第一次测试从3D定位误差、均方根( RMS )误差和收敛时间三个方面进行统计评估。定位误差计算为相关PPP解与地面真值在相关处理时段(首次测试时间为24 h)结束时的差值。IGS周解被用作本研究的地面真值。另一方面,收敛时间被定义为达到亚分米级3D定位精度的时间,并持续超过10分钟。最后在本地系统(北、东、上)中计算所有历元相对于地面真值的收敛时间后的RMS误差。表2显示了所有实验测站在24小时处理结束时PPPH和GAPS估计获得的1周平均定位误差、RMS误差和收敛时间。所有测站PPPH和GAPS定位误差的平均值分别为13.3和15.0 mm。此时,由于对流层湿延迟估计不足和PPP误差源(如固体潮和海洋负荷)建模较弱,定位精度可能因测站的地理位置而异,因此测站之间存在一定差异。尽管如此,每个模型的结果与普遍接受的结果非常一致,并且考虑到PPP在静态模式下使用24小时数据集可以提供几厘米的位置精度。关于收敛时间,一般来说,大约50 min的收敛周期预计可以达到10 cm或更好的水平精度,这可能取决于用户环境(多路径)、地理位置和可见卫星的数量和几何形状。PPPH和GAPS提供的收敛时间的平均值分别为38.6和40.3 min,根据标准是合理的。最后,在考虑RMS误差的情况下,软件包之间的结果没有显著差异。综合考虑,可以认为PPPH软件的PPP性能与一般PPP标准和GAPS在线服务都具有可比性。
为了评估多GNSS组合对PPP性能的贡献,在GPS-only、GPS/GLONASS和多GNSS(GPS/GLONASS/Galileo/BeiDou)3种不同PPP模式下对同一数据集进行静态PPPH处理。但此时卡尔曼滤波估值器每3 h重新启动一次,每天提供8个时段,每个测站1周提供56个时段。为保持一致,所有系统均采用GFZ (德国地学研究中心)提供的精密轨道和钟差产品。同样地,从三维定位误差、RMS误差和收敛时间等方面对三种PPP模式的结果进行了分析。表3给出了3种不同PPP模式的平均定位误差、均方根误差和收敛时间,以及相对于纯GPS PPP解的改进情况。
在表3中,显然值得注意的是,使用附加星座与GPS一起大大增强了PPP在定位精度和收敛时间方面的性能。平均而言,GPS / GLONASS和多GNSS PPP模式分别将GPS单系统PPP定位精度提高了19.5 %和24.6 %。同样,可以观察到,与仅GPS的PPP解决方案相比,多GNSS组合在北、东和上方向的RMS误差有显著改善。此外,GPS / GLONASS和多GNSS PPP模式均缩短了GPS单系统PPP模式的收敛时间,平均改进量分别为27.4 %和33.1 %。虽然改善程度因测站而异,但包括GPS、GLONASS、Galileo和BeiDou在内的多GNSS PPP模式在各测站的定位精度和收敛时间上均表现最优。
表2 从PPPH和GAPS估计中获得的1周平均3D定位误差、RMS误差和收敛时间
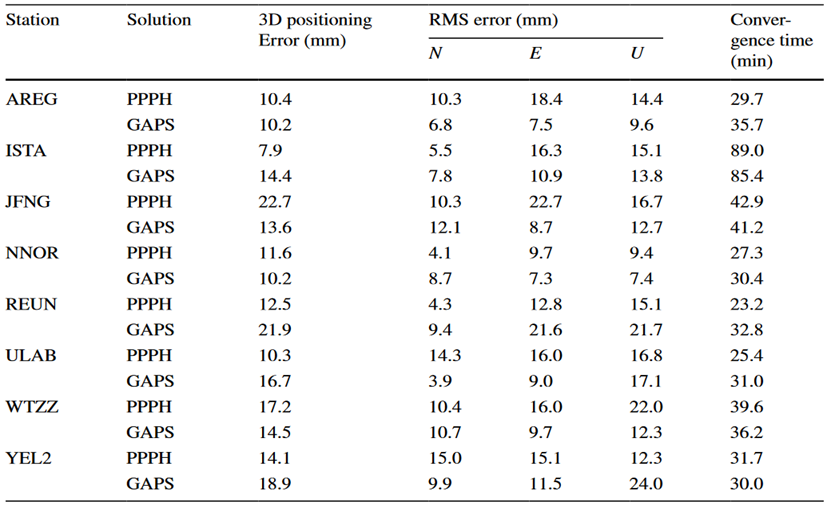
表3不同组合的平均定位误差、RMS误差和收敛时间及其相对于仅GPS解的改进

6、总结和结论
开发了基于MATLAB的用户友好型GNSS分析软件PPPH,用于集成多GNSS ( GPS、GLONASS、Galileo、北斗)数据进行PPP处理。PPPH能够为特定用户的多GNSS组合提供PPP解决方案。用户还可以在软件的GUI中指定选项、模型和参数。PPPH还提供了一个输出文件,分别包含每个历元的估计参数,并提供了一些分析工具对结果进行统计评估。虽然PPPH具有许多PPP处理的功能,但考虑到MATLAB环境是全球工程师和科学家最受欢迎的编程工具之一,PPPH的功能可以有效地扩展以满足高级用户的需求。
为了验证和评估PPPH的性能,进行了两个实验测试。首先,分别在PPPH和GAPS在线服务中处理了8个IGS站1周的24 h观测数据。从定位精度、均方根误差和收敛时间等方面对PPPH和GAPS进行了比较。结果表明,PPPH能够提供与一般PPP标准和GAPS相媲美的PPP解决方案。此外,还对多GNSS组合对PPP性能的潜在益处进行了统计评估。与单GPS PPP相比,GPS / GLONASS和多GNSS PPP ( GPS、GLONASS、Galileo、北斗)模式的定位精度平均提高了19.5 %和24.6 %。在收敛时间方面,GPS / GLONASS和多GNSS PPP模式相对于GPS单系统PPP解的平均改进分别为27.4 %和33.1 %。最终得出结论,多GNSS融合在定位精度和收敛时间上都显著提高了PPP性能。
考虑到在不久的将来,GNSS观测卫星的数量将继续增加,不同星座的集成为提高PPP性能提供了可观的前景。相应地,能够进行多GNSS PPP的GNSS分析软件包在GNSS领域的地位也越来越重要。PPPH为发挥多星座、多频GNSS的潜在优势提供了重要的可能。PPPH软件的MATLAB源代码、用户手册和样本数据可在http://www.ngs.noaa.gov/gps-toolbox/PPPH.的GPS Toolbox网站上获得。PPPH的内容和功能将继续改进,以便进一步应用。如有问题或建议,请随意与作者联系。
7、References
Boehm J, Niell A, Tregoning P, Schuh H (2006) Global Mapping Function (GMF): a new empirical mapping function based on numerical weather model data. Geophys Res Lett 33(7):L07304. https:// doi.org/10.1029/2005GL025546
Cai C, Gao Y (2013) Modelling and assessment of combined GPS/ GLONASS precise point positioning. GPS Solut 17(2):223–236. https://doi.org/10.1007/s10291-012-0273-9
Cai C, Gao Y, Pan L, Zhu J (2015) Precise point positioning with quadconstellations: GPS, BeiDou, GLONASS, and Galileo. Adv Space Res 56(1):133–143. https://doi.org/10.1016/j.asr.2015.04.001
Choy S, Bisnath S, Rizos S (2017) Uncovering common misconceptions in GNSS Precise Point Positioning and its future prospect. GPS Solut 21(1):13–22. https://doi.org/10.1007/s1029 1-016-0545-x
Defraigne P, Baire Q (2011) Combining GPS and GLONASS for time and frequency transfer. Adv Space Res 47(2):265–275. https://doi. org/10.1016/j.asr.2010.07.003
Deo M, El-Mowafy A (2015) Cycle Slip and clock jump repair with multi-frequency multi-constellation GNSS data for precise point positioning. In: IGNSS Symposium Gold Coast, Australia, July 14–16
Guo Q (2015) Precision comparison and analysis of four online free PPP services in static positioning and tropospheric delay estimation. GPS Solut 19(4):537–544. https://doi.org/10.1007/s1029 1-014-0413-5
Guo F, Zhang X (2014a) Real-time clock jump compensation for precise point positioning. GPS Solut 18(1):41–50. https://doi. org/10.1007/s10291-012-0307-3
Guo F, Zhang X (2014b) Adaptive robust Kalman filtering for precise point positioning. Meas Sci Technol 25(10):105011. https://doi. org/10.1088/0957-0233/25/10/105011
Guo F, Li X, Zhang X, Wang J (2017) The contribution of Multi-GNSS Experiment (MGEX) to precise point positioning. Adv Space Res 59(11):2714–2725. https://doi.org/10.1016/j.asr.2016.05.018
Hatch R (1982) The synergism of GPS code and carrier measurements. In: Proceedings of the third international symposium on satellite doppler positioning at physical sciences laboratory of New Mexico State University, vol 2, pp 1213–1231, Feb. 8–12
Hofmann-Wellenhof B, Lichtenegger H, Wasle E (2008) GNSSglobal navigation satellite systems. Springer, New York
Kouba J (2015) A guide to using international GNSS service (IGS) products. IGS website. https://kb.igs.org/hc/en-us/articles/20127 1873-A-Guide-to-Using-the-IGS-Products
Kouba J, Héroux P (2001) GPS precise point positioning using IGS orbit products. GPS Solut 5(2):12–28. https://doi.org/10.1007/ PL00012883
Lagler K, Schindelegger M, Böhm J, Krásná H, Nilsson T (2013) GPT2: Empirical slant delay model for radio space geodetic techniques. Geophys Res Lett 40(6):1069–1073. https://doi. org/10.1002/grl.50288
Leandro RF, Santos MC, Langley RB (2011) Analyzing GNSS data in precise point positioning software. GPS Solut 15(1):1–13. https://doi.org/10.1007/s10291-010-0173-9
Li X, Ge M, Dai X, Ren X, Fritsche M, Wickert J, Schuh H (2015) Accuracy and reliability of multi GNSS real-time precise positioning: GPS, GLONASS, BeiDou, and Galileo. J Geodesy 89(6):607–635. https://doi.org/10.1007/s00190-015-0802-8
Liu Z (2011) A new automated cycle slip detection and repair method for a single dual-frequency GPS receiver. J Geodesy 85(3):171–183. https://doi.org/10.1007/s00190-010-0426-y
Mohinder SG, Lawrence RW, Angus PA (2007) Global positioning systems, inertial navigation, and integration. Wiley, New Jersey Montenbruck O et al (2017) The multi-GNSS experiment (MGEX) of the international GNSS service (IGS)—achievements, prospects and challenges. Adv Space Res 59(7):1671–1697. https:// doi.org/10.1016/j.asr.2017.01.011
Petit G, Luzum B (2010) IERS conventions 2010 (IERS Technical Note; 36). Frankfurt am Main: Verlag des Bundesamts für Kartographie und Geodäsie, 2010, p 179, ISBN: 3-89888-989-6
Rizos C, Montenbruck O, Weber R, Neilan R, Hugentobler U (2013) The IGS MGEX Experiment as a milestone for a comprehensive multi-GNSS service. Proceedings of ION-PNT-2013, Institute of Navigation, Honolulu, USA, April 22–25, pp 289–295
Saastamoinen J (1972) Contributions to the theory of atmospheric refraction. Bulletin Geodesique 105(1):279–298. https://doi. org/10.1007/BF02521844
Seepersad G, Bisnath S (2014) Challenges in assessing PPP performance. J Appl Geodesy 8(3):205–222. https://doi.org/10.1515/ jag-2014-0008
Togedor J, Øvstedal O, Vigen E (2014) Precise orbit determination and point positioning using GPS, GLONASS, Galileo and BeiDou. J Geodetic Sci 4(1):65–73. https://doi.org/10.2478/ jogs-2014-0008
Wanninger L (2012) Carrier-phase inter-frequency biases of GLONASS receivers. J Geodesy 86(2):139–148. https://doi. org/10.1007/s00190-011-0502-y
Wu J, Wu S, Hajj G, Bertiger W, Lichten S (1993) Effects of antenna orientation on GPS carrier phase. Manuscripta Geodaetica 18(2):91–98
Yiğit C, Gikas V, Alçay S, Ceylan A (2014) Performance evaluation of short to long term GPS, GLONASS and GPS/GLONASS post-processed PPP. Survey Rev 46(336):155–166. https://doi. org/10.1179/1752270613Y.0000000068
Zhou F, Dong D, Li W, Jiang X, Wickert J, Schuh H (2018) GAMP: an open-source software of multi-GNSS precise point positioning using undifferenced and uncombined observations. GPS Solut 22:33. https://doi.org/10.1007/s10291-018-0699-9
Zumberge JF, Heflin MB, Jefferson DC, Watkins MM, Webb FH (1997) Precise pointpositioning for the efficient and robust analysis of GPS data from large networks. J Geophys Res Solid Earth 102(B3):5005–5017. https://doi.org/10.1029/96JB03860
























 1347
1347

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










