二分——图解+代码+例子（确定数的范围）

二分，通常指二分法或二分查找，是一种在有序数据集合中进行查找的高效算法。

基本原理：

1.对于给定的有序数组，首先选取数组的中间元素与目标值进行比较。

2.如果中间元素等于目标值，则查找成功，返回中间元素的索引。

3.如果目标值小于中间元素，那么目标值只可能存在于数组前半部分，接下来只需在前半部分继续进行查找。

4.如果目标值大于中间元素，那么目标值只可能存在于数组后半部分，接下来只需在后半部分进行查找。

重复上述过程，每次都将查找范围缩小一半，直到找到目标值或者确定目标值不存在数组中

二分模板：

//整数二分模版
int bsearch_1(int l,int r){
	while(l<r){
		int mid=(l+r+1)/2;
		if(check(mid)){
			l=mid;
		}
		else{
			r=mid-1;
		}
	}
	return l;
} 

int bsearch_2(int l,int r){
	while(l<r){
		int mid=l+r;
		if(check(mid)){
			r=mid;
		}
		else{
			l=mid+1;
		}
	}
	return l;
}
 

确定数的范围：

题目描述：

题目描述
给定一个按照升序排列的长度为n的整数数组，以及 q 个查询。
对于每个查询，返回一个元素k的起始位置和终止位置（位置从0开始计数）。
如果数组中不存在该元素，则返回“-1 -1”。
输入格式
第一行包含整数n和q，表示数组长度和询问个数。
第二行包含n个整数（均在1~10000范围内），表示完整数组。
接下来q行，每行包含一个整数k，表示一个询问元素。
输出格式
共q行，每行包含两个整数，表示所求元素的起始位置和终止位置。
如果数组中不存在该元素，则返回“-1 -1”。
数据范围
1≤n≤100000
1≤n≤100000

1≤q≤10000
1≤q≤10000

1≤k≤10000
1≤k≤10000

样例
输入样例：
6 3
1 2 2 3 3 4
3
4
5
输出样例：
3 4
5 5
-1 -1

本题是一个典型的二分查找，需要查找两个数第一个是>=x的第一个数，第二个是<=x的第一个数

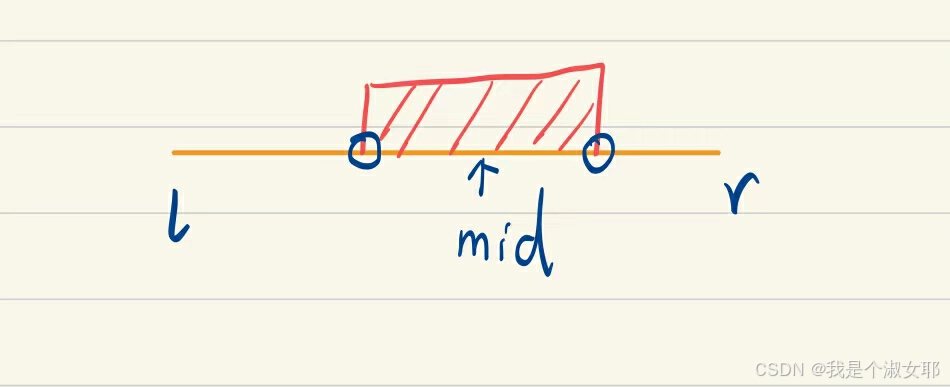
查找不小于x 的第一个位置：当a[mid]<x时，令l=mid+1,mid及其左边的位置被排除了，可能出现解的位置是mid+1及其后面的位置。当a[mid]>=x时，说明mid及其左边可能含有值为x的元素。当查找结束时，l与r相遇，l所在元素若是𝑥则一定是𝑥出现最小位置，因为𝑙左边的元素必然都小于𝑥。

要查找不大于x的最后一个位置：当a[mid]<=x时，待查找元素只可能在mid及其后面，所以l=mid;当a[mid]>x时，待查找元素只会在mid左边,另r=mid.

#include<stdio.h>
int main(){
	int q[100010]; 
	int n,m;
	scanf("%d %d",&n,&m);
	for(int i=0;i<n;i++){
		scanf("%d",&q[i]);
	}
	while(m--){
		int k;
		scanf("%d",&k);
		int l=0,r=n-1;
		while(l<r){
			int mid=(l+r)/2;
			if(q[mid]>=k){
				r=mid;
			}
			else{
				l=mid+1;
			}
		}
		if(q[l]!=k){
			printf("-1 -1");
		}
		else{
			printf("%d ",l);
			int l=0,r=n-1;
			while(l<r){
				int mid=(l+r+1)/2;
				if(q[mid]<=k){
					l=mid;
				}
				else{
					r=mid-1;
				}
			}
			printf("%d\n",l);
		}
		printf("\n");
	}
	return 0;
}