给定 n 个区间 [li,ri][],要求合并所有有交集的区间。
注意如果在端点处相交,也算有交集。
输出合并完成后的区间个数。
例如:[1,3][1,3] 和 [2,6][2,6] 可以合并为一个区间 [1,6][1,6]。
输入格式
第一行包含整数 n
接下来 n 行,每行包含两个整数 l和 r。
输出格式
共一行,包含一个整数,表示合并区间完成后的区间个数。
数据范围
1≤n≤1000001≤≤100000,
−109≤li≤ri≤109−109≤≤≤109
输入样例:
5
1 2
2 4
5 6
7 8
7 9
输出样例:
3
#include<iostream>
#include<algorithm>
#include<vector>
using namespace std;// 定义了一个名为 PII 的数据结构
//用来表示一对整数,代表区间的起始和结束位置。
typedef pair<int,int>PII;//pair储存两个int命名PII
const int N=100010;
int n;
vector<PII> segs;//
void merge(vector<PII>&segs)
{
vector<PII>res;//建立res存储新合并区间
sort(segs.begin(),segs.end());//按左端点排序
int st=-2e9,ed=-2e9;//
for(auto seg:segs)//seg为迭代变量,segs为被迭代的范围
//情况一:两个区间无法合并
if(ed<seg.first)
{
if(st!=-2e9)res.push_back({st,ed});//将区间1放进res数组
st=seg.first,ed=seg.second;//维护区间二
}
//情况二:两个区间可以合并||区间1不包含区间2,区间2也不包含2
else ed=max(ed,seg.second);
//实际情况三(区间1包含区间2)因为是按左排序不可能有区间2包含1
if(st!=-2e9)
res.push_back({st,ed});
////考虑循环结束时的st,ed变量,此时的st,ed变量不需要继续维护,只需要放进res数组即可。
//因为这是最后的一个序列,所以不可能继续进行合并。
segs=res;
}
int main()
{
cin>>n;
for(int i=0;i<n;i++)
{
int l,r;
cin>>l>>r;
segs.push_back({l,r});//存储到区间向量中
}
merge(segs);
cout<<segs.size()<<endl;
return 0;
}
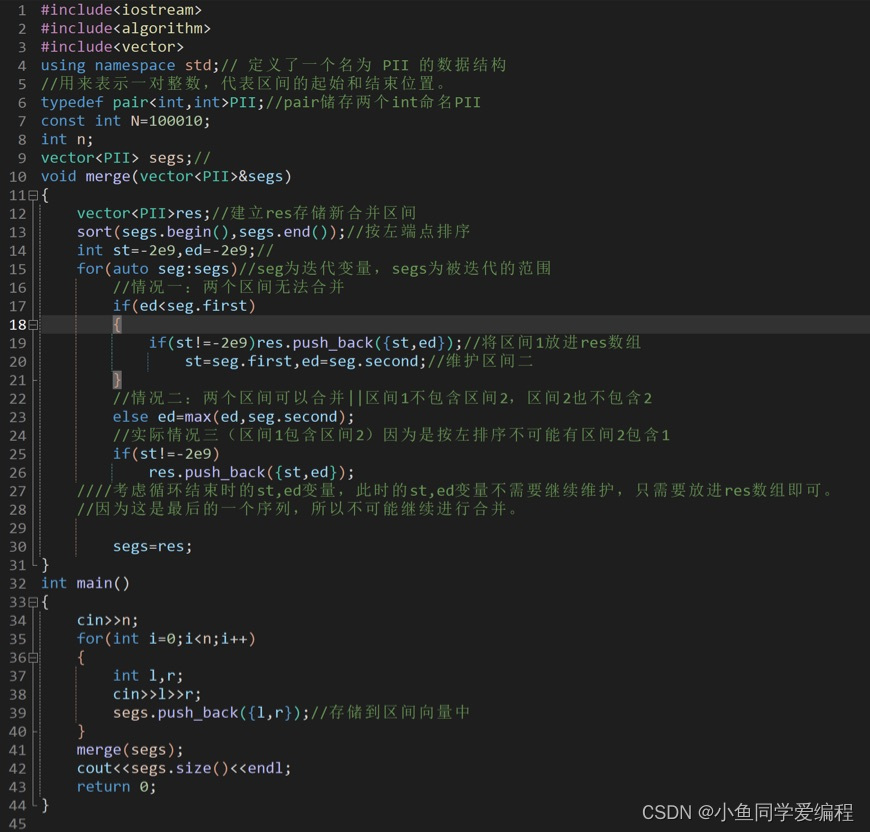




 文章介绍了一种在C++中处理区间合并问题的方法,通过先排序再合并,以求得最终合并后区间的个数。
文章介绍了一种在C++中处理区间合并问题的方法,通过先排序再合并,以求得最终合并后区间的个数。
















 2082
2082

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








