这一节我们参考李沐老师的教程(没看过也没关系),由表及里,从零带你构建出整个框架,
不仅教你代码实现,更告诉你为什么这么做!
这样无论搭建什么深度学习的框架,我们都能得心应手。
同学们看过书后一个印象肯定是
“为什么我貌似看懂了却自己复现不了?”
“他怎么想的这样写?”
“为什么我漏模块了”
很重要一个原因就是绝大多数教程是顺序讲解,而我们的理解方式却不是这样:
我们读代码第一步是明确我们要做什么——确定输出,再看看得到这些输出需要什么——确定输入,最后才是确定如何操作才能由输入得到输出。
就好比你要做菜,你先要确定你要做什么菜系的哪道菜,再确定需要买什么食材,最后再看是先炸后焖还是先炖后红烧对吧~
以上就是我希望这一节能带给你的最重要的启示。
此外,书上的代码对于小白来说还是略显抽象,我们这一节提供比书上更详细的代码解释并附上我的手绘图。
基础参数
小白也能听懂行话:
模型 就是 拟合函数。
训练模型 就是 找到拟合函数的参数。
特征(x) 就是 输入的自变量,也就是输入数据。
标签(labels) 就是 真实值。
偏差(b) 就是 固定常数。
权重(ω) 就是 输入的自变量对结果的影响程度。
噪声 就是 随机波动。
线性回归的框架搭建?——为什么这么做?
我从思路给客官缕一缕:
整体思路
需要输出什么:
线性回归本质就是找一条线/曲线,去拟合实际的变化曲线。
找这条线,就是确定这条线的方程参数。
那么输出这些参数需要什么:
你可能认为我们只有数据集,其实,
我们还有一个已知要使用线性回归的模型。
最后是如何完成这个过程:
从输入出发:
训练集往往存着的是图片、音频这类非二进制数据,首先先要将这些数据转换为模型可读取的格式。——预处理
模型无法一次接收这么多数据,因此要分批传入。——数据输入
对于线性模型(一个函数),在此之前还应该完成定义模型 并 完成初始化。
从输出出发:
我们的输出是最合适的参数,显然这些参数是让模型自己去找的,我们要做的就一件事
衡量找得准不准,于是我们需要一个评估误差的东西——损失函数。
得到这个误差我们肯定要通过优化参数减小误差,于是需要建立误差和方程参数的关系——优化函数。
不断进行这个过程,就能得到我们需要的参数。
以上,就是我作为小白完成框架搭建的思考过程,希望你也可以理解。

如何写线性回归?——如何做?
我们依然是从输入开始思考:
一、预处理——生成数据集
线性回归我们可以手搓数据集。我们依然锻炼从目的找手段的思维。
输出:一个数据集,包括 自变量矩阵X 和 真实值矩阵Y,X用于训练获取预测值,Y用于评估。
输入:自变量个数x_num、样本数量n、真实的权重
、真实的偏置
。
步骤:通过
构建输入到输出的关系。
当然我们不能笔算n个
得到X和Y。
因此我们提供公式让计算机把数据集造出来。
① 首先定义这些输入参数:
自变量的个数x_num = 2 样本个数n = 1000 自变量对应的权重ω = [2, -3.4] 波动值b = 4.2显然n组数据不可能一个一个存储,我们想到了矩阵存储。
② 于是我们定义装自变量x的容器,以及装真实值y的容器:
装自变量x的容器 = torch.randn(样本个数, 自变量的个数)装真实值y的容器 = torch.zeros(样本个数, 1)括号里的参数就是这个矩阵的大小,里面长这样:
③ 接着可以让计算机自行将真实值y生成出来,存储在装y的容器中:
刻画公式y=ω1x1+ω2x2+b,其中参数都是矩阵形式:
装真实值y的容器 = ω[0] * 装x的容器[:, 0] + ω[1] * 装x的容器[:, 1] + 偏置b将x容器的第一列与权重ω1相乘,将x容器的第二列与权重ω2相乘,有图应该看得懂吧~
④ 最后再加点噪声(随机波动),给模型上上难度!(否则就是数值解了)
装y的容器 += torch.tensor(随机值np.random.normal(0, 0.01))这句话就是生成均值为0,方差为0.01的随机正态分布,其他参数先不管。
官方代码,和我们讲的是基本一样的:
num_inputs = 2 num_examples = 1000 true_w = [2, -3.4] true_b = 4.2 #定义基础参数 features = torch.randn(num_examples, num_inputs, dtype=torch.float32) #制造容器矩阵X labels = true_w[0] * features[:, 0] + true_w[1] * features[:, 1] + true_b #根据参数生成真实值矩阵Y labels += torch.tensor(np.random.normal(0, 0.01, size=labels.size()), dtype=torch.float32) #为每个真实值y添加随机波动
二、输入数据/读取数据
输出:指定大小的两种数组 一个是自变量X 一个是真实值Y,X用于训练获取预测值,Y用于评估。
输入:生成的数据集 装自变量x的容器 和 装真实值y的容器 以及 单次投入的数量
def 数据遍历器(单次投入数量, 自变量x矩阵, 真实值y矩阵): //实现逻辑 return 单次自变量x矩阵, 单次真实值y矩阵从这个函数声明很容易得知,
步骤:按照投入数量拆解数据集,并按照这个大小返回单次X和Y矩阵。
① 打乱
在拆解前我们思考一个问题,这几天你一直做第一类曲线积分,结果考试考了第二类曲线积分,是不是有思维惯性做错。模型也一样,如果我们的数据集是前一半是A类,后一半是B类,很容易发生过拟合的现象。
于是你们老师给你做套卷,打乱题型。这就是解决的办法——打乱原始顺序!
random.shuffle(数据的索引index)但是,突然发现,我们输入的X、Y矩阵没有对应的索引,很简单,我们为他加上:
index = list(range(数据集大小n)) random.shuffle(数据的索引index)range函数自动生成一个 数据集大小n 的 整数序列,list函数将这个序列转换为我们更方便操作的列表类型。
② 拆解:
由于我们打乱了索引顺序,因此拆解后返回对应的索引有点难。
一开始我们的矩阵是
,打乱后可能变成
,
假如我们按3个一批取,取得的就是索引为[11][45][14]这三项对应的XY矩阵。
难点就变成了如何从X、Y矩阵中取出[11][45][14]对应的这几条数据。
好在,PyTorch为我们准备了工具——index_select(q1,q2)
参数q1=0代表选择列,q2是这一列要选取的对象。
问题迎刃而解。
我们用 j列表 存储每批要输出的索引,再用index_select选中XY列表中对应的行输出即可:
for i in range(从0到数据大小n,每次输出p个): j = 包含这p个索引的列表 return 对X矩阵.index_select(0, j), 对Y矩阵.index_select(0, j)以上是形象的匹配-输出过程,希望你能理解。
官方代码是不是义眼定真了:
#n是第一节全局参数定义的数据集大小 def data_iter(批次大小p, 自变量矩阵X, 自变量矩阵Y): n = len(X) #得到样本长度 相对于传入 数据集大小n index = list(range(n)) #生成索引列表 random.shuffle(index) #打乱顺序 防止过拟合 for i in range(0, n, p): j = torch.LongTensor(index[i: min(i + p, n)]) #防止越界 yield X.index_select(0, j), Y.index_select(0, j) #返回索引对应j列表的数据行 yield是返回一批 因此不用return了
三、定义/初始化模型
非常好,数据模块你已经完全掌握了!接下来处理模型模块。
定义模型就是构建一个函数,构建之前可以完成参数的初始化。
输入:初始化参数
、
输出:线性模型
步骤:先初始化,再带入
① 初始化
我们自己引入最初的
、
:
采用0为均值,0.01为方差的正态分布,由于是矩阵计算生成(n,1)大小的矩阵。
采用全赋0:
w = torch.tensor(权重随机值np.random.normal(0, 0.01, (n, 1))) b = torch.zeros(1, )Q:有的小伙伴抛出疑问:为什么权重w不能初始化为0呢?
因为这样每个神经元的梯度是相同的,导致参数更新方式完全一致。
Q:又有人问(1,)这个逗号后面咋没东西?
这是最基础的语法,为了分辨普通括号与元组,一维的元组必须加逗号,别忘了~
② 构建模型
构建模型,也要用矩阵实现!
那么
就是
的矩阵表达。
我们可以用matrix multiply (torch.mm)函数实现矩阵乘法。
def 线性模型(X, w, b): return torch.mm(X, w) + b官方代码:
w = torch.tensor(np.random.normal(0, 0.01, (num_inputs, 1)), dtype=torch.float32) b = torch.zeros(1, dtype=torch.float32) #初始化ω、b def linreg(X, w, b): return torch.mm(X, w) + b #构建模型 w.requires_grad_(requires_grad=True) b.requires_grad_(requires_grad=True)最后这两行是什么,我们一会再说~
四、定义损失函数
定损需要参照,因此我们从数据输入进来的Y实际值矩阵就有用啦~
输入:Y实际值矩阵、
预测值矩阵
输出:误差值
步骤:找一个合适的函数显示误差
def 损失函数(Y, Y_hat): return (Y_hat - Y)) ** 2 / 2除了squared还有MSE、MAE、HuberLoss这些损失函数,在此我们采用相对简单的示例。
上官方代码:
def squared_loss(y_hat, y): return (y_hat - y.view(y_hat.size())) ** 2 / 2 l.backward()view函数是为了统一矩阵的大小和y_hat一样方便矩阵运算。
最后这行是什么,我们一会再说~
五、定义优化算法
第一轮训练误差值一般很大,因此需要通过调节参数ω和b减小参数,就需要优化算法。
上一步我们得到了误差(损失函数),如果能找到误差(损失函数)与我们要更新的ω、b的关系,是不是就能通过调整ω和b减小误差了?
因此我们考虑损失函数对ω或b求导,得到 误差对于ω或b增加的方向和大小,我们反其道而行之,就能减小误差。
输出:新的ω和b
输入:更新的程度lr、包含ω和b的参数矩阵、损失函数
步骤:分别从参数矩阵取出要更新的ω和b,依次更新。
① 求导
那么核心的目的就是求导了。
在神经网络中,我们往往会对ω和b做很多变换,
误差(损失函数)与ω、b之间的关系无法通过直接求导得到。
那么,如何获取这个导数呢?
我们想到高数中的链式求导法则,将中间过程看作复合函数,如图所示:
最上面的节点代表损失函数f(x),两个叶子节点分别代表我们要求导的变量ω和b,分别通过中间函数g(ω),h(b)与损失函数f(x)复合,由链式法则,得到图中的式子。
化简后发现——我们只要知道了①最底层的导数 以及 ②g(ω)、h(b)的运算操作,就能得到损失函数f(x)关于ω、b和导数。
那么问题就在于如何获取最底层的导数,以及对其的运算操作上了。
在PyTorch中,有个对象叫张量,ω、b的矩阵也是一种张量。
张量有一些属性可以帮我们实现:
.requires_grad是一个记录运算操作的开关,当requires_grad=True时则开始追踪(track)在这个参数(ω、b)所有操作。
完成记录后,可以调用.backward()来自动完成所有导数计算。
于是我们想到流程应该如下:
先打开运算操作记录开关 w.requires_grad_(requires_grad=True) b.requires_grad_(requires_grad=True) 再计算损失函数 Loss = 损失函数(Y, Y_hat).sum 接着求损失函数对ω、b的导数 l.backward() 最后得到了Loss关于ω和b的导数后调用优化函数因此打开运算记录开关的操作,就放在第三模块的最后两行了!
求导的这一步就放在第四模块的最后一行了!
② 更新
我们得到了导数,接下来考虑如何通过损失函数对ω、b的导数更新ω和b。
我们使用最简单的梯度下降方法,也叫下山法:
损失函数(蓝色)就是这座山,橙色是损失函数关于ω、b的导数,我们通过每次沿着下山方向走一段距离红色箭头(学习率),看看是不是最低点,持续这个过程就可以找到最小值了。
公式是:
α是学习率,为什么会有这一项呢?
好比你一步一步走下山,很大概率能沿着山谷走到最低点;
如果你是跑步下山,可能在最低点一脚就迈过去了,略过了最小值。
一言以蔽之,更新就是要实现:
新的ω或b = 旧的ω或b 减去 (更新的幅度 乘以 更新的方向)
伪代码复现:
def 优化函数(参数矩阵, 更新幅度): for ω/b矩阵 in 参数矩阵: return ω/b矩阵 -= 更新幅度 * 损失函数对ω/b的导数官方代码如下:
def sgd(params, lr, batch_size): for param in params: param.data -= lr * param.grad / batch_size #batch_size在损失函数写也可以
六、训练模型
恭喜你,看到最后一部分啦!!!
还记得我们在板块二定义的传入批次的大小,板块五引入的更新幅度(学习率),以及总共的训练批次吗?
记得将他们也引入!
更新幅度α = 0.03 训练批次 = 3 单次训练数量p = 10输入:各个模块+思考过程中新加入的参数
输出:拟合最接近的ω和b,以及其与真实值的误差(依然存在)
过程:如下:
① 首先调用模块二的数据遍历器,传入自变量矩阵X和真实值矩阵Y,以及单次训练的数量p。
for epoch in range(训练批次): for X, y in 数据遍历器(p单次训练数量, X自变量矩阵, Y真实值矩阵):② 再调用模块三构建的线性模型,将①的自变量矩阵X、参数ω、b传入,输出预测值y_hat。
for epoch in range(训练批次): for X, y in 数据遍历器(p单次训练数量, X自变量矩阵, Y真实值矩阵): y_hat预测值 = 线性模型(X, w, b)③ 再调用模块四构建的损失函数,将②算出的预测值与实际值对比输出误差l。
并调用l.backward(),计算出损失函数对ω、b的导数。
for epoch in range(训练批次): for X, y in 数据遍历器(p单次训练数量, X自变量矩阵, Y真实值矩阵): y_hat预测值 = 线性模型(X, w, b) l = 损失函数(y_hat预测值, y真实值).sum() # 计算损失函数 l.backward() # 计算损失函数关于ω、b的导数④ 再调用模块五构建的优化函数,更新参数ω和b。
for epoch in range(训练批次): for X, y in 数据遍历器(p单次训练数量, X自变量矩阵, Y真实值矩阵): y_hat预测值 = 线性模型(X, w, b) l = 损失函数(y_hat预测值, y真实值).sum() # 计算损失函数 l.backward() # 计算损失函数关于ω、b的导数 优化函数([w, b]待更新参数列表, α更新幅度)⑤ 每轮训练都需要将上一轮记录的损失函数对ω、b的导数清零,否则下一轮就会加上这一轮的更新程度了(梯度重叠冲突)
for epoch in range(训练批次): for X, y in 数据遍历器(p单次训练数量, X自变量矩阵, Y真实值矩阵): y_hat预测值 = 线性模型(X, w, b) l = 损失函数(y_hat预测值, y真实值).sum() # 计算损失函数 l.backward() # 计算损失函数关于ω、b的导数 优化函数([w, b]待更新参数列表, α更新幅度) # 导数清零 w.grad.data.zero_() b.grad.data.zero_()⑥ 最后是评估本轮训练的情况 并输出对应的ω和b。
for epoch in range(训练批次): for X, y in 数据遍历器(p单次训练数量, X自变量矩阵, Y真实值矩阵): y_hat预测值 = 线性模型(X, w, b) l = 损失函数(y_hat预测值, y真实值).sum() # 计算损失函数 l.backward() # 计算损失函数关于ω、b的导数 优化函数([w, b]待更新参数列表, α更新幅度) # 导数清零 w.grad.data.zero_() b.grad.data.zero_() #验证本轮更新效果 train_l = 损失函数(线性模型(自变量矩阵X, 本轮的w, 本轮的b), 真实值矩阵Y) print('epoch %d, loss %f' % (epoch + 1, train_l.mean().item())) print(true_w, '\n', w) print(true_b, '\n', b) 输出: epoch 1, loss 0.028127 [2, -3.4] tensor([[ 1.9998],[-3.3998]], requires_grad=True) 4.2 tensor([4.2001], requires_grad=True)本节最后一次把官方代码奉上:
lr = 0.03 num_epochs = 3 net = linreg loss = squared_loss for epoch in range(num_epochs): # 训练模型一共需要num_epochs个迭代周期 # 在每一个迭代周期中,会使用训练数据集中所有样本一次(假设样本数能够被批量大小整除)。X # 和y分别是小批量样本的特征和标签 for X, y in data_iter(batch_size, features, labels): l = loss(net(X, w, b), y).sum() # l是有关小批量X和y的损失 l.backward() # 小批量的损失对模型参数求梯度 sgd([w, b], lr, batch_size) # 使用小批量随机梯度下降迭代模型参数 # 不要忘了梯度清零 w.grad.data.zero_() b.grad.data.zero_() train_l = loss(net(features, w, b), labels) print('epoch %d, loss %f' % (epoch + 1, train_l.mean().item())) print(true_w, '\n', w) print(true_b, '\n', b)
!!!!!完结撒花,恭喜毕业!!!!!
从此,你无论是做更难的分类softmax问题还是用其他框架做训练,脑子里都会复现这样的框架。
更重要的是,哪怕你完全忘记这个框架时,你仍然掌握了我的核心构建方法
——从目的找手段,从数据推手段,双向奔赴的核心思维。
也完全可以手搓一个框架~
小总结:
本节详尽地从介绍框架的基础参数到在脑海中构建一个框架体系,最后再用代码将其实现。
不仅包括如何写,更重视为什么这么做的思考过程。
最重要的是提供了一种读懂代码,思考如何写代码的思维。
写在后面:
当然,我在第六板块也提到了一个你需要尽快补上的环节——梯度与反向传播原理。之前的专栏也放在这里啦:
梯度是什么?梯度下降是什么?为什么要用梯度?如何用PyTorch自动求梯度?-优快云博客
深度学习模型参数是如何更新的?什么是梯度累计?为什么要梯度累计?-优快云博客
我相信你在读完这两节后会对整个深度学习的基本框架有一个深入且完备的理解。
想跑通的话,可以去官方网址下载项目,星马更注重教你如何构建出整个框架,再一点点填上去,知其然,也知其所以然。
很开心你能耐着性子读到这里,很荣幸能将我的三脚猫知识分享给大家,之后的学习也祝你好运。
星马也是小白,因此更懂小白的心思,大佬认为一眼明白的代码和思路可能在我们眼中就是鸿沟。这篇文章也还有很多不足之处,或是纰漏,希望你发现了及时在评论区提醒我呀~
(人工智能学院就是每周四五天满课的啦,因此更新基本随缘~)
八千字 + 自己画的图 别丢收藏夹吃灰啦好嘛~
参考资料是李沐老师的:Dive-into-DL-PyTorch
星马是刚入门的大菜比,有错望指正,有项目可以带带我。
目录放在后面方便复习~
目录












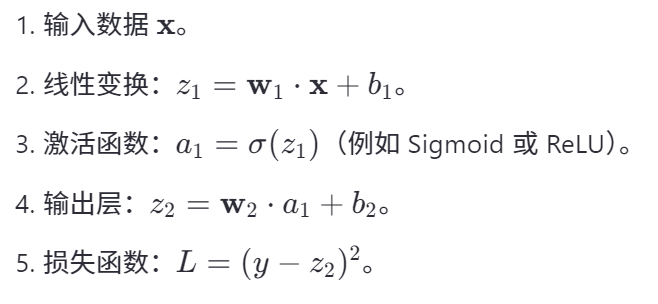



















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








