每日一题（JAVA）

环形真假谎言

问题描述

在风景如画的蓝桥村，nn 名村民围坐在一张古老的圆桌旁，参与一场思想的较量。这些村民，每一位都有着鲜明的身份：要么是誉满乡野的诚实者，要么是无可救药的说谎者。

当会议的钟声敲响，一场关于真理与谬误的辩论随之展开。每位村民轮流发言，编号为 ii 的村民提出了这样的断言：坐在他之后的两位村民 — 也就是编号 i+1i+1 和 i+2i+2（注意，编号是环形的，所以如果 ii 是最后一个，则 i+1i+1 是第一个，以此类推）之中，一个说的是真话，而另一个说的是假话。

在所有摇曳不定的陈述中，有多少真言隐藏在谎言的面纱之后？

请你探索每一种可能的真假排列组合，并计算在所有可能的真假组合中，说谎者的总数。

输入格式

第一行输入一个整数 TT，表示数据的组数。

接下来 TT 行，每行包含一个整数 nn，表示村落的人数。

输出格式

对于每组数据，输出一行包含一个整数，表示答案。

思路

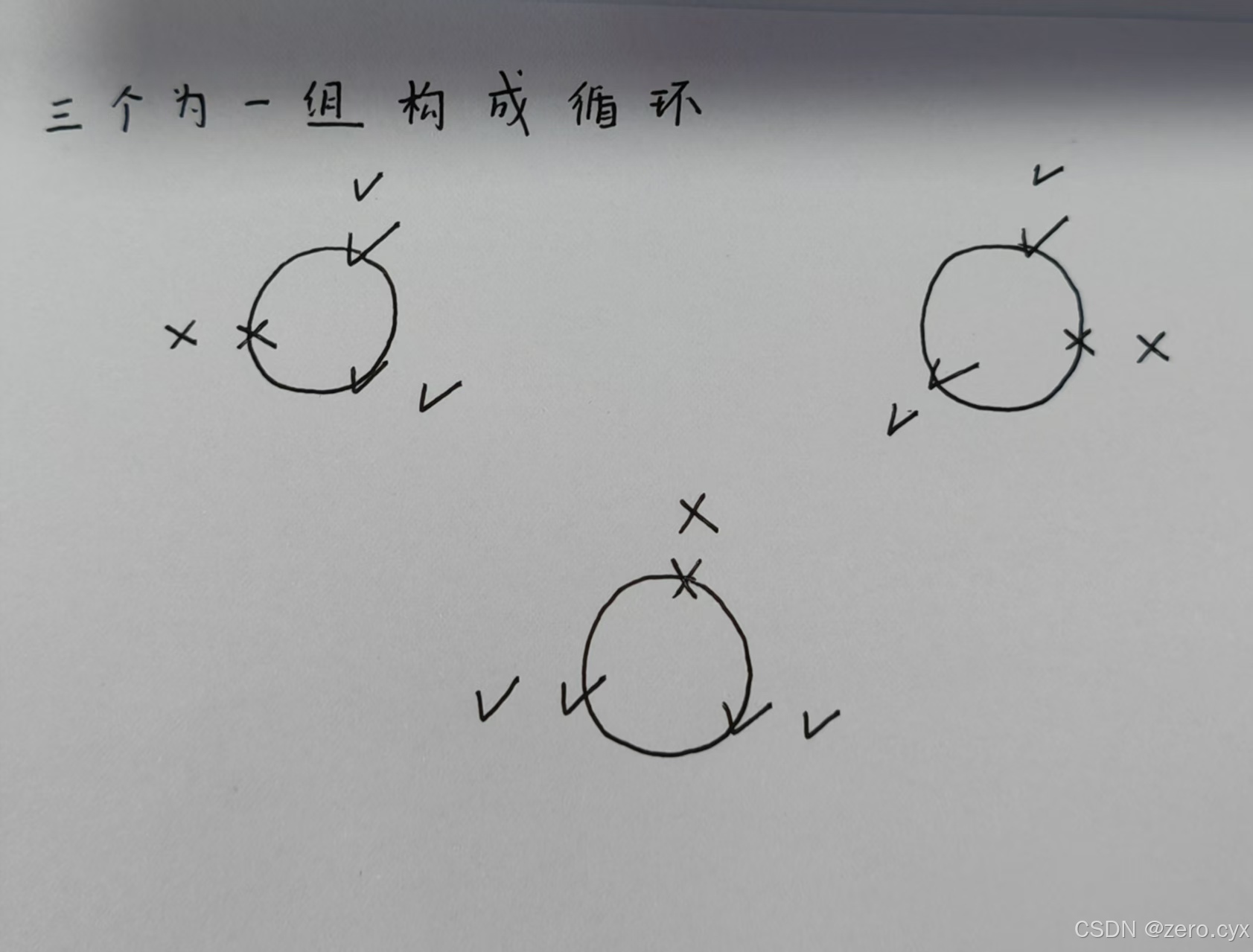
这道题目的欺骗性在于，题目所说的断言这个人，可能说了真话，也可能说的是假话。如果是假话对应第二个图，真话就是第一个图，因此答案是6.

分为下图三种情况，或者全部为x.

import java.util.Scanner;
// 1:无需package
// 2: 类名必须Main, 不可修改

public class Main {
    public static void main(String[] args) {
        Scanner s = new Scanner(System.in);
        //在此输入您的代码...
        int t = s.nextInt();
        while(t-- > 0) {
          long n = s.nextLong();
          long res = n;

          if(n % 3 == 0){
              res += n;
          }

          System.out.println(res);
        }
        s.close();
    }
}