前言
位图实际上就是运用哈希的思想将内存极致的利用,尽可能地提升效率。哈希的关键就是建立映射关系,提供高效的访问,下面我们来看到面试题。
给40亿个不重复的无符号整数,没排过序。给一个无符号整数,如何快速判断一个数是否在 这40亿个数中。【腾讯】
首先想到的就是将这40亿个数进行排序,然后进行二分查找,快速排序时间复杂度为O(NlogN),二分查找一次为O(logN)。这种方法在时间复杂度层面还是不错的,但空间复杂度相对来说是比较高的,下面我们来计算下上述算法需要多少内存。
40 0000 0000 *4 /1024 /1024 /1024 大约等于15 G,我们普通计算机如今只有16的内存,硬盘大小可扩充,但程序是在内存上运行的,也就是说运行上述程序可能使我们的内存爆满,如果内存不够就会崩溃!!。
我们可以先思考如下分割后的简单小问题。
假如是如下情况 int a[] = { 5,6,3,8,4,9 };判断一个数是否在 这6个数中,我们可以开辟一个大小为10的bool数组,如下图。数组初始化全为假即0

遍历数组,将该数对应位置设置为true即1,这样判断某个数在不在数组中,就可以直接访问数组对应下标位置即可,每次查询的效率为O(1),建立了一种哈希映射。

我们在回过头看上面的例子,对于每个数他只有两种情况,在与不在,可以用0与1表示,而bool类型为1字节,但一个比特位就可以表示0与1两种状态,相当于每个bool类型我们浪费了7个比特位。
于是我们便引入位图的概念,用一个比特位表示两者状态,这样就充分利用每一块空间,此时再处理上述的面试题空间大概占用 4,294,967,295/8 /1024 /1024 /1024 大约等于0.5 G!查询的效率也达到了恐怖的O(1),十分的高效。
接下来我们来实现位图。
位图实现
在C++中一般个人使用最小的内存大小为字节,而位图则是对比特位进行操作,我们不能直接的开辟60位出来,但我们可以间接的开辟出比特位。
假如我们需要60位,我们开辟两个无符号整型数组,一个无符号整型大小为32位,两个位64位满足我们的需求,接着就是找打第60位。

面对数字60,我们可以通过下面除与模来找到他的具体位置
int i = x / 32;
int j = x % 32;例如60/32=1,那么60在bs[1]数中,60%32=28,那么60就在bs[1]下标28处,由此我们便可以找到每个数对应的比特位。相当于我们把数组中每一个无符号数看为一个小数组,由32个比特位组成。
经过上述分析我们就可以写出如下框架
#pragma once
#include<iostream>
#include<vector>
using namespace std;
template<size_t N>
class bit_set
{
public:
bit_set()
{
//这里加一解决出现31/32=0或者32/32=1不足的情况
_bs.resize(N / 32 + 1);
}
private:
vector<size_t> _bs;
};其中我们采用了模板参数传递最大值是多少,然后 计算要开辟多大数组。(模板除了传递类型,还可以传递具体的参数)。
接下来我们实现位图中几个重要的函数。
set
set就是将数对应位置比特位设置为1
//将对应位设置为1
bit_set& set(size_t x)
{
}给我们一个数,如何将对应位置设置为1?这里就要用到位运算。 如下图

于是我们便可以完成函数操作。
//将对应位设置为1
bit_set& set(size_t x)
{
int i = x / 32;
int j = x % 32;
_bs[i] |= (1 << j);
return *this;
}reset
reset就是将数对应位置比特位设置为0.原理如下图。

那么现在的问题就是如何得到第j位为0,其余为为1的数?通过观察我们可以发现只要将原来1左移j位的值取反即可得到目标值。
于是我们便可以完成函数操作。在位运算时能加括号尽量加上括号,否则可能由于运算符优先级形成错误问题。
//将对应位设置为0
bit_set& reset(size_t x)
{
int i = x / 32;
int j = x % 32;
_bs[i] &= (~(1 << j));
return *this;
}test
test是用来检测当前数对应为是否为1的,当前位为1返回真否则返回假,原理如下

//当前位为1返回真否则返回假
bool test(size_t x) const
{
int i = x / 32;
int j = x % 32;
return _bs[i] & (1 << j);
}计数
最后就是两个关于计数大小的函数,第一个返回当前支持多少位,第二个返回有多少位为1
size_t size()
{
return N;
}
//返回1的个数
size_t count()
{
size_t ret = 0;
for (int i = 0; i < N; i++)
{
if (test(i))
ret++;
}
return ret;
}位图的效率十分高,但主要适用于整数,对于一些其他的类型无法很好的映射。一些场景可以使用布隆过滤器,来达到位图的高效。
题目
387. 字符串中的第一个唯一字符 - 力扣(LeetCode)
最后做个题目练习一下。

这里开辟一个位图是不够的,我们要表示每个数的状态有0 1 多次三种,就可以开辟两个位图来处理。先遍历一遍处理位图,再遍历一遍寻找出现一次的数字
class Solution {
public:
int firstUniqChar(string s)
{
bitset<26> bs1; // 0(0次) 1(1次)
bitset<26> bs2;// 1(多次)
//先遍历一遍统计次数
for (int i = 0; i < s.size(); i++)
{
char ch = s[i] - 'a';
bool flag1 = bs1.test(ch);
bool flag2 = bs2.test(ch);
if (!flag1 && !flag2)// 0 0
{
bs1.set(ch);
}
else if (flag1 && !flag2)// 1 0
{
bs2.set(ch);
}
else// 多次出现 不处理
{
// 1 1
}
}
for (int i = 0; i < s.size(); i++)
{
char ch = s[i] - 'a';
bool flag1 = bs1.test(ch);
bool flag2 = bs2.test(ch);
if (flag1 && !flag2)// 1 0
{
return i;
}
}
return -1;
}
};VS开辟大小细节问题
我们自己实现的bitset大小可以开辟出无符号整型最大值,但STL模板实现的不可以如下图。
STL实在栈区开辟的数组,而栈区通常只有8M左右,开辟这么大内存会栈溢出,所以下面错误是stackoverflow。而我们自己写的是在堆区申请内存,堆区足够大可以申请出来。
自定义版本
对于我们自己实现的bitset在堆区开辟可以通过打印地址来验证。 此时将类中vector权限放开,改为public,否则报错
void test2()
{
bit_set<100> bs1;
int* p = new int(4);
int c = 0;
cout <<"p :" << (void*)p << endl;
cout << "bs1:" << (void*)&bs1._bs[0] << endl;
cout << "c :" << (void*)&c << endl;
}通过上图可以发现bs1开辟数据存储的地方例栈区c比较远,但离堆区开辟的p近,由此便可证明我们实现的在堆区开辟。
STL版本
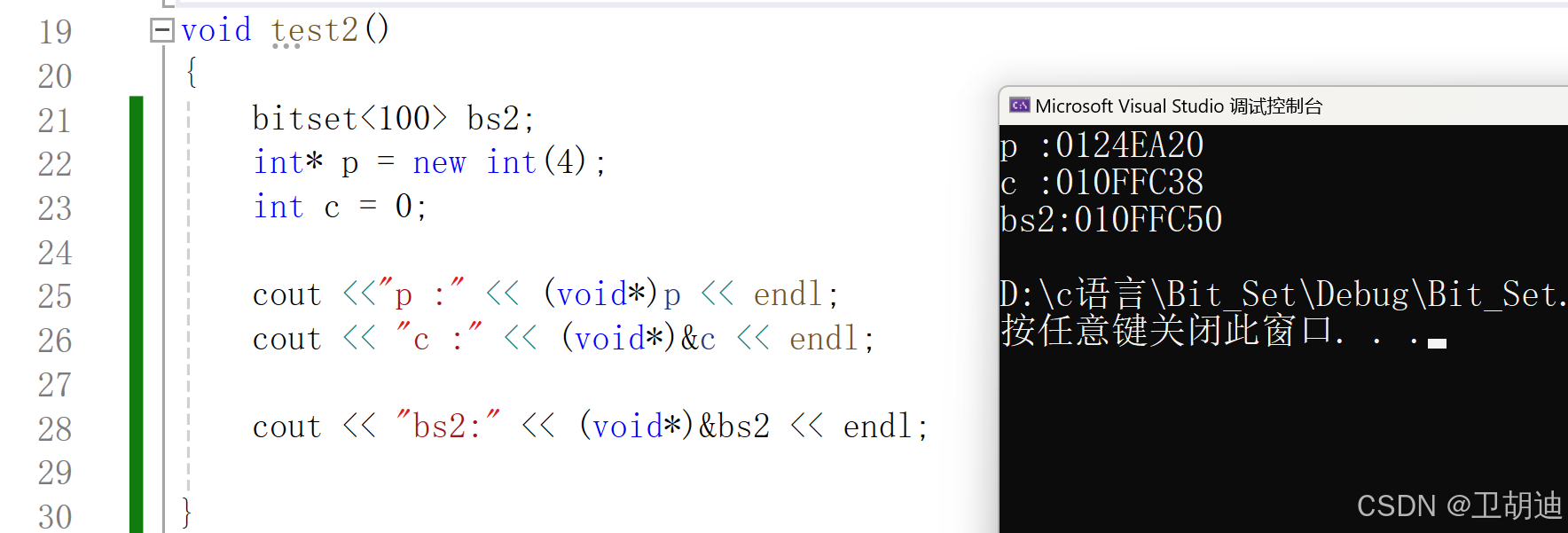
void test2()
{
bitset<100> bs2;
int* p = new int(4);
int c = 0;
cout <<"p :" << (void*)p << endl;
cout << "c :" << (void*)&c << endl;
cout << "bs2:" << (void*)&bs2 << endl;
}上述打印结果bs2的地址离栈区c位置近,离堆区p位置远,可以证明bitset在栈区开辟空间么?答案是否定的!!我们只能证明变量bs2存在栈区,但bs2里的内存不一定存在栈区,可能在bs2内部有个指针,指向真正存储的内存。
假如我们假设之前的bs1,如下图

我们可以发现变量bs1的确存储在栈区,但其内部有指针指向其他内存,所以之前打印的是帧数数据的地址,(void*)&bs1._bs[0] ,而不是bs1的地址。
对于自定义类型我们可以修改内部权限让我们访问真正内存的地址,但对于封装好的类,我们无法直接修改,只能通过其他手段验证。
有三个方面可以证明。
1.当我们开辟过大内存时,报错是栈溢出。

2.当我们开辟不同大小时,变量大小在变化

我们可以推测他底层与我们实现类似,20位要一个无符号整型,所以4个字节,100位要4个无符号整型,所以要16字节。
3.看内存
程序运行时在内存中查找bs1地址变化




内存的结果与我们预测一样,从而经过上述充分分析,我们可以断定STL就是在栈区开辟空间。
当然我们也有办法让他强制在堆区开辟内存,如下代码
void test3()
{
bitset<UINT_MAX>* p = new bitset<UINT_MAX>;
}

结果也是可以运行的。
总结
优点
1.访问效率高
2.占用内存少
缺点
1.只适用于整型,其他类型无法完美映射
代码
头文件
#pragma once
#include<iostream>
#include<vector>
using namespace std;
template<size_t N>
class bit_set
{
public:
bit_set()
{
//这里加一解决出现31/32=0或者32/32=1不足的情况
_bs.resize(N / 32 + 1);
}
//将对应位设置为1
bit_set& set(size_t x)
{
int i = x / 32;
int j = x % 32;
_bs[i] |= (1 << j);
return *this;
}
//将对应位设置为0
bit_set& reset(size_t x)
{
int i = x / 32;
int j = x % 32;
_bs[i] &= (~(1 << j));
return *this;
}
//当前位为1返回真否则返回假
bool test(size_t x) const
{
int i = x / 32;
int j = x % 32;
return _bs[i] & (1 << j);
}
size_t size()
{
return N;
}
//返回1的个数
size_t count()
{
size_t ret = 0;
for (int i = 0; i < N; i++)
{
if (test(i))
ret++;
}
return ret;
}
private:
vector<size_t> _bs;
};源文件
#include"Bit_Set.h"
#include<bitset>
void test1()
{
bit_set<100> bs;
int a[] = { 10,25,36,40,26 };#include"Bit_Set.h"
#include<bitset>
void test1()
{
bit_set<100> bs;
int a[] = { 10,25,36,40,26 };
for (int e : a)
bs.set(e);
for (int i = 0; i < 100; i++)
{
if(bs.test(i))
cout << i << " " << endl;
}
}
int main()
{
test1();
int a[] = { 5,6,3,8,4,9 };
return 0;
}
for (int e : a)
bs.set(e);
for (int i = 0; i < 100; i++)
{
if(bs.test(i))
cout << i << " " << endl;
}
}
int main()
{
test1();
int a[] = { 5,6,3,8,4,9 };
return 0;
}到这里就结束了,如果有错误欢迎在评论区指出。






























 152
152

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








